Skip to content
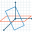
Чтобы найти поворот осей, зададим две системы координат, согласно рисунку
Пусть точка T в новой полярной системе координат имеет полярный радиус r и полярный угол φ. В старой полярной системе координат полярный угол точки T будет равен α+φ, а полярный радиус r будет как в новой системе координат.
Тогда уравнения примут вид:
x = r cos(α+φ)
y = r sin(α+φ)
Применяя тригонометрические тождества суммы двух углов для синуса и косинуса , получим выражения:
x = r (cosα cosφ — sinα sinφ) = r (cosφ) cosα — (r sinφ) sinα
y = r (sinα cosφ + cosα sinφ) = r (cosφ) sinα + (r sinφ) cosα
Обозначим
X = r cosφ и Y = r sinφ
Получим уравнения поворота осей координат
x = X cosα — Y sinα
y = X sinα + Y cosα
Если обозначим следующим образом
x = OK , y = KT — старые координаты точки T
x´= OK´, y´ = KT´ — новые координаты точки T
α — угол поворота осей
тогда формулы поворота осей координат примут вид:
Пример
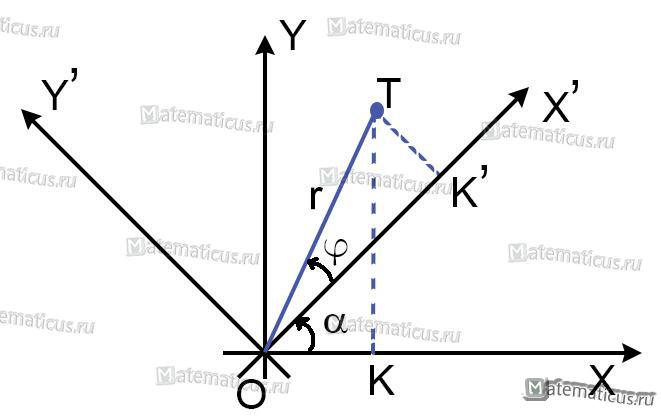
До поворота осей на угол -300 точка L имела абсциссу x=2 и ординату y=0
Требуется найти координаты точки L после поворота осей.
Решение
Подставляя в формулу, находим новые координаты осей x´, y´
12847
Исходим из уравнения
(1)
И покажем, что всегда можно выбрать угол поворота координатных осей так, что «смешанный» член
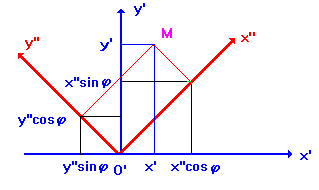
обратится в нуль. Пусть система координат X»O’y» получена поворотом системы X’O’y’ вокруг начала O’ на угол
.
Как видно из рисунка, «старые» и «новые» координаты связаны равенствами
(2)
Подставим их в уравнение (1)
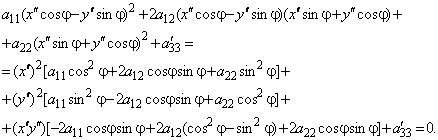
и выберем угол j так, чтобы она обращалась в нуль:
.
Разделим это уравнение на , получим
. Откуда найдем искомый угол
. (3)
Обозначая в (2) первые квадратные скобки , а вторые
, получим уравнение (20.4) в «новой» системе координат
. (4)
ВЫВОД: Для кривой, заданной уравнением (1), поворотом осей координат можно «уничтожить» смешанный (билинейный) член и преобразовать его к уравнению (4); при этом свободный член не изменяется.
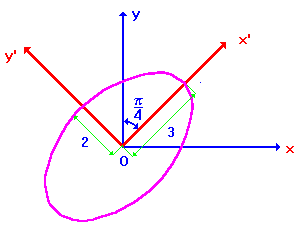
Пример 1. Поворотом осей координат установить тип кривой, заданной уравнением
.
Сравнивая с уравнением (20.4), находим
.
По формуле (3) найдем угол поворота .
Итак, для приведения кривой к каноническому виду следует сделать поворот осей на угол , при этом формулы перехода даются (2):
Подставим эти значения в исходное уравнение, получим
.
Разделим уравнение на свободный член и перенесем его в правую часть уравнения, получим — это эллипс с полуосями
.
| < Предыдущая | Следующая > |
|---|
Преобразования прямоугольных координат
Преобразование прямоугольных координат на плоскости
Получим формулы, связывающие координаты точки при переходе от одной прямоугольной системы координат к другой прямоугольной системе координат. Рассмотрим три типа преобразований:
а) параллельный перенос;
б) поворот системы координат;
в) зеркальное отражение в оси абсцисс (изменение направления оси ординат на противоположное).
В каждом случае координаты точки в старой и новой
системах координат связаны формулой (2.8). Поэтому достаточно найти вектор
переноса начала координат и матрицу
перехода от базиса
к базису
.
а) При параллельном переносе системы координат (рис.2.11,а) базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат:
. Тогда формулу (2.8) можно записать в виде
б) При повороте системы координат на угол (рис.2.11,6) начало
новой системы координат совпадает с началом
старой, поэтому вектор переноса нулевой:
. Разлагая новые базисные векторы
по старому базису, получаем
Составим матрицу перехода, записывая координаты векторов
по столбцам:
. Тогда формулу (2.8) можно записать в виде
в) При зеркальном отражении в оси абсцисс (изменении направления оси ординат на противоположное) (рис.2.11,в) начало новой системы координат совпадает с началом
старой, поэтому вектор переноса нулевой:
. Разлагая новые базисные векторы
по старому базису, получаем
(так как
),
или
. Составим матрицу перехода, записывая координаты векторов
по столбцам:
. Тогда формулу (2.8) можно записать в виде
.
Аналогично определяется зеркальное отражение в оси ординат (изменение направления оси абсцисс на противоположное).
Покажем, что любое преобразование прямоугольной системы координат сводится к последовательному применению рассмотренных преобразований, т.е. к композиции преобразований систем координат. Действительно, пусть на плоскости заданы две прямоугольные системы координат и
. Сначала, если точки
и
не совпадают, выполним параллельный перенос старой системы координат на вектор
, при этом получим систему координат
. Затем при помощи поворота на угол
совместим вектор
с вектором
, при этом получим систему координат
, где вектор
либо совпадает с вектором
, либо противоположен ему
. В первом случае, когда обе системы
и
одноименные, никаких преобразований делать уже не надо, так как полученная система координат
совпадает с заданной
(рис.2.12,а). Во втором случае, когда системы
и
разноименные, для получения системы
достаточно изменить направление оси ординат на противоположное, т.е. выполнить зеркальное отражение
в оси
(рис.2.12,6). Формулы, связывающие старые и новые координаты точки, имеют вид:
– при одноименных системах координат (рис.2.12,а):
(2.9)
– при разноименных системах координат (рис.2.12,6):
(2.10)
Таким образом, любое преобразование прямоугольной системы координат на плоскости сводится к композиции преобразований, каждое из которых является либо параллельным переносом, либо поворотом, либо зеркальным отражением в оси координат.
Замечания 2.3.
1. Для рассмотренных преобразований координат точек нетрудно получить выражения новых координат через старые:
Для преобразования (2.9) аналогичные формулы имеют вид:
2. При и
из соотношений (2.10) получается преобразование
изменяющее названия координатных осей (зеркальное отражение в прямой, содержащей биссектрису первого координатного угла).
3. Справедливо утверждение: любое преобразование прямоугольной системы координат на плоскости может быть представлено в виде композиции зеркальных отражений в некоторых прямых.
Для доказательства достаточно показать, что рассмотренные выше преобразования — параллельный перенос (рис.2.11,а) и поворот (рис.2.11,6) — можно представить при помощи композиции зеркальных отражений. Действительно, параллельный перенос системы координат вдоль оси абсцисс (на вектор ) можно получить при помощи двух отражений: первое — относительно оси ординат (получим систему координат
) , а второе — относительно прямой
, проходящей через точку
на оси абсцисс параллельно оси ординат (рис.2.13,а). Аналогично выполняется сдвиг вдоль оси ординат. Поэтому любой параллельный перенос сводится к композиции зеркальных отражений.
Чтобы получить поворот на угол , нужно выполнить два зеркальных отражения (рис.2.13,6): первое — относительно оси ординат (получим систему
), а второе — относительно биссектрисы
угла между векторами
и
.
4. Утверждение пункта 3 можно уточнить: любое преобразование прямоугольной системы координат на плоскости может быть представлено в виде композиции не более трех зеркальных отражений в некоторых прямых.
5. Преобразования координат (2.7) и (2.8) называются ортогональными, если матрица перехода ортогональная, т.е.
. Нетрудно но показать, что преобразования (2.9),(2.10) ортогональные, поэтому любое преобразование прямоугольной системы координат является ортогональным.
Пример 2.5. Известны координаты точек и
в прямоугольной системе координат
на плоскости. Найти координаты точки
в прямоугольной системе координат
, полученной при помощи зеркального отражения в некоторой прямой
системы
(рис.2.14).
Решение. Находим вектор переноса начала системы координат , его длину
и угол
между векторами
и
, так как
. Ось симметрии
при зеркальном отражении является серединным перпендикуляром к отрезку
, поэтому угол
, который образует ось симметрии с положительным направлением оси абсцисс
, равен
. Отражение в оси
представим в виде композиции следующих преобразований: параллельного переноса на вектор
; поворота на угол
; зеркального отражения в оси абсцисс (рис.2.12,6). Старые и новые координаты точки
связаны формулой (2.10) при
. Учитывая, что
и
получаем
Подставляя старые координаты точки
, получаем ее новые координаты:
Следовательно, точка имеет одинаковые координаты в обеих системах, т.е. точка
лежит на оси симметрии
.
Преобразования прямоугольных координат в пространстве
Получим формулы, связывающие координаты точки при переходе от одной прямоугольной системы координат в пространстве к другой прямоугольной системе координат.
Рассмотрим три типа преобразований прямоугольной системы координат:
а) параллельный перенос;
б) поворот вокруг координатной оси;
в) зеркальное отражение в координатной плоскости (изменение направления одной координатной оси на противоположное).
В каждом случае координаты точки в старой и новой
системах координат связаны формулой (2.7). Поэтому достаточно найти вектор
переноса начала координат и матрицу
перехода от базиса
к базису
.
а) При параллельном переносе системы координат базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат:
. Тогда формулу (2.7) можно записать в виде
б) При повороте системы координат на угол (рис.2.11,б) вокруг оси аппликат начало
новой системы координат совпадает с началом
старой, поэтому вектор переноса нулевой:
. Разлагая новые базисные векторы
по старому базису, получаем
Составим матрицу перехода , записывая координаты векторов
по столбцам. Тогда формулу (2.7) можно записать в виде
Очевидно, что система координат на плоскости при этом преобразовании поворачивается на угол
.
в) При зеркальном отражении в плоскости (изменении направления оси аппликат на противоположное) начало
новой системы координат совпадает с началом
старой, поэтому вектор переноса нулевой:
. Разлагая новые базисные векторы
по старому базису, получаем
Составим матрицу перехода
Тогда формулу (2.7) можно записать в виде
Аналогично определяются зеркальные отражения в других координатных плоскостях (изменение направлений осей абсцисс или ординат на противоположные).
Матрицы переходов в пунктах «а», «б» и «в» ортогональные (см. пункт 5 замечаний 2.3).
Как и в случае преобразований на плоскости, можно показать, что любое преобразование прямоугольной системы координат в пространстве сводится к композиции преобразований, каждое из которых является либо параллельным переносам, либо поворотам вокруг координатной оси, либо зеркальным отражением в координатной плоскости.
Углы Эйлера
Используя композицию, получим формулы преобразования координат точки в пространстве при переходе от старой прямоугольной системы к новой
, имеющей то же начало и ту же ориентацию (т.е. новая система координат получается из старой поворотом вокруг начала координат
). Обе системы координат изображены на рис.2.15 (полужирными и двойными линиями соответственно). Чтобы от системы
перейти к системе
нужно выполнить три поворота. Сначала проведем через точку
перпендикуляр
(линию узлов) к плоскости
. Направление на этом перпендикуляре выберем так, чтобы ориентация системы координат
совпадала бы с ориентацией системы координат
. Если оси
и
совпадают, то ось
выбирается совпадающей с осью
. Если оси
и
противоположно направлены, то и ось
выбирается противоположно направленной оси
. Затем последовательно сделаем три поворота:
– первый поворот выполним вокруг оси на угол
от оси
до оси
(получим систему координат
, оси
и
которой изображены штриховыми линиями на рис.2.15);
– второй поворот выполним вокруг оси на угол
от оси
до оси
, при этом ось
примет положение
(получим систему координат
, ось
которой Рис.2.15 изображена двойной штриховой линией на рис.2.15);
– третий поворот выполним вокруг оси на угол
от оси
до оси
.
Указанные углы называются углами Эйлера, в частности, угол
называется углом прецессии, угол
— углом нутации, а угол
— углом чистого вращения.
Согласно пункту «б», запишем матрицы переходов от базиса к базису для указанных поворотов соответственно:
По свойству 1 (см. разд.2.2.1) получаем матрицу перехода от базиса прямоугольной системы координат
к базису прямоугольной системы координат
:
Отсюда следуют формулы для преобразования прямоугольных координат точки
Поскольку каждая из матриц ортогональная, то и их произведение также является ортогональной матрицей (см. пункт 5 замечаний 2.3).
Пример 2.6. Прямоугольная система координат получена из стандартной системы координат
при помощи поворота на угол
вокруг прямой, проходящей через начало координат и образующей равные углы с координатными осями (на рис.2.16 эта прямая изображена одной точкой
, поскольку перпендикулярна плоскости рисунка). Требуется найти углы Эйлера.
Решение. Составим матрицу перехода от базиса
к базису
.
Так как , то
Сравнивая с матрицей , заключаем, что
(так как
и
);
(так как
и
);
(так как
и
).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
В
аналитической геометрии часто применяется
преобразование координат, называемое
поворотом
осей. Оно
заключается в следующем: обе оси координат
поворачиваются в одну сторону на один
и тот же угол, а начало координат остается
неизменным. Примеры использования этого
преобразования будут даны в следующих
двух параграфах.
Пусть
оси координат повернуты на угол
(рис. 3.14). Угол
– это угол, на который нужно повернуть
старую ось
до ее совмещения с новой осью
;
угол
считается положительным при повороте
против часовой стрелки.
Выведем
формулы, позволяющие выразить старые
координаты
и
любой точки
через ее новые координаты
и
.
Для
этого построим радиус-вектор
точки
и обозначим через
и
углы, образованные им соответственно
с осями
и
:
точка
имеет полярные координаты
и
,
если за полярную ось принять ось
,
и координаты
и
,
если за полярную ось принять ось
.
Углы
,
и
связаны равенством
.
Выражая декартовы координаты точки
через ее полярные координаты, имеем:
(А)
(Б)
Заменяя
в формулах (А)
на
и используя формулы для синуса и косинуса
суммы двух углов, находим:
,
.
Отсюда,
используя формулы (Б), находим следующие
формулы, выражающие старые координаты
и
через
новые координаты
и
:
(3.42)
,
.
Формулы обратного
перехода, выражающие новые координаты
через старые, мы получим аналогичным
путем из формул (Б), заменяя в них угол
на
:
(3.42′)
,
.
Формулы
(3.42′)
можно получить также из соотношений
(3.42), рассматривая их как уравнения,
определяющие
и
через
и
,
и разрешая их относительно
и
.
Формулы
(3.42′)
можно было бы получить из формул (3.42)
еще и следующим путем: поменять в формулах
(3.42) местами
и
,
а также
и
и заменить
на
(так как новые оси получаются из старых
поворотом на угол
,
то и старые оси могут быть получены из
новых поворотом в обратную сторону, т.
е. на угол
).
Рекомендуем
читателю получить формулы (3.42′)
этими двумя способами.
§ 3.9. Исследование общего уравнения кривой второго порядка Наиболее общее уравнение второй степени относительно и имеет вид:
(3.49)
.
В
аналитической геометрии его называют
общим уравнением кривой второго порядка.
От уравнения:
уравнение
(3.49) отличается наличием члена с
произведением координат, т. е. коэффициент
мы считаем не равным нулю.
В
настоящем параграфе наша задача –
показать, что и уравнение (3.49), так же,
как и уравнение (3.39), может определять
только одну из изученных нами ранее
кривых – эллипс, гиперболу или параболу
(с возможными для каждого из них случаями
вырождения), найти способ по виду
уравнения (3.49) установить тип определяемой
им кривой (подобно тому, как это делалось
для уравнения (3.39) по знаку произведения
)
и научиться для каждого конкретного
уравнения (3.49) строить кривую.
Наиболее
простой способ решения этой задачи –
при помощи поворота координатных осей
на некоторый угол
преобразовать уравнение (3.49) в уравнение
вида (3.39) по отношению к новой системе
координат, поскольку уравнение (3.39) нами
уже изучено во всех подробностях.
Итак,
повернем координатные оси на некоторый
угол
.
Новые оси координат обозначим через
и
.
Тогда старые координаты будут выражаться
через новые по формулам (3.42) так:
,
.
Подставляя
эти значения
и
в уравнение (3.49), после приведения
подобных членов приведем его к виду:
(3.50)
Уравнение (3.50) имеет
ту же структуру, что и уравнение (3.49).
его можно записать в виде:
(3.50′)
где
(3.51)
(Значения
новых коэффициентов
и
,
несущественные для дальнейшего, мы не
описываем.)
Выберем
теперь угол
таким, чтобы новый коэффициент
в уравнении (3.50′)
обратился бы в нуль; это дает нам для
определения угла
уравнение:
(3.52)
,
откуда
находим:
(3.53)
.
Формула
(3.53) определяет два значения угла
,
разность между которыми равна
;
поэтому безразлично, какое из них
выбрать: переход от одного к другому
равносилен перестановке новых осей
координат
и
.
После
того, как угол
определен по формуле (3.53), уравнение
(3.50′)
приводится к виду:
(3.54)
и,
как нам известно, определяет эллипс
(окружность), гиперболу или параболу
(или вырождения этих кривых) в зависимости
от знака произведения
(см. § 3.6.).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
-
Линейная алгебра
Расчёт углов поворота между двумя системами координат
Есть ортогональная трёхмерная система координат (OXYZ). Есть другая ортогональная система координат (OX`Y`Z`), повёрнутая относительно первой на неизвестные углы. Центры систем координат совпадают. В системе координат (OXYZ) мы знаем координаты вектора OX` и вектора OZ`. Необходимо найти матрицу поворота для перехода из системы координат (OXYZ) в (OX`Y`Z`). Помогайте, а то весь мозг себе сломал. Или подскажите в какую сторону копать.
-
Вопрос заданболее трёх лет назад
-
22403 просмотра
1
комментарий
-
Столкнулся с очень похожей проблемой. Вопрос автору. Так какое же решение подошло наилучшим образом?
Решения вопроса 1
ОМГ, в шоке от ответов про кватернионы ))
Если координаты в XYZ
OX’ = (x1, y1, z1)
OY’ = (x2, y2, z2)
OZ’ = (x3, y3, z3)
То матрица преобразования из XYZ в X`Y`Z`
x1, x2, x3
y1, y2, y3
z1, z2, z3
Собственно практически по определению
-
Максим
@R6MF49T2 Автор вопроса
Всё же получится матрица преобразования из X`Y`Z` в XYZ. Но по условию задачи известны координаты только осей OX’ и OZ’. Координаты OY’ не известны.
-
Максим
@R6MF49T2 Автор вопроса
Но всё равно спаибо, можно попробовать посчитать координаты третей оси, так как решение с поворотами до совмещение осей дало громадную результирующую матрицу поворота.
-
координаты 3-й оси — это векторное произведение первых двух
Пригласить эксперта
Ответы на вопрос 5
Извините, если я сейчас ошибаюсь, но у вас будет две матрицы поворота. Вокруг оси X и вокруг оси Y. Вот они:
Вокруг X:
Вокруг Y:
Ну, а найти углы поворотов это элементарно:
Ведь у вас есть координаты OX` и OY` в исходной системе.
-
Максим
@R6MF49T2 Автор вопроса
по идее если по матрице перехода пересчитать допустим ось OX то она должна совпасть с осью OX’. как это сделать без поворота вокруг оси OZ я не представляю. В моём понимании должно быть как минимум 3 поворота.
-
Поворот по двум осям задает угол поворота по третей единственным образом.
-
Максим
@R6MF49T2 Автор вопроса
Хорошо, вот только не понял углы поворота фи и пси между чем и чем? Лично мне их найти не так элементарно как вам и я не понимаю что за формулу вы дали.
-
Угол фи, это угол между векторами OX и OX`, угол пси это угол между OY и OY`. Что бы их найти нужно подставить соответствующие векторы в формулу и вычислить арккосинус от того, что получится.
-
Максим
@R6MF49T2 Автор вопроса
теперь понятно. Вот только всё же в первом сообщении вы пишете о повороте вокруг оси X и Y. А если угол фи это угол между векторами OX и OX` то вращать нам надо всё же вокруг OY’ для совмещения OX и OX`. Обозначим эту новую повёрнутую систему как OX«Y»Z». для совмещения осей OY и OY» расчитываем угол между ними и поворачиваем вокруг оси OX», она же OX’. Так?
-
Максим
@R6MF49T2 Автор вопроса
Что такое кватернион я знаю. Проблема здесь не выполнить поворот, а определить оси вращения и углы на которые нужно выполнять поворот.
-
Поворачиваем систему координат сперва так, чтобы совпал OX’ с OX, при этом OY’ переходит в, скажем, OY». Потом повернутую систему поворачиваем второй раз (вокруг OX’) чтобы OY» совпал с OY. (При первом повороте ось вращения получим как векторное произведение OX’ и OX, а угол поворота — в обоих случаях — через скалярное, формулу уже привели выше.) Оба поворота выразим кватернионами, и потом из их композиции и получим и ось, и угол.
-
Максим
@R6MF49T2 Автор вопроса
так как мы рассчитываем переход из системы OXYZ к OX’Y’Z’ то соответственно предлагаю доворачивать OXYZ до OX’Y’Z’ а не наоборот. Итак вначале по формуле
рассчитываем угол между OX и OX’ и поворочиваетм по оси OY’. при этом у нас совпадут OX’ и OX Повёрнутую систему обзовём OX«Y»Z». Теперь чтобы совместить OY’ и OY» находим между ними угол и поворачиваем вдоль оси OX», он же OX’. Так?
-
Да, верно — второй поворот делать вокруг того вектора, который уже совмещен. Но чтобы совместить его первым поворотом, векторное произведение посчитать, в общем случае, всё же нужно. И использовать это векторное произведение как ось вращения для первого поворота. Разве что, по условиям задачи, OY’ — это нормаль к плоскости XOX’?
P.S.: Случайно изменил обозначения по сравнению с теми, что были в вопросе. В вопросе — векторы OX’ и OZ’, а у меня — OX’ и OY’.
Насколько я могу припомнить, если мы возьмём координаты ортов новой системы, помещённых в старую, то эти координаты и будут строками искомой матрицы.
-
Максим
@R6MF49T2 Автор вопроса
Точно строками? Предположим что новая система координат отличается от старой только поворотом вокруг оси y на 45 градусов. тогда если верить вашим словам матрица поворота примет вид:
0.7, 0, 0.7
0, 0, 0
-0.7, 0, 0.7умножим на эту матрицу вектор OX
1
0
0и получим вектор с координатами 0.7, 0, -0.7. А должны были 0.7, 0, 0.7.
-
Значит, столбцами — зависит от формы записи. Мне приходилось иметь дело с обоими вариантами, так что сразу не сориентировался, что требуется для классического варианта. Кстати, второй вектор будет всё же (0, 1, 0).
@VoidVolker
Разработчик ПО и IT-инженер
Похожие вопросы
-
Показать ещё
Загружается…
28 мая 2023, в 08:16
5000 руб./за проект
28 мая 2023, в 07:29
1500 руб./за проект
28 мая 2023, в 02:05
7000 руб./за проект


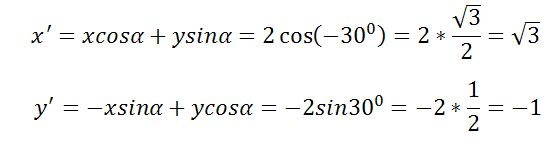
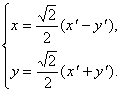
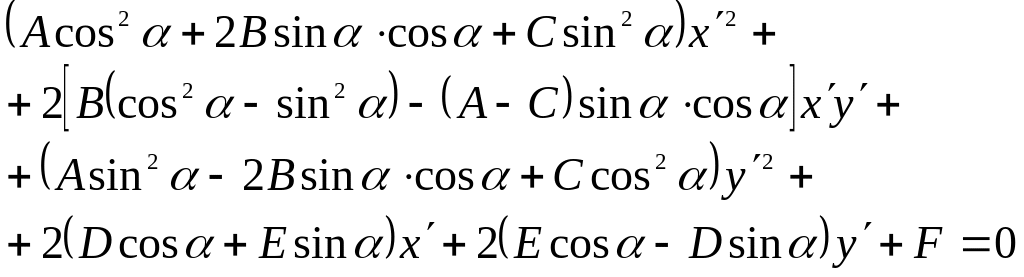


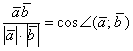
 рассчитываем угол между OX и OX’ и поворочиваетм по оси OY’. при этом у нас совпадут OX’ и OX Повёрнутую систему обзовём OX«Y»Z». Теперь чтобы совместить OY’ и OY» находим между ними угол и поворачиваем вдоль оси OX», он же OX’. Так?
рассчитываем угол между OX и OX’ и поворочиваетм по оси OY’. при этом у нас совпадут OX’ и OX Повёрнутую систему обзовём OX«Y»Z». Теперь чтобы совместить OY’ и OY» находим между ними угол и поворачиваем вдоль оси OX», он же OX’. Так?