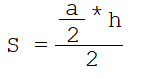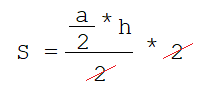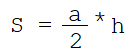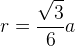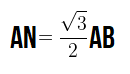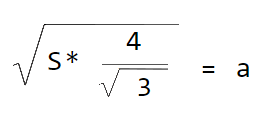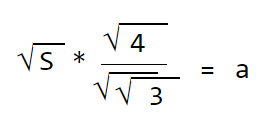From Wikipedia, the free encyclopedia
| Equilateral triangle | |
|---|---|
 |
|
| Type | Regular polygon |
| Edges and vertices | 3 |
| Schläfli symbol | {3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | D3 |
| Area |  |
| Internal angle (degrees) | 60° |
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
Principal properties[edit]
An equilateral triangle. It has equal sides (


Denoting the common length of the sides of the equilateral triangle as 
Denoting the radius of the circumscribed circle as R, we can determine using trigonometry that:
- The area of the triangle is
Many of these quantities have simple relationships to the altitude («h») of each vertex from the opposite side:
In an equilateral triangle, the altitudes, the angle bisectors, the perpendicular bisectors, and the medians to each side coincide.
Characterizations[edit]
A triangle 













Sides[edit]
Semiperimeter[edit]
Angles[edit]
Area[edit]
Circumradius, inradius, and exradii[edit]
Equal cevians[edit]
Three kinds of cevians coincide, and are equal, for (and only for) equilateral triangles:[7]
- The three altitudes have equal lengths.
- The three medians have equal lengths.
- The three angle bisectors have equal lengths.
Coincident triangle centers[edit]
Every triangle center of an equilateral triangle coincides with its centroid, which implies that the equilateral triangle is the only triangle with no Euler line connecting some of the centers. For some pairs of triangle centers, the fact that they coincide is enough to ensure that the triangle is equilateral. In particular:
- A triangle is equilateral if any two of the circumcenter, incenter, centroid, or orthocenter coincide.[8]: p.37
- It is also equilateral if its circumcenter coincides with the Nagel point, or if its incenter coincides with its nine-point center.[6]
Six triangles formed by partitioning by the medians[edit]
For any triangle, the three medians partition the triangle into six smaller triangles.
- A triangle is equilateral if and only if any three of the smaller triangles have either the same perimeter or the same inradius.[9]: Theorem 1
- A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the same distance from the centroid.[9]: Corollary 7
Points in the plane[edit]
Notable theorems[edit]
Visual proof of Viviani’s theorem
Morley’s trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle.
Napoleon’s theorem states that, if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, the centers of those equilateral triangles themselves form an equilateral triangle.
A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral.[11]
Viviani’s theorem states that, for any interior point 




independent of the location of 
Pompeiu’s theorem states that, if 








Geometric construction[edit]
Construction of equilateral triangle with compass and straightedge
An equilateral triangle is easily constructed using a straightedge and compass, because 3 is a Fermat prime. Draw a straight line, and place the point of the compass on one end of the line, and swing an arc from that point to the other point of the line segment. Repeat with the other side of the line. Finally, connect the point where the two arcs intersect with each end of the line segment
An alternative method is to draw a circle with radius 
In both methods a by-product is the formation of vesica piscis.
The proof that the resulting figure is an equilateral triangle is the first proposition in Book I of Euclid’s Elements.
Derivation of area formula[edit]
The area formula 

Using the Pythagorean theorem[edit]
The area of a triangle is half of one side 

An equilateral triangle with a side of 2 has a height of √3, as the sine of 60° is √3/2.
The legs of either right triangle formed by an altitude of the equilateral triangle are half of the base 

so that
Substituting 

Using trigonometry[edit]
Using trigonometry, the area of a triangle with any two sides 


Each angle of an equilateral triangle is 60°, so
The sine of 60° is 
since all sides of an equilateral triangle are equal.
Other properties[edit]
An equilateral triangle is the most symmetrical triangle, having 3 lines of reflection and rotational symmetry of order 3 about its center, whose symmetry group is the dihedral group of order 6, 
By Euler’s inequality, the equilateral triangle has the smallest ratio of the circumradius 

Given a point 








For any point 






For any point 



where 


For any point 



For any point 







Moreover, if point 








which also equals 

which is the optic equation.
For an equilateral triangle:
- The ratio of its area to the area of the incircle,
, is the largest of any triangle.[21]: Theorem 4.1
- The ratio of its area to the square of its perimeter,
is larger than that of any non-equilateral triangle.[11]
If a triangle is placed in the complex plane with complex vertices 



The equilateral triangle tiling fills the plane.
Notably, the equilateral triangle tiles two dimensional space with six triangles meeting at a vertex, whose dual tessellation is the hexagonal tiling. 3.122, 3.4.6.4, (3.6)2, 32.4.3.4, and 34.6 are all semi-regular tessellations constructed with equilateral triangles.[23]
A regular tetrahedron is made of four equilateral triangles.
In three dimensions, equilateral triangles form faces of regular and uniform polyhedra. Three of the five Platonic solids are composed of equilateral triangles: the tetrahedron, octahedron and icosahedron.[24]: p.238 In particular, the tetrahedron, which has four equilateral triangles for faces, can be considered the three-dimensional analogue of the triangle. All Platonic solids can inscribe tetrahedra, as well as be inscribed inside tetrahedra. Equilateral triangles also form uniform antiprisms as well as uniform star antiprisms in three-dimensional space. For antiprisms, two (non-mirrored) parallel copies of regular polygons are connected by alternating bands of 
As a generalization, the equilateral triangle belongs to the infinite family of 

In culture and society[edit]
Equilateral triangles have frequently appeared in man made constructions:
- The shape occurs in modern architecture such as the cross-section of the Gateway Arch.[29]
- Its applications in flags and heraldry includes the flag of Nicaragua[30] and the flag of the Philippines.[31]
- It is a shape of a variety of road signs, including the yield sign.[32]
See also[edit]
- Almost-equilateral Heronian triangle
- Isosceles triangle
- Ternary plot
- Trilinear coordinates
References[edit]
- ^ Bencze, Mihály; Wu, Hui-Hua; Wu, Shan-He (2008). «An equivalent form of fundamental triangle inequality and its applications» (PDF). Journal of Inequalities in Pure and Applied Mathematics. 10 (1): 1–6 (Article No. 16). ISSN 1443-5756. MR 2491926. S2CID 115305257. Zbl 1163.26316.
- ^ Dospinescu, G.; Lascu, M.; Pohoata, C.; Letiva, M. (2008). «An elementary proof of Blundon’s inequality» (PDF). Journal of Inequalities in Pure and Applied Mathematics. 9 (4): 1-3 (Paper No. 100). ISSN 1443-5756. S2CID 123965364. Zbl 1162.51305.
- ^ Blundon, W. J. (1963). «On Certain Polynomials Associated with the Triangle». Mathematics Magazine. Taylor & Francis. 36 (4): 247–248. doi:10.2307/2687913. JSTOR 2687913. S2CID 124726536. Zbl 0116.12902.
- ^ a b Alsina, Claudi; Nelsen, Roger B. (2009). When less is more. Visualizing basic inequalities. Dolciani Mathematical Expositions. Vol. 36. Washington, D.C.: Mathematical Association of America. pp. 71, 155. doi:10.5948/upo9781614442028. ISBN 978-0-88385-342-9. MR 2498836. OCLC 775429168. S2CID 117769827. Zbl 1163.00008.
- ^ a b Pohoata, Cosmin (2010). «A new proof of Euler’s inradius — circumradius inequality» (PDF). Gazeta Matematica Seria B (3): 121–123. S2CID 124244932.
- ^ a b c Andreescu, Titu; Andrica, Dorian (2006). Complex Numbers from A to…Z (1st ed.). Boston, MA: Birkhäuser. pp. 70, 113–115. doi:10.1007/0-8176-4449-0. ISBN 978-0-8176-4449-9. OCLC 871539199. S2CID 118951675.
- ^ Owen, Byer; Felix, Lazebnik; Deirdre, Smeltzer (2010). Methods for Euclidean Geometry. Classroom Resource Materials. Vol. 37. Washington, D.C.: Mathematical Association of America. pp. 36, 39. doi:10.5860/choice.48-3331. ISBN 9780883857632. OCLC 501976971. S2CID 118179744.
- ^ Yiu, Paul (1998). «Notes on Euclidean Geometry» (PDF). Florida Atlantic University, Department of Mathematical Sciences (Course Notes).
- ^ a b Cerin, Zvonko (2004). «The vertex-midpoint-centroid triangles» (PDF). Forum Geometricorum. 4: 97–109.
- ^ a b «Inequalities proposed in «Crux Mathematicorum»» (PDF).
- ^ a b Chakerian, G. D. «A Distorted View of Geometry.» Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ^ a b c Posamentier, Alfred S.; Salkind, Charles T. (1996). Challenging Problems in Geometry. Dover Publ.
- ^ Conway, J. H., and Guy, R. K., «The only rational triangle», in The Book of Numbers, 1996, Springer-Verlag, pp. 201 and 228–239.
- ^ Leon Bankoff and Jack Garfunkel, «The heptagonal triangle», Mathematics Magazine 46 (1), January 1973, 7–19,
- ^ Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics. Dover Publ. pp. 379–380.
- ^ Svrtan, Dragutin; Veljan, Darko (2012). «Non-Euclidean versions of some classical triangle inequalities» (PDF). Forum Geometricorum. 12: 197–209.
- ^ Lee, Hojoo (2001). «Another proof of the Erdős–Mordell Theorem» (PDF). Forum Geometricorum. 1: 7–8.
- ^ Gardner, Martin, «Elegant Triangles», in the book Mathematical Circus, 1979, p. 65.
- ^ Meskhishvili, Mamuka (2021). «Cyclic Averages of Regular Polygonal Distances» (PDF). International Journal of Geometry. 10: 58–65.
- ^ De, Prithwijit (2008). «Curious properties of the circumcircle and incircle of an equilateral triangle» (PDF). Mathematical Spectrum. 41 (1): 32–35.
- ^ Minda, D.; Phelps, S. (2008). «Triangles, ellipses, and cubic polynomials». American Mathematical Monthly. 115 (October): 679–689. doi:10.1080/00029890.2008.11920581. JSTOR 27642581. S2CID 15049234.
- ^ Dao, Thanh Oai (2015). «Equilateral triangles and Kiepert perspectors in complex numbers» (PDF). Forum Geometricorum. 15: 105–114.
- ^ Grünbaum, Branko; Shepard, Geoffrey (November 1977). «Tilings by Regular Polygons» (PDF). Mathematics Magazine. Taylor & Francis, Ltd. 50 (5): 231–234. doi:10.2307/2689529. JSTOR 2689529. MR 1567647. S2CID 123776612. Zbl 0385.51006.
- ^ a b Johnson, Norman W. (2018). Geometries and Transformations (1st ed.). Cambridge: Cambridge University Press. pp. xv, 1–438. doi:10.1017/9781316216477. ISBN 978-1107103405. S2CID 125948074. Zbl 1396.51001.
- ^ Cromwell, Peter T. (1997). «Chapter 2: The Archimedian solids». Polyhedra (1st ed.). New York: Cambridge University Press. p. 85. ISBN 978-0521664059. MR 1458063. OCLC 41212721. Zbl 0888.52012.
- ^ Klitzing, Richard. «n-antiprism with winding number d». Polytopes & their Incidence Matrices. bendwavy.org (Anton Sherwood). Retrieved 2023-03-09.
- ^ Webb, Robert. «Stella Polyhedral Glossary». Stella. Retrieved 2023-03-09.
- ^ H. S. M. Coxeter (1948). Regular Polytopes (1 ed.). London: Methuen & Co. LTD. pp. 120–121. OCLC 4766401. Zbl 0031.06502.
- ^ Pelkonen, Eeva-Liisa; Albrecht, Donald, eds. (2006). Eero Saarinen: Shaping the Future. Yale University Press. pp. 160, 224, 226. ISBN 978-0972488129.
- ^ White, Steven F.; Calderón, Esthela (2008). Culture and Customs of Nicaragua. Greenwood Press. p. 3. ISBN 978-0313339943.
- ^ Guillermo, Artemio R. (2012). Historical Dictionary of the Philippines. Scarecrow Press. p. 161. ISBN 978-0810872462.
- ^ Riley, Michael W.; Cochran, David J.; Ballard, John L. (December 1982). «An Investigation of Preferred Shapes for Warning Labels». Human Factors: The Journal of the Human Factors and Ergonomics Society. 24 (6): 737–742. doi:10.1177/001872088202400610. S2CID 109362577.
External links[edit]
- Weisstein, Eric W. «Equilateral Triangle». MathWorld.
Fundamental convex regular and uniform polytopes in dimensions 2–10 |
|||||
|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |
Правильный треугольник

4.6
Средняя оценка: 4.6
Всего получено оценок: 117.
4.6
Средняя оценка: 4.6
Всего получено оценок: 117.
Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.
Опыт работы учителем математики — более 33 лет.
Определение
Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.
Формулы правильного треугольника
Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.
Площадь
Начнем с формулы площади.
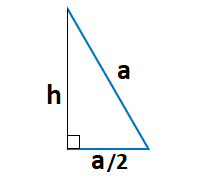
Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.
В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
$$Sin(ВАM)={ВMover AB}$$
С другой стороны синус 60 градусов заранее известнее и равен $sqrt{3} over 2$ . Значит можно выразить значение АМ:
$$ВМ=АВ*sin(ВАM)=AB* {sqrt{3}over 2}$$
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
AB=AC=BC=a
Тогда формула будет выглядеть следующим образом:
$$ВМ=а*{sqrt{3}over2}$$
Теперь вспомним классическую формулу площади треугольника:
$S= {1over2}h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:
$$S={1over2}*АC*ВM={1over2}*a*a*{sqrt{3}over2}=a^2*{sqrt{3}over4}$$
Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади через значение одной стороны.
Периметр
Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:
Р=3а
Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.
В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.
Что мы узнали?
Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
-
Иван Дарьин
5/5
-
Василий Головин
5/5
-
Денис Каспер
5/5
Оценка статьи
4.6
Средняя оценка: 4.6
Всего получено оценок: 117.
А какая ваша оценка?
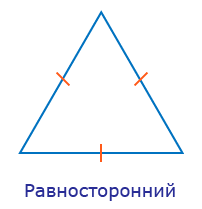
Равносторонний треугольник
Если три стороны треугольника имеют одинаковую длину, то треугольник является равносторонним.
Свойства равностороннего треугольника:
- 1) все стороны равны;
- 2) углы каждого равностороннего треугольника равны (60°);
- 3) каждая высота также является медианой и биссектрисой и они равны между собой;
- 4) каждая медиана является также высотой и биссектрисой;
- 5) каждая биссектриса является высотой и медианой;
- 6) точка пересечения высот, биссектрис и медиан разделяется в отношении 2:1;
- 7) площадь равностороннего треугольника:
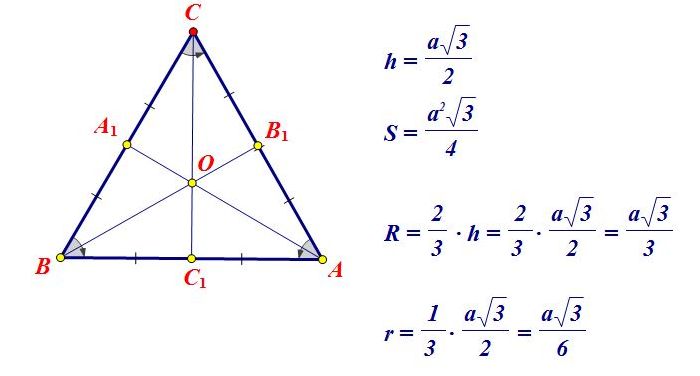
(frac{a^2√3}{4})
-
высоты, медианы и биссектрисы равностороннего треугольника равны:
(frac{a√3}{2});
- 9) Радиус описанной окружности (R) :
(frac{a√3}{3}) или (frac{a}{√3})
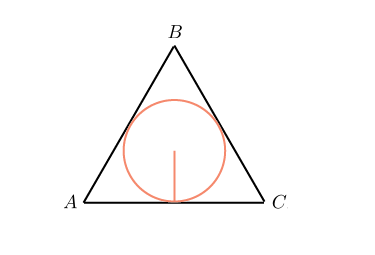
- 10) Радиус вписанной окружности (r) :
(frac{a}{2√3}) или (frac{a√3}{6})
где (a) — сторона треугольника.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
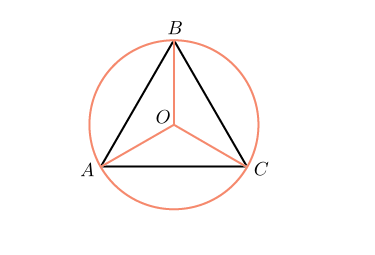
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
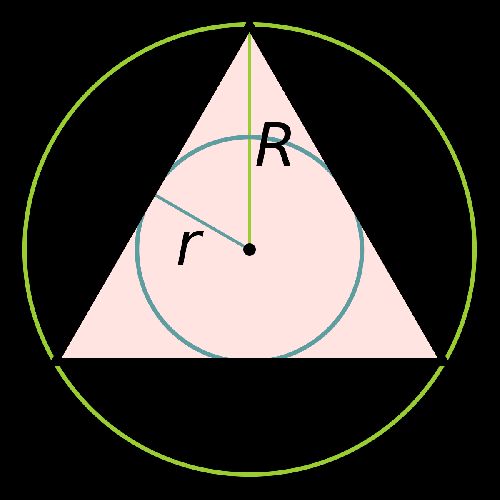
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Правильный треугольник

Средняя оценка: 4.6
Всего получено оценок: 80.
Средняя оценка: 4.6
Всего получено оценок: 80.
Правильный треугольник имеет много специфических свойств, которые значительно упрощают решение задач. Поэтому имеет смысл поговорить о каждом из этих свойств, дабы облегчить решение задач.
Определение
Правильный треугольник – это треугольник, у которого все стороны равны и каждый угол равен 60 градусам. Правильный треугольник еще называют равносторонним. О формулах правильного треугольника, и о том, как производить по ним различные вычисления – поговорим ниже.
Формулы правильного треугольника
Почти все формулы вытекают из утверждения о том, что правильный треугольник имеет 3 угла по 60 градусов и 3 одинаковые стороны.
Площадь
Начнем с формулы площади.
Равносторонний треугольник любой высотой делится на два, равных между собой прямоугольных треугольника. Теперь найдем значение высоты, подставим его в классическую формулу площади треугольника и получим формулу для нахождения площади правильного треугольника.
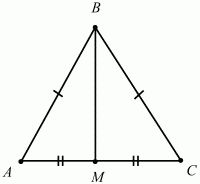
В прямоугольном треугольнике АВМ катет ВМ можно выразить через синус угла ВАМ. Этот угол известен и равен 60 градусам, значит, известны и значения синуса и косинуса для этого угла. Катет ВМ противолежащий, значит, для его нахождения необходимо воспользоваться формулой синуса.
С другой стороны синус 60 градусов заранее известнее и равен $sqrt <3>over 2$ . Значит можно выразить значение АМ:
Все стороны треугольника между собой равны, поэтому для удобства обозначим их через букву а.
Тогда формула будет выглядеть следующим образом:
Теперь вспомним классическую формулу площади треугольника:
$S= <1over2>h*a$, где а это основание треугольника, h – высота, проведенная к этому основанию. В заданном треугольнике это будет выглядеть следующим образом:
Получившаяся формула гораздо проще классических в плане количества необходимых параметров. Для нахождения площади правильного треугольника необходимо знать только значение одной из его сторон. Это возможно за счет равенства углов в таком треугольнике.
Только в правильном треугольнике возможно нахождение площади через значение одной стороны.
Периметр
Периметр найти ещё проще, так как это сумма всех сторон треугольника, а они все равны между собой, то:
Подобный подход, где приравниваются стороны или используются свойства медиан и биссектрис равностороннего треугольника, часто используется при решении подобных задач. У правильного треугольника нет и не может объема, так как это плоская фигура. У нее два характеризующих понятия: площадь и периметр.
В равностороннем треугольнике каждая биссектриса совпадает с медианой и высотой. Также совпадают и точки пересечения этих отрезков. Получившаяся точка зовется центром фигуры.
Что мы узнали?
Из статьи мы узнали, что у правильного треугольника все стороны и углы равны между собой. Мы узнали о свойствах биссектрисы, медианы и высоты – в правильном треугольнике это будет одна и та же линия. Ее можно проводить от любой вершины.
Правильный треугольник. Площадь правильного треугольника
Правильный треугольник — треугольник, у которого все стороны равны. Каждый угол правильного треугольника равен градусов.
Правильный треугольник называют еще равносторонним.
Каждая из высот правильного треугольника является также его медианой и биссектрисой.
Центры вписанной и описанной окружностей правильного треугольника совпадают.
Пусть сторона правильного треугольника равна .
Высота правильного треугольника:
Радиус окружности, вписанной в правильный треугольник: .
Радиус описанной окружности в два раза больше: .
Площадь правильного треугольника: .
Все эти формулы легко доказать. Если вы нацелены на решение задач части — докажите их самостоятельно.
. Сторона правильного треугольника равна . Найдите радиус окружности, вписанной в этот треугольник.
Задача решается в одну строчку. Радиус вписанной окружности .
. Найдите радиус окружности, вписанной в правильный треугольник, высота которого равна .
Сравним формулы для высоты правильного треугольника и радиуса вписанной окружности. Очевидно, радиус вписанной окружности равен высоты.
. Сторона правильного треугольника равна . Найдите радиус окружности, описанной около этого треугольника.
Радиус окружности, описанной вокруг правильного треугольника, равен .
http://obrazovaka.ru/geometriya/pravilnyy-treugolnik-formuly.html
http://ege-study.ru/ru/ege/materialy/matematika/pravilnyj-treugolnik-i-ego-ploshhad/
Что такое равносторонний треугольник, площадь равносторонних треугольников, равносторонние треугольники примеры.
Если все углы треугольника равны то, то это равносторонний треугольник и все стороны у такого треугольника равны.
Что такое равносторонний треугольник
В равностороннем треугольнике все углы равны аксиома.
На странице виды треугольников, мы упоминали о таком виде треугольников, как равносторонний треугольник.
Что из себя представляет равносторонний треугольник!?
Из самого названия видно, что все стороны данного треугольника равны:
Равносторонний треугольник называют еще правильным.
Какой первый интересный вопрос у вас возникает при виде равностороннего треугольника!?
Сколько градусов составляет угол в равностороннем треугольнике!?
Нет!? Не угадал… жаль…
смайлы
Но тем не менее, раз уж вопрос задан, то узнать сколько градусов составляет угол разностороннего треугольника :
180° разделить на 3…
180°/3 = 60°
Поскольку у нас треугольник равносторонний. то все углы у такого треугольника будут равны…
Равносторонний треугольник максимальный угол
Поисковый запрос -> «равносторонний треугольник максимальный угол» — не может быть максимальный, минимальный угол в равностороннем треугольнике — потому, что угол в равностороннем треугольнике всегда один!
60°
Высота равностороннего треугольника
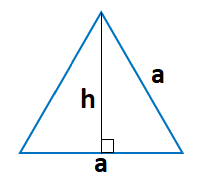
Формула высоты равностороннего треугольника, если сторону выразить через символ «a», то формула звучит так :
Высота равностороннего треугольника равна , корень из 3 деленное на 2 и умножить на сторону равностороннего квадрата.
Высота равностороннего треугольника формула через сторону
Доказательство :
Докажем что высота равностороннего треугольника равна — корню из 3, умноженное на сторону и деленное на 2.
Если мы опустим высоту из верхнего угла, то это будет биссектрисой, которая в данном случае не только разделит угол пополам, но и сторону противолежащую…
И если верхний угол будет поделен на 2, то он будет равен :
60 / 2 = 30
И если мы прибавим 30 и например оставшийся справа 60, то получим 60 + 30 = 90.
И далее мы можем получить угол между высотой «h» и стороной «a».
180 — 90 = 90
И мы получим прямоугольный треугольник, в котором все стороны обозначены…
…и отсюда мы уже можем вывести по теореме пифагора
c² = a² + b²
a² = a²2² + h² = a²4 + h²
Обе стороны умножим на 4, чтобы избавиться от 4 в дроби :
4a² = a² + 4h²
высоту оставляем одну слева и получаем:
4a² — a² = 4h² -> 4h² = 4a² — a² -> 4h² = 3a² -> h² = 3a²/4
И осталось извлечь квадратный корень из правой стороны…
h = √3a²/4
И далее получаем 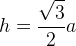
Площадь равностороннего треугольника
Какая формула для площади равностороннего треугольника!?
Она звучит так:
Площадь равностороннего треугольника равна : корень из 3 деленное на 4, умноженное на сторону в квадрате:
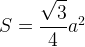
Доказательство :
Доказательство очень простое !
Выше мы уже доказали, чему равна высота… возьмем одну сторону треугольника на высоту h.
Вторая сторона будет равна а/2
И далее нам нужно умножить высоту на сторону, поделив на 2. По правилу вычисления площади прямоугольного треугольника.
Мы получаем предварительный результат:
И поскольку у нас два таких треугольника, то правую сторону надо умножить на 2, две двойки сокращаются.
получаем :
И далее заменим высоту из выше пройденного пункта:
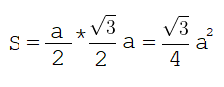
Радиус окружности, вписанной в равносторонний треугольник
Или вам может встретиться вторая формула вписанной окружности в равносторонний треугольник :
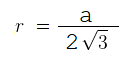
Почему встречаются две формулы радиуса вписанной окружности!?
Потому, что они выводятся разными путями, хоть они и не похожи — но это одинаковые значения.
Сможете доказать самостоятельно выше озвученный тезис?
Доказательство первой формулы радиус вписанной окружности равностороннего треугольника
Соотношение радиуса вписанной и описанной окружностей 1 : 2(на момент написания данной страницу мы еще это не прошли на сайте)
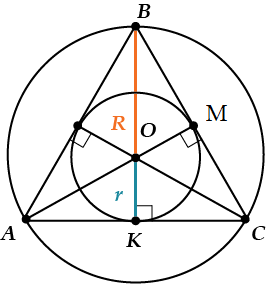
Отсюда мы получаем, что :
r =13 * h
Подставляем ранее выведенную высоту
r =13 * √32a =
√36a
Доказательство второй формулы радиус вписанной окружности равностороннего треугольника
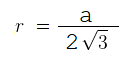
Не будем здесь доказывать, что два треугольника «ABM» и «AOK» подобные и отличаются в своих размерах и других показателях на коэффициент «Х».
Из этого мы можем создать зависимость:
«r» — относится к отрезку «AK», как «BM» к «AM»
«AK» и «BM» равны одному и тому же а/2.
«AM» — это у нас высота — «h».
Далее мы можем записать эту зависимость как :
r : а2 =
а2 : h
Как вы знаете, что при делении подобные выражения ведут себя не так, как при умножении(скоро и про это напишем), поэтому заменим деление на умножение:
r * 2а =
а2 * 1h
Теперь мы можем избавиться в левой стороне от дроби 2/а, умножив две стороны на а/2 :
r = а2 * а2 * 1h
В последней дроби заменяем «h» на наши значение из пункта 2 и поскольку получается опять деление, меняем знак и переворачиваем дробь( см.: деление дробей)
r = а2 * а2 * 1h =
а2 * а2 * 2√3 * а
Парами сокращаем а и 2
r =
а2 * а2 * 2√3 * а
И в итоге получаем :
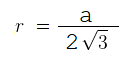
Радиус описанной окружности равностороннего треугольника
С описанной окружностью доказывается аналогично, лишь с той разницей, что радиус больше в два раза:
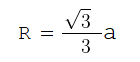
Или :
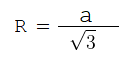
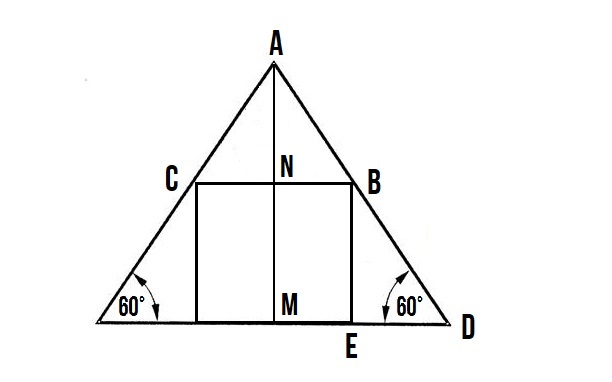
Задача : Вписанный квадрат в равносторонний треугольник.
Докажите, что вписанный квадрат в равносторонний треугольник делит одним углом, сторону треугольника пополам или не делит.
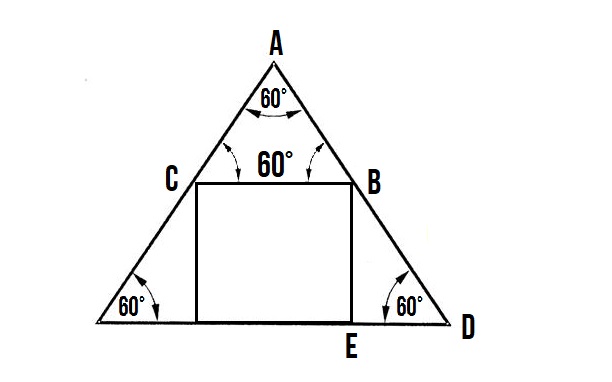
Решение задачи :
Мы знаем, что в равностороннем треугольнике все углы равны 60 :
180°/3 = 60°
И если мы посмотрим на треугольник
ABC
, то поскольку, все углы данного разностороннего треугольника равны 60°,
То стороны у этого треугольника будут равны между собой.
И одна из сторон совпадает со стороной квадрата.
Поэтому сторона «
AB
» равна стороне квадрата «
BC
» и стороне «
BE
«
Но «
BE
» не равна «
BD
«. Катет всегда будет меньше гипотенузы.
Если «
BE
» не равно «
BD
«, то «
BD
» не равно «
AB
«, что означает, что точка B не находится в середине отрезка «
AD
«.
Отсюда мы делаем вывод :
Угол вписанного квадрата не делит сторону равностороннего треугольника пополам!
Периметр равностороннего треугольника формула
Напишите «формулу периметра равностороннего треугольника»:
Обозначается периметр буквой P
Сторону обозначим через — а
Поскольку все стороны у равностороннего треугольника равны,
то периметр равностороннего треугольника будет равен :
3 умноженное на сторону а треугольника:
Формула периметра равностороннего треугольника
P = 3a
Конечно, можно еще представить данную формулу таким образом:
P = a + a + a
Но такого написания, я никогда не встречал.
Задача: найти высоту равностороннего если известна сторона вписанного квадрата.
Условие задачи :
Известна сторона «CB» вписанного квадрата, требуется найти высоту равностороннего треугольника «AM».
В пункте №6 и подпункте 4, мы вывели, что :
Сторона «AB» равна стороне квадрата «BC» и стороне «BE»
Поэтому, высота «AN» маленького треугольника будет равна :
И далее мы уже можем вывести высоту треугольника :
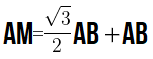
Задача: найти сторону равностороннего треугольника через площадь.
Условие задачи :
Известна площадь равностороннего треугольника «S», требуется узнать его сторону «а».
Я уже вывел площадь равностороннего треугольника в этом пункте, там же было доказательство!
Нам понадобится данная формула для решения выше озвученной задачи!
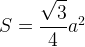
Нам всего-то навсего нужно выразить сторону «а» через «S»
S = √3 4*a²
Умножаем обе стороны на
4√3
Справа, в выражении дробь сократится, а слева появится данная дробь в перевернутом виде:
S* 4√3 = a²
Далее, чтобы получить сторону через площадь, нам нужно извлечь корень :
Преобразуем :
Преобразуем еще раз:
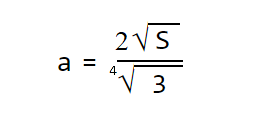
Ответ задачи : найти сторону равностороннего треугольника через площадь.
Сторона равностороннего треугольника равна корню из площади умноженное на 2, и деленное на корень 4 степени из 3.
Задача: если радиус описанной окружности в 2 раза больше радиуса вписанной окружности то треугольник равносторонний
Повстречал вот такой поисковый запрос :
«если радиус описанной окружности в 2 раза больше радиуса вписанной окружности то треугольник равносторонний«
Данную формулировку можно перефразировать и будет выглядеть совсем по другому:
Докажите, что радиус вписанной окружности равностороннего треугольника больше в два раза, радиуса описанной окружности
Вообще… эта одна из самых простых задач!
А почему, вы узнаете дальше.
Для доказательства данного утверждения нам понадобится :
Радиус вписанной окружности равностороннего треугольника, о котором я рассказывал здесь :
И второе — это радиус вписанной окружности равностороннего треугольника, о котором я рассказывал здесь : :
Далее — нужно разделить больший радиус на меньший:
Как вы наверное знаете, что при делении одной дроби н вторую существует правило, по которому вторую дробь нужно перевернуть и знак будет умножить…
После этого, смотрим, что можно сократить
Сокращаются квадратный корень из 3.
Сторона «а».
6 и 3, сокращаются только на 3. Сверху остается 2.
И вообще… из всех только и остается 2.
Т.е. вот мы и доказали, что :
Радиус вписанной окружности равностороннего треугольника больше в два раза, радиуса описанной окружности
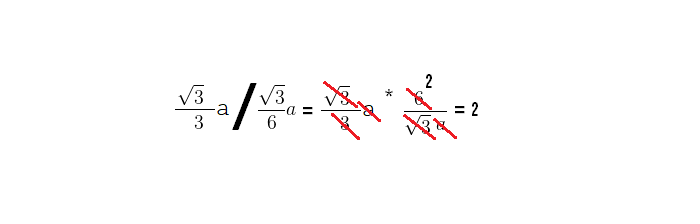


















![{displaystyle p^{4}+q^{4}+t^{4}=3left[left(R^{2}+L^{2}right)^{2}+2R^{2}L^{2}right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b9926a561be54775a0fa6d3c7fc03ccf00c2378)













 высоты, медианы и биссектрисы равностороннего треугольника равны:
высоты, медианы и биссектрисы равностороннего треугольника равны: