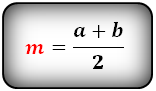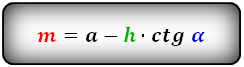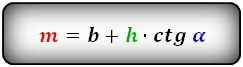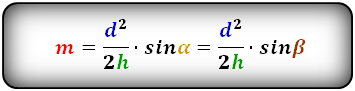Как найти углы при средней линии трапеции

Трапеция —  геометрическая фигура представляет собой выпуклый четырехугольник с параллельными
противоположными сторонами. Они называются основаниями. Две другие стороны — боковые.
Трапеция, у которой они одинакового размера, называется равнобедренной. Если одна из боковых сторон
образует у основания угол в 90 градусов-прямоугольной.

Прямая линия, проведенная от одного основания
к другому, именуется высотой трапеции. Величина ее высчитывается делением суммы оснований на 2.
Диагонали — это отрезки, соединяющие противоположные углы фигуры. У равнобедренной трапеции
они равны по длине. Средняя линия-прямая, делящая пополам боковые стороны.

  • Угол трапеции при основании через высоту и прилегающую
    боковую сторону
  • Угол трапеции через нижнее основание, боковую сторону и
    диагональ
  • Угол равнобедренной трапеции через нижнее основание,
    среднию линию и боковую сторону
  • Угол равнобедренной трапеции через среднию линию, верхнее
    основание и боковую сторону
  • Острый угол при нижнем основании прямоугольной трапеции
    через высоту и два основания
  • Острый угол при нижнем основании прямоугольной трапеции
    через два основания и боковую сторону

Угол трапеции при основании через высоту и прилегающую боковую сторону

Рис 1

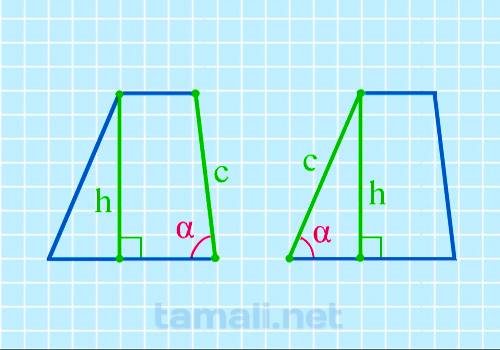
Введем обозначения: h-высота, с — боковая сторона. Угол трапеции α при основании вычисляется с
помощью формулы

sin α = h/с

где: h — высота трапеции, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Заменим буквенные обозначения условными цифрами. Пример: если высота равна
9см, боковая сторона-11см, получим: sin α = 9 / 11 = 0,818 , отсюда α =
55º. Указанное значение находим в таблице синусов. Данный показатель синуса угла соответствует
величине 55 градусов.

Через нижнее основание, среднию линию и боковую сторону в равнобедренной трапеции

Рис 3

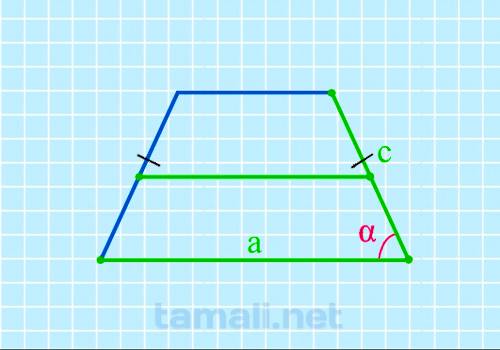
Угол равнобедренной трапеции через нижнее основание, среднюю линию и боковую сторону находится по
формуле:

cos α = (2a-2m) / 2c

где а — нижнее основание, m — средняя линия, с — боковая сторона.

Цифр после
запятой:

Результат в:

Пример.Заменим буквы условными цифровыми значениями. Если нижнее основание равно 8
см, средняя линия-6, а боковая сторона-4,8 см, то косинус угла равен 0,41666, что соответствует 65
градусам. cos α = (2 * 8 — 2 * 6) / 2 * 4,8 = 0, 41666, отсюда α =
65º. Равнобедренная трапеция — геометрическая фигура с нижними острыми углами. Это ее
особенность.

Угол трапеции, зная размер нижнего основания, боковой стороны и диагонали

Рис 2

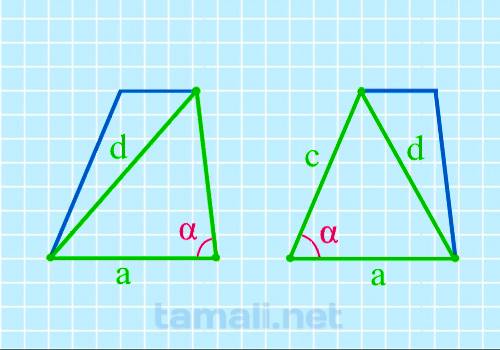
Если известны эти величины, воспользуемся формулой:

cos α= (a²+c²-d²) / 2ac

где а-нижнее основание, d-диагональ, с-боковая сторона.

Цифр после
запятой:

Результат в:

Пример. При условной величине нижнего основания 4 см, диагонали — 5.7 см,
боковой стороны — 4,4 см косинус равняется 0,081534, что соответствует углу 85 градусов по
таблице функций. cos α= (4² + 4,4² — 5,7²) / 2*4*4,4 = 0,081534,
отсюда α = 85º.

Через среднюю линию, верхнее основание и боковую сторону в равнобедренной трапеции

Рис 4

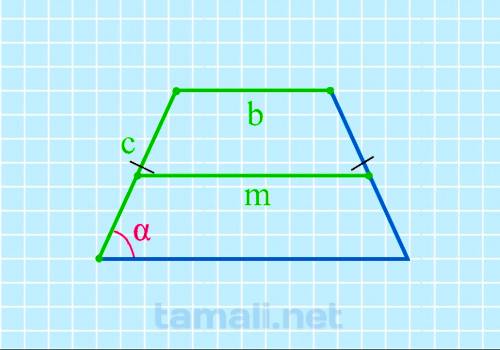
Нахождение угла равнобедренной трапеции через среднюю линию, верхнее основание и боковую сторону
выполняется по предложенной формуле:

cos α = (2m-2b) / 2c

где m — средняя линия, b — верхнее основание, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Введем условные цифровые значения. Допустим, что у равнобедренной трапеции
верхнее основание равно 4 см, средняя линия-6, боковая сторона-4 см. Косинус составляет 0,5.
Значение соответствует 60 градусам по таблице Брадиса. cos α = (2 * 6 — 2 * 4) / 2 * 4 = 0,5,
отсюда α = 60º

Вычисление острого угла при нижнем основании, если известны величины обоих оснований и боковой
стороны в прямоугольной трапеции

Рис 6

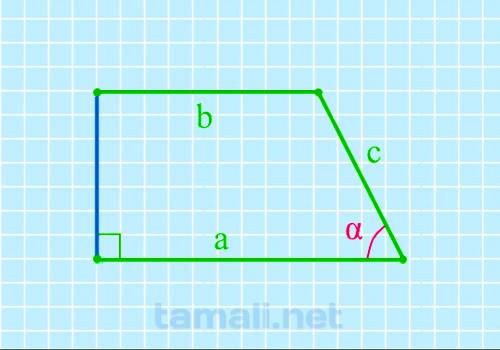
Находится по формуле

cos α = (a — b) / c

где a,b — основания, c — боковая сторона.

Цифр после
запятой:

Результат в:

Пример. Если буквенные выражения заменить условными цифровыми, получится наглядный
пример вычисления. Допустим, длина нижнего основания а 8 см, верхнего b-5,8 см, размер боковой
стороны с-4,8. Подставив в формулу цифровые значения, получим итог: косинус равен 0,45833.
Сравниваем показатель с таблицей вычисления Брадиса: он соответствует углу 63 градуса. cos α=(8 — 5,8) / 4,8 = 0,45833, отсюда α = 63º

Острый угол при нижнем основании, зная высоту и размеры двух оснований прямоугольной трапеции

Рис 5

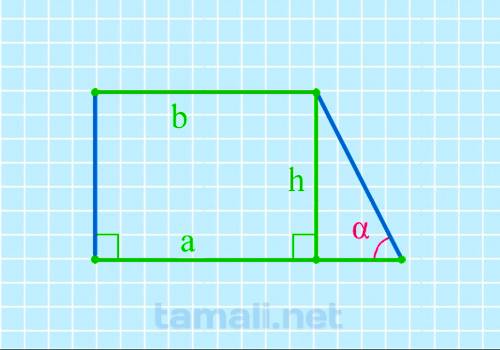
При известных указанных величинах воспользуемся следующей формулой:

tg(α) = h / (a-b)

где h — высота, a,b — верхнее и нижнее основания.

Цифр после
запятой:

Результат в:

Пример. Введя условные цифровые значения h = 15, a = 11, b = 10 получим tg(α) = 15 / (11-10) = 15. При вычислении получим значение тангенса: 15.
По таблице функций показатель соответствует 86 градусам.

Следует знать несколько закономерностей данной геометрической конструкции. У трапеции четыре угла,
общая сумма которых составляет 360 градусов.

Равнобедренная отличается двумя равными острыми, прилегающими к нижнему основанию, и тупыми
одинаковой величины-к верхнему. У прямоугольной трапеции два угла по 90 градусов, другие —
острый и тупой. Если он прилегает к нижнему основанию, величина такого угла определяется делением
высоты на разность между нижним и верхним основаниями. Угол трапеции при основании равен отношению
высоты к боковой стороне.

Источник

Определение трапеции

При изучении треугольников мы рассматривали свойства произвольных треугольников, но особое внимание уделяли частным случаям – прямоугольному, равнобедренному, равностороннему треугольникам.

Это связано с тем, что, во-первых, треугольники таким образом можно классифицировать (по сторонам, по углам), а, во-вторых, наличие дополнительной информации (равенство сторон, прямой угол и т. д.) позволяет получить более конкретные свойства для данного вида треугольников.

Такая же ситуация и с четырехугольниками. Мы мало можем сказать о четырехугольниках вообще (сумма углов, признаки вписанного и описанного четырехугольников). Но для некоторых видов четырехугольника смогли вывести довольно много важных и полезных свойств.

Мы классифицировали четырехугольники по наличию параллельности противоположных сторон. Параллельность даже одной пары сторон уже приводит к тому, что такой четырехугольник обладает большим количеством свойств. Такой четырехугольник называется трапецией (см. рис. 1), и его свойствам мы посвятим сегодняшний урок.

Рис. 1. Трапеция :

Трапеция и параллелограмм в классификации четырехугольников

Если оставить определение трапеции в таком виде: четырехугольник, у которого две стороны параллельны, – то мы получим, что на прошлом уроке мы изучали параллелограммы – частные случаи трапеции (см. рис. 2).

Рис. 2. Классификация, где параллелограмм – частный случай трапеции

Конечно, параллельность сразу двух пар сторон дает гораздо больше свойств – это очень сильное условие.

Поэтому параллелограмм и трапеция (в привычном нам понимании) сильно отличаются, и, чтобы не было путаницы, принято разделять эти два вида четырехугольников. Говорят, что трапеция – это четырехугольник, у которого две стороны параллельны, а две другие нет. При таком определении параллелограмм перестает быть частным случаем трапеции, а выделяется в отдельное семейство четырехугольников.

Такая классификация общепринята (см. рис. 3), ее мы и будем придерживаться, хотя первый вариант (параллелограмм – частный случай трапеции) тоже имеет право на жизнь.

Рис. 3. Классификация, где параллелограмм и трапеция – отдельные семейства четырехугольников

Мы уже неоднократно это подчеркивали: это все наши определения, поэтому мы можем сами выбирать, к какому классу относить ту или иную фигуру (как и то, является ли банан травой или деревом – природе все равно, классификация придумана человеком).

Свойства равнобедренной и прямоугольной трапеций

Расположим трапецию так, чтобы параллельные стороны были горизонтальны и большая из них находилась внизу. Чаще всего ее именно так и изображают (см. рис. 4).

Рис. 4. Трапецию чаще всего изображают так

Параллельные стороны называют основаниями – верхним и нижним (иногда используют слова «большее» и «меньшее», чтобы точно было понятно, о каком из них идет речь). Другие две стороны – боковыми.

Обратите внимание, что у трапеции всегда одно основание больше другого. Действительно, если бы основания трапеции были равны, то мы бы получили четырехугольник, у которого есть пара равных и параллельных сторон. Но тогда, по признаку параллелограмма, это уже была бы не трапеция, а параллелограмм (мы договорились, что множества этих четырехугольников не должны пересекаться).

Трапецию можно рассматривать как усеченный треугольник. Поэтому вполне логично, что для нее есть похожая схема классификации – по равенству боковых сторон и по наличию прямого угла (даже названия трапеций будут совпадать с названиями аналогичных видов треугольников).

Если боковые стороны трапеции равны, то она называется равнобедренной (или равнобокой) (см. рис. 5). Если один угол трапеции прямой, то она называется прямоугольной (см. рис. 6).

Рис. 5. Равнобедренная трапеция

Рис. 6. Прямоугольная трапеция

По картинкам можно предположить, что:

  1. в равнобедренной трапеции углы при одном основании равны;
  2. в прямоугольной трапеции будет не один, а сразу два прямых угла.

Докажем, что в равнобедренной трапеции   углы  (см. рис. 7).

Рис. 7. Равнобедренная трапеция  

Доказательство

Через точку  проведем прямую, параллельную . Она пересечет нижнее основание в точке .

Рис. 8. Прямая  параллельная

Тогда  – параллелограмм (), следовательно, . Но, по условию, , значит, . Тогда треугольник  равнобедренный. Значит, углы . Но углы , как соответственные при параллельных прямых. Значит, углы .

Доказано.

Несложно доказать, что равны будут не только углы , но и углы  (они дополняют углы  и  до  как внутренние односторонние).

Верно и обратное утверждение: если у трапеции равны углы при основании, то она равнобедренная. Докажите его самостоятельно, проведя точно такое же дополнительное построение.

Докажем свойство равнобедренной трапеции другим способом, чтобы подчеркнуть аналогию трапеции и треугольника.

Доказательство (другой способ)

Продлим боковые стороны  и  до пересечения (поскольку боковые стороны трапеции непараллельны по определению, то они обязательно пересекутся) в точке  (см. рис. 9).

Рис. 9. Продленные боковые стороны  и  пересекаются в точке

Прямые  и  – параллельные прямые, а значит, по обобщенной теореме Фалеса, они отсекают на сторонах угла  пропорциональные отрезки:

Но отрезки  (т. к. трапеция равнобедренная), значит, раз равны знаменатели, то равны и числители равных дробей:

Но тогда треугольник  равнобедренный:

А значит, у него равны углы при основании:

Доказано.

Эти два дополнительных построения: отрезок, параллельный боковой стороне, и продление боковых сторон до их точки пересечения – два стандартных инструмента, которые могут использоваться для решения различных задач, причем не только с равнобедренной, но и с произвольной трапецией.

Еще один полезный инструмент – отрезок, параллельный одной из диагоналей трапеции. В этом случае получается треугольник, длины сторон которого совпадают с длинами диагоналей, а третья сторона равна сумме длин оснований (т. к.  – параллелограмм: , , а значит, ) (см. рис. 10). При решении некоторых задач это может оказаться полезным, но подробно обо всех этих инструментах мы поговорим во время решения задач.

Рис. 10. Отрезок  параллелен

Посмотрим теперь на диагонали равнобедренной трапеции. В силу симметрии чертежа понятно, что диагонали равны (см. рис. 11). Но докажем это утверждение строго.

Рис. 11. У равнобедренной трапеции диагонали равны

Доказательство

Рассмотрим два треугольника:  и  (см. рис. 12).

Рис. 12. Рассматриваемые треугольники  и

У них есть три равных элемента:

  1.  (как стороны равнобедренной трапеции);
  2.  – общая сторона;
  3. углы  (как углы при основании в равнобедренной трапеции – только что доказали это свойство).

Значит, треугольники равны по первому признаку. Но тогда .

Доказано.

Вернемся к утверждению о свойстве прямоугольной трапеции: в прямоугольной трапеции два прямых угла.

Углы при боковой стороне являются внутренними односторонними при параллельных прямых (основаниях трапеции). Значит, их сумма равна  (см. рис. 13).

Рис. 13. В трапеции :

Понятно, что если один угол прямой, то и второй при этой боковой стороне тоже прямой:

Но выполняется и более общее свойство. В любой трапеции сумма углов при каждой из боковых сторон равна :

Средняя линия трапеции

В треугольниках мы рассматривали такой элемент, как средняя линия – отрезок, соединяющий середины любых двух его сторон (см. рис. 14).

Рис. 14. Отрезок  – средняя линия треугольника

По аналогии такой же элемент можно ввести и для трапеции. При этом он окажется полезным инструментом для описания различных свойств трапеции.

Нас будет интересовать отрезок, соединяющий середины именно боковых сторон трапеции. Такой отрезок называется средней линией трапеции (см. рис. 15).

Рис. 15. Отрезок  – средняя линия трапеции

Поскольку свойства средних линий треугольника и трапеции очень похожи, то рассмотрим их вместе.

Линия, соединяющая середины противоположных оснований трапеции

Мы будем изучать свойства средней линии трапеции – линии, которая соединяет середины боковых сторон. Но ведь можно соединить середины двух других сторон трапеции – оснований (см. рис. 16).

Рис 16. Линия, соединяющая середины противоположных оснований трапеции

Что можно сказать про эту линию? Оказывается, у нее тоже есть любопытное свойство. Оказывается, что на этой линии лежат не только середины оснований трапеции, но и точка пересечения боковых сторон и даже точка пересечения диагоналей трапеции, причем это свойство выполняется для любых трапеций.

Чаще всего доказательство того факта, что несколько точек лежат на одной прямой выполняется с помощью удобного инструмента – векторов, который мы будем изучать в  классе. Но и сейчас, в принципе, доказательство этого утверждения нам под силу.

Доказательство

Рассмотрим трапецию , боковые стороны которой пересекаются в точке . Пусть  – середина основания . Продлим прямую  до пересечения с  в точке  (см. рис. 17).

Рис. 17. Трапеция : , ,

Треугольники  и , а также  и  подобны (в каждой паре есть общие углы, а оставшиеся два равны как соответственные при параллельных прямых и секущей). Причем у них одинаковый коэффициент подобия:

Действительно, из первой пары:

Из второй пары:

Приравнивая правые части, получаем:

Но  ( – середина ), значит, равны и знаменатели равных дробей:

Т. е.  – середина . Значит, середины оснований  и  и точка пересечения боковых сторон  лежат на одной прямой.

Доказано.

Точно так же можно доказать и то, что точка  пересечения диагоналей лежит на этой прямой (см. рис. 18).

Рис. 18. Точка пересечения диагоналей лежит на линии, соединяющей середины противоположных оснований трапеции

Доказательство

Рассмотрим прямую  (где  – середина ) и ее точку пересечения с  – точку .

По аналогии: треугольники  и , а также  и  попарно подобны (вертикальные углы + две пары внутренних накрест лежащих).

Из первой пары:

Из второй пары:

Приравнивая правые части, получаем:

Но , значит, . Снова получаем, что точка  должна быть серединой . Значит, середины оснований ,  и точка пересечения диагоналей  лежат на одной прямой.

Доказано.

Но через любые две точки проходит только одна прямая, значит, через точки  и  проходит прямая, на которой лежат и точка , и точка . Мы доказали, что все  точки лежат на одной прямой (см. рис. 19).

Рис. 19. На линии, соединяющей середины противоположных оснований трапеции, лежат середины оснований трапеции (точки  и ), точка пересечения боковых сторон (точка ) и точка пересечения диагоналей трапеции (точка )

Помимо того, что этот факт можно использовать при решении различных задач, стоит заметить, что даже три произвольные точки редко оказываются одновременно на одной прямой (вспомните: если бросить три случайные точки на стол, то они наверняка образуют треугольник, т. е. не будут лежать на одной прямой). А уж четыре точки – это еще бо́льшая редкость. Так что с точки зрения математики этот факт примечателен сам по себе.

Теорема о средней линии треугольника

Проведем среднюю линию треугольника (см. рис. 20). Похоже, что она параллельна основанию. Посмотрим, так ли это.

Рис. 20. Отрезок  – средняя линия треугольника

Можно доказать это утверждение, используя подобие треугольников:

Значит:

Но раз равны соответственные углы при секущих, то прямые  и  параллельны.

Более того, поскольку мы знаем коэффициент подобия треугольников, то получили еще одно свойство средней линии треугольника:

Т. е. средняя линия треугольника параллельна основанию и равна его половине.

Это утверждение можно было доказать и по-другому, например продлив отрезок  за точку  так, чтобы  (см. рис. 21). А затем доказать, что  – параллелограмм. Можете попробовать сделать это самостоятельно.

Рис. 21. Отрезок  продлен за точку  так, что

Для нас же важен результат, теорема о средней линии треугольника звучит так: средняя линия треугольника параллельна основанию и равна его половине.

Верно и обратное утверждение, которое формулируется так: отрезок, проведенный через середину боковой стороны треугольника параллельно основанию, является средней линией треугольника (т. е. проходит через середину другой боковой стороны).

Если предположить, что этот отрезок не совпадает со средней линией, то через эту точку  проходят сразу две прямые, параллельные основанию (отрезок и средняя линия), а это, как мы знаем, противоречит пятому постулату Евклида, поэтому предположение неверное. Значит, отрезок является средней линией треугольника.

Теорема о средней линии трапеции

Теперь вернемся к трапеции. Проведем среднюю линию (см. рис. 22). Очень похоже, что она тоже параллельна основанию, вернее, обоим основаниям.

Рис. 22. Отрезок  – средняя линия трапеции

Доказательство

Докажем это утверждение. Для этого проведем прямую  до пересечения с основанием  в точке . Рассмотрим полученные треугольники  и  (см. рис. 23).

Рис. 23. Рассматриваемые треугольники  и

По определению средней линии , углы  (как вертикальные), углы  (как внутренние накрест лежащие при параллельных основаниях трапеции). Значит, треугольники равны по второму признаку равенства (сторона и два угла). Значит, . Но тогда  – средняя линия треугольника , значит:

Кроме того:

 – из доказанного равенства треугольников  и .

Доказано.

Получаем теорему о средней линии трапеции: средняя линия трапеции параллельна основаниям и равна их среднему арифметическому (полусумме).

Верно и обратное утверждение, которое формулируется так: отрезок, проведенный через середину боковой стороны трапеции параллельно ее основаниям, является средней линией (т. е. проходит через середину другой боковой стороны).

Доказательство это обратного утверждения точно такое же, как и аналогичного утверждения для треугольника.

Другое доказательство теоремы о средней линии трапеции

Попробуем доказать свойства средней линии трапеции по аналогии со свойствами средней линии треугольника. Для этого снова используем уже известный нам инструмент – продлим боковые стороны трапеции до пересечения в точке  (см. рис. 24).

Рис. 24. Боковые стороны трапеции продлены до пересечения в точке

По обобщенной теореме Фалеса параллельные прямые  и  отсекают на сторонах угла  пропорциональные отрезки:

Или:

Но обе части этого равенства можно умножить на :

Но тогда отрезки  и  тоже параллельны (обратная теорема Фалеса: они отсекают на сторонах угла пропорциональные отрезки, а значит, параллельны).

Можно доказать это и через подобие треугольников  и :

где угол  общий – подобие по первому признаку. Значит:

Правда, мы не доказали, что средняя линия трапеции равна полусумме оснований, но это тоже можно сделать, хотя и довольно громоздко.

Из подобия треугольников  и  получим:

Из подобия треугольников  и  получим:

Из первого равенства:

Подставляем во второе:

Умножим обе части равенства на :

Или:

Сформулируем еще раз обе теоремы о средних линиях:

  1. средняя линия треугольника параллельна основанию и равна его половине;
  2. средняя линия трапеции параллельна основаниям и равна половине их суммы.

Это очень похожие утверждения. Более того, если треугольник считать предельным случаем трапеции, у которой верхнее основание стянулось в точку, то формула для треугольника получается из формулы для трапеции, если считать длину верхнего основания равной нулю.

Площадь трапеции

Еще одной важной характеристикой любой фигуры на плоскости является площадь. Трапеция не исключение. Конечно, мы можем использовать общую формулу площади для всех четырехугольников:

Но хочется получить специфическую формулу, в которой учтены свойства трапеции, выделяющие ее из множества произвольных четырехугольников.

Раз уж мы проводим аналогию между трапецией и треугольником, то нам, видимо, не обойтись без высоты при выводе формулы площади трапеции.

Действительно, раз основания трапеции параллельны, то расстояние между ними постоянно (см. рис. 25) – из какой бы точки одного основания мы ни опустили перпендикуляр на другое, он, во-первых, будет перпендикулярен первому основанию (сумма односторонних углов равна ), а, во-вторых, его длина будет одинакова и не будет зависеть от выбранной точки.

Рис. 25. Расстояние между основаниями трапеции постоянно

Любой такой отрезок, перпендикулярный основаниям трапеции, называется высотой трапеции (см. рис. 26). Чаще всего высоту трапеции проводят из одной из вершин меньшего основания.

Рис. 26. Высота трапеции

Если провести две такие высоты из вершин меньшего основания, то трапеция разобьется на прямоугольник со сторонами  и , а также на два прямоугольных треугольника. У каждого из них один из катетов будет . Обозначим второй катет первого треугольника как , тогда длина второго катета второго треугольника будет равна  (см. рис. 27).

Рис. 27. Введенные обозначения

Запишем площадь трапеции как сумму площадей прямоугольника и двух прямоугольных треугольников:

Площадь трапеции равна произведению полусуммы ее оснований на высоту:

Эту формулу можно получить и по-другому – если продлить боковые стороны трапеции до пересечения и вычислить площадь трапеции как разность площадей двух треугольников (см. рис. 28). Попробуйте сделать это самостоятельно.

Рис. 28. Площадь трапеции  можно вычислить как разность площадей треугольников  и

Поскольку мы знаем, что длина средней линии трапеции равна полусумме оснований, то эту формулу можно переписать так:

где  – средняя линия трапеции:

Т. е. площадь трапеции равна произведению средней линии на высоту.

Нетрудно и тут увидеть, что формула площади треугольника получается как предельный случай, если одно основание равно нулю:

Аналогично и формула площади параллелограмма получается как другой предельный случай, если основания равны друг другу:

Свойства вписанной и описанной трапеций

Теперь, когда мы вывели основные свойства трапеции, ввели такие элементы, как средняя линия и высота, а также обсудили классификацию (равнобедренная и прямоугольные трапеции), можно поговорить еще о нескольких свойствах, которые могут оказаться полезными при решении задач.

Когда мы изучали параллелограммы и их частные случаи (прямоугольники, ромбы, квадраты), то говорили о симметрии некоторых из них. Есть ли у трапеций оси или центр симметрии?

Попробуйте сами убедиться, что ни у какой трапеции не может быть центра симметрии, а ось симметрии есть только у одного вида – у равнобедренных трапеций (см. рис. 29). И проходит эта ось через середины оснований, перпендикулярно им. Здесь тоже наблюдается аналогия с треугольниками: осью симметрии обладают только равнобедренные треугольники.

Рис. 29. Осевая симметрия есть только у равнобедренной трапеции

Еще один вопрос, который мы обсуждали, – вписанные и описанные параллелограммы. Попробуем дать на него ответ и для трапеций.

Начнем с вписанной трапеции (см. рис. 30).

Рис. 30. Вписанная трапеция

Свойство вписанного четырехугольника: суммы противоположных углов равны . Но у любой трапеции суммы смежных углов при боковых сторонах равны . Значит, если трапеция вписана, то:

Значит:

Аналогично:

Значит, вписанная трапеция обязательно будет равнобедренной.

Об описанной трапеции какой-то дополнительной информации получить нельзя, поэтому остается пользоваться свойством описанного четырехугольника: суммы длин противоположных сторон равны.

Свойство равнобедренной трапеций, связанное с высотой

Проведем в равнобедренной трапеции  высоту . Проведем  параллельно  (рис. 31).

Рис. 31.  – высота равнобедренной трапеции ,

Т. к.  – параллелограмм (противоположные стороны попарно параллельны), то:

Но тогда  – равнобедренный треугольник, поэтому  – высота и медиана, получаем:

При этом:

Получаем:

Откуда:

Несложно получить, что длина  равна длине средней линии:

Первое равенство  понятно, если провести вторую высоту . Ясно, что отрезки  и  равны. При этом отрезок  равен основанию  ( – прямоугольник), значит:

Запоминать эти формулы необязательно, при необходимости вы всегда сможете легко их вывести.

Заключение

На этом уроке мы подробно разобрали еще один вид четырехугольников – трапеции. Обсудили их свойства, классификацию. Следующий урок мы посвятим практике и решению задач, в которых встречаются различные четырехугольники.

Списоклитературы

  1. Александров А.Д., Вернер А.Л., Рыжик В.И. Геометрия, 8 класс. Учебник. –М.: «Просвещение», 2018.
  2. Бутузов В.Ф., Кадомцев С.Б., Прасолов В.В./Под ред. Садовничего В.А. Геометрия, 8 класс. Учебник. – М.:«Просвещение», 2018.
  3. Мерзляк А.Г., Полонский В.Б., Якир М.С., Геометрия, 8 класс. Учебник. –М.: издательский центр «ВЕНТАНА-ГРАФ», 2018.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

  1. Интернет-портал yaklass.ru (Источник)
  2. Интернет-портал math-prosto.ru (Источник)
  3. Интернет-портал «схемо.рф» (Источник)

Домашнеезадание

  1. В прямоугольной трапеции острый угол равен , а меньшее основание и бо́льшая боковая сторона равны по . Найти длину большего основания.
  2. Острый угол равнобедренной трапеции равен , боковая сторона равна , а большее основание равно . Найти длину средней линии трапеции.
  3. Длины оснований трапеции относятся как , а ее высота равна . Вычислить длины оснований трапеции, если ее площадь равна .
Источник

Виды трапеции

  1. Произвольная трапеция – это четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна)
  2. Равнобедренная трапеция – это такая трапеция, у которой боковые стороны равны
  3. Прямоугольная трапеция – это такая трапеция, у которой есть прямые углы при боковой стороне

Свойства трапеции

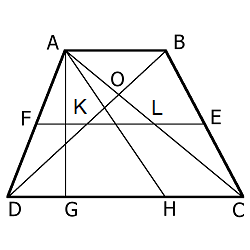
  1. Средняя линия трапеции (FE) параллельна основаниям и равна их полусумме
    $$
    FE = {AB + DC over 2}
    $$
  2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне
    Например: биссектриса AH отсекает на основании DC отрезок DH , который равен боковой стороне AD
  3. Треугольники AOB и DOC, образованные отрезками диагоналей и основаниями трапеции, подобны
  4. Треугольники AOD и BOC, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь
  5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон (AD + BC = AB + DC)
  6. Отрезок (KL), соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии, т.е.
    $$
    KL = {DC — AB over 2}
    $$
  7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой
  8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности

Свойства и признаки равнобедренной трапеции

  1. В равнобедренной трапеции углы при любом основании равны (∠ADC = ∠DCB и ∠DAB = ∠ABC)
  2. В равнобедренной трапеции длины диагоналей равны (AC = BD)
  3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная
  4. Около равнобедренной трапеции можно описать окружность
  5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований

Формулы площади произвольной трапеции

Площадь трапеции через основания и высоту

$$
S = {AB + DC over 2} * AG
$$

Площадь трапеции через среднюю линию и высоту

$$
S = FE * AG
$$

Площадь трапеции через диагонали и угол между ними

$$
S = {AC * BD over 2} * sin(∠AOD) = {AC * BD over 2} * sin(∠AOB)
$$

Площадь трапеции через четыре стороны

$$
S = {DC + AB over 2} * sqrt{AD^2 — ({(DC — AB)^2 + AD^2 — BC^2 over 2 * (DC — AB)})^2}
$$

Формулы площади равнобедренной трапеции

Площадь трапеции через стороны

$$
S = {DC + AB over 2} * sqrt{AD^2 — {(DC — AB)^2 over 4}}
$$

Площадь трапеции через стороны и угол

$$
S = AD * sin(∠ADC) * (DC — AD * cos(∠ADC))
$$
$$
S = AD * sin(∠ADC) * (AB + AD * cos(∠ADC))
$$

Площадь трапеции через диагонали и угол между ними

$$
S = {AC^2 over 2} * sin(∠AOD) = {AC^2 over 2} * sin(∠BOC)
$$

Площадь трапеции через среднюю линию, боковую сторону и угол при основании

$$
S = FE * AD * sin(∠ADC) = FE * AD * sin(∠DAB)
$$

Площадь трапеции если в нее вписана окружность

$$
S = {4 * R_В^2 over sin(∠ADC)} = {4 * R_В^2 over sin(∠DAB)}
$$
$$
S = {AB * DC over sin(∠ADC)} = {AB * DC over sin(∠DAB)}
$$

Формулы сторон произвольной трапеции

Основание через другое основание и среднюю линию

$$
AB = 2 * FE — DC
$$
$$
DC = 2 * FE — AB
$$

Основание через другое основание, диагонали и угол между ними

$$
DC = {AC * BD over AG} * sin(∠AOD) — AB
$$
$$
AB = {AC * BD over AG} * sin(∠AOD) — DC
$$

Длины сторон

$$
DC = AB + AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
AB = DC — AG * (ctg(∠ADC) + ctg(∠BCD))
$$
$$
DC = AB + AD * cos(∠ADC) + BC * cos(∠BCD)
$$
$$
AB = DC — AD * cos(∠ADC) — BC * cos(∠BCD)
$$
$$
AD = {AG over sin(∠ADC)}
$$
$$
BC = {AG over sin(∠BCD)}
$$

Формулы сторон равнобедренной трапеции

Длины сторон

$$
AD = {AG over sin(∠ADC)}
$$
$$
AD = {DC — AB over 2 * cos(∠ADC)}
$$
$$
DC = AB + 2 * AG * ctg(∠ADC)
$$
$$
AB = DC — 2 * AG * ctg(∠ADC)
$$
$$
DC = AB + 2 * AB * cos(∠ADC)
$$
$$
AB = DC — 2 * AB * cos(∠ADC)
$$

Длина основания через диагональ, боковую сторону и другое основание

$$
DC = {AC^2 — DA^2 over AB}
$$
$$
AB = {AC^2 — DA^2 over DC}
$$

Длина боковой стороны через диагональ и основания

$$
AD = sqrt{AC^2 — AB * DC}
$$

Длина основания через высоту, другое основание, диагонали и угол между ними

$$
DC = {AC^2 over AG} * sin(∠AOD) — AB
$$
$$
AB = {AC^2 over AG} * sin(∠AOD) — DC
$$

Длина основания через высоту, другое основание и площадь трапеции

$$
DC = {2 * S over AG} — AB
$$
$$
AB = {2 * S over AG} — DC
$$

Длина боковой стороны через площадь трапеции, среднюю линию и угол при основании

$$
AD = {S over FE * sin(∠ADC)} = {S over FE * sin(∠DAB)}
$$

Длина боковой стороны через площадь трапеции, основания и угол при основании

$$
AD = {2 * S over (AB + DC) * sin(∠ADC)}
$$
$$
AD = {2 * S over (AB + DC) * sin(∠DAB)}
$$

Формулы сторон прямоугольной трапеции

Длины оснований

$$
DC = AB + BC * cos(∠BCD) = AB + AD * ctg(∠BCD)
$$
$$
AB = DC — BC * cos(∠BCD) = DC — AD * ctg(∠BCD)
$$
$$
DC = AB + sqrt{BC^2 — AD^2}
$$
$$
AB = DC — sqrt{BC^2 — AD^2}
$$

Длина основания через боковую сторону, другое основание, диагонали и угол между ними

$$
DC = {AC * BD over AD} * sin(∠AOD) — AB
$$
$$
AB = {AC * BD over AD} * sin(∠AOD) — DC
$$

Длина основания через площадь трапеции, другое основание и высоту

Высота в прямоугольной трапеции равна стороне, которая перпендикулярна основаниям (AD = AG)
$$
DC = {2 * S over AD} — AB
$$
$$
AB = {2 * S over AD} — DC
$$

Формулы диагоналей произвольной трапеции

Длина диагоналей через четыре стороны

$$
BD = sqrt{BC^2 + DC * AB — {DC * (BC^2 — AD^2) over DC — AB}}
$$
$$
AC = sqrt{AD^2 + DC * AB — {DC * (AD^2 — BC^2) over DC — AB}}
$$

Длина диагоналей по теореме косинусов

$$
BD = sqrt{DC^2 + BC^2 — 2 * DC * BC * cos(∠BCD)}
$$
$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * AD * cos(∠ADC)}
$$

Длина диагоналей через высоту

$$
BD = sqrt{AG^2 + (DC — AG * ctg(∠BCD))^2}
$$
$$
BD = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$
$$
BD = sqrt{DC^2 + BC^2 — 2 * DC * sqrt{BC^2 — AG^2}}
$$
$$
AC = sqrt{AG^2 + (DC — AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠BCD))^2}
$$
$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * sqrt{AD^2 — AG^2}}
$$

Длина диагоналей через стороны и другую диагональ

$$
BD = sqrt{AD^2 + BC^2 + 2 * DC * AB — AC^2}
$$
$$
AC = sqrt{AD^2 + BC^2 + 2 * DC * AB — BD^2}
$$

Длина диагоналей через высоту, основания, другую диагональ и угол между диагоналей

$$
BD = {AG * (DC + AB) over AC * sin(∠AOD)}
$$
$$
AC = {AG * (DC + AB) over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$

Длина диагоналей через площадь трапеции, другую диагональ и угол между диагоналей

$$
BD = {2 * S over AC * sin(∠AOD)}
$$
$$
AC = {2 * S over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$

Длина диагоналей через среднюю линию, высоту, другую диагональ и угол между диагоналей

$$
BD = {2 * FE * AG over AC * sin(∠AOD)}
$$
$$
AC = {2 * FE * AG over BD * sin(∠AOD)}
$$
$$
sin(∠AOD) = sin(∠AOB)
$$

Формулы диагоналей равнобедренной трапеции

Длина диагоналей через стороны

$$
AC = sqrt{AD^2 + AB * DC}
$$

Длина диагоналей по теореме косинусов

$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * AD * cos(∠ADC)}
$$
$$
AC = sqrt{DC^2 + AD^2 + 2 * DC * AD * cos(∠DAB)}
$$

$$
AC = sqrt{AB^2 + AD^2 — 2 * AB * AD * cos(∠DAB)}
$$
$$
AC = sqrt{AB^2 + AD^2 + 2 * AB * AD * cos(∠ADC)}
$$

Длина диагоналей

$$
AC = sqrt{AG^2 + FE^2}
$$
$$
AC = sqrt{AG^2 + {(DC + AB)^2 over 4 }}
$$
$$
AC = sqrt{{AG * (AB + DC) over sin(∠AOD)}} = sqrt{{2 * S over sin(∠AOD)}} = sqrt{{2 * FE * AG over sin(∠AOD)}}
$$

Длина диагоналей через высоту основание и угол при основании

$$
AC = sqrt{AG^2 + (DC — AG * ctg(∠ADC))^2}
$$
$$
AC = sqrt{AG^2 + (AB + AG * ctg(∠ADC))^2}
$$

Длина диагоналей через сторону и высоту

$$
AC = sqrt{DC^2 + AD^2 — 2 * DC * sqrt{AD^2 — AG^2}}
$$

Формулы диагоналей прямоугольной трапеции

$$
BD = sqrt{AD^2 + AB^2}
$$
$$
AC = sqrt{AC^2 + DC^2}
$$

Формулы средней линии произвольной трапеции

Длина средней линии через основания

$$
FE = {DC + AB over2}
$$

Длина средней линии через основание, высоту и углы при нижнем основании

$$
FE = DC — AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠ADC) + ctg(∠BCD) over 2}
$$

Длина средней линии через диагонали, высоту и угол между диагоналями

$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$

Длина средней линии через площадь и высоту

$$
FE = {S over AG}
$$

Формулы средней линии равнобедренной трапеции

Длина средней линии через основания

$$
FE = {DC + AB over2}
$$

Длина средней линии через основание, высоту и углы при нижнем основании

$$
FE = DC — AG * ctg(∠ADC) = AB + AG * ctg(∠ADC)
$$

Длина средней линии через основания, боковую сторону и высоту

$$
FE = DC — sqrt{AD^2 — AG^2} = AB + sqrt{AD^2 — AG^2}
$$

Длина средней линии через диагонали, высоту и угол между диагоналями

$$
FE = {AC^2 over 2 * AG} * sin(∠AOD) = {AC^2 over 2 * AG} * sin(∠AOB)
$$

Длина средней линии через площадь и боковую сторону

$$
FE = {S over AD * sin(∠ADC)}
$$

Формулы средней линии прямоугольной трапеции

Длина средней линии через основания, высоту и угол при нижнем основании

$$
FE = DC — AG * {ctg(∠BCD) over 2}
$$
$$
FE = AB + AG * {ctg(∠BCD) over 2}
$$

Длина средней линии через основания, боковую сторону и угол при нижнем основании

$$
FE = DC — BC * {cos(∠BCD) over 2}
$$
$$
FE = AB + BC * {cos(∠BCD) over 2}
$$

Длина средней линии через основания и боковые стороны

$$
FE = DC — {sqrt{BC^2 — AD^2} over 2}
$$
$$
FE = AB + {sqrt{BC^2 — AD^2} over 2}
$$

Длина средней линии через диагонали, высоту и угол между диагоналями

$$
FE = {AC * BD over 2 * AG} * sin(∠AOD)
$$
$$
FE = {AC * BD over 2 * AG} * sin(∠AOB)
$$

Формулы высоты произвольной трапеции

Длина высоты через четыре стороны

$$
AG = sqrt{AD^2 — ({(DC — AB)^2 + AD^2 — BC^2 over 2 * (DC — AB)})^2}
$$

Длина высоты через боковую сторону и прилегающий угол к основанию

$$
AG = AD * sin(∠ADC) = BC * sin(∠BCD)
$$

Длина высоты через диагонали и углы между ними

$$
AG = {AC * BD over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC * BD over AB + DC} * sin(∠AOB)
$$

Длина высоты через среднюю линию, диагонали и углы между ними

$$
AG = {AC * BD over 2 * FE} * sin(∠AOD)
$$
$$
AG = {AC * BD over 2 * FE} * sin(∠AOB)
$$

Длина высоты через площадь и основания

$$
AG = {2 * S over AB + DC}
$$

Длина высоты через площадь и среднюю линию

$$
AG = {S over FE}
$$

Формулы высоты равнобедренной трапеции

Длина высоты через по сторонам

$$
AG = sqrt{AD^2 — {(DC — AB)^2 over 4}}
$$

Длина высоты через боковую сторону и прилегающий угол к основанию

$$
AG = AD * sin(∠ADC)
$$

Длина высоты через основания и прилегающий угол к основанию

$$
AG = {DC — AB over 2} * tg(∠ADC)
$$

Длина высоты через диагонали и углы между ними

$$
AG = {AC^2 over AB + DC} * sin(∠AOD)
$$
$$
AG = {AC^2 over AB + DC} * sin(∠AOB)
$$

Длина высоты через площадь и основания

$$
AG = {2 * S over AB + DC}
$$

Длина высоты через площадь и среднюю линию

$$
AG = {S over FE}
$$

Формулы боковых сторон прямоугольной трапеции

Сторона AD

Сторона AD в прямоугольной трапеции равна высоте, поэтому все формулы высоты произвольной трапеции актуальны для стороны AD прямоугольной трапеции.

Сторона BC по трём сторонам

$$
BC = sqrt{AD^2 + (DC — AB)^2}
$$

Сторона BC через основания и угол ∠BCD

$$
BC = {DC — AB over cos(∠BCD)}
$$

Сторона BC через Сторону AD

$$
BC = {AD over sin(∠BCD)}
$$

Сторона BC через площадь, среднюю линию и угол ∠BCD

$$
BC = {S over FE * sin(∠BCD)}
$$

Сторона BC через площадь, основания и угол ∠BCD

$$
BC = {2 * S over (AB + DC) * sin(∠BCD)}
$$

Источник

Трапеция и ее свойства

Т. А. Унегова

Определения:

Трапеция — это называется четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.

Параллельные стороны называются основаниями трапеции, а непараллельные — боковыми сторонами трапеции.

Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.

Если боковые стороны равны, трапеция называется равнобедренной.

Высотой трапеции называется перпендикуляр, проведенный из любой точки одного из оснований трапеции к прямой, содержащей другое основание.

Трапеция называется вписанной в окружность, если каждая ее вершина принадлежит окружности.

Трапеция называется описанной вокруг окружности, если каждая ее сторона касается окружности.

Трапеция называется равнобедренной (равнобокой, равнобочной), если ее боковые стороны равны.

Трапеция, один из углов которой прямой, называется прямоугольной.

Теоремы о средней линии и диагоналях трапеции

Теорема 1. Средняя линия трапеции параллельна основаниям и равна их полусумме: m=displaystyle frac{a+b}{2}.

Теорема 2. Диагонали трапеции делят среднюю линию трапеции на три отрезка. Средний из них равен полуразности оснований, а два крайних равны между собой: EF=GH, ; FG=displaystyle frac{a-b}{2}.

Теорема 3. Средняя линия треугольника, составленного из диагоналей и суммы оснований трапеции, равна средней линии трапеции: PQ=MN.

Теорема 4. Четыре точки: середины оснований трапеции, точка пересечения ее диагоналей и точка пересечения продолжений ее боковых сторон — лежат на одной прямой.

Эта теорема называется также «Замечательное свойство трапеции».

Теорема 5. Диагонали трапеции делят ее на четыре треугольника. Два из них, содержащие боковые стороны, равновелики (имеют равные площади), а два других, содержащие основания, подобны.

Теоремы о площади трапеции

Теорема 6. Площадь трапеции равна произведению полусуммы ее оснований на высоту: S=displaystyle frac{a+b}{2}cdot h.

Теорема 7. Площадь трапеции равна произведению ее средней линии на высоту: S=mh.

Теорема 8. Площадь трапеции (как и всякого выпуклого четырехугольника) равна половине произведения ее диагоналей на синус угла между ними: S=displaystyle frac{1}{2}d_1d_2{sin alpha }, где d_1=AC, d_2=BD, alpha =angle BOA. (Вместо angle BOA можно брать angle BOC.)

Теорема 9. Если в трапецию можно вписать окружность, то (как и для всякого описанного многоугольника) площадь трапеции равна произведению ее полупериметра на радиус вписанной окружности: S=pr. Таким образом, S=displaystyle frac{a+b+c+d}{2}cdot r.

Теорема 10. Площадь трапеции равна площади треугольника, составленного из диагоналей и суммы оснований этой трапеции. (Сравни эту теорему и теорему 3.)

Теоремы о вписанных и описанных трапециях

Теорема 11. Если трапеция вписана в окружность, то она равнобедренная. И наоборот, если трапеция равнобедренная, то около нее можно описать окружность.

Теорема 12. Если трапеция описана около окружности, то сумма оснований трапеции равна сумме ее боковых сторон.

Задачи ЕГЭ и ОГЭ по теме: Трапеция

Задача 1.

Найдите высоту трапеции ABCD, опущенную из вершины B, если стороны квадратных клеток равны sqrt{2}.

Решение:

Высота трапеции— это отрезок, перпендикулярный ее основаниям. Проведем высоту из вершины B. Так как сторона квадратной клетки равна sqrt{2} , то по теореме Пифагора получаем, что h=2.

Ответ: 2.

Задача 2.

Основания трапеции равны 18 и 6, боковая сторона, равная 7, образует с одним из оснований трапеции угол {150}^{{}^circ }. Найдите площадь трапеции.

Решение:

Углы angle ABC и angle BAH — односторонние, их сумма равна {180}^{{}^circ }, и тогда angle BAH =30{}^circ .

Из vartriangle ABH найдем высоту BH. Катет, лежащий против угла в {30}^{{}^circ }, равен половине гипотенузы. Получаем, что BH = 3,5.

Площадь трапеции равна S=displaystyle frac{6+18}{2}cdot 3,5=42.

Ответ: 42.

Задача 3.

Основания трапеции равны 4 и 10. Найдите больший из отрезков, на которые делит среднюю линию этой трапеции ее диагональ.

Решение:

Что можно увидеть на чертеже? Можно сказать, что изображена трапеция ABCD, и в ней проведена средняя линия. А можно увидеть и другое — два треугольника, ABC и ACD, в которых проведены средние линии.

Напомним, что средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. Средняя линия треугольника параллельна третьей его стороне и равна половине этой стороны. Из vartriangle ACD находим, что x=5.

Ответ: 5.

Задача 4.

Основания трапеции равны 3 и 2. Найдите отрезок, соединяющий середины диагоналей трапеции.

Решение:

Проведем PQ — среднюю линию трапеции, PQ = 2,5 и PQparallel BC. Отсюда получаем, что M- середина отрезка AC, то есть PM — средняя линия треугольника ABC и PM = 1. Аналогично, NQ = 1.

x=MN=PQ-PM-NQ=0,5.

Ответ: 0,5.

Задача 5.

Прямая, проведенная параллельно боковой стороне трапеции через конец меньшего основания, равного 4, отсекает треугольник, периметр которого равен 15. Найдите периметр трапеции.

Решение:

Периметр треугольника равен сумме его сторон, то есть a+b+c=15.

Периметр трапеции равен

a+b+4+c+4=left(a+b+cright)+8=15+8=23.

Ответ: 23.

Задача 6.

В равнобедренной трапеции ABCD диагональ AC является биссектрисой острого угла трапеции и образует со стороной CD угол 63{}^circ . Найдите углы трапеции.

Решение:

Пусть angle CAD =alpha , тогда angle CAB =alpha и angle BAD =2alpha , так как трапеция равнобедренная.

Сумма углов vartriangle ACD=3alpha +63{}^circ =180{}^circ , откуда
alpha =39{}^circ .
Итак, angle D=78{}^circ , аangle BCD=180{}^circ -78{}^circ =102{}^circ .

Ответ: 78{}^circ , 102{}^circ .

Задача 7.

В равнобедренной трапеции основания равны 10 м и 24 м, боковая сторона 25 м. Найдите высоту трапеции.

Решение:

В равнобедренной трапеции проведем высоты. Получим прямоугольник и два равных прямоугольных треугольника. Тогда основание каждого треугольника равно 7 и h^2={25}^2-7^2=left(25-7right)left(25+7right)=18cdot 32. Отсюда, h=sqrt{18cdot 32}=sqrt{9cdot 64}=3cdot 8=24.

Ответ: 24.

Задача 8.

Тупой угол равнобедренной трапеции равен {135}^circ , а высота, проведенная из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.

Решение:

Проведем две высоты. Они разделят трапецию на три части: прямоугольник и два равных прямоугольных треугольника с острым углом 45{}^circ .

Каждый треугольник равнобедренный, поэтому h = 1,4.

Нетрудно видеть, что верхнее основание трапеции равно 2, а нижнее — 4,8. Отсюда площадь трапеции равна displaystyle frac{2+4,8}{2}cdot 1,4=4,76.

Ответ: 4,76.

Задача 9.

Площадь трапеции равна 60м^2, а основания 8 м и 12 м. Найдите высоту трапеции.

Решение:

Так как площадь трапеции S=displaystyle frac{a+b}{2}cdot h, то 60=displaystyle frac{8+12}{2}cdot h, откуда h = 6.

Ответ: 6.

Задача 10.

В равнобедренной трапеции диагонали перпендикулярны и равны a. Найдите площадь трапеции.

Решение:

Проведем CE parallel BD и DE — продолжение AD.

Так как BCDE — параллелограмм, то CE = a.

По теореме 10 получим, что S_{ABCD}=S_{ACE}=displaystyle frac{1}{2}a^2.

Ответ: displaystyle frac{1}{2}a^2

Задач 11.

В трапеции ABCD с большим основанием AD диагональ AC перпендикулярна к боковой стороне CD и является биссектрисой угла A.

Найдите AD, если периметр трапеции равен 20, а угол D равен 60{}^circ .

Решение:

По условию задачи в прямоугольном vartriangle ACD

angle D =60{}^circ , следовательно, angle CAD =30{}^circ .

Так как AC — биссектриса, то angle CAB =30{}^circ , откуда angle DAB =60{}^circ , то есть, трапеция равнобедренная. angle BCA =angle CAD =30{}^circ как накрест лежащие, поэтому vartriangle ABC — равнобедренный.

Обозначим длины боковых сторон vartriangle ABC буквой x.

Тогда AB = BC = CD = x, и AD = 2x, так как в прямоугольном vartriangle ACD против угла в 30{}^circ лежит катет, равный половине гипотенузы.

Таким образом, периметр трапеции, равный 20, составляет 5x, отсюда

x = 4 и AD = 8.

Ответ: 8.

Задача 12.

В равнобедренной трапеции ABCD с острым углом 60{}^circ меньшее основание BC равно 2, а боковая сторона AB равна 10. Продолжения боковых сторон трапеции пересекаются в точке M. Во сколько раз площадь трапеции больше площади треугольника BCM?

Решение:

Нетрудно видеть, что vartriangle BCM равносторонний и BM = 2, тогда AM = 12 и vartriangle BCM подобен vartriangle ADM c коэффициентом k=12:2=6.

Пусть S_{BCM}=S_1, S_{ADM}=S_2, тогда

S_2=k^2cdot S_1=36{cdot S}_1.

Площадь трапеции будет равна

S_{ABCD}=S_2-S_1=36 S_1-S_1=35 S_1=35 S_{BCM}.

Ответ: 35.

Задача 13.

Сумма углов при одном из оснований трапеции равна 90{}^circ . Найдите длину отрезка, соединяющего середины оснований, если основания равны 6 и 10.

Решение:

Продолжим боковые стороны до пересечения в точке E и отметим точки F и G — середины оснований трапеции.

Так как сумма углов при основании трапеции равна 90{}^circ , то angle BEC=90{}^circ , поэтому EF и EG — медианы в прямоугольных треугольниках BEC и AED соответственно.

Известно, что медиана, проведенная к гипотенузе, равна ее половине, значит FG=EG-EF=AG-BF=5-3=2.

Ответ: 2.

Задача 14.

Найдите радиус окружности, вписанной в равнобочную трапецию, если средняя линия трапеции равна 10, а ее площадь 24.

Решение:

Так как площадь трапеции равна S=mh, а высота трапеции равна диаметру вписанной окружности, то есть h=2r, то 24=10cdot 2r, откуда r=1,2.

Ответ: 1,2.

Задача 15.

Периметр прямоугольной трапеции равен 32, а большая боковая сторона равна 10. Найдите радиус r вписанной в трапецию окружности.

Решение:

По свойствам описанной трапеции сумма ее боковых сторон равна сумме оснований, поэтому

AB+CD=32:2=16, откуда AB=16-10=6.

Сторона AB равна диаметру окружности, поэтому r=3.

Ответ: 3.

Задача 16.

Около окружности описана трапеция, сумма боковых сторон которой равна 40. Найдите длину ее средней линии.

Решение:

Длина средней линии трапеции равна полусумме оснований. Если трапеция описана вокруг окружности, то в ней сумма оснований равна сумме боковых сторон, поэтому

m=displaystyle frac{a+b}{2}=displaystyle frac{c+d}{2}=displaystyle frac{40}{2}=20.

Ответ: 20.

Задача 17.

В окружность вписана трапеция так, что диаметр окружности служит основанием трапеции, а вершины другого основания делят полуокружность на три равные части. Найдите тупые углы трапеции. Ответ выразите в градусах.

Решение:

Так как AD — диаметр окружности, то дуга ABCD равна 180{}^circ . Она делится на три равные части по 60{}^circ .

Вписанный угол D опирается на дугу ABC, которая равна 120{}^circ , отсюда angle ADC=60{}^circ и, стало быть, angle C=120{}^circ =angle B.

Ответ: 120.

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Трапеция и ее свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

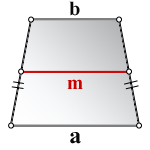
1. Формула средней линии равнобедренной трапеции через основания

средняя линия равнобедренной трапеции через основания

a — нижнее основание

b — верхнее основание

m — средняя линия

Формула средней линии, (m ):

Формула средней линии равнобедренной трапеции через основания

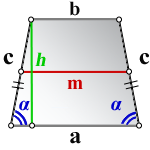
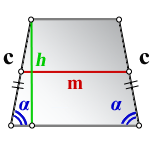
2. Формулы средней линии через основание, высоту и углы при нижнем основании

средняя линия через основание, высоту и углы при нижнем основании

a — нижнее основание

b — верхнее основание

c — боковая сторона

α — угол при нижнем осровании

h — высота трапеции

m — средняя линия

Формулы средней линии трапеции, (m ):

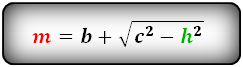
Формулы средней линии через основание, высоту и углы при нижнем основании

Формулы средней линии через основание, высоту и углы при нижнем основании

Формулы средней линии через основание, высоту и углы при нижнем основании

Формулы средней линии через основание, высоту и углы при нижнем основании

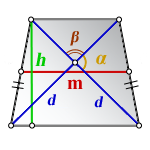
3. Формула средней линии трапеции через диагонали, высоту и угол между диагоналями

средняя линия трапеции через диагонали, высоту и угол между диагоналями

d — диагонали трапеции

α , β — углы между диагоналями

h — высота трапеции

m — средняя линия

Формула средней линии трапеции, (m ):

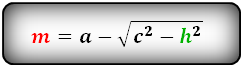
4. Формула средней линии трапеции через площадь и высоту

средняя линия трапеции через площадь и высоту

S — площадь трапеции

h — высота трапеции

α — угол при нижнем осровании

m — средняя линия

Формула средней линии трапеции, (m ):

Формула средней линии трапеции через площадь и высоту

Формулы площади произвольной трапеции

Формулы площади равнобедренной трапеции

Формула периметра трапеции

Все формулы по геометрии

Подробности

Опубликовано: 12 октября 2013

Обновлено: 13 августа 2021

Источник

Понравилась статья? Поделить с друзьями:
  • Как найти скрытый процесс в диспетчере задач
  • Как найти владельца по номеру дома
  • Как найти тханка far cry
  • Как исправить ошибку 001
  • Как происходило формирование новых органов власти составьте схему государственного устройства рсфср