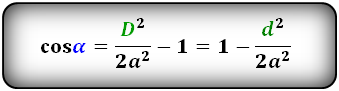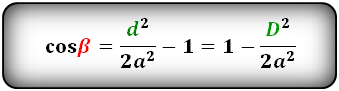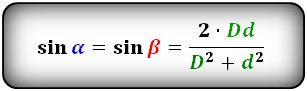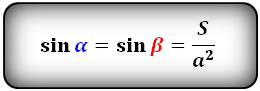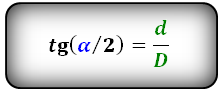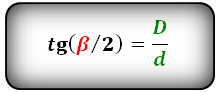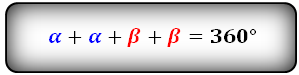Найти углы ромба, зная только его сторону, нельзя: существуют ромбы, имеющие разные углы, но одинаковые стороны. На пальцах: сделайте ромб из проволоки, «сплющите» его — он останется ромбом, стороны будут те же, углы изменятся.
Значит, чтобы найти углы ромба нужно знать что-то ещё (или что-то другое). Например, зная сторону и диагональ, найти угол можно по теореме косинусов: если x — сторона, d — диагональ, a — угол напротив диагонали, то условие теоремы косинуов — d^2 = x^2 + x^2 — 2 * x^2 * cos(a), из него следует a = arccos((2x^2 — d^2)/2x^2). (Я говорю «найти угол», а не «найти углы», потому что если мы знаем один угол, остальные находятся тривиально: если один угол равен а градусов, то угол напротив него тоже а, остальные два — по 180-а).
Есть и другие варианты: через сторону и площадь (пользуясь тем, что площадь — это квадрат стороны умножить на синус угла), через две диагонали (мы знаем, что диагонали в ромбе пересекаются под прямым углом и делятся точкой пересечения пополам — отсюда следует, что тангенс половины угла ромба равен отношению диагоналей, просто по определнию тангенса; зная сторону и диагональ, кстати, тоже можно искать угол примерно таким способом, вместо теоремы косинусов) и так далее.
Свойства ромба:
1. Ромб — частный случай параллелограмма
2. Противоположные стороны — параллельны
3. Все четыре стороны — равны
4. Диагонали пересекаются под прямым углом (90°)
5. Диагонали являются биссектрисами
a — сторона ромба
D — большая диагональ
d — меньшая диагональ
α — острый угол
β — тупой угол
Формулы косинуса углов через диагональ и сторону:
Формулы синуса углов через диагонали :
Формулы синуса углов через площадь S и сторону :
Формулы тангенса половинных углов через диагонали
Формулы соотношения острого и тупого углов:
Для определения величины угла в градусах или радианах, используем функции arccos или arcsin или arctg
Формулы площади ромба
Формула периметра ромба
Все формулы по геометрии
- Подробности
-
Опубликовано: 25 ноября 2011
-
Обновлено: 13 августа 2021
Вася Иванов
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Известно, что противоположные углы ромба равны, а соседние углы дополняют друг друга до 180º. Этот калькулятор поможет быстро определить углы ромба, если известны его диагонали. Для этого в меню выберите расчет через диагонали ромба, после чего заполните соответствующие ячейки и нажмите на кнопку “Рассчитать”.
В итоге станут известны не только тупой и острый углы ромба, но и периметр, высота, стороны, площадь ромба вместе с развернутыми формулами всех вычислений.
Добавьте калькулятор в закладки, чтобы иметь шпаргалку по геометрии всегда под рукой.
Рассчитать если известны: *
Введите данные:
Острый угол в градусах (α)
Тупой угол в градусах (β)
Вертикальная диагональ (d1)
Горизонтальная диагональ (d2)
Округление:
* — обязательно заполнить
Как найти угол ромба
Ромб образуется из квадрата при растягивании фигуры за вершины, расположенные на одной диагонали. Два угла становятся меньше прямых. Два других угла увеличиваются, превращаясь в тупые.
Сумма четырех внутренних углов ромба равна 360°, как у любого четырехугольника. Противоположные углы ромба равны, при этом всегда в одной паре равных углов — углы острые, в другой — тупые.Два угла, прилегающие к одной стороне в сумме составляют развернутый угол. Ромбы с одинаковым размером стороны могут внешне очень сильно отличаться друг от друга.Это различие объясняется разной величиной внутренних углов. Следовательно, для нахождения угла ромба недостаточно знать только его сторону.
Достаточным для определения величины углов ромба является знание диагоналей фигуры.После проведения в ромбе обеих диагоналей ромб будет разбит на четыре треугольника. Диагонали ромба расположены под прямым углом, следовательно, полученныетреугольники являются прямоугольными. Ромб — симметричная фигура, его диагонали являются одновременно осями симметрии, поэтому все внутренние треугольникиравны. Острые углы треугольников, образованных диагоналями ромба, равны половине углов ромба, которые нужно найти.
Тангенс острого угла прямоугольного треугольника равен отношению катетов, противолежащего к прилежащему. Половина каждой диагонали ромба является катетом прямоугольного треугольника. Если большую и малую диагонали ромба обозначить d₁ и d₂соответственно, а углы ромба — А (острый) и В (тупой), то из соотношения сторон в прямоугольных треугольниках внутри ромба следует: tg (A/2)=(d₂/2)/(d₁/2)=d₂/d₁,tg(B/2)=(d₁/2)/(d₂/2)=d₁/d₂.
По формуле двойного углаtg (2α) = 2/(сtg α — tg α) найдитетангенсы углов ромба: tg A = 2/((d₁/d₂)-(d₂/d₁)) и tg B =2/((d₂/d₁)-(d₁/d₂)). По тригонометрическим таблицам найдите углы, соответствующие рассчитанным значениям их тангенсов.