Как найти углы треугольника зная координаты точек - Исправление недочетов и поиск решений вместе с Examum.ru

Как найти угол треугольника по его координатам

Если известны координаты всех трех вершин треугольника, можно найти и его углы. Координаты точки в трехмерном пространстве — x,y и z. Однако через три точки, которые являются вершинами треугольника, всегда можно провести плоскость, поэтому в этой задаче удобнее рассматривать только две координаты точек — x и y, считая координату z для всех точек одинаковой.

Вам понадобится

Координаты треугольника

Инструкция

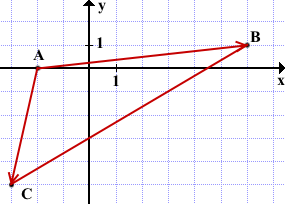
Пусть точка A треугольника ABC имеет координаты x1, y1, точка B этого треугольника — координаты x2, y2, а точка C — координаты x3, y3. Что представляют из себя координаты x и y вершин треугольника. В декартовой системе координат с перпендикулярными друг другу осями X и Y от начала координат можно провести радиус-векторы ко всем трем точкам. Проекции радиус-векторов на координатные оси и будут давать координаты точек.

Пусть тогда r1 — радиус вектор точки A, r2 — радиус-вектор точки B, а r3 — радиус-вектор точки C.
Очевидно, что длина стороны AB будет равна |r1-r2|, длина стороны AC = |r1-r3|, a BC = |r2-r3|.
Следовательно, AB = sqrt(((x1-x2)^2)+((y1-y2)^2)), AC = sqrt(((x1-x3)^2)+((y1-y3)^2)), BC = sqrt(((x2-x3)^2)+((y2-y3)^2)).

Углы треугольника ABC можно найти из теоремы косинусов. Теорему косинусов можно записать в следующем виде: BC^2 = (AB^2)+(AC^2) — 2AB*AC*cos(BAC). Отсюда, cos(BAC) = ((AB^2)+(AC^2)-(BC^2))/2*AB*AC. После подстановки в это выражения координаты, получится: сos(BAC) = (((x1-x2)^2)+((y1-y2)^2)+((x1-x3)^2)+((y1-y3)^2)-((x2-x3)^2)-((y2-y3)^2))/(2*sqrt(((x1-x2)^2)+((y1-y2)^2))*sqrt(((x1-x3)^2)+((y1-y3)^2)))

Источники:

как найти координаты третьей вершины
Медианы, биссектрисы и высоты треугольника

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Угол между векторами

Определение

Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.

Угол между векторами

На изображении это α, который также можно обозначить следующим образом:

(left(widehat{overrightarrow a;overrightarrow b}right))

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как и любой другой угол, векторный может быть представлен в нескольких вариациях.

Острый:

Острый угол между векторами

Тупой:

Тупой угол между векторами

Прямой:

Прямой угол

С величиной (0^circ) (то есть, векторы сонаправлены):

0 градусов

С величиной (180^circ) (векторы направлены в противоположные стороны):

180 градусов

Нахождение угла между векторами

Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.

Определение

Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.

Формула скалярного произведения:

(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))

Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.

В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})

Расчет угла, если вектор задан координатами

В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:

Если же координаты находятся в трехмерном пространстве и заданы в виде:

(overrightarrow a=left(a_x;a_y;a_zright))

( overrightarrow b=left(b_x;b_y;b_zright))

то формула принимает такой вид:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})

Расчет угла, если заданы три точки в прямоугольной системе координат

В этом случае проще будет разобраться с объяснениями сразу на примере.

Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).

Решение

Для начала найдем их координаты по известным координатам заданных точек:

(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))

(overrightarrow{BC}=(6-2, -1-1)=(4,-2))

После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:

(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})

Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)

Примеры решения задач

Для наглядности, взглянем на примеры решения задач по данной теме.

Задача 1

Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.

Решение

Применим формулу:

( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})

Подставим известные значения:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)

Далее найдем угол между данными векторами:

(arccosleft(-frac12right)=frac{3pi}4)

Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)

Задача 2

В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.

Решение

Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:

Подставляем значения и получаем:

(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})

Теперь находим угол α:

(alpha=arccosleft(frac2{sqrt2}right)=45^circ)

Ответ: (45^circ).

Задача 3

Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.

Решение

Для расчета используем формулу:

Подставим известные значения и получим:

(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})

Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})

Источник

Как найти угол треугольника по его координатам

Пусть точка A ABC имеет координаты x1, y1, точка B этого треугольника — координаты x2, y2, а точка C — координаты x3, y3. Что представляют из себя координаты x и y вершин треугольника. В декартовой системе координат с перпендикулярными друг другу осями X и Y от начала координат можно провести радиус-векторы ко всем трем точкам. Проекции радиус-векторов на координатные оси и будут давать координаты точек.

Источник

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Примеры решений по аналитической геометрии на плоскости

В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.

Решения задач о треугольнике онлайн

Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.

Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.

Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.

Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.

Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.

Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.

Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, — 4)$, $В(3, 0)$ и $С(0, 6)$.

Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.

Найти косинусы углов треугольника

Мы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.

Рассмотрим, как найти косинусы углов треугольника по его вершинам.

1) Найти косинусы углов треугольника ABC;

2) Определить вид треугольника.

1) Угол A образован векторами

(Чертёж не обязательно делать на координатной плоскости. Достаточно выполнить его схематически, для упрощения понимания, какой угол какими векторами образован).

$[cos A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}}.]$

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A ),]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A ),]$

Поскольку скалярное произведение меньше нуля, угол, образованный данными векторами, тупой. Значит треугольник ABC — тупоугольный.

$[left| {overrightarrow {AB} } right| = sqrt {8^2 + 1^2 } = sqrt {65} ,]$

$[left| {overrightarrow {AC} } right| = sqrt {( - 1)^2 + ( - 5)^2 } = sqrt {26} .]$

$[cos A = frac{{ - 13}}{{sqrt {65} cdot sqrt {26} }} = frac{{ - 13}}{{sqrt {5 cdot 13 cdot 2 cdot 13} }} = ]$

$[= frac{{ - 13}}{{13sqrt {10} }} = - frac{1}{{sqrt {10} }} = - frac{{sqrt {10} }}{{10}}.]$

2) Угол B образован векторами

$[cos B = frac{{overrightarrow {BA} cdot overrightarrow {BC} }}{{left| {overrightarrow {BA} } right| cdot left| {overrightarrow {BC} } right|}}.]$

— противоположные векторы, то их координаты отличаются только знаками и векторы имеют одинаковую длину:

Как найти косинус внутреннего угла при вершине В?

Вычислим стороны треугольника АВС, используя формулу определения расстояния между точками в прямоугольной декартовой системе координат в пространстве.

Затем, применив теорему косинусов, найдем искомый угол.

Вот таким образом у меня получилось, если не ошибся в арифметике

Найти косинус угла АВС можно по формуле для расчёта угла между двумя векторами.

Зная координаты вершин А(2;-2;-2), В(2;2;-1) и С(3;1;-2), находим вектора АВ = , СВ = . Для этого мы использовали формулу вида:

Источник