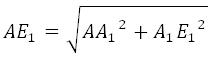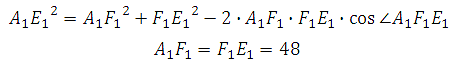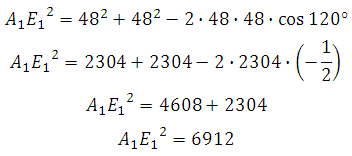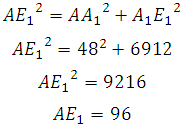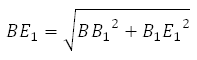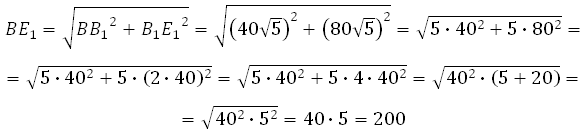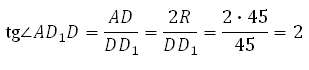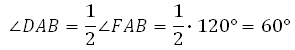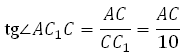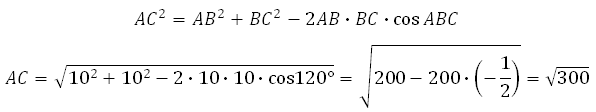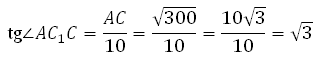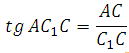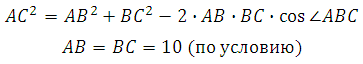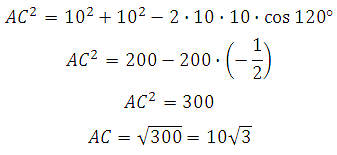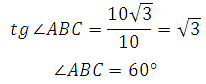Конспект урока по теме «Нахождение углов в
призме»
Тема. Нахождение углов в призме
Цель: повторить и обобщить материал на
нахождение углов между прямыми и плоскостями при решении задач по теме
«Призма».
Задачи:
Образовательные – научить использовать
методы решения задач, применяемые для куба, на призме.
Развивающие – развить
мышления через формирование умений анализировать, сравнивать; формирование
логического, абстрактного мышления;
Воспитательные – воспитать
самостоятельность, настойчивость, положительное эмоциональное отношение к
математике.
Тип урока – урок повторения.
Оборудование: доска, карточка с
заданиями.
Структура урока:
1.
Организационный
момент (2)
2.
Актуализация
знаний (10)
3.
Решение
задач (25)
4.
Информация
о домашнем задании(3)
Ход урока.
I Организационный момент
Здравствуйте! Садитесь! На
прошлых уроках вы вспомнили, как находить углы и расстояния между различными
элементами куба. Сегодня мы вспомним, как находит углы в призме.
II Актуализация опорных знаний
Для актуализации учащимся раздаются
карточки с заданиями (таблица 9).
Карточка с заданием
|
Укажите искомый угол между |
||
|
скрещивающимися прямыми |
прямой |
двумя плоскостями |
|
|
|
|
III Решение задач
Задание в группах
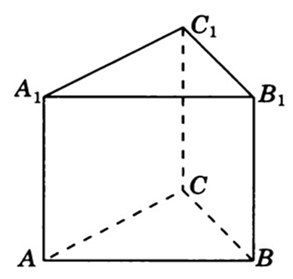
Задача 1. В правильной треугольной призме боковое ребро равно
, а сторона основания
. Найти косинус угла между плоскостями
и
.
Задача 2. В
правильной треугольной призме , все ребра которой
равны 1, найти угол между прямой и плоскостью
.
Задача 3. Дан
прямоугольный параллелепипед . Его диагональ
составляет с ребром AD угол
, а с ребром DC угол
. Найти угол между двумя прямыми
и
.
IV Информация о домашнем задании
(таблица 11)
Домашнее задание
На сайте уже были рассмотрены некоторые типы задач по стереометрии, которые входят в единый банк заданий экзамена по математике. Например, задания про составные многогранники.
Призма называется правильной если её боковые перпендикулярны основаниям и в основаниях лежит правильный многоугольник. То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.
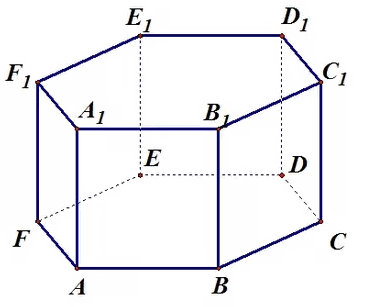
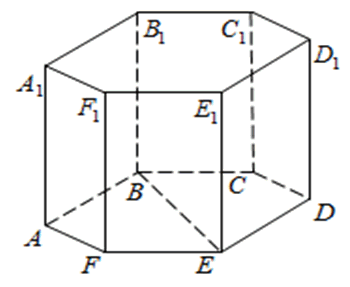
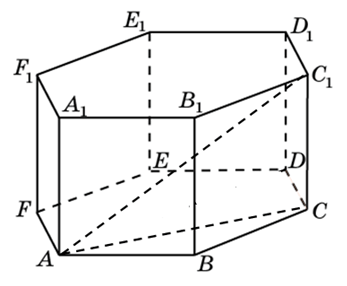
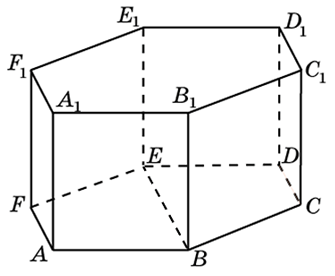
Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.
В этой статье для вас задачи на решение призмы, в основании которой лежит правильный шестиугольник. Особенностей и сложностей в решении нет никаких. В чём суть? Дана правильная шестиугольная призма, требуется вычислить расстояние между двумя вершинами или найти заданный угол. Задачи на самом деле простые, в итоге решение сводится к нахождению элемента в прямоугольном треугольнике.
Используется теорема Пифагора и теорема косинусов. Необходимо знание определений тригонометрических функций в прямоугольном треугольнике.
Обязательно посмотрите информацию о правильном шестиугольнике в этой статье (пункт 6). Ещё вам пригодится навык извлечения квадратного корня их большого числа. Можете посмотреть статью на решение многогранников, там тоже вычисляли расстояние между вершинами и углы.
Кратко: что представляет собой правильный шестиугольник?
Известно, что в правильном шестиугольнике стороны равны. Кроме этого, углы между сторонами тоже равны.
*Противолежащие стороны параллельны.
Дополнительная информация
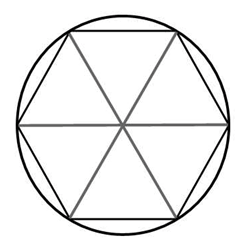
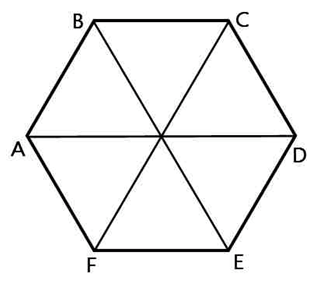
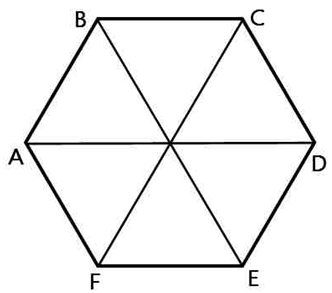
Радиус окружности описанной около правильного шестиугольника равен его стороне. *Это подтверждается очень просто: если мы соединим противоположные вершины шестиугольника, то получим шесть равных равносторонних треугольников. Почему равносторонних?
У каждого треугольника угол при его вершине лежащей в центре равен 600 (360:6=60). Так как у треугольника две стороны имеющие общую вершину в центре равны (это радиусы описанной окружности), то каждый угол при основании такого равнобедренного треугольника так же равен 60 градусам.
То есть правильный шестиугольник, образно говоря, состоит как бы из шести равных равносторонних треугольников.
Какой полезный для решения задач факт ещё следует отметить? Угол при вершине шестиугольника (угол между его соседними сторонами) равен 120 градусам.
*Умышленно не коснулись формул правильного N-угольника. Данные формулы мы подробно рассмотрим в будущем, здесь они просто не нужны.
Рассмотрим задачи:
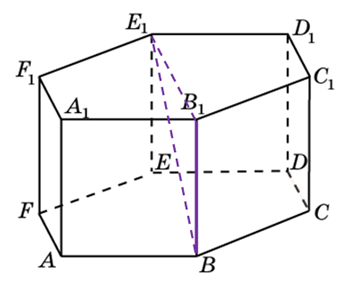
272533. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 48. Найдите расстояние между точками A и E1.
Рассмотрим прямоугольный треугольник AA1E1. По теореме Пифагора:
*Угол между сторонами правильного шестиугольника равен 120 градусам.
Отрезок АЕ1 является гипотенузой, АА1 и А1Е1 катеты. Ребро АА1 нам известно. Катет А1Е1 мы можем найти используя используя теорему косинусов.
Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон без удвоенного произведения этих сторон на косинус угла между ними.
Следовательно
По теореме Пифагора:
Ответ: 96
*Обратите внимание, что 48 возводить в квадрат совсем не обязательно.
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 35. Найдите расстояние между точками B и E.
Рассмотрим правильный шестиугольник:
Сказано, что все рёбра равны 35, то есть сторона шестиугольника лежащего в основании равна 35. А так же, как уже сказано, радиус описанной около него окружности равен этому же числу.
Таким образом,
Ответ: 70
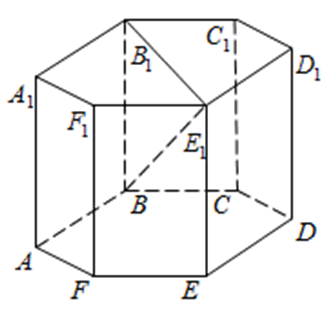
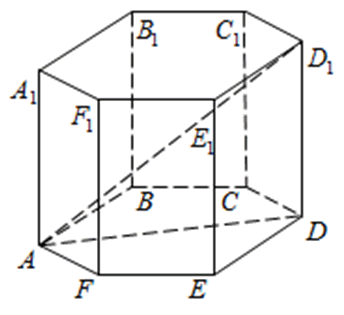
273353. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны сорока корням из пяти. Найдите расстояние между точками B и E1.
Рассмотрим прямоугольный треугольник BB1E1. По теореме Пифагора:
Отрезок B1E1 равен двум радиусам описанной около правильного шестиугольника окружности, а её радиус равен стороне шестиугольника, то есть
Таким образом,
Ответ: 200
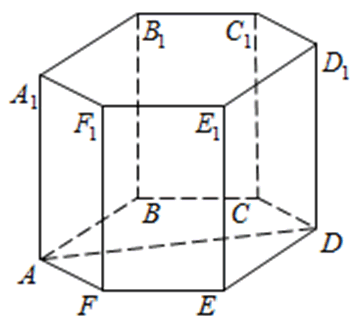
273683. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 45. Найдите тангенс угла AD1D.
Рассмотрим прямоугольный треугольник ADD1, в котором AD равно диаметру окружности, описанной вокруг основания. Известно, что радиус окружности, описанной вокруг правильного шестиугольника равен его стороне.
Таким образом,
Ответ: 2
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 23. Найдите угол DAB. Ответ дайте в градусах.
Рассмотрим правильный шестиугольник:
В нём углы между сторонами равны 120°. Значит,
Сама длина ребра не имеет значения, на величину угла она не влияет.
Ответ: 60
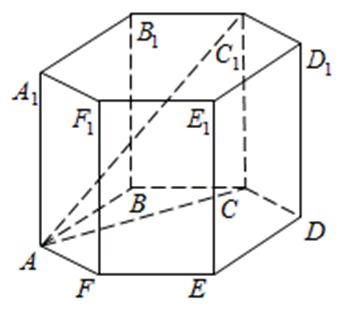
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим прямоугольный треугольник AC1C:
Найдём AC. В правильном шестиугольнике углы между его сторонами равны 120 градусам, тогда по теореме косинусов для треугольника АВС :
Таким образом,
Значит, угол AC1C равен 60 градусам.
Ответ: 60
274453. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 10. Найдите угол AC1C. Ответ дайте в градусах.
Рассмотрим треугольник AС1С, он прямоугольный. Вычислим тангенс указанного в условии угла и определим угол. Известно, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему, то есть
Катет С1С = 10. Отрезок АС вычислим по теореме косинусов (это мы уже делали в первой задаче, запишем ещё раз):
В правильном шестиугольнике углы при вершинах равны 120 градусам, то есть
Следовательно
Таким образом:
Ответ: 60
245364. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками А и Е1.
Посмотреть решение
245365. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите расстояние между точками В и Е.
Посмотреть решение
245366. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1все ребра равны корню из пяти. Найдите расстояние между точками В и Е1.
Посмотреть решение
245367. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите тангенс угла AD1D.
Посмотреть решение
245368. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах.
Посмотреть решение
245369. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра равны 1. Найдите угол AC1C. Ответ дайте в градусах.
Посмотреть решение
На этом всё! Успеха Вам!
В состав ЕГЭ включены и другие задачи по стереометрии, и они довольно разнообразны. Обязательно будем их рассматривать, не пропустите! Успехов вам!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Содержание
- Как найти угол бета в призме
- Угол между прямыми в призме
- ЕГЭ, С2 (№16). Угол между плоскостями в призме
- Видеоразбор
Как найти угол бета в призме
2017-04-30 
Луч света падает на трехгранную стеклянную призму под углом $alpha$. Показатель преломления стекла — $n$. Преломляющий угол призмы — $phi$. Под каким углом луч выйдет из призмы и каков угол его отклонения от первоначального направления?
NA — падающий луч (рис.); $AB perp PQ: AC$ — преломленный в призме луч; $angle BAC = beta$ — угол преломления; $BC perp QR; angle ACB = gamma; psi$ — искомый угол выхода луча из призмы; $angle CDM = 0$ — угол отклонения луча. Проведенное построение показывает, что призма отклоняет падающий на нее луч к основанию. Запишем закон преломления в точках А и С.
Так как $AB perp PQ$ и $BC perp QR$, то $angle CBL = angle PQR = phi. angle CBL$ — внешний угол $Delta ABC$, поэтому он равен сумме двух внутренних углов, с ним не смежных.
$angle CBL = angle BAC + angle ACB$ или $phi = beta + gamma$ (3).
Из (1): $sin beta = frac< sin alpha> Rightarrow beta = arcsin left ( frac< sin alpha> right )$.
Из (3): $gamma = phi — beta = phi — arcsin left ( frac< sin alpha> right )$.
Из (2): $sin psi = n sin gamma = n sin left ( phi — arcsin left ( frac< sin alpha> right ) right ) = n left ( sin phi cos arcsin left ( frac< sin alpha> right ) — cos phi frac< sin alpha> right )$;
Из тригонометрии известно, что $cos arcsin x = sqrt<1 — x^<2>>$, поэтому $sin psi = n left ( sin phi sqrt <1 — frac< sin^<2>alpha>>> — cos phi frac< sin alpha> right ) = sin phi sqrt < n^<2>— sin^ <2>alpha> — cos phi sin alpha$. Следовательно, $psi = arcsin ( sin phi sqrt < n^<2>— sin^ <2>alpha> — cos phi sin alpha)$ (4).
Отметим, что $angle DAB = alpha$ (вертикальные углы) и $angle DCB = psi$. Поэтому $angle DAC = angle DAB — beta = alpha — beta$, а $angle ACD = angle DCB — gamma = psi — gamma$.
$theta$ — внешний угол $Delta ADC$, поэтому $theta = angle DAC + angle ACD = ( alpha — beta) + ( psi — gamma) = ( alpha + psi ) — ( beta + gamma)$
Но, как уже доказывалось, $beta + gamma = phi$, следовательно $theta = ( alpha + psi) — phi$ (5). Отметим, что угол $psi$ вычисляется по формуле (4).
При малых преломляющих углах $phi$ и малых углах падения $alpha$ формулу (5) можно существенно упростить. Из (1): $sin alpha = n sin beta$. Так как $alpha$ и $beta$ — малы, то $alpha = n beta$. Из (2): $sin psi = n sin gamma$. При малых $alpha$ и $phi$ углы $psi$ и $gamma$ также малы, поэтому $psi = n gamma$. Формула принимает вид:
$theta = (n beta + n gamma) — phi = n( beta + gamma) — phi = n phi — phi = (n — 1) phi$.
Источник
Угол между прямыми в призме
Угол между прямыми в призме. Для вас очередной материал – мы рассмотрим пару задач с призмами. Требуется определить угол между прямыми проходящими через указанные вершины призмы. Дело в том, что эти прямые не лежат в одной плоскости. Такие прямые называют скрещивающимися.
Если вы с ними уже знакомы, то задачки решите сразу сходу после построения эскиза без всяких вычислений. Если нет, то посмотрите соответствующую теорию, можете посмотреть информацию здесь , материал подан достаточно наглядно.
Принцип прост – необходимо одну из прямых переместить до пересечения со второй параллельным переносом. Либо установить — имеется ли параллельная ей прямая в одной плоскости со второй прямой. Рассмотрим задачи:
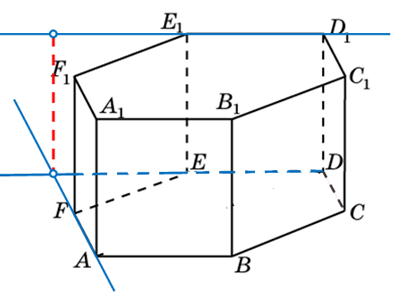
316553. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 все ребра которой равны 8, найдите угол между прямыми FA и D1Е1. Ответ дайте в градусах.
Построим прямые, переместим параллельным переносом прямую D1Е1 до пересечения с прямой AF. Полученная прямая будет проходить через DE:
Зная свойства правильного шестиугольника, а именно, то что углы при его вершинах равны 120 градусам, мы уже можем записать ответ. Угол между указанными прямыми равен 60 0 . Если посмотреть на призму сверху, то эскиз будет выглядеть так:
*Как видим, на самом деле, чему равна длина ребра не имеет значения.
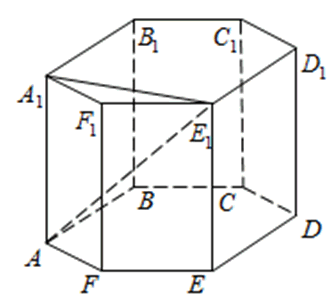
316558. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 3, найдите угол между прямыми AA1и BC1. Ответ дайте в градусах.
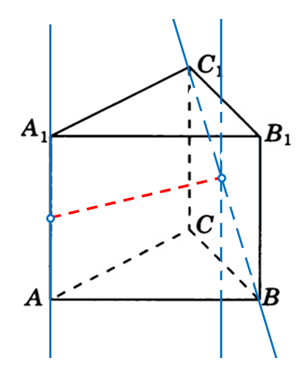
Построим указанные прямые и параллельным переносом «передвинем» прямую AA1 до грани BCC1B1 через которую проходит BC1:
Так как в условии сказано, что все рёбра равны 3, то это значит что грань BCC1B1 является квадратом. Прямая BC1 является диагональю этого квадрата и она пересекает все прямые параллельные боковым рёбрам под углом 45 градусов. Наглядно это можно увидеть на проекции призмы:
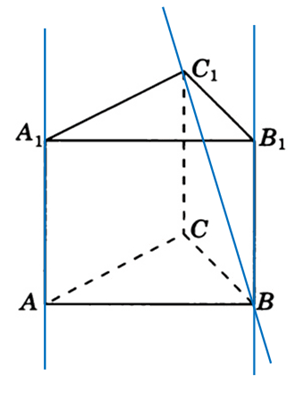
*Небольшая оговорка. В обеих задачах мы перемещали прямые как бы «стягивая» их по соединяющему их перпендикуляру (обозначен красным пунктиром). Необязательно это делать именно так. Важно, чтобы одна из прямых была перемещена до пересечения с другой именно параллельным сдвигом. Во второй задаче это можно было сделать и так:
На этом закончим. Так что если встретите скрещивающиеся прямые на ЕГЭ в задаче кратким ответом, не пугайтесь, решаются они устно. Важно понимать, каким образом переместить прямую до пересечения с другой. А уж угол найти, как говорится, это дело техники.
Источник
ЕГЭ, С2 (№16). Угол между плоскостями в призме
Видеоразбор
Задача С2 (в новом формате ЕГЭ по математике – «Задание №14»)
В правильной четырёхугольной призме стороны основания равны
, а боковые ребра равны
. На ребре
отмечена точка
так, что
. Найдите угол между плоскостями
и
.
Похожее задание для самостоятельной проработки:
В правильной четырёхугольной призме стороны основания равны
, а боковые рёбра равны
. На ребре
отмечена точка
так, что
. Найдите угол между плоскостями
и
.
Ответ:
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Источник
В
данной теме разберём решение задач на ход лучей в треугольной призме.
Задача
1.
Луч света падает на преломляющую грань призмы под углом 30º и выходит из
неё под углом 25º. При этом угол отклонения луча составляет 10º.
Постройте ход лучей в призме и найдите её преломляющий угол.
|
ДАНО: |
РЕШЕНИЕ Угол Тогда |
|
|
Задача
2.
Луч света падает на преломляющую грань призмы под углом 1º. Найдите
показатель преломления материала, из которого сделана призма, если преломляющий
угол призмы равен 30º, а угол отклонения луча составляет 18º.
|
ДАНО: |
РЕШЕНИЕ Угол Тогда |
|
|
Задача
3.
Луч света падает на преломляющую грань призмы таким образом, что преломлённый
луч внутри призмы распространяется в направлении, параллельном основанию
призмы. Известно, что преломляющий угол призмы равен 50º, а угол падения
равен 35º. Найдите показатель преломления материала, из которого сделана
призма.
|
ДАНО: |
РЕШЕНИЕ Т.к. Из Тогда Закон |
|
|
Задача
4.
Луч света вошёл в призму с показателем преломления 2,4 и не вышел из неё.
Найдите минимальный угол падения луча на преломляющую грань, при котором это
возможно, учитывая то, перпендикуляры к преломляющим граням призмы пересекаются
под углом, равным сумме преломляющего угла призмы и угла отклонения луча.
|
ДАНО: |
РЕШЕНИЕ Предельный Т.к. Угол Тогда Закон |
|
|
Как найти угол между плоскостями?
Найти угол между плоскостями можно двумя способами: геометрическим и алгебраическим.
Геометрический способ
При геометрическом способе нужно сначала построить угол двугранного угла, а потом искать этот линейный угол с помощью знаний из планиметрии.
Алгебраический способ
Алгебраический способ – это применение метода координат – там есть формула для нахождения угла между плоскостями.
Вот такая:
( displaystyle cos gamma =frac{{{A}_{1}}{{A}_{2}}+{{B}_{1}}{{B}_{2}}+{{C}_{1}}{{C}_{2}}}{sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}})
Здесь ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}) — коэффициенты уравнений плоскостей ( displaystyle alpha ) и ( displaystyle beta ) соответственно.
Подробнее про уравнение плоскости ты можешь прочитать в статье «Расстояние от точки до плоскости»!
( displaystyle alpha ): ( displaystyle {{A}_{1}}x+{{B}_{1}}y+{{C}_{1}}z+D=0)
( displaystyle beta ): ( displaystyle {{A}_{2}}x+{{B}_{2}}y+{{C}_{2}}z+D=0).
Какой же способ лучше? Зависит от задачи.
Если нужно найти, скажем, двугранный угол при основании правильной , то проще использовать геометрический способ.
А если линейный угол двугранного угла никак не хочет проходить ни через какие удобные точки, то можно использовать метод координат как палочку выручалочку.
Но тогда нужно очень твёрдо знать формулы и не делать арифметических ошибок при многочисленных подсчётах – ведь придётся искать ( displaystyle {{A}_{1}},{{B}_{1}},{{C}_{1}},{{A}_{2}},{{B}_{2}},{{C}_{2}}), а потом ещё и ( displaystyle cos gamma ).
Давай разберём несложную задачу для примера. Мы применим оба метода к одной и той же задаче.