Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
и
где q1=(m1, p1) направляющий вектор прямой L1, а q2=(m2, p2) направляющий вектор прямой L2.
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
Из определения скалярного произведения:
где |q1| и |q2| модули направляющих векторов q1 и q2 соответственно, φ -угол между векторами q1 и q2.
Из выражения (1.3) получим:
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
и
Решение. Прямая (1.5) имеет направляющий вектор q1=(m1, p1)=(3, 4), а прямая (1.6) − q2=(m2, p2)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m1, p1, m2, p2 в (1.4):
Упростим и решим:
Найдем угол φ
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
Ответ.
Угол между прямыми равен:
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
Сделаем преобразования с выражением (1.7):
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
Пример 2. Определить, параллельны ли прямые
и
Решение. Прямая (1.10) имеет направляющий вектор q1=(m1, p1)=(3, 3), а прямая (1.11) − q2=(m2, p2)=(−2, −2). Тогда
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
и
Решение. Прямая (1.14) имеет направляющий вектор q1=(m1, p1)=(3, 1), а прямая (1.15) − q2=(m2, p2)=(−2, 6). Тогда
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
и
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
Из определения скалярного произведения двух векторов, имеем:
где |n1| и |n2| модули нормальных векторов n1 и n2 соответственно, φ -угол между векторами n1 и n2.
Из уравнения (19) получим
Пример 4. Найти угол между прямыми
и
Решение. Прямая (1.21) имеет нормальный вектор n1=(A1, B1)=(5, −2), а прямая (1.22) − n2=(A2, B2)=(1, 3). Задача определения угла между прямыми L1 и L2 сводится к определению угла между векторами n1 и n2. Из определения скалярного произведения векторов имеем: (n1,n2)=|n1||n2|cosφ. Тогда
Подставляя значения A1, B1, A2, B2 в (1.23), получим:
Упростим и решим:
Найдем угол φ:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
и
Решение. Прямая (1.26) имеет нормальный вектор n1=(A1, B1)=(4, 2), а прямая (1.27) − n2=(A2, B2)=(2, 1). Тогда подставляя значения A1, B1, A2, B2 в (1.24), получим
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
и
Решение. Прямая (1.29) имеет нормальный вектор n1=(A1, B1)=(4, −1), а прямая (1.30) − n2=(A2, B2)=(2, 8). Тогда подставляя значения A1, B1, A2, B2 в (28), получим
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
и
где q1=(m1, p1, l1) направляющий вектор прямой L1, а q2=(m2, p2, l2) направляющий вектор прямой L2.
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
Из определения скалярного произведения:
где |q1| и |q2| модули направляющих векторов q1 и q2 соответственно, φ -угол между векторами q1 и q2.
Из выражения (2.3) получим:
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
и
Решение. Прямая (2.5) имеет направляющий вектор q1=(m1, p1, l1)=(1, 1, 3), а прямая (2.6) − q2=(m2, p2, l2)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m1, p1, l1, m2, p2, l2 в (2.4):
Упростим и решим:
Найдем угол φ
Ответ.
Угол между прямыми равен:
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
и
Решение. Прямая (2.9) имеет направляющий вектор q1=(m1, p1, l1)=(3, 2, 4), а прямая (2.10) − q2=(m2, p2, l2)=(6, 4, 8). Тогда
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
и
Решение. Прямая (2.9) имеет направляющий вектор q1=(m1, p1, l1)=(1, 2, 0), а прямая (2.10) − q2=(m2, p2, l2)=(2, 4, 0). Подставляя значения m1, p1, l1, m2, p2, l2 в (2.8), получим
Выражение (2.13) нужно понимать так:
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
и
Решение. Прямая (2.16) имеет направляющий вектор q1=(m1, p1, l1)=(3, 2, 1), а прямая (2.17) − q2=(m2, p2, l2)=(4, −6, 0). Тогда
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Определение угла между прямыми
Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.
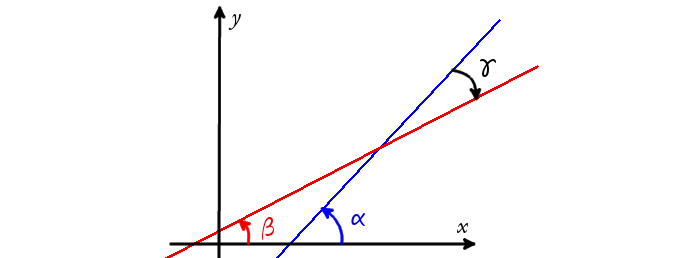
Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α — β
tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k1 — k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых
Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x — x0 l = y — y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых
Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; —k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 — k21 + k1·k2
=
2 — (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x — 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ =
k1 — k21 + k1·k2
=
-23 — 431 + (-23)·43
=
-631 — 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x — x0 l = y — y0m = z — z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t — 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x — 23
=
y4
=
z — 35
и —
x — 22
= 1 — 3y =
3z — 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
—x — 22 = x — 2-2
1 — 3y = 1 + y-1/3 = y — 1/3-1/3
3z — 52 = z — 5/32/3
Получено уравнение второй прямой в канонической форме
x — 2-2 = y — 1/3-1/3 = z — 5/32/3
{-2; -13; 23} — направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
Определение угла между скрещивающимися прямыми
Пересечение двух линий на плоскости говорит о наличии у них одной общей точки. Она же является центром их пересечения и делит их на лучи.
Лучи формируют четыре угла, которые являются неразвернутыми. Зная о размере одного из них, можно вычислить значение и остальных. Точно можно утверждать, что если один из них – прямоугольный, то остальные три равнозначны ему, а линии будут перпендикулярными.
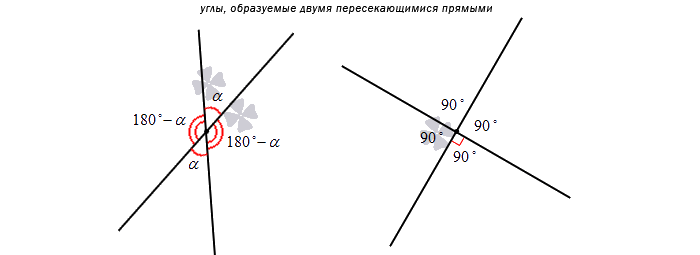
Рис. 1 Графическое отображение пересечения прямых
Как найти угол между скрещивающимися прямыми
Для определения угла между двумя скрещивающимися линиями можно воспользоваться специальным онлайн-калькулятором или применить традиционный математический алгоритм для вычислений.
Предположим, что две бесконечные линии задаются уравнениями общего вида:
A1 + B1 + C1 = 0
A2 + B2 + C2 = 0
Искомое значение следует обозначить как φ. Численная величина угла измеряется в градусах от 0 до 90°, т. е. угол будет острым или прямоугольным. Необходимо ввести еще одно понятие– угол ψ между нормальными векторами данных прямых:
Если он меньше, либо равен 90°, то непосредственно сам искомый угол будет соответствовать его градусной мере. В случае когда ψ больше 90°, для вычисления φ необходимо применить известную формулу:
φ = 1800 — ψ.
Для обоих вариантов достоверно утверждение, что cos φ = lcos ψl. Выполнив необходимые вычисления, можно рассчитать искомое значение:
Если по условию задачи существует некий прямоугольный треугольник с известными сторонами, расположенными на двух прямых, то для вычисления угла между этими прямыми необходимо знать синус, тангенс и косинус искомого угла.
Для нахождения значения синуса угла, образованного в результате пересечения двух прямых, вычисляют модуль косинуса этого угла, образованного направляющими векторами данных прямых.
Пример решения задачи
На школьных уроках геометрии для решения в классе часто предлагается следующий вид задач по поиску угла между двумя прямыми.
Ниже приведем алгоритм решения задачи, при которой бесконечные линии на плоскости заданы уравнениями общего вида, в которых присутствует угловой коэффициент.
Обозначим прямые как (L1) и (L2). Каждая из них задается уравнением следующего вида:
А1х + В1у + С1 = 0;
А2х + В2у + С2 = 0;
Зная, что нормальные вектора каждой из них имеют вид:
Суть задачи сводится к вычислению угла φ, образованного нормальными векторами.
Используем определение скалярного произведения векторов:
и координатное выражение их длин, а также их скалярное произведение:
В практических задачах по математике часто требуется найти не сам угол между пресекающимися прямыми, а составить уравнение их всех, при условии, что прямые пересекаются между собой.
Так, если прямые заданы уравнениями общего вида с коэффициентами, то
Последнее равенство часто называют уравнением биссектрис углов, образованных в результате пересечения прямых. Понятие «биссектриса» в геометрии — это некое геометрическое место точек, которые удалены на одинаковое расстояние от сторон угла.
Если прямые задаются уравнениями, включающими угловой коэффициент, который определяется тангенсом угла, найти значение углов, образованных при их пересечении, достаточно просто:
Рис. 2 Углы, образованные пересечением двух прямых на плоскости
tan α = k1;
tan β = k2;
где k1 и k2 – те самые угловые коэффициенты.
Следовательно, чтобы вычислить значение γ, следует применить формулы:
γ = α — β
tan γ = tan (α — β)
Решение очевидно:
Вопросы занятия:
· рассмотрим углы между пересекающимися и
скрещивающимися прямыми в пространстве.
Материал урока.
Напомню, что два луча
ОА и O1A1 в пространстве, не лежащие на одной прямой,
называются сонаправленными, если они параллельны и лежат в одной
полуплоскости с границей ОO1. Если
стороны двух углов соответственно сонаправленны, то такие углы равны.
Как вы уже знаете, любые
две пересекающиеся прямые лежат в одной плоскости и образуют четыре
неразвернутых угла. Если известен
один из этих углов, то можно найти и другие три угла.
Определение. Если пересекающиеся прямые образуют тупые и острые
углы, то углом между этими прямыми называется тот, который не
превосходит любой из трех остальных углов, т.е. наименьший из углов.
Если пересекающиеся
прямые образуют четыре равных угла, то угол между этими прямыми равен девяносто
градусов.
Пусть α – тот из углов,
который не превосходит любого из трех остальных углов. Тогда говорят, что угол
между пересекающимися прямыми равен α. Очевидно, что угол альфа между двумя пересекающимися
прямыми удовлетворяет условию: .
Теперь введем понятие угла
между скрещивающимися прямыми. Пусть нам даны две скрещивающиеся прямые а и
b. Возьмем произвольную точку М1 в
пространстве и проведем через нее прямые A1B1, параллельные прямым а и b
соответственно.
Тогда углом между
скрещивающимися прямыми а и b называется угол между построенными пересекающимися
прямыми A1B1. Т. е. если угол между прямыми A1B1 равен φ, то будем говорить, что угол между скрещивающимися
прямыми а и b равен φ.
Докажем, что угол
между скрещивающимися прямыми не зависит от выбора точки М1.
Возьмем любую другую
точку М2 и проведем через нее прямые a2 и b2,
параллельные прямым а и b соответственно. Пусть угол между прямыми a1 и b1 равен α1, а угол между прямыми a2 и b2 равен α2.
Если прямые a1, b1, a2, b2 лежат в
одной плоскости, то по свойству накрест лежащих углов при параллельных прямых
угол α1 равен
углу φ и равен углу α2.
Пусть теперь прямые a1 и b1,
пересекающиеся в точке М1, лежат в одной плоскости. А прямые a2 и b2,
пересекающиеся в точке М2 лежат в другой плоскости.
Так как прямая a1 параллельна прямой а и прямая a2 параллельна прямой а, то по признаку параллельности
прямых в пространстве прямые a1 и a2 также параллельны. Так как прямая b1 параллельна прямой b и прямая b2 параллельна прямой b, то по
признаку параллельности прямых в пространстве прямые b1 и b2 параллельны.
Отметим на прямых a1 и a2 точки A1 и A2 так, чтобы
отрезки М1А1 и М2А2 были равны. На
прямых b1 и b2 отметим точки B1 и B2 так,
чтобы отрезки M1B1и M2B2 были равны.
Угол A1M1B1 равен углу α1, угол A2M2B2 равен α2.
Тогда стороны угла A1M1B1 и угла A2M2B2 попарно сонаправлены. По теореме о равенстве углов с
сонаправленными сторонами получаем, что угол A1M1B1 равен углу A2M2B2. Т. е. имеем, что угол α1 равен углу α2.
Таким образом, величина
угла между скрещивающимися прямыми не зависит от выбора точки M1.
Замечание. Угол между параллельными прямыми в пространстве считается
равным 0º.
Рассмотрим пример. Пусть у нас есть треугольная пирамида DABC.
На ее ребре DB взята точка Т.
Тогда угол между
скрещивающимися прямыми BC и АТ равен углу между прямой АТ и прямой TF,
которая проходит через точку Т параллельно прямой BC в плоскости BDC.
Рассмотрим еще
пример. Пусть есть параллелепипед ABCDA1B1C1D1. И пусть точка О – точка пересечения диагоналей грани
A1B1C1D1, а точка F – точка пересечения диагоналей
грани AA1B1B.
Тогда угол между
скрещивающимися прямыми C1D и OF равен углу между прямыми OF и прямой OK,
проходящей через точку О и параллельной прямой C1D в плоскости C1DA1.
Задача. Дана правильная пирамида .
– средняя линия грани
. Найдите угол между
прямыми и
.
Решение.
Запишем ответ: 90º
Задача. Дан куб . Найдите угол между
прямыми и
.
Решение.
Ответ: 60º.
Подведем итоги
урока. На этом уроке мы рассмотрели
углы между пересекающимися и скрещивающимися прямыми. А также решили несколько
задач на нахождение скрещивающихся углов.
Угол между прямыми на плоскости
Определение. Если
заданы две прямые y = k1 x
+ b1 ,
y = k2x
+ b2 ,
то острый угол между этими прямыми будет
определяться как

Две
прямые параллельны, если k1 =
k2 .
Две прямые перпендикулярны, если k1 =
-1/ k2 .
Теорема. Прямые
Ах + Ву + С = 0 и А 1 х
+ В1 у
+ С1 =
0 параллельны, когда пропорциональны
коэффициенты А1 =
λА, В1 =
λВ. Если еще и С1 =
λС, то прямые совпадают. Координаты
точки пересечения двух прямых находятся
как решение системы уравнений этих
прямых.
Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
Определение. Прямая,
проходящая через точку М1 (х1 ,
у1 )
и перпендикулярная к прямой у = kx + b
представляется уравнением:
Расстояние от точки до прямой
Теорема. Если
задана точка М(х0 ,
у0 ),
то расстояние до прямой Ах + Ву + С =0
определяется как

Доказательство. Пусть
точка М 1(х 1,
у 1)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М1 :
(1)
Координаты
x1 и
у1 могут
быть найдены как решение системы
уравнений:
Второе
уравнение системы – это уравнение
прямой, проходящей через заданную точку
М 0 перпендикулярно
заданной прямой. Если преобразовать
первое уравнение системы к виду:
A(x –
x 0 )
+ B(y – y0 )
+ Ax0 +
By0 +
C = 0,
то,
решая, получим:
Подставляя
эти выражения в уравнение (1), находим:
Теорема
доказана.
Пример.
Определить угол между прямыми: y = -3 x +
7; y = 2 x + 1.
k 1 =
-3; k 2 =
2; tgφ = 
φ= p /4.
Пример.
Показать, что прямые 3х – 5у + 7 = 0 и 10х +
6у – 3 = 0 перпендикулярны.
Решение.
Находим: k 1 =
3/5, k2 =
-5/3, k 1* k 2 = -1, следовательно, прямые
перпендикулярны.
Пример.
Даны вершины треугольника А(0; 1), B (6; 5),
C (12; -1). Найти уравнение высоты, проведенной
из вершины С.
Решение.
Находим уравнение стороны АВ: 
4 x = 6 y – 6;
2 x –
3 y + 3 = 0;
Искомое
уравнение высоты имеет вид: Ax + By + C = 0
или y = kx + b . k = .
Тогда y = 
Т.к. высота проходит через точку С, то
ее координаты удовлетворяют данному
уравнению: 
b = 17. Итого: .
Ответ:
3 x + 2 y – 34 = 0.
-
Криві
та поверхні другого порядку. Канонічні
рівняння кривих другого порядку (еліпс,
коло, гіпербола, парабола). Їх властивості.
|
Кривые |
||||||||||||||||||||||||||||
|
Типові практичні
завдання.
-
Знайти
загальний розв’язок неоднорідної
системи лінійних рівнянь за методом
Гауса -
Обчислити
комплексні корені:
.
-
Знайти
ГМТ:
.
-
З’ясувати,
чи є вектор
лінійною комбінацією векторів
?
.
-
Знайти
ранг системи векторів,
базу та подати решту векторів у вигляді
лінійної комбінації векторів з цієї
бази
,
.
-
Обчислити
визначник:
.
-
Обчислити
значення многочлена
від
матриці.
-
Знайти
обернену матрицю до матриці
.
-
Знайти
загальний розв’язок неоднорідної
системи лінійних рівнянь та фундаментальну
систему розв’язків відповідної
однорідної СЛР.

-
Знайти
ранг матриці в залежності від значення
параметру
.

-
Знайти
найбільший спільний дільник многочленів
і
.
-
Визначити
кратність кореня
многочлена
.
-
Відділити
кратні корені многочлена -
Побудувати
многочлен найменшого степеня, який має
корінь (-1) кратності 2; корені 3, 2-i,I—
прості, якщо коефіцієнти цього многочлена
– дійсні, комплексні. -
Знайти
базиси суми та перетину підпросторів
та
.
-
Довести,
що многочлени
утворюють базис простору
,
якщо.
-
Довести,
що кожна з двох систем векторів утворює
базис, та побудувати матрицю переходу
від базису Е до Е´, де
Е:
,
,
;
Е´:,
,
.
-
Розглянемо
площину
.
—
Знайти відстань від
до площини ;
—
Скласти рівняння площини, що проходить
через А паралельно площині.
-
Відомі
координати вершин тетраедра
.
—
Обчислитиоб’ємтетраедра.
— Скласти загальне
рівняння однієї
грані та канонічне рівняння одного
ребра тетраедра.
— Обчислити площу
трикутника АВС.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #








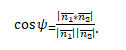
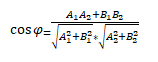
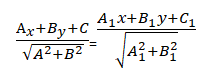
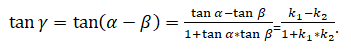

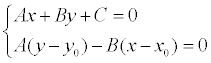






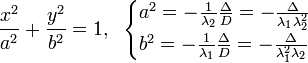








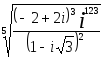 .
. .
. .
. .
. .
.