Как найти угол фигуры вписанной в окружность

Центральные и вписанные углы

О чем эта статья:

Центральный угол и вписанный угол

Окружность — замкнутая линия, все точки которой равноудалены от ее центра.

Определение центрального угла:

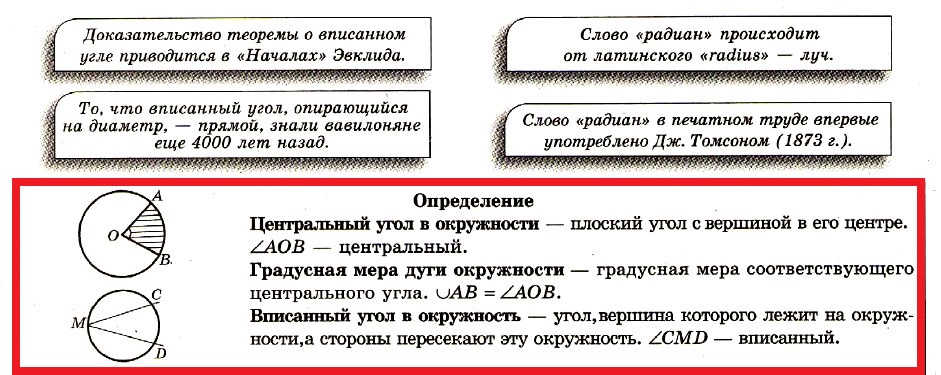
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.

На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF

Определение вписанного угла:

Вписанный угол — это угол, вершина которого лежит на окружности.

Вписанный угол равен половине дуги, на которую опирается.

На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC

Свойства центральных и вписанных углов

Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.

Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:

Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.

Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:

Вписанные углы окружности равны друг другу, если опираются на одну дугу:

ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.

Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:

ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.

Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:

На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.

Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Хорда — отрезок, соединяющий две точки на окружности.

Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.

AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.

Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.

ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.

Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.

ㄥBAC + ㄥBDC = 180°

Примеры решения задач

Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.

Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?

Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°

Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.

Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°

Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?

СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°

Углы, связанные с окружностью

Вписанные и центральные углы

Определение 1 . Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Определение 2 . Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.

Определение 3 . Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.

Теоремы о вписанных и центральных углах

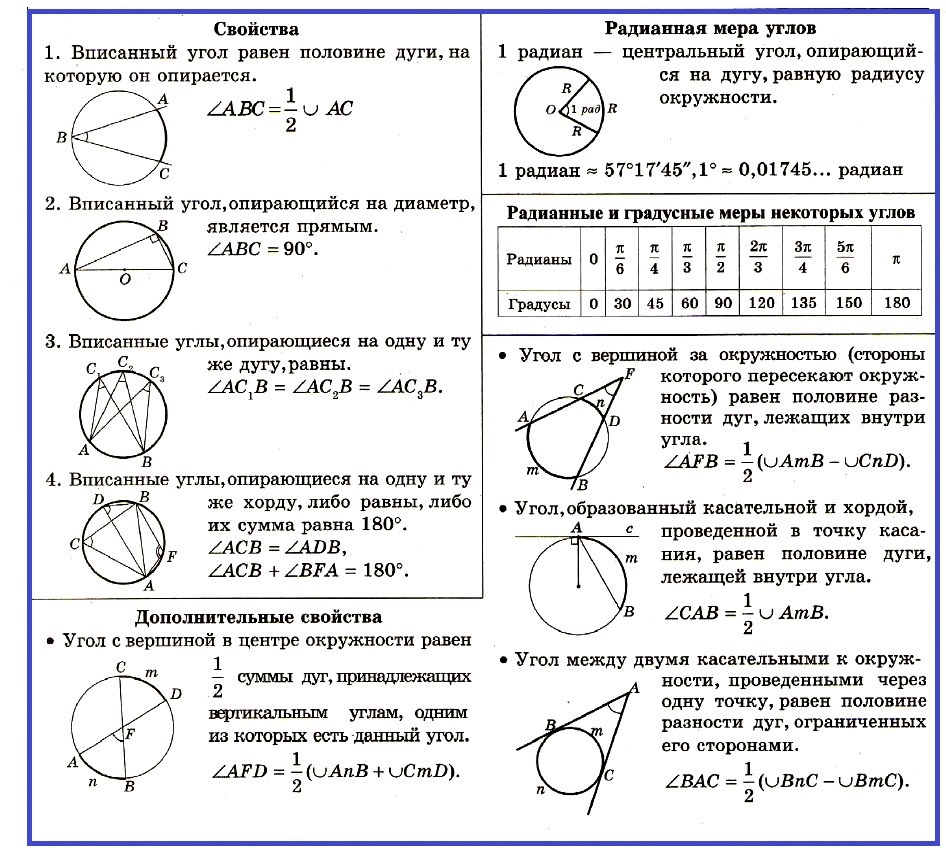
Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Середина гипотенузы прямоугольного треугольника является центром описанной
около этого треугольника окружности.

Фигура	Рисунок	Теорема
Вписанный угол
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же дугу равны.
Вписанный угол		Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
Вписанный угол		Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды
Вписанный угол		Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
Окружность, описанная около прямоугольного треугольника

Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Вписанные углы, опирающиеся на одну и ту же дугу равны.

Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды

Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180° , если их вершины лежат по разные стороны от этой хорды

Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр

Теоремы об углах, образованных хордами, касательными и секущими

Вписанный угол

Окружность, описанная около прямоугольного треугольника

Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами

Фигура	Рисунок	Теорема	Формула
Угол, образованный пересекающимися хордами
Угол, образованный секущими, которые пересекаются вне круга
Угол, образованный касательной и хордой, проходящей через точку касания
Угол, образованный касательной и секущей
Угол, образованный двумя касательными к окружности

Угол, образованный пересекающимися хордами хордами

Формула:

Угол, образованный секущими секущими , которые пересекаются вне круга

Формула:

Угол, образованный касательной и хордой хордой , проходящей через точку касания

Формула:

Угол, образованный касательной и секущей касательной и секущей

Формула:

Угол, образованный двумя касательными касательными к окружности

Формулы:

Доказательства теорем об углах, связанных с окружностью

Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.

Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).

Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.

Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

В этом случае справедливы равенства

и теорема 1 в этом случае доказана.

Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

В этом случае справедливы равенства

что и завершает доказательство теоремы 1.

Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 8.

Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 9.

Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства

что и требовалось доказать.

Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.

Доказательство . Рассмотрим рисунок 10.

Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства

что и требовалось доказать

Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.

Доказательство . Рассмотрим рисунок 11.

Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства

что и требовалось доказать.

Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.

Доказательство . Рассмотрим рисунок 12.

Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство

Центральный угол в окружности — плоский угол с вершиной в его центре.
Градусная мера дуги окружности — градусная мера соответствующего центрального угла.
Вписанный угол в окружность — угол, вершина которого лежит на окружности^ стороны пересекают эту окружность.

Доказательство теоремы о вписанном угле приводится в «Началах» Эвклида. То, что вписанный угол, опирающийся на диаметр, — прямой, знали вавилоняне еще 4000 лет назад.

Свойства вписанного угла. Радианная мера углов

Свойства вписанного угла:
1. Вписанный угoл равен половине дуги, на которую он опирается.
2. Вписанный угoл, опирающийся на диаметр, является прямым.
3. Вписaнные углы, опирающиеся на одну и ту же дугу, равны.
4. Вписaнные углы, опирающиеся на одну и ту же хорду, либо равны, либо их сумма равна 180°.

Радианная мера углов
1 радиан — центральный угол, опирающийся на дугу, равную радиусу окружности. 1 радиан = примерно 57°.
• Угол с вершиной за окружностью (стороны которого пересекают окружность) равен половине разности дуг, лежащих внутри угла.
• Угол,образованный касательной и хордой, с проведенной в точку касания, равен половине дуги, лежащей внутри угла.
• Угол между двумя касательными к окружности, проведенными через одну точку, равен половине разности дуг, ограниченных его сторонами.

Это конспект по теме «Центральный угол. Вписанный угол». Выберите дальнейшие действия:

источники:

http://www.resolventa.ru/spr/planimetry/cangle.htm

Центральный угол. Вписанный угол

Источник

План урока:

Центральный угол и градусная мера дуги

Вписанный угол

Углы между хордами и секущими

Теорема о произведении отрезков хорд

Задачи на квадратной решетке

Центральный угол и градусная мера дуги

Любые две точки на окружности разбивают ее на две дуги. Чтобы отличать эти дуги, на каждой из них ставят точку, которую и указывают в обозначении дуги:

Здесь красным цветом показана⋃АСВ, а синим – ⋃ADB. Однако иногда для простоты указывают только концы дуги, то есть используют обозначение ⋃AВ. Это делается тогда, когда ясно, о какой дуге окружности идет речь. Обычно всегда подразумевается та дуга, которая меньше.

Можно заметить, что дуги отличаются по размеру, поэтому возникает потребность их измерения. Для этого используют такое понятие, как градусная мера дуги.

Для ее определения необходимо соединить концы дуги с центром окруж-ти. В результате получаются радиусы, которые пересекаются в центре окружности. Угол между ними именуется центральным углом окруж-ти.

Для каждой дуги можно построить единственный центральный угол, поэтому логично измерять дугу с помощью такого угла. Правда, обратное неверно. На рисунке видно, что центральному углу ∠АОВ соответствует сразу две дуги: ⋃АСВ и ⋃АDB:

Поэтому условно считают, градусная мера той из двух дуг, которая меньше, как раз и равна центральному углу:

Дуги, также как отрезки или углы, можно складывать или вычитать. Например, пусть есть две дуги, ⋃AВ и ⋃ВС, чьи градусные меры составляют 40° и 30°.

Как найти ⋃АС? Ей соответствует центральный угол ∠АОС, который в свою очередь равен сумме ∠АОВ и ∠ВОС:

Диаметр делит окруж-ть на две равные друг другу дуги, которые называются полуокружностями. При этом диаметр окружности можно рассматривать как угол между двумя радиусами, равный 180°. Получается, что градусная мера полуокружности составляет 180°:

Вместе две полуокружности образуют полную окруж-ть. Получается, что градусная мера всей окруж-ти составляет 180° + 180° = 360°.

Этот факт известен и из жизни – когда кто-то делает полный оборот вокруг своей оси, говорят, что он повернулся на 360°. Теперь мы можем вернуться к случаю, когда две точки делят окруж-ть на две неравные друг другу дуги. Градусная мера меньшей из них будет равна величине соответствующего центрального угла (обозначим его как α). В сумме две дуги должны дать 360°. Значит, градусная мера большей дуги будет составлять 360° – α:

Задание. Точки А, В, С и D лежат на одной окруж-ти. Известно, что ⋃АСВ составляет 107°. Какова величина ⋃ADB?

Решение. Вместе дуги ⋃АСВ и ⋃АDВ образуют полную окруж-ть, поэтому их сумма равна 360°. Это позволяет составить уравнение и найти из него ⋃АDB:

Задание. Найдите величину ∠АОС на рисунке, если известны ⋃AВ и ⋃ВС:

Решение. Сначала найдем ⋃АС, учтя, что все три дуги, показанные на рисунке, в сумме составляют 360°:

Для доказательства построим две одинаковые хорды AВ и СD в окруж-ти и соединим их концы с центром:

В результате получились ∆АОВ и ∆ОСD. У них равны все три стороны, значит, сами эти треугольники равны. Тогда

∠COD = ∠AOB

Но эти углы – центральные для дуг ⋃AВ и ⋃CD. Получается, что у этих дуг одинаковы их градусные меры, поэтому они также равны, ч. т. д.

Примечание. Всякая хорда окружности разбивает ее на две дуги – большую и меньшую. В данном правиле говорится именно равенстве меньших дуг.

Задание. На окруж-ти отмечены точки А, В и С так, что хорды AВ, ВС и АС равны. Найдите угол между радиусами окружности АО и ВО.

Решение.

Дуги ⋃AВ, ⋃ВС и ⋃АС стянуты равными хордами AВ, ВС и АС. Значит, они одинаковы. Но в сумме эти три дуги образуют окруж-ть величиной в 360°. Значит, каждая из этих дуг втрое меньше:

⋃AВ = ⋃BC = ⋃AC = 360°:3 = 120°

∠АОВ – центральный для ⋃AВ, значит, он равен ее градусной мере, то есть он составляет 120°.

Ответ: 120°.

Вписанный угол

В окруж-ти можно построить ещё один угол, который именуют вписанным углом. Его отличие от центрального заключается в том, что его вершина лежит на окруж-ти, а не в ее центре. Сторонами же вписанного угла являются хорды окруж-ти.

Здесь дуга ⋃ВС находится внутри угла, а ее концы лежат на его сторонах. В таких случаях говорят, что ∠ВАС опирается на дугу ВС. Оказывается, что между величиной вписанного угла и дугой, на которую он опирается, есть взаимосвязь.

Обозначим вписанный угол ∠СAВ буквой α. Так как радиусы АО и ОС одинаковы, то ∆АОС – равнобедренный, и тогда углы при его основании будут одинаковы:

∠OCA = ∠OAC = α

∠СОВ – внешний для ∆АОС. Напомним, что такой угол равен сумме тех 2 углов треуг-ка, которые с ним не смежны. В частности, в данном случае можно записать

∠СОВ = ∠OCA = ∠OAC = α + α = 2α

Но этот же угол – центральный, и его величина равна ⋃ВС:

⋃BC = 2α

Получается, что дуга вдвое больше вписанного угла.

Далее рассмотрим случай, когда диаметр, проведенный из вершины вписанного угла, делит его на две части:

В этом случае вписанный угол ∠СAВ можно представить как сумму углов ∠САD (обозначен как α)и ∠ВАD (обозначен как β). Мы уже доказали, что дуги, на которые опираются эти углы, вдвое больше самих углов:

Осталось рассмотреть третий случай, при котором обе стороны вписанного угла ∠ВАС лежат по одну сторону от диаметра:

Если здесь обозначить ∠САD как α, а ∠ВАD как β, то интересующий нас ∠СAВ можно представить как их разность:

Итак, во всех трех возможных случаях вписанный угол оказывается вдвое меньше дуги, на которую он опирается.

Задание. Найдите ∠ВАС на рисунке:

Задание. Найдите вписанный ∠AВС, сели прилегающие к нему дуги ⋃AВ и ⋃ВС равны 100° и 128°.

Решение. В сумме дуги ⋃АС, ⋃ВС и ⋃AВ образуют окруж-ть, поэтому их сумма составляет 360°. Тогда можно найти ⋃АС:

Задание. Найдите дугу ⋃SM на рисунке:

Решение. Сначала найдем дугу ⋃MN, она вдвое больше соответствующего ей вписанного угла:

⋃NM = 2*∠NSM = 2*35° = 70°

Заметим, что ⋃SN– это полуокружность, то есть она составляет 180°. При этом ⋃SM и ⋃MN вместе как раз образуют эту полуокружность, то есть их сумма также составляет 180°. Значит, ⋃МS можно найти, вычтя из полуокружности ⋃MN:

⋃MS = ⋃SN — ⋃MN = 180° — 70° = 110°

Ответ: 110°.

Заметим, что для одной дуги можно построить несколько вписанных углов. Каждый из них будет равен половине дуги, то есть все эти углы окажутся одинаковыми.

Задание. Найдите ∠АСD на рисунке:

Решение. Так как ∠ACD и ∠ABD опираются на одну дугу ⋃AD, то они должны быть одинаковыми:

∠ACD = ∠ABD = 63°

Ответ: 63°.

Задание. Докажите, что две дуги, находящиеся между двумя параллельными секущими окруж-ти, равны друг другу.

Решение.

Нам надо доказать, что ⋃AВ и ⋃CD равны, если АС||BD. Проведем секущую ВС:

∠СВD и ∠АСВ равны, ведь они накрест лежащие. Получается, что ⋃AВ и ⋃CD являются основаниями равных вписанных углов. Отсюда вытекает, что эти дуги должны быть равными.

Напомним, что диаметр разбивает окруж-ть на две дуги по 180°. Отсюда можно сделать вывод – любой угол, опирающийся на полуокружность, должен составлять 180°:2 = 90°:

Задание. Диаметр окруж-ти AВ равен 17. Хорда ВС имеет длину 8. Какова длина хорды АС?

Решение.

Так как ∠АСВ опирается на диаметр AВ, то он прямой. Значит, и ∆АСВ – прямоугольный, причем диаметр AВ в нем – гипотенуза. Неизвестный катет можно найти по теореме Пифагора:

Задание. Окруж-ть разбита на две дуги, ⋃AВС и ⋃СDA. Известно, что ∠AВС = 72°. Найдите ∠ADC.

Решение.

Зная ∠AВС, мы легко найдем дугу ⋃ADC, она вдвое больше опирающегося на нее вписанного угла:

Углы между хордами и секущими

До этого мы рассматривали простые углы в окруж-ти, вершины которых лежали либо на самой окруж-ти, либо в ее центре. Однако иногда хорды и секущие пересекаются в другой точке, либо внутри, либо вне окруж-ти. Рассмотрим подобные задачи.

Более прост случай, когда необходимо найти угол между двумя пересекающимися хордами. Пусть хорды при пересечении образовали дуги ⋃AВ и ⋃СD величиной α и β. Каков угол между ними?

Проведем ещё одну хорду АD. В результате получим вписанные ∠САD и ∠ADB, которые будут равны половинам от соответствующих дуг, то есть α/2 и β/2. Интересующий нас ∠СPD оказывается внешним для ∆APD, и потому равен сумме двух углов в ∆APD (тех, которые с ним не смежны), то есть он составляет величину α/2 + β/2:

Величину α/2 + β/2 можно записать и иначе, вынеся множитель 1/2 за скобки:

α/2 + β/2 = (α + β)/2

Эту величину можно назвать полусуммой дуг, на которые опирается интересующий нас угол.

Задание. Найдите ∠МКВ на рисунке:

Решение. Интересующий нас угол опирается на хорды величиной 38° и 42°. Значит, он равен половине от их суммы:

∠MKB = (42° + 38°)/2 = 80°/2 = 40°

Ответ: 40°.

В более сложном случае необходимо найти угол между секущими, которые пересекаются вне окруж-ти. При этом известны дуги, образованные этими секущими:

Снова проведем хорду АD, чтобы у нас получились два вписанных угла, ∠ADB и ∠СAD, которые соответственно будут иметь величину β/2 и α/2:

Теперь уже ∠САD оказывается внешним для ∆ADK, а потому он является суммой двух других углов:

В итоге получили, что угол между секущими составляет половину от разности дуг, которые они отсекают от окруж-ти.

Задание. Найдите на рисунке величину∠К, если ⋃AВ и ⋃СD соответственно равны 42° и 130°:

Решение. В этой задаче просто используем доказанную теорему об углах между секущими. Искомый угол составляет половину от разности дуг, заключенных между секущими:

∠K = (130° — 42°):2 = 88°/2 = 44°

Ответ: 44°.

Теорема о произведении отрезков хорд

Можно заметить, что при пересечении двух хорд образуется пара подобных треугольников. Пусть хорды ADи ВС пересекаются в точке K. Добавим хорды AВ и СD и получим ∆AВК и ∆КСD:

На дугу ⋃BD опираются вписанные углы∠А и ∠С, значит, они одинаковы. Также на одну дугу АС опираются ∠D и∠В, поэтому и они одинаково. Равенство двух углов уже означает, что треугольники подобны по первому признаку подобия (дополнительно можно заметить, что ∠АКВ и ∠СКD равны как вертикальные углы).

Из подобия ∆AВК и ∆СКD вытекает пропорция между их сторонами:

Перемножив члены пропорции крест накрест, получим соотношение:

AK*KD = CK*BK

В результате нам удалось доказать следующее утверждение:

Задание. Хорды AВ и CD пересекаются в точке М. Известны, что АМ = 9, МВ = 3, МС = 2. Какова длина отрезка МD?

Решение.

Хорда AВ разбивается на отрезки АМ и МВ, а хорда CD – на отрезки СМ и МD. Произведения этих отрезков одинаковы:

AM*MB = CM*MD

Подставим в это равенство известные величины

Рассмотрим ещё одну геометрическую конструкцию. Пусть из некоторой точки А к окруж-ти проведена как касательная к окружности АК, так и секущая, пересекающая окруж-ть в точках В и С:

Какие здесь есть взаимосвязи между углами и длинами отрезков? Для начала проведем хорды ВК и СК, а также радиусы ОК и ОВ. Обозначим буквой α угол ∠ВСК. Он вписанный, поэтому дуга, на которую он опирается (это ⋃ВК), вдвое больше и равна 2α. Тогда и центральный угол ∠ВОК также составляет 2α:

Теперь исследуем ∆ВОК. Он равнобедренный (ВО и ОК – одинаковые радиусы), поэтому углы при его основании совпадают:

Итак, углы при основании ∆ОВК, в частности ∠ОКВ, равны 90° – α. Заметим, что ∠ОКА – прямой, так как образован радиусом ОК и касательной АК, при этом он состоит из двух углов, ∠АКВ и ∠ВКО. Это позволяет найти ∠АКВ:

В результате мы получили важный промежуточный результат – угол между касательной и хордой, проведенной из точки касания, вдвое меньше образующейся при этом дуги.

Вернемся к картинке с секущей. Изначально как α мы обозначили ∠ВСК, но в результате получили, что и ∠АКВ = α.

Рассмотрим ∆AВК и ∆САК. У них есть общий∠А, а также одинаковые ∠AКВ и ∠ВСК, которые отмечены буквой α. Значит, ∆AВК и ∆САК подобны, поэтому мы имеем право записать пропорцию между его сторонами:

Здесь отрезок АС можно назвать секущей, а AВ – ее внешней частью. Тогда выведенное отношение можно сформулировать так:

Решение. Сначала находим длину всей секущей, пользуясь доказанной теоремой:

Решение. Проведем из точки А ещё и касательную АК к окруж-ти:

Величину квадрата касательной АК можно найти, используя секущую АС. Сначала вычислим длину АС:

Ответ: 3,8.

Задачи на квадратной решетке

Рассмотрим несколько несложных задач, часто встречающихся на экзаменах.

Задание. Найдите ∠AВС на рисунке:

Решение. Здесь следует заметить, что расстояние между А и С составляет 8 клеток, при этом в окруж-ть как раз можно вписать квадрат со стороной 8.

Такой квадрат разобьет окруж-ть на 4 дуги, причем так как эти дуги опираются на хорды одинаковой длины, то они и сами равны. Вся окруж-ть составляет 360°, значит, каждая из этих дуг составляет 360°:4 = 90°. ∠AВС – вписанный, то есть он составляет половину дуги, на которую он опирается, а это⋃АС, равная 90°. Тогда

∠ABC = 90°:2 = 45°

Ответ: 45°.

Задание. Найдите ∠AВС, используя рисунок:

Решение. Используя рассуждения из предыдущей задачи, легко определить, что∠А составляет 45°.При этом ∆AВС – равнобедренный, и ВС – его основание. Это следует хотя бы из того факта, что высота АН делит сторону ВН пополам.

Углы∠В и ∠С одинаковы, так как лежат при основании равнобедренного треуг-ка. Найдем их, используя тот факт, что все 3 угла в ∆AВС составляют в сумме 180°:

Задание. Вычислите ∠AВС:

Решение. Снова в окруж-ть можно вписать квадрат со стороной 8 клеток. Из этого следует что ⋃АВС составляет 90° (показана фиолетовым цветом):

Но ∠АВС опирается на синюю дугу. Так как вместе фиолетовая и синяя дуга составляют окружность, равную 360°, то синяя дуга должна быть равна 360° – 90° = 270°. ∠АВС как вписанный будет вдвое меньше, то есть он равен 270°:2 = 135°.

Ответ: 135°.

Задание. Чему равен ∠AВС на рисунке?

Решение.

Если вписать в окруж-ть квадрат то он разобьет окруж-ти на дуги по 90°. В свою очередь точка А является серединой такой дуги, то есть она разбивает ее на две дуги по 45°.

∠AВС как вписанный будет вдвое меньше, то есть он равен 22,5°.

Источник

mat:geom:circle-angles

Содержание

Вписанный и центральный углы. Касательная

Угловой мерой дуги окружности является величина центрального угла, опирающегося на эту дугу.

Центральный угол — угол с вершиной в центре окружности.

Центральный угол равен градусной мере дуги, на которую опирается (по определению).

Если провести два радиуса, то образуется два центральных угла (сумма которых 360°) и две дуги окружности (сумма длин которых 2πR). Большему центральному углу соответствует большая дуга.

Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают эту окружность.

Когда говорят, что вписанный угол опирается на дугу — имеют в виду часть окружности, не содержащую вершину угла.

Проще говоря, угол (и центральный и вписанный) опирается на ту дугу, которая принадлежит части плоскости между сторонами угла.

Радианы — отношение длины s стягивающей дуги к её радиусу r. Таким образом, на единичной окружности величина центрального угла в радианах равна длине стягивающей дуги.

Любой конкретной дуге окружности можно сопоставить единственный центральный и бесконечное множество вписанных углов.

Теорема. Вписанный угол равен половине градусной меры дуги, на которую он опирается, или иначе говоря, равен половине центрального угла, опирающегося на ту же дугу.

Следствия:

Вписанные углы, опирающиеся на одну дугу, равны.
Вписанные углы, опирающиеся на диаметр, равны 90° (прямые).

Следствие из 2-го следствия:

Гипотенуза прямоугольного треугольника является диаметром описанной около него окружности.

Касательная

Касательная прямая к окружности в евклидовой геометрии на плоскости — прямая, которая имеет с окружностью ровно одну общую точку. Также можно определить касательную как предельное положение секущей, когда точки пересечения её с окружностью бесконечно сближаются.

англ Tangent line (танго — касаться)

Две секущие образуют угол, в который попадают две дуги окружности. В этом случае говорят, что секущие высекают эти дуги.

Построение касательной

Соединить данную точку P и центр окружности O. На отрезке OP нужно «восстановить» прямоугольный треугольник. Воспользуемся тем, что если вписанный угол опирается на диаметр окружности, то этот угол прямой.

Разделим отрезок OP пополам — получили точку H. Радиусом OH проводим еще одну окружность. Точка пересечения окружностей и есть точка касания.

Касательная к двум окружностям

Общая касательная к двум окружностям может быть внешней, если обе окружности расположены с одной стороны от нее, и внутренней, если окружности расположены с разных сторон касательной.

Построение общей внешней касательной к двум окружностям радиусами R и r

Из центра окружности большего радиуса – точки O1 описывают окружность радиусом R – r (рисунок 47, а). Находят середину отрезка O2O1 – точку O3 и из нее проводят вспомогательную окружность радиусом O3O2 или O3O1. Обе проведенные окружности пересекаются в точках A и В. Точки O1 и B соединяют прямой и в пересечении ее с окружностью радиусом R определяют точку касания D (рисунок 47, б). Из точки O2 параллельно прямой O1D проводят линию до пересечения с окружностью радиусом r и получают вторую точку касания C. Прямая CD является искомой касательной. Так же строится вторая общая внешняя касательная к этим окружностям (прямая EF).

напоминает яйцо — скорлупа и желток — это две окружности радиуса R и r, а белок — это кольцо толщиной R-r

Построение общей внутренней касательной к двум окружностями радиусов R и r

Из центра любой окружности, например: точки O1, описывают окружность радиусом R + r (рисунок 48, а). Разделив отрезок O2O1 пополам, получают точку O3. Из точки O3 как из центра описывают вторую вспомогательную окружность радиусом O3O2 = O3О1 и отмечают точки A и В пересечения вспомогательных окружностей. Соединив прямой точки A и O1 (рисунок 48, б), в пересечении ее с окружностью радиуса R получают точку касания D. Через центр окружности радиуса r проводят прямую, параллельную прямой O1D, и в пересечении ее с заданной окружностью определяют вторую точку касания С. Прямая CD – внутренняя касательная к заданным окружностям. Аналогично строится и вторая касательная EF.

Общие касательные к двум окружностям — варианты касательных к двум окружностям, сохранено в pdf

также хорошо написано в Tangent lines to circles — Wikipedia

Касательные прямые и бильярд

Система касательных прямых прицеливания битка использует прямую, проходящую через середину кия, для создания двух касательных прямых от битка в направлении прицельного шара. Две касательные прямые и прямая через середину битка пересекают прямую, проходящую через середину прицельного шара и центр лузы. Необходимо направить удар так, чтобы конечное положение битка (воображаемый шар на рисунке) касалось прицельного шара в точке касания прямой, перпендикулярной направлению на лузу (на рисунке эта касательная выделена зелёным цветом).

Угол между касательной и хордой

Угол между касательной и хордой, проведенной через точку касания, равен половине угловой величины дуги, заключенной между ними.

Угол между касательной и хордой является вырожденным случаем вписанного угла, в котором вершина угла совпадает с одним из концов дуги.

Доказательство

Касательная перпендикулярна радиусу, проведенному в точку касания.

Пусть $angle MCA=varphi$. Тогда $angle OCA = 90 ^{circ}-varphi$. Треугольник $OCA$ – равнобедренный, $OA = OC$ (как радиусы окружности). Значит, $angle AOC= 180 ^{circ}-2left ( 90 ^{circ} — varphi right )=2varphi$, что и требовалось доказать.

Заметим, что $angle ABC = varphi$ – как вписанный, опирающийся на ту же дугу.

Теорема о секущей и касательной

Квадрат отрезка касательной равен произведению длин отрезков секущей.

или

Квадрат касательной равен произведению секущей на ее внешнюю часть.

$ PM cdot PN=PT^2$

Мысленно сближать точки пересечения секущей с окружностью: тогда PN будет стремиться к PT с одной стороны, а PM — с другой стороны, а произведение их длин будет стремиться к $PT^2$

Доказательство следует из подобия треугольников PMT и PTN https://i.imgur.com/C5EMn1t.jpg

Угол между секущими

Если точка пересечения двух секущих к окружности находится внутри окружности, то угол между секущими равен полусумме дуг, которые они высекают.

Если точка пересечения двух секущих к окружности находится вне окружности, то угол между секущими равен половине разности дуг, которые они высекают.

Теорема выполняется, если заменить секущую на касательную к окружности.

Свойства дуг, хорд и углов окружности

Если хорды равноудалены от центра окружности, то они равны.
Если хорды равны, то они равноудалены от центра окружности.
Большая из двух хорд находится ближе к центру окружности.
Наибольшая хорда является диаметром.
Если диаметр делит хорду пополам, то он перпендикулярен ей.
Если диаметр перпендикулярен хорде, то он делит ее пополам.
Равные дуги стягиваются равными хордами.
Дуги, заключенные между параллельными хордами, равны.
Все вписанные углы, опирающиеся на одну и ту же дугу, раны.
Все вписанные углы, опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
Все вписанные углы, опирающиеся на диаметр, прямые.
Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр.
Любая пара углов, опирающихся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180.
Другими словами: Вписанные углы, опирающиеся на одну и ту же хорду, либо равны, либо их сумма 180°.
Угол между хордой и касательной измеряется половиной содержащейся в этом угле дуги окружности.

Угол с вершиной внутри окружности: Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами.

Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.

Доказательство. Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство α = π – γ. Далее получаем γ = 2π — β, значит, α = β — π. Складываем два выражения для α и делим пополам. α = (β-γ)/2

Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла. α = (β-γ)/2

Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.

Еще рисунки:

∠ABC = ½∪AB Кут між хордою і дотичною

∠AEB = ½(∪AB+∪CD) Кут між хордами

∠AED = ½(∪AB-∪CD) Кут між січними

mat/geom/circle-angles.txt

· Последние изменения: 2020/02/06 00:36 —

Источник

Вписанный угол

Содержание:

Что такое вписанный угол
Формулировка теоремы о вписанном угле, ее следствия
Чему равен вписанный угол в окружности

Что такое вписанный угол

Определение

Вписанный угол — угол, у которого вершина расположена на окружности, а стороны имеют точки пересечения с этой окружностью.

Вписанный угол опирается на дугу, образованную им на окружности, или опирается на хорду, которая соединяет концы этой дуги.

Свойства вписанного угла:

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

любые вписанные углы, которые опираются на одну и ту же дугу, равны;
любые вписанные углы, которые опираются на одну и ту же хорду, с вершинами, расположенными по одну сторону от этой хорды, равны;
все вписанные углы, которые опираются на диаметр окружности, являются прямыми;
каждая пара углов, которые опираются на одну и ту же хорду, с вершинами, расположенными по разные стороны хорды, составляют в сумме (180^{0}.)

Согласно перечисленным правилам, можно значительно упростить измерение углов, вписанных в окружность. Например, пусть в окружность вписан четырехугольник ABCD с (angle A={{105}^{circ}}), (quad angle B={{64}^{circ}}). Углы A и C опираются на одну хорду BD, но лежат по разные стороны от нее, и их сумма составляет (180^{0}). Таким образом:

(angle C={{180}^{circ}}-angle A={{180}^{circ}}-{{105}^{circ}}={{75}^{circ}})

(angle D={{180}^{circ}}-angle B={{180}^{circ}}-{{64}^{circ}}={{116}^{circ}})

Следовательно, ( angle C={{75}^{circ}}, quad angle D={{116}^{circ}})

Можно рассмотреть пару треугольников ABC и ABD. Предположим, что Угол C равен ({{50}^{circ}}), сторона BD проходит через центр окружности. Также Треугольники ABC и ABD имеют общую сторону AB, на которую опираются углы C и D. Таким образом:

(angle C=angle D={{50}^{circ}})

Треугольник ABD обладает углом A, который является прямым. Это объясняется тем, что данный угол опирается на диаметр BD. Исходя из этого, можно найти угол В:

(angle B={{180}^{circ}}-angle A-angle D={{180}^{circ}}-{{90}^{circ}}-{{50}^{circ}}={{40}^{circ}})

В результате (angle B={{40}^{circ}})

Можно выделить несколько важных закономерностей, справедливых в случае вписанных углов, которые пригодятся при решении задач по геометрии:

вписанный угол равен 1/2 центрального угла, который опирается на ту же дугу: (beta =frac{alpha }{2};)
длина хорды составляет: (l =2r*sin frac{alpha }{2}=2r*sin beta;)
длина дуги равна: (l =alpha *r), угол (alpha) в радианах;
длину окружности можно вычислить по формуле: (L=2pi *r;)
площадь круга определяется, как: (S=pi r^{2}.)

Вписанный угол

Формулировка теоремы о вписанном угле, ее следствия

Определение

Теорема о вписанном угле: вписанный угол равен половине дуги, на которую он опирается.

Исходя из определения, вписанный угол содержит такое количество угловых радиусов, минут и секунд, сколько включает половина дуги, которая служит его опорой. Для доказательства теоремы необходимо рассмотреть три разных случая расположения вписанного угла.

В первом случае центр окружности O находится на стороне вписанного угла ABС.

Теорема о вписанном угле

Если построить радиус AO, то получится треугольник АBO. В данной геометрической фигуре радиусы в виде отрезков OA и OB будут равны. Таким образом, угол ABO равен углу BAO. Относительно рассматриваемого треугольника, угол AOС является внешним. В связи с этим, данный угол соответствует сумме углов ABO и BAO, а также равен двойному углу ABO. Можно сделать вывод, что угол ABO является половиной центрального угла AOС. С другой стороны, этот угол измеряется дугой AC. Таким образом, вписанный угол ABС равен половине дуги AC.

Во втором случае центр окружности O расположен между сторонами вписанного угла ABС.

Теорема о вписанном угле

С помощью построения диаметра BD угол ABС будет поделен на два угла. Один из рассматриваемых углов, согласно доказательству теоремы в первом случае, равен половине дуги AD. Второй угол соответствует половине дуги СD. Таким образом, угол ABС определен, как (AD+DС) /2, то есть 1/2 AC.

В третьем случае центр окружности O не принадлежит вписанному углу ABС.

Теорема о вписанном угле

Построив диаметр BD, получим, что угол ABС равен равности углов ABD и CBD. Однако, углы ABD и CBD измеряются, согласно доказанной ранее теореме, половинами дуг AD и СD. Исходя из того, что угол ABС соответствует половине разности (AD-СD), он равен половине дуги АС.

Теорема о вписанном в окружность угле обладает несколькими следствиями.

Следствие 1

Какие-либо из вписанных в окружность углов, которые опираются на одну и ту же дугу, являются одинаковыми, то есть равны между собой, так как любой из них равен половине одной и той же дуги.

Следствие 2

Вписанный в окружность угол, который опирается на ее диаметр, является прямым, так как любой подобный угол равен половине полуокружности, значит, соответствует .

Теорема о вписанном угле

Чему равен вписанный угол в окружности

Вписанный в круг угол состоит из двух хорд и вершины, которая расположена на окружности. К примеру, треугольник АВС имеет вписанный угол АРВ, который образован парой лучей и вершиной, принадлежащей окружности:

Чему равен вписанный угол в окружности

Величина вписанного угла соответствует ½ его дуги, то есть составляет ½ дуги АВ: APB=84/2 = 42.

В том случае, когда пара углов опирается на одну и ту же дугу, они будут равны друг другу. Например, угол BAC равен углу BDC, исходя из того, что данные углы опираются на одну и ту же дугу:

Чему равен вписанный угол в окружности

(∠ CAB = frac{1}{2} ∠BOC)

(∠ CDB =frac{1}{2} ∠ BOC)

При известной длине малой дуги и радиусе, вписанный угол можно вычислить по формуле:

(X= frac{90*Lpi }{R})

Предположим, что в окружности построили хорду AB. По разные стороны от нее отметили точки C и D, и соединили их с концами хорды. Полученный угол ACB больше, чем угол ADB в два раза. Так как углы ACB и ADB опираются на одну хорду и расположены по разные стороны от нее, то в сумме рассматриваемые углы составляют 180 градусов. Если принять (angle ADB) за x, то (angle ACB) составит 2x, а их сумма равна:

x+2x=180

При решении данного уравнения, x=60. Таким образом:

(angle ADB={{60}^{circ}}, text{a} angle ACB={{120}^{circ}})

В результате, (angle ADB={{60}^{circ}}, angle ACB={{120}^{circ}})

Источник