Как найти угол касательной к оси ординат

Геометрический смысл производной

Если плохо разбираешься в производной, то вот тебе полноценный гид по ней, с текстом, примерами и вебинарами: «Производная функции – геометрический смысл и правила дифференцирования»!

Рассмотрим график какой-то функции ( y=fleft( x right)):

Выберем на линии графика некую точку ( A). Пусть ее абсцисса ( {{x}_{0}}), тогда ордината равна ( fleft( {{x}_{0}} right)).

Затем выберем близкую к точке ( A) точку ( B) с абсциссой ( {{x}_{0}}+Delta x); ее ордината – это ( fleft( {{x}_{0}}+Delta x right)):

Проведем прямую через эти точки. Она называется секущей (прямо как в геометрии).

Обозначим угол наклона прямой к оси ( Ox) как ( alpha ).

Как и в тригонометрии, этот угол отсчитывается от положительного направления оси абсцисс против часовой стрелки.

Какие значения может принимать угол ( alpha )?

Как ни наклоняй эту прямую, все равно одна половина будет торчать вверх. Поэтому максимально возможный угол – ( 180{}^circ ), а минимально возможный – ( 0{}^circ ).

Значит, ( alpha in left[ 0{}^circ ;180{}^circ right)). Угол ( 180{}^circ ) не включается, поскольку положение прямой в этом случае в точности совпадает с ( 0{}^circ ), а логичнее выбирать меньший угол.

Возьмем на рисунке такую точку ( C), чтобы прямая ( AC) была параллельна оси абсцисс, а ( BC) – ординат:

По рисунку видно, что ( AC=Delta x), а ( BC=Delta f).

Тогда отношение приращений:

Давай теперь уменьшать ( Delta x).

Тогда точка ( B) будет приближаться к точке ( A). Когда ( Delta x) станет бесконечно малым ( left( Delta xto 0 right)), отношение ( frac{Delta f}{Delta x}) станет равно производной функции в точке ( {{x}_{0}}).

Что же при этом станет с секущей?

Точка ( B) будет бесконечно близка к точке ( A), так что их можно будет считать одной и той же точкой.

Но прямая, имеющая с кривой только одну общую точку – это ни что иное, как касательная (в данном случае это условие выполняется только на небольшом участке – вблизи точки ( A), но этого достаточно).

Говорят, что при этом секущая занимает предельное положение.

Угол наклона секущей к оси ( displaystyle Ox) назовем ( varphi ). Тогда получится, что производная

( {f}’left( {{x}_{0}} right)underset{Delta xto 0}{mathop{=}},frac{Delta f}{Delta x}= {tg}varphi ),

то есть

Производная равна тангенсу угла наклона касательной к графику функции в данной точке

Поскольку касательная – это прямая, давай теперь вспомним уравнение прямой:

( y=kx+b).

За что отвечает коэффициент ( displaystyle k)? За наклон прямой. Он так и называется: угловой коэффициент.

Что это значит? А то, что равен он тангенсу угла между прямой и осью ( displaystyle Ox)!

То есть вот что получается:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k).

Но мы получили это правило, рассматривая возрастающую функцию. А что изменится, если функция будет убывающей?

Посмотрим: Теперь углы ( alpha ) и ( displaystyle varphi ) тупые. А приращение функции ( Delta f) – отрицательное.

Снова рассмотрим ( triangle ABC): ( angle B=180{}^circ -alpha text{ }Rightarrow text{ } {tg}angle B=- {tg}alpha ).

С другой стороны, ( {tg}angle B=frac{AC}{BC}=frac{-Delta f}{Delta x}).

Получаем: ( frac{-Delta f}{Delta x}=- {tg}alpha text{ }Rightarrow text{ }frac{Delta f}{Delta x}= {tg}alpha ), то есть все, как и в прошлый раз.

Снова устремим точку ( displaystyle B) к точке ( displaystyle A), и секущая ( displaystyle AB) примет предельное положение, то есть превратится в касательную к графику функции в точке ( displaystyle A).

Итак, сформулируем окончательно полученное правило:

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или (что то же самое) угловому коэффициенту этой касательной:

( {f}’left( {{x}_{0}} right)= {tg}varphi =k)

Это и есть геометрический смысл производной.

Окей, все это интересно, но зачем оно нам? Вот пример:

На рисунке изображен график функции ( displaystyle y=mathsf{f}left( x right)) и касательная к нему в точке с абсциссой ( {{x}_{0}}).

Найдите значение производной функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}).

Решение.

На рисунке у нас отмечено две точки, лежащие на касательной, координаты которых нам известны. Так давай достроим прямоугольный треугольник, проходящий через эти точки, и найдем тангенс угла наклона касательной!

Таким образом, производная функции ( displaystyle mathsf{f}left( x right)) в точке ( {{x}_{0}}) равна ( displaystyle 1,2).

Ответ: ( displaystyle 1,2).

Теперь попробуй сам.

Уравнение касательной к графику функций

А сейчас сосредоточимся на произвольных касательных.

Предположим, у нас есть какая-то функция, например, ( fleft( x right)=left( {{x}^{2}}+2 right)). Мы нарисовали ее график и хотим провести касательную к нему в какой-нибудь точке ( {{x}_{0}}). Например, в точке ( {{x}_{0}}=2).

Берем линейку, пристраиваем ее к графику и чертим:

Что мы знаем об этой прямой? Что самое важное нужно знать о прямой на координатной плоскости?

Поскольку прямая – это изображение линейной функции, очень удобно было бы знать ее уравнение. То есть коэффициенты ( k) и ( b) в уравнении

( y=kx+b).

Но ведь ( k) мы уже знаем! Это угловой коэффициент касательной, который равен производной функции в этой точке:

( k={f}’left( {{x}_{0}} right)).

В нашем примере будет так:

( {f}’left( x right)={{left( {{x}^{2}}+2 right)}^{prime }}=2x;)

Графически ( b) – это координата пересечения прямой с осью ординат (ведь ( displaystyle x=0) во всех точках оси ( displaystyle Oy)):

Проведём ( BCparallel Ox) (так, что ( triangle ABC) – прямоугольный).

Тогда ( angle ABC=alpha )(тому самому углу между касательной и осью абсцисс). Чему равны ( displaystyle AC) и ( displaystyle BC)?

По рисунку явно видно, что ( BC={{x}_{0}}), а ( AC=fleft( {{x}_{0}} right)-b). Тогда получаем:

( {f}’left( {{x}_{0}} right)= {tg}alpha =frac{AC}{BC}=frac{fleft( {{x}_{0}} right)-b}{{{x}_{0}}}text{ }Rightarrow text{ }b=fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right)).

Соединяем все полученные формулы в уравнение прямой:

( y=kx+b={f}’left( {{x}_{0}} right)cdot x+fleft( {{x}_{0}} right)-{{x}_{0}}cdot {f}’left( {{x}_{0}} right);)

Пример:

Найди уравнение касательной к графику функции ( fleft( x right)={{x}^{2}}-2x+3) в точке ( {{x}_{0}}=3).

Решение:

На этом примере выработаем простой…

Бонус: Вебинар из нашего курса по подготовке к ЕГЭ по математике

ЕГЭ №7. Производная функции — геометрический смысл, дифференцирование

На этом видео мы вспомним, что такое функция и её график, научимся искать производную некоторых функций, например, такой: y = 2×3 – 3×2 + x + 5. 

Мы разберём от А до Я все 7 типов задач, которые могут попасться в задаче №7 из ЕГЭ. Узнаем, на какие 3 фразы в условии задачи нужно обратить особое внимание, чтобы с лёгкостью решить задачу и не потерять баллы на ровном месте.  

Разберём все возможные ошибки, которые можно допустить в этих задачах. Мы поймём, что многие из этих задач решаются обычным подсчётом клеточек на графике! Главное – не перепутать, что нужно считать.

P.S. Не забудьте потом посмотреть родственную тему: «Интегралы на ЕГЭ. Первообразные элементарных функций».

Как найти тангенс угла наклона касательной

Геометрический смысл производной первого порядка функции F(х) представляет собой касательную прямую к ее графику, проходящую через заданную точку кривой и совпадающую с ней в этой точке. Причем значение производной в данной точке х0 является угловым коэффициентом или иначе – тангенсом угла наклона касательной прямой k = tg a = F`(х0). Вычисление данного коэффициента – одна из наиболее распространенных задач теории функций.

Инструкция

Запишите заданную функцию F(x), например F(x) = (x³ + 15х +26). Если в задаче явно указана точка, через которую проводится касательная, например, ее координата х0 = -2, можно обойтись без построения графика функции и дополнительных прямых на декартовой системе ОХY. Найдите производную первого порядка от заданной функции F`(x). В рассматриваемом примере F`(x) = (3x² + 15). Подставьте заданное значение аргумента х0 в производную функции и вычислите ее значение: F`(-2) = (3(-2)² + 15) = 27. Таким образом, вы нашли tg a = 27.

При рассмотрении задачи, где требуется определить тангенс угла наклона касательной к графику функции в точке пересечения этого графика с осью абсцисс, вам понадобится сначала найти числовое значение координат точки пересечения функции с ОХ. Для наглядности лучше всего выполнить построение графика функции на двухмерной плоскости ОХY.

Задайте координатный ряд для абсцисс, например, от -5 до 5 с шагом 1. Подставляя в функцию значения х, вычислите соответствующие им ординаты у и отложите на координатной плоскости полученные точки (х, у). Соедините точки плавной линией. Вы увидите на выполненном графике место пересечения функцией оси абсцисс. Ордината функции в данной точке равна нулю. Найдите численное значение соответствующего ей аргумента. Для этого заданную функцию, например F(x) = (4x² — 16), приравняйте к нулю. Решите полученное уравнение с одной переменной и вычислите х: 4x² — 16 = 0, x² = 4, х = 2. Таким образом, согласно условию задачи, тангенс угла наклона касательной к графику функции необходимо найти в точке с координатой х0 = 2.

Аналогично описанному ранее способу определите производную функции: F`(x) = 8*x. Затем вычислите ее значение в точке с х0 = 2, что соответствует точке пересечения исходной функции с ОХ. Подставьте полученное значение в производную функции и вычислите тангенс угла наклона касательной: tg a = F`(2) = 16.

При нахождении углового коэффициента в точке пересечения графика функции с осью ординат (ОY) выполните аналогичные действия. Только координату искомой точки х0 сразу следует принять равной нулю.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

Решение задач по математике онлайн

//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘

Калькулятор онлайн.
Уравнение прямой касательной к графику функции в заданной точке

Эта математическая программа находит уравнение касательной к графику функции ( f(x) ) в заданной пользователем точке ( x_0 ).

Программа не только выводит уравнение касательной, но и отображает процесс решения задачи.

Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Статью из энциклопедии о касательной прямой вы можете посмотреть здесь (статья из Википедии).

Если вам нужно найти производную функции, то для этого у нас есть задача Найти производную.

Обязательно ознакомьтесь с правилами ввода функций. Это сэкономит ваше время и нервы.
Правила ввода функций >> Почему решение на английском языке? >> Введите выражение функции ( f(x)) и число (x_0) — абсциссу точки в которой нужно построить касательную Найти уравнение касательной

Немного теории.

Угловой коэффициент прямой

Напомним, что графиком линейной функции ( y=kx+b) является прямая. Число (k=tg alpha ) называют угловым коэффициентом прямой, а угол ( alpha ) — углом между этой прямой и осью Ox

Уравнение касательной к графику функции

Если точка М(а; f(a)) принадлежит графику функции у = f(x) и если в этой точке к графику функции можно провести касательную, не перпендикулярную оси абсцисс, то из геометрического смысла производной следует, что угловой коэффициент касательной равен f'(a). Далее мы выработаем алгоритм составления уравнения касательной к графику любой функции.

Пусть даны функция у = f(x) и точка М(а; f(a)) на графике этой функции; пусть известно, что существует f'(a). Составим уравнение касательной к графику заданной функции в заданной точке. Это уравнение, как уравнение любой прямой, не параллельной оси ординат, имеет вид y = kx + b, поэтому задача состоит в нахождении значений коэффициентов k и b.

С угловым коэффициентом k все понятно: известно, что k = f'(a). Для вычисления значения b воспользуемся тем, что искомая прямая проходит через точку М(а; f(a)). Это значит, что если подставить координаты точки М в уравнение прямой, получим верное равенство: (f(a)=ka+b ), т.е. ( b = f(a) — ka ).

Осталось подставить найденные значения коэффициентов k и b в уравнение прямой:

Нами получено уравнение касательной к графику функции ( y = f(x) ) в точке ( x=a ).

Алгоритм нахождения уравнения касательной к графику функции ( y=f(x) )
1. Обозначить абсциссу точки касания буквой ( a )
2. Вычислить ( f(a) )
3. Найти (f'(x) ) и вычислить (f'(a) )
4. Подставить найденные числа ( a, f(a), f'(a) ) в формулу ( y=f(a)+ f'(a)(x-a) )

Касательная и нормаль к графику функции

Основные формулы

Пусть на некотором интервале X задана функция . Нас интересуют геометрические характеристики графика этой функции в некоторой заданной точке при значении аргумента , где . Пусть функция имеет в производную, которую будем обозначать как . Тогда через точку мы можем провести касательную к графику. Тангенс угла α между осью абсцисс x и касательной равен производной функции в точке :
(1) .
А само уравнение касательной имеет вид:
(2) .
В аналитической геометрии тангенс угла между прямой и осью абсцисс называют угловым коэффициентом прямой. Таким образом производная равна угловому коэффициенту касательной в .
См. Геометрический смысл производной

Прямая, перпендикулярная касательной, проведенной через точку , называется нормалью к графику функции в этой точке. Уравнение нормали имеет вид:
(3) .
См. Уравнение прямой с угловым коэффициентом ⇓

Пусть две кривые и пересекаются в точке . Тогда угол φ между касательными к этим кривым в точке называется углом между кривыми. Он определяется по формуле:
(4) , где .
Отсюда .
при .
Вывод формулы ⇓

Определения

Здесь мы приводим определения, которые встречаются в литературе, и имеют отношение к касательной и нормали. Вывод формул приводится в примере 1 ⇓.

Определение касательной приводится здесь. Уравнение касательной:
.

Касательная TM₀, нормаль M₀N, подкасательная TP, поднормаль PN. Нормалью к графику функции в точке называется прямая, перпендикулярная касательной, проведенной через эту точку. Уравнение нормали:
.
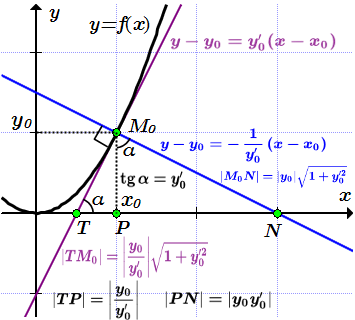
Отрезком касательной называют отрезок между точкой пересечения касательной с осью абсцисс и точкой .
.
Отрезком нормали называют отрезок между точкой пересечения нормали с осью абсцисс и точкой .
.
Подкасательной называют отрезок между точкой пересечения касательной с осью абсцисс и проекции точки на эту ось.
.
Поднормалью называют отрезок между точкой пересечения нормали с осью абсцисс и проекции точки на эту ось.
.
Углом между кривыми в точке их пересечения называют угол между касательными к кривым, проведенных через точку .

Полезные формулы из аналитической геометрии

Далее приводятся некоторые сведения из аналитической геометрии, которые могут оказаться полезными при решении задач.

Уравнение прямой, проходящей через две заданные точки и :
.
Здесь – направляющий вектор прямой.

Умножив это уравнение на , получим уравнение прямой в другом виде:
.
Здесь – вектор нормали прямой. Тогда само уравнение означает равенство нулю скалярного произведения векторов и .

Уравнение прямой, проходящей через точку параллельно вектору имеет вид:
.
Вектор называется направляющим вектором данной прямой. Это уравнение можно написать в параметрическом виде, введя параметр t :

Уравнение прямой, проходящей через точку перпендикулярно вектору имеет вид:
.
Вектор называется вектором нормали данной прямой.

Уравнение прямой с угловым коэффициентом k , проходящей через точку :
.
Угол α между прямой и осью x определяется по формуле:
.
Если две прямые взаимно перпендикулярны, то их угловые коэффициенты и связаны соотношением:
.

Уравнение прямой в отрезках, пересекающей оси координат в точках :
.

Примеры решения задач

Все примеры Ниже рассмотрены примеры решений следующих задач.
1. Найти уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали. Решение ⇓
2. Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде
, проведенных в точке . Решение ⇓
3. Заданной в неявном виде . Решение ⇓
4. Найти угол между кривыми и Решение ⇓

Пример 1

Составить уравнения касательной и нормали к кривой в точке . Найти длины отрезков касательной, нормали, подкасательной и поднормали.

Находим значение функции при :
.

Находим производную:
.
Находим производную в точке :
;
.

Находим уравнение касательной по формуле (2):
;
;
;
– уравнение касательной.
Строим касательную на графике. Поскольку касательная – это прямая, то нам нужно знать положения двух ее точек, и провести через них прямую.
При ;
при .
Проводим касательную через точки и .

Касательная и нормаль к графику функции y=x 2 в точке M₀(1;1).

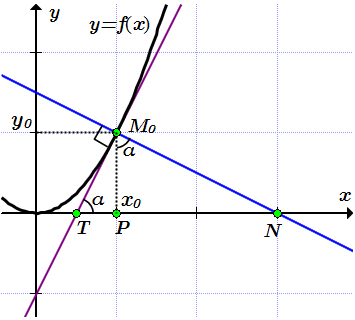
Найдем угол α между касательной и осью абсцисс по формуле (1):
.
Подставляем :
;
.

Находим уравнение нормали по формуле (3):
;
;
;
;
;
– уравнение нормали.
Строим нормаль по двум точкам.
При ;
при .
Проводим нормаль через точки и .

Находим длину отрезка касательной . Из прямоугольника имеем:
.
Поясним использованную формулу. Поскольку , то . Тогда
.
Подставляем :
.

Находим длину отрезка подкасательной . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка нормали . Поскольку и , то треугольники и подобны. Тогда . Из прямоугольника имеем:
.
Подставляем :
.

Находим длину отрезка поднормали . Из прямоугольника имеем:
.

Примечание.
При выводе формул, можно сначала определить длины отрезков подкасательной и поднормали, а затем из прямоугольников, по теореме Пифагора, найти длины отрезков касательной и нормали:
;
.

Уравнение касательной: ; уравнение нормали: ;
длина отрезка касательной: ; длина отрезка нормали: ; длина подкасательной: ; длина поднормали: .

Пример 2

Составить уравнения касательной и нормали к циссоиде, заданной в параметрическом виде , проведенных в точке .

Находим значения переменных при .
;
.
Обозначим эту точку как .

Находим производные переменных x и y по параметру t .
;
;
;
;
.

Подставляя , находим производную y по x в точке .
.

Касательная и нормаль к циссоиде в точке (2;2).

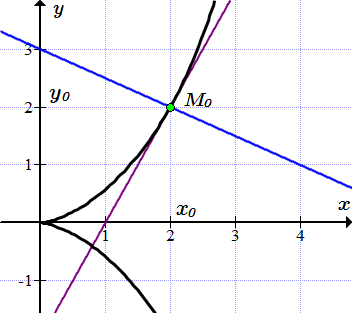
Применяя формулу (2), находим уравнение касательной к циссоиде, проходящей через точку .
;
;
;
.

Применяя формулу (3), находим уравнение нормали к циссоиде в точке .
;
;
;
.

Уравнение касательной: .
Уравнение нормали: .

Пример 3

Составить уравнения касательной и нормали к циссоиде, заданной в неявном виде:
(П3) ,
проведенных в точке .

Для получения уравнение касательной и нормали, нам нужно знать значение производной функции в заданной точке. Функция (П3) задана неявно. Поэтому применяем правило дифференцирования неявной функции. Для этого дифференцируем (П3) по x , считая, что y является функцией от x .
;
;
;
.
Отсюда
.

Находим производную в заданной точке, подставляя .
;
.

Находим уравнение касательной по формуле (2).
;
;
;
.

Находим уравнение нормали по формуле (3).
;
;
;
.

Касательная и нормаль к циссоиде изображены на рисунке ⇑.

Уравнение касательной: .
Уравнение нормали: .

Пример 4

Найти угол между кривыми и .

Найдем множество точек пересечения кривых, решая систему уравнений.

Левые части равны. Приравниваем правые части и выполняем преобразования.
;
(П4) .
Поскольку функция строго монотонна, то уравнение (П4) имеет один корень:
.
При . Кривые пересекаются в единственной точке . Обозначим ее как , где .

Введем обозначения для функций, с помощью которых заданы кривые:
.
Найдем их производные.
;
.
Найдем значения производных в точке , подставляя .
;
.

Ниже приводятся графики функций ⇓ и вывод формулы угла между кривыми.

Вывод формулы для угла между кривыми

Изложим вывод формулы (4). Для иллюстрации используем только что рассмотренный пример ⇑, в котором .

Рассмотрим две кривые, заданные уравнениями и , и пересекающиеся в некоторой точке . Докажем, что угол между кривыми определяется по формуле (4):
, где .
Или ;
при .

Проведем касательные к графикам функций в точке . Углы, которые образуют касательные с осью x обозначим как и . За положительное направление выберем направление против часовой стрелки. На рисунке . Считаем, что значения углов принадлежат интервалам . Согласно геометрическому смыслу производной,
.

В аналитической геометрии принято, что угол φ между прямыми равен наименьшему значению угла между ними.
Если , то ;
если , то .
Таким образом величина угла φ между касательными может находиться только в пределах
(Ф2) .

На рисунке угол между лучами и больше 90°, а между лучами и – меньше. Поэтому .

При доказательстве мы будем использовать соотношение:
, которое выполняется при .
Тогда в силу (Ф2),
.
Случай мы рассмотрим отдельно.

1) Пусть .
Тогда угол между прямыми . И мы имеем:
.
В конце мы подставили (Ф1).

2) Пусть .
Тогда ; . Поэтому . Это можно записать так: . Также применим формулу: . В результате получаем:

.

Этот случай изображен на рисунке ⇑.

3) Пусть .
При этом касательные взаимно перпендикулярны, . В этом случае , что указано в (4).

Использованная литература:
П.Е. Данько, А.Г. Попов, Т.Я.Кожевникова. Высшая математика в упражнениях и задачах. Часть 1. Москва, Высшая школа, 1980.
Л.Д. Кудрявцев, А.Д. Кутасов, В.И. Чехлов, М.И. Шабунин. Сборник задач по математическому анализу. Том 1. Москва, Физматлит, 2003.

Автор: Олег Одинцов . Опубликовано: 30-06-2021

Касательная к графику функции в точке. Уравнение касательной. Геометрический смысл производной

Статья дает подробное разъяснение определений, геометрического смысла производной с графическими обозначениями. Будет рассмотрено уравнение касательной прямой с приведением примеров, найдено уравнения касательной к кривым 2 порядка.

Определения и понятия

Угол наклона прямой y = k x + b называется угол α , который отсчитывается от положительного направления оси о х к прямой y = k x + b в положительном направлении.

На рисунке направление о х обозначается при помощи зеленой стрелки и в виде зеленой дуги, а угол наклона при помощи красной дуги. Синяя линия относится к прямой.

Угловой коэффициент прямой y = k x + b называют числовым коэффициентом k .

Угловой коэффициент равняется тангенсу наклона прямой, иначе говоря k = t g α .

• Угол наклона прямой равняется 0 только при параллельности о х и угловом коэффициенте, равному нулю, потому как тангенс нуля равен 0 . Значит, вид уравнения будет y = b .
• Если угол наклона прямой y = k x + b острый, тогда выполняются условия 0 α π 2 или 0 ° α 90 ° . Отсюда имеем, что значение углового коэффициента k считается положительным числом, потому как значение тангенс удовлетворяет условию t g α > 0 , причем имеется возрастание графика.
• Если α = π 2 , тогда расположение прямой перпендикулярно о х . Равенство задается при помощи равенства x = c со значением с , являющимся действительным числом.
• Если угол наклона прямой y = k x + b тупой, то соответствует условиям π 2 α π или 90 ° α 180 ° , значение углового коэффициента k принимает отрицательное значение, а график убывает.

Определение 3

Секущей называют прямую, которая проходит через 2 точки функции f ( x ) . Иначе говоря, секущая – это прямая, которая проводится через любые две точки графика заданной функции.

По рисунку видно, что А В является секущей, а f ( x ) – черная кривая, α — красная дуга, означающая угол наклона секущей.

Когда угловой коэффициент прямой равняется тангенсу угла наклона, то видно, что тангенс из прямоугольного треугольника А В С можно найти по отношению противолежащего катета к прилежащему.

Получаем формулу для нахождения секущей вида:

k = t g α = B C A C = f ( x B ) — f x A x B — x A , где абсциссами точек А и В являются значения x A , x B , а f ( x A ) , f ( x B ) — это значения функции в этих точках.

Очевидно, что угловой коэффициент секущей определен при помощи равенства k = f ( x B ) — f ( x A ) x B — x A или k = f ( x A ) — f ( x B ) x A — x B , причем уравнение необходимо записать как y = f ( x B ) — f ( x A ) x B — x A · x — x A + f ( x A ) или
y = f ( x A ) — f ( x B ) x A — x B · x — x B + f ( x B ) .

Секущая делит график визуально на 3 части: слева от точки А , от А до В , справа от В . На располагаемом ниже рисунке видно, что имеются три секущие, которые считаются совпадающими, то есть задаются при помощи аналогичного уравнения.

По определению видно, что прямая и ее секущая в данном случае совпадают.

Секущая может множественно раз пересекать график заданной функции. Если имеется уравнение вида у = 0 для секущей, тогда количество точек пересечения с синусоидой бесконечно.

Касательная к графику функции f ( x ) в точке x 0 ; f ( x 0 ) называется прямая, проходящая через заданную точку x 0 ; f ( x 0 ) , с наличием отрезка, который имеет множество значений х , близких к x 0 .

Рассмотрим подробно на ниже приведенном примере. Тогда видно, что прямая, заданная функцией y = x + 1 , считается касательной к y = 2 x в точке с координатами ( 1 ; 2 ) . Для наглядности, необходимо рассмотреть графики с приближенными к ( 1 ; 2 ) значениями. Функция y = 2 x обозначена черным цветом, синяя линия – касательная, красная точка – точка пересечения.

Очевидно, что y = 2 x сливается с прямой у = х + 1 .

Для определения касательной следует рассмотреть поведение касательной А В при бесконечном приближении точки В к точке А . Для наглядности приведем рисунок.

Секущая А В , обозначенная при помощи синей линии, стремится к положению самой касательной, а угол наклона секущей α начнет стремиться к углу наклона самой касательной α x .

Касательной к графику функции y = f ( x ) в точке А считается предельное положение секущей А В при В стремящейся к А , то есть B → A .

Теперь перейдем к рассмотрению геометрического смысла производной функции в точке.

Геометрический смысл производной функции в точке

Перейдем к рассмотрению секущей А В для функции f ( x ) , где А и В с координатами x 0 , f ( x 0 ) и x 0 + ∆ x , f ( x 0 + ∆ x ) , а ∆ x обозначаем как приращение аргумента. Теперь функция примет вид ∆ y = ∆ f ( x ) = f ( x 0 + ∆ x ) — f ( ∆ x ) . Для наглядности приведем в пример рисунок.

Рассмотрим полученный прямоугольный треугольник А В С . Используем определение тангенса для решения, то есть получим отношение ∆ y ∆ x = t g α . Из определения касательной следует, что lim ∆ x → 0 ∆ y ∆ x = t g α x . По правилу производной в точке имеем, что производную f ( x ) в точке x 0 называют пределом отношений приращения функции к приращению аргумента, где ∆ x → 0 , тогда обозначим как f ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x .

Отсюда следует, что f ‘ ( x 0 ) = lim ∆ x → 0 ∆ y ∆ x = t g α x = k x , где k x обозначают в качестве углового коэффициента касательной.

То есть получаем, что f ’ ( x ) может существовать в точке x 0 причем как и касательная к заданному графику функции в точке касания равной x 0 , f 0 ( x 0 ) , где значение углового коэффициента касательной в точке равняется производной в точке x 0 . Тогда получаем, что k x = f ‘ ( x 0 ) .

Геометрический смысл производной функции в точке в том, что дается понятие существования касательной к графику в этой же точке.

Уравнение касательной прямой

Чтобы записать уравнение любой прямой на плоскости, необходимо иметь угловой коэффициент с точкой, через которую она проходит. Его обозначение принимается как x 0 при пересечении.

Уравнение касательной к графику функции y = f ( x ) в точке x 0 , f 0 ( x 0 ) принимает вид y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) .

Имеется в виду, что конечным значением производной f ‘ ( x 0 ) можно определить положение касательной, то есть вертикально при условии lim x → x 0 + 0 f ‘ ( x ) = ∞ и lim x → x 0 — 0 f ‘ ( x ) = ∞ или отсутствие вовсе при условии lim x → x 0 + 0 f ‘ ( x ) ≠ lim x → x 0 — 0 f ‘ ( x ) .

Расположение касательной зависит от значения ее углового коэффициента k x = f ‘ ( x 0 ) . При параллельности к оси о х получаем, что k k = 0 , при параллельности к о у — k x = ∞ , причем вид уравнения касательной x = x 0 возрастает при k x > 0 , убывает при k x 0 .

Произвести составление уравнения касательной к графику функции y = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 в точке с координатами ( 1 ; 3 ) с определением угла наклона.

Решение

По условию имеем, что функция определяется для всех действительных чисел. Получаем, что точка с координатами, заданными по условию, ( 1 ; 3 ) является точкой касания, тогда x 0 = — 1 , f ( x 0 ) = — 3 .

Необходимо найти производную в точке со значением — 1 . Получаем, что

y ‘ = e x + 1 + x 3 3 — 6 — 3 3 x — 17 — 3 3 ‘ = = e x + 1 ‘ + x 3 3 ‘ — 6 — 3 3 x ‘ — 17 — 3 3 ‘ = e x + 1 + x 2 — 6 — 3 3 y ‘ ( x 0 ) = y ‘ ( — 1 ) = e — 1 + 1 + — 1 2 — 6 — 3 3 = 3 3

Значение f ’ ( x ) в точке касания является угловым коэффициентом касательной, который равняется тангенсу наклона.

Тогда k x = t g α x = y ‘ ( x 0 ) = 3 3

Отсюда следует, что α x = a r c t g 3 3 = π 6

Ответ: уравнение касательной приобретает вид

y = f ‘ ( x 0 ) · x — x 0 + f ( x 0 ) y = 3 3 ( x + 1 ) — 3 y = 3 3 x — 9 — 3 3

Для наглядности приведем пример в графической иллюстрации.

Черный цвет используется для графика исходной функции, синий цвет – изображение касательной, красная точка – точка касания. Рисунок, располагаемый справа, показывает в увеличенном виде.

Выяснить наличие существования касательной к графику заданной функции
y = 3 · x — 1 5 + 1 в точке с координатами ( 1 ; 1 ) . Составить уравнение и определить угол наклона.

Решение

По условию имеем, что областью определения заданной функции считается множество всех действительных чисел.

Перейдем к нахождению производной

y ‘ = 3 · x — 1 5 + 1 ‘ = 3 · 1 5 · ( x — 1 ) 1 5 — 1 = 3 5 · 1 ( x — 1 ) 4 5

Если x 0 = 1 , тогда f ’ ( x ) не определена, но пределы записываются как lim x → 1 + 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( + 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ и lim x → 1 — 0 3 5 · 1 ( x — 1 ) 4 5 = 3 5 · 1 ( — 0 ) 4 5 = 3 5 · 1 + 0 = + ∞ , что означает существование вертикальной касательной в точке ( 1 ; 1 ) .

Ответ: уравнение примет вид х = 1 , где угол наклона будет равен π 2 .

Для наглядности изобразим графически.

Найти точки графика функции y = 1 15 x + 2 3 — 4 5 x 2 — 16 5 x — 26 5 + 3 x + 2 , где

1. Касательная не существует;
2. Касательная располагается параллельно о х ;
3. Касательная параллельна прямой y = 8 5 x + 4 .

Решение

Необходимо обратить внимание на область определения. По условию имеем, что функция определена на множестве всех действительных чисел. Раскрываем модуль и решаем систему с промежутками x ∈ — ∞ ; 2 и [ — 2 ; + ∞ ) . Получаем, что

y = — 1 15 x 3 + 18 x 2 + 105 x + 176 , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 , x ∈ [ — 2 ; + ∞ )

Необходимо продифференцировать функцию. Имеем, что

y ‘ = — 1 15 x 3 + 18 x 2 + 105 x + 176 ‘ , x ∈ — ∞ ; — 2 1 15 x 3 — 6 x 2 + 9 x + 12 ‘ , x ∈ [ — 2 ; + ∞ ) ⇔ y ‘ = — 1 5 ( x 2 + 12 x + 35 ) , x ∈ — ∞ ; — 2 1 5 x 2 — 4 x + 3 , x ∈ [ — 2 ; + ∞ )

Когда х = — 2 , тогда производная не существует, потому что односторонние пределы не равны в этой точке:

lim x → — 2 — 0 y ‘ ( x ) = lim x → — 2 — 0 — 1 5 ( x 2 + 12 x + 35 = — 1 5 ( — 2 ) 2 + 12 ( — 2 ) + 35 = — 3 lim x → — 2 + 0 y ‘ ( x ) = lim x → — 2 + 0 1 5 ( x 2 — 4 x + 3 ) = 1 5 — 2 2 — 4 — 2 + 3 = 3

Вычисляем значение функции в точке х = — 2 , где получаем, что

1. y ( — 2 ) = 1 15 — 2 + 2 3 — 4 5 ( — 2 ) 2 — 16 5 ( — 2 ) — 26 5 + 3 — 2 + 2 = — 2 , то есть касательная в точке ( — 2 ; — 2 ) не будет существовать.
2. Касательная параллельна о х , когда угловой коэффициент равняется нулю. Тогда k x = t g α x = f ‘ ( x 0 ) . То есть необходимо найти значения таких х , когда производная функции обращает ее в ноль. То есть значения f ’ ( x ) и будут являться точками касания, где касательная является параллельной о х .

Когда x ∈ — ∞ ; — 2 , тогда — 1 5 ( x 2 + 12 x + 35 ) = 0 , а при x ∈ ( — 2 ; + ∞ ) получаем 1 5 ( x 2 — 4 x + 3 ) = 0 .

— 1 5 ( x 2 + 12 x + 35 ) = 0 D = 12 2 — 4 · 35 = 144 — 140 = 4 x 1 = — 12 + 4 2 = — 5 ∈ — ∞ ; — 2 x 2 = — 12 — 4 2 = — 7 ∈ — ∞ ; — 2 1 5 ( x 2 — 4 x + 3 ) = 0 D = 4 2 — 4 · 3 = 4 x 3 = 4 — 4 2 = 1 ∈ — 2 ; + ∞ x 4 = 4 + 4 2 = 3 ∈ — 2 ; + ∞

Вычисляем соответствующие значения функции

y 1 = y — 5 = 1 15 — 5 + 2 3 — 4 5 — 5 2 — 16 5 — 5 — 26 5 + 3 — 5 + 2 = 8 5 y 2 = y ( — 7 ) = 1 15 — 7 + 2 3 — 4 5 ( — 7 ) 2 — 16 5 — 7 — 26 5 + 3 — 7 + 2 = 4 3 y 3 = y ( 1 ) = 1 15 1 + 2 3 — 4 5 · 1 2 — 16 5 · 1 — 26 5 + 3 1 + 2 = 8 5 y 4 = y ( 3 ) = 1 15 3 + 2 3 — 4 5 · 3 2 — 16 5 · 3 — 26 5 + 3 3 + 2 = 4 3

Отсюда — 5 ; 8 5 , — 4 ; 4 3 , 1 ; 8 5 , 3 ; 4 3 считаются искомыми точками графика функции.

Рассмотрим графическое изображение решения.

Черная линия – график функции, красные точки – точки касания.

1. Когда прямые располагаются параллельно, то угловые коэффициенты равны. Тогда необходимо заняться поиском точек графика функции, где угловой коэффициент будет равняться значению 8 5 . Для этого нужно решить уравнение вида y ‘ ( x ) = 8 5 . Тогда, если x ∈ — ∞ ; — 2 , получаем, что — 1 5 ( x 2 + 12 x + 35 ) = 8 5 , а если x ∈ ( — 2 ; + ∞ ) , тогда 1 5 ( x 2 — 4 x + 3 ) = 8 5 .

Первое уравнение не имеет корней, так как дискриминант меньше нуля. Запишем, что

— 1 5 x 2 + 12 x + 35 = 8 5 x 2 + 12 x + 43 = 0 D = 12 2 — 4 · 43 = — 28 0

Другое уравнение имеет два действительных корня, тогда

1 5 ( x 2 — 4 x + 3 ) = 8 5 x 2 — 4 x — 5 = 0 D = 4 2 — 4 · ( — 5 ) = 36 x 1 = 4 — 36 2 = — 1 ∈ — 2 ; + ∞ x 2 = 4 + 36 2 = 5 ∈ — 2 ; + ∞

Перейдем к нахождению значений функции. Получаем, что

y 1 = y ( — 1 ) = 1 15 — 1 + 2 3 — 4 5 ( — 1 ) 2 — 16 5 ( — 1 ) — 26 5 + 3 — 1 + 2 = 4 15 y 2 = y ( 5 ) = 1 15 5 + 2 3 — 4 5 · 5 2 — 16 5 · 5 — 26 5 + 3 5 + 2 = 8 3

Точки со значениями — 1 ; 4 15 , 5 ; 8 3 являются точками, в которых касательные параллельны прямой y = 8 5 x + 4 .

Ответ: черная линия – график функции, красная линия – график y = 8 5 x + 4 , синяя линия – касательные в точках — 1 ; 4 15 , 5 ; 8 3 .

Возможно существование бесконечного количества касательных для заданных функций.

Написать уравнения всех имеющихся касательных функции y = 3 cos 3 2 x — π 4 — 1 3 , которые располагаются перпендикулярно прямой y = — 2 x + 1 2 .

Решение

Для составления уравнения касательной необходимо найти коэффициент и координаты точки касания, исходя из условия перпендикулярности прямых. Определение звучит так: произведение угловых коэффициентов, которые перпендикулярны прямым, равняется — 1 , то есть записывается как k x · k ⊥ = — 1 . Из условия имеем, что угловой коэффициент располагается перпендикулярно прямой и равняется k ⊥ = — 2 , тогда k x = — 1 k ⊥ = — 1 — 2 = 1 2 .

Теперь необходимо найти координаты точек касания. Нужно найти х , после чего его значение для заданной функции. Отметим, что из геометрического смысла производной в точке
x 0 получаем, что k x = y ‘ ( x 0 ) . Из данного равенства найдем значения х для точек касания.

y ‘ ( x 0 ) = 3 cos 3 2 x 0 — π 4 — 1 3 ‘ = 3 · — sin 3 2 x 0 — π 4 · 3 2 x 0 — π 4 ‘ = = — 3 · sin 3 2 x 0 — π 4 · 3 2 = — 9 2 · sin 3 2 x 0 — π 4 ⇒ k x = y ‘ ( x 0 ) ⇔ — 9 2 · sin 3 2 x 0 — π 4 = 1 2 ⇒ sin 3 2 x 0 — π 4 = — 1 9

Это тригонометрическое уравнение будет использовано для вычисления ординат точек касания.

3 2 x 0 — π 4 = a r c sin — 1 9 + 2 πk или 3 2 x 0 — π 4 = π — a r c sin — 1 9 + 2 πk

3 2 x 0 — π 4 = — a r c sin 1 9 + 2 πk или 3 2 x 0 — π 4 = π + a r c sin 1 9 + 2 πk

x 0 = 2 3 π 4 — a r c sin 1 9 + 2 πk или x 0 = 2 3 5 π 4 + a r c sin 1 9 + 2 πk , k ∈ Z

Z — множество целых чисел.

Найдены х точек касания. Теперь необходимо перейти к поиску значений у :

y 0 = 3 cos 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — sin 2 3 2 x 0 — π 4 — 1 3 или y 0 = 3 · — 1 — sin 2 3 2 x 0 — π 4 — 1 3

y 0 = 3 · 1 — — 1 9 2 — 1 3 или y 0 = 3 · — 1 — — 1 9 2 — 1 3

y 0 = 4 5 — 1 3 или y 0 = — 4 5 + 1 3

Отсюда получаем, что 2 3 π 4 — a r c sin 1 9 + 2 πk ; 4 5 — 1 3 , 2 3 5 π 4 + a r c sin 1 9 + 2 πk ; — 4 5 + 1 3 являются точками касания.

Ответ: необходимы уравнения запишутся как

y = 1 2 x — 2 3 π 4 — a r c sin 1 9 + 2 πk + 4 5 — 1 3 , y = 1 2 x — 2 3 5 π 4 + a r c sin 1 9 + 2 πk — 4 5 + 1 3 , k ∈ Z

Для наглядного изображения рассмотрим функцию и касательную на координатной прямой.

Рисунок показывает, что расположение функции идет на промежутке [ — 10 ; 10 ] , где черная прямя – график функции, синие линии – касательные, которые располагаются перпендикулярно заданной прямой вида y = — 2 x + 1 2 . Красные точки – это точки касания.

Касательная к окружности, эллипсу, гиперболе, параболе

Канонические уравнения кривых 2 порядка не являются однозначными функциями. Уравнения касательных для них составляются по известным схемам.

Касательная к окружности

Для задания окружности с центром в точке x c e n t e r ; y c e n t e r и радиусом R применяется формула x — x c e n t e r 2 + y — y c e n t e r 2 = R 2 .

Данное равенство может быть записано как объединение двух функций:

y = R 2 — x — x c e n t e r 2 + y c e n t e r y = — R 2 — x — x c e n t e r 2 + y c e n t e r

Первая функция располагается вверху, а вторая внизу, как показано на рисунке.

Для составления уравнения окружности в точке x 0 ; y 0 , которая располагается в верхней или нижней полуокружности, следует найти уравнение графика функции вида y = R 2 — x — x c e n t e r 2 + y c e n t e r или y = — R 2 — x — x c e n t e r 2 + y c e n t e r в указанной точке.

Когда в точках x c e n t e r ; y c e n t e r + R и x c e n t e r ; y c e n t e r — R касательные могут быть заданы уравнениями y = y c e n t e r + R и y = y c e n t e r — R , а в точках x c e n t e r + R ; y c e n t e r и
x c e n t e r — R ; y c e n t e r будут являться параллельными о у , тогда получим уравнения вида x = x c e n t e r + R и x = x c e n t e r — R .

Касательная к эллипсу

Когда эллипс имеет центр в точке x c e n t e r ; y c e n t e r с полуосями a и b , тогда он может быть задан при помощи уравнения x — x c e n t e r 2 a 2 + y — y c e n t e r 2 b 2 = 1 .

Эллипс и окружность могут быть обозначаться при помощи объединения двух функций, а именно: верхнего и нижнего полуэллипса. Тогда получаем, что

y = b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r y = — b a · a 2 — ( x — x c e n t e r ) 2 + y c e n t e r

Если касательные располагаются на вершинах эллипса, тогда они параллельны о х или о у . Ниже для наглядности рассмотрим рисунок.

Написать уравнение касательной к эллипсу x — 3 2 4 + y — 5 2 25 = 1 в точках со значениями x равного х = 2 .

Решение

Необходимо найти точки касания, которые соответствуют значению х = 2 . Производим подстановку в имеющееся уравнение эллипса и получаем, что

x — 3 2 4 x = 2 + y — 5 2 25 = 1 1 4 + y — 5 2 25 = 1 ⇒ y — 5 2 = 3 4 · 25 ⇒ y = ± 5 3 2 + 5

Тогда 2 ; 5 3 2 + 5 и 2 ; — 5 3 2 + 5 являются точками касания, которые принадлежат верхнему и нижнему полуэллипсу.

Перейдем к нахождению и разрешению уравнения эллипса относительно y . Получим, что

x — 3 2 4 + y — 5 2 25 = 1 y — 5 2 25 = 1 — x — 3 2 4 ( y — 5 ) 2 = 25 · 1 — x — 3 2 4 y — 5 = ± 5 · 1 — x — 3 2 4 y = 5 ± 5 2 4 — x — 3 2

Очевидно, что верхний полуэллипс задается с помощью функции вида y = 5 + 5 2 4 — x — 3 2 , а нижний y = 5 — 5 2 4 — x — 3 2 .

Применим стандартный алгоритм для того, чтобы составить уравнение касательной к графику функции в точке. Запишем, что уравнение для первой касательной в точке 2 ; 5 3 2 + 5 будет иметь вид

y ‘ = 5 + 5 2 4 — x — 3 2 ‘ = 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = — 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = — 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = 5 2 3 ( x — 2 ) + 5 3 2 + 5

Получаем, что уравнение второй касательной со значением в точке
2 ; — 5 3 2 + 5 принимает вид

y ‘ = 5 — 5 2 4 — ( x — 3 ) 2 ‘ = — 5 2 · 1 2 4 — ( x — 3 ) 2 · 4 — ( x — 3 ) 2 ‘ = = 5 2 · x — 3 4 — ( x — 3 ) 2 ⇒ y ‘ ( x 0 ) = y ‘ ( 2 ) = 5 2 · 2 — 3 4 — ( 2 — 3 ) 2 = — 5 2 3 ⇒ y = y ‘ ( x 0 ) · x — x 0 + y 0 ⇔ y = — 5 2 3 ( x — 2 ) — 5 3 2 + 5

Графически касательные обозначаются так:

Касательная к гиперболе

Когда гипербола имеет центр в точке x c e n t e r ; y c e n t e r и вершины x c e n t e r + α ; y c e n t e r и x c e n t e r — α ; y c e n t e r , имеет место задание неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = 1 , если с вершинами x c e n t e r ; y c e n t e r + b и x c e n t e r ; y c e n t e r — b , тогда задается при помощи неравенства x — x c e n t e r 2 α 2 — y — y c e n t e r 2 b 2 = — 1 .

Гипербола может быть представлена в виде двух объединенных функций вида

y = b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 — a 2 + y c e n t e r или y = b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r y = — b a · ( x — x c e n t e r ) 2 + a 2 + y c e n t e r

В первом случае имеем, что касательные параллельны о у , а во втором параллельны о х .

Отсюда следует, что для того, чтобы найти уравнение касательной к гиперболе, необходимо выяснить, какой функции принадлежит точка касания. Чтобы определить это, необходимо произвести подстановку в уравнения и проверить их на тождественность.

Составить уравнение касательной к гиперболе x — 3 2 4 — y + 3 2 9 = 1 в точке 7 ; — 3 3 — 3 .

Решение

Необходимо преобразовать запись решения нахождения гиперболы при помощи 2 функций. Получим, что

x — 3 2 4 — y + 3 2 9 = 1 ⇒ y + 3 2 9 = x — 3 2 4 — 1 ⇒ y + 3 2 = 9 · x — 3 2 4 — 1 ⇒ y + 3 = 3 2 · x — 3 2 — 4 и л и y + 3 = — 3 2 · x — 3 2 — 4 ⇒ y = 3 2 · x — 3 2 — 4 — 3 y = — 3 2 · x — 3 2 — 4 — 3

Необходимо выявить, к какой функции принадлежит заданная точка с координатами 7 ; — 3 3 — 3 .

Очевидно, что для проверки первой функции необходимо y ( 7 ) = 3 2 · ( 7 — 3 ) 2 — 4 — 3 = 3 3 — 3 ≠ — 3 3 — 3 , тогда точка графику не принадлежит, так как равенство не выполняется.

Для второй функции имеем, что y ( 7 ) = — 3 2 · ( 7 — 3 ) 2 — 4 — 3 = — 3 3 — 3 ≠ — 3 3 — 3 , значит, точка принадлежит заданному графику. Отсюда следует найти угловой коэффициент.

y ‘ = — 3 2 · ( x — 3 ) 2 — 4 — 3 ‘ = — 3 2 · x — 3 ( x — 3 ) 2 — 4 ⇒ k x = y ‘ ( x 0 ) = — 3 2 · x 0 — 3 x 0 — 3 2 — 4 x 0 = 7 = — 3 2 · 7 — 3 7 — 3 2 — 4 = — 3

Ответ: уравнение касательной можно представить как

y = — 3 · x — 7 — 3 3 — 3 = — 3 · x + 4 3 — 3

Наглядно изображается так:

Касательная к параболе

Чтобы составить уравнение касательной к параболе y = a x 2 + b x + c в точке x 0 , y ( x 0 ) , необходимо использовать стандартный алгоритм, тогда уравнение примет вид y = y ‘ ( x 0 ) · x — x 0 + y ( x 0 ) . Такая касательная в вершине параллельна о х .

Следует задать параболу x = a y 2 + b y + c как объединение двух функций. Поэтому нужно разрешить уравнение относительно у . Получаем, что

x = a y 2 + b y + c ⇔ a y 2 + b y + c — x = 0 D = b 2 — 4 a ( c — x ) y = — b + b 2 — 4 a ( c — x ) 2 a y = — b — b 2 — 4 a ( c — x ) 2 a

Графически изобразим как:

Для выяснения принадлежности точки x 0 , y ( x 0 ) функции, нежно действовать по стандартному алгоритму. Такая касательная будет параллельна о у относительно параболы.

Написать уравнение касательной к графику x — 2 y 2 — 5 y + 3 , когда имеем угол наклона касательной 150 ° .

Решение

Начинаем решение с представления параболы в качестве двух функций. Получим, что

— 2 y 2 — 5 y + 3 — x = 0 D = ( — 5 ) 2 — 4 · ( — 2 ) · ( 3 — x ) = 49 — 8 x y = 5 + 49 — 8 x — 4 y = 5 — 49 — 8 x — 4

Значение углового коэффициента равняется значению производной в точке x 0 этой функции и равняется тангенсу угла наклона.

k x = y ‘ ( x 0 ) = t g α x = t g 150 ° = — 1 3

Отсюда определим значение х для точек касания.

Первая функция запишется как

y ‘ = 5 + 49 — 8 x — 4 ‘ = 1 49 — 8 x ⇒ y ‘ ( x 0 ) = 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3

Очевидно, что действительных корней нет, так как получили отрицательное значение. Делаем вывод, что касательной с углом 150 ° для такой функции не существует.

Вторая функция запишется как

y ‘ = 5 — 49 — 8 x — 4 ‘ = — 1 49 — 8 x ⇒ y ‘ ( x 0 ) = — 1 49 — 8 x 0 = — 1 3 ⇔ 49 — 8 x 0 = — 3 x 0 = 23 4 ⇒ y ( x 0 ) = 5 — 49 — 8 · 23 4 — 4 = — 5 + 3 4

Имеем, что точки касания — 23 4 ; — 5 + 3 4 .

Ответ: уравнение касательной принимает вид

п.1. Уравнение касательной

Рассмотрим кривую (y=f(x)).
Выберем на ней точку A с координатами ((x_0,y_0)), проведем касательную AB в этой точке.

Как было показано в §42 данного справочника, угловой коэффициент касательной равен производной от функции f в точке (x_0): $$ k=f'(x_0) $$ Уравнение прямой AB, проведенной через две точки: ((y_B-y_A)=k(x_B-x_A)).
Для (A(x_0,y_0), B(x,y)) получаем: begin{gather*} (y-y_0)=k(x-x_0)\ y=k(x-x_0)+y_0\ y=f'(x_0)(x-x_0)+f(x_0) end{gather*}

Уравнение касательной к кривой (y=f(x)) в точке (x_0) имеет вид: $$ y=f'(x_0)(x-x_0)+f(x_0) $$ при условии, что производная (f'(x_0)=aneinfty) — существует и конечна.

Чтобы записать уравнение касательной с угловым коэффициентом в виде (y=kx+b), нужно раскрыть скобки и привести подобные: $$ y=f'(x_0)(x-x_0)+f(x_0)=underbrace{f'(x_0)}_{=k}x+underbrace{f(x_0)-f'(x_0)cdot x_0}_{=b} $$

Уравнение касательной с угловым коэффициентом: begin{gather*} y=kx+b\ k=f'(x_0), b=f(x_0)-f'(x_0)cdot x_0 end{gather*}

п.2. Алгоритм построения касательной

п.3. Вертикальная касательная

В случае, если производная (f'(x_0)=pminfty) — существует, но бесконечна, в точке (x_0) проходит вертикальная касательная (x=x_0).

п.4. Примеры

Пример 1. Для функции (f(x)=2x^2+4x)
a) напишите уравнения касательных, проведенных к графику функции в точках его пересечения с осью OX.

б) Найдите, в какой точке касательная образует с положительным направлением оси OX угол 45°. Напишите уравнение этой касательной.

в) найдите, в какой точке касательная будет параллельна прямой (2x+y-6=0). Напишите уравнение этой касательной.

г) в какой точке функции можно провести горизонтальную касательную? Напишите уравнение этой касательной.

Ответ: а) (y=4x) и (y=-4x-8); б) (y=x-frac98); в) (2x+y+frac92=0); г) (y=-2)

Пример 2. Напишите уравнение касательной к графику функции в заданной точке:
a) ( f(x)=frac5x+frac x5, x_0=4 ) begin{gather*} f(x_0)=frac54+frac45=frac{25+16}{20}=frac{41}{20}\ f'(x)=left(frac5xright)’+left(frac x5right)’=-frac{5}{x^2}+frac15=frac{-25+x^2}{5x^2}=frac{x^2-25}{5x^2}\ f'(x_0)=frac{4^2-25}{5cdot 4^2}=-frac{9}{80} end{gather*} Уравнение касательной: $$ y=-frac{9}{80}(x-4)+frac{41}{20}=-frac{9}{80}x+frac{9}{20}+frac{41}{20}=-frac{9}{80}x+2,5 $$
б) ( f(x)=frac{x^2+5}{3-x}, x_0=2 ) begin{gather*} f(x_0)=frac{2^2+5}{3-2}=frac91=9\ f'(x)=frac{(x^2+5)'(3-x)-(x^2+5)(3-x)’}{(3-x)^2}=frac{2x(3-x)+(x^2+5)}{(3-x)^2}=\ =frac{6x-2x^2+x^2+5}{(3-x)^2}=frac{-x^2+6x+5}{(3-x)^2}\ f'(x_0)=frac{-2^2+6cdot 2+5}{(3-2)^2}=13 end{gather*} Уравнение касательной: $$ y=13(x-2)+9=13x-26+9=13x-17 $$

Уравнение перпендикуляра: (y=-frac x2).
Находим точку пересечения прямой (y=2x-1) и перпендикуляра (y=-frac x2): begin{gather*} 2x-1=-frac x2Rightarrow 2,5x=1Rightarrow x=0,4; y=-frac{0,4}{2}=-0,2 end{gather*} Точка пересечения A(0,4;-0,2).
Находим расстояние (OA=sqrt{0,4^2+(-0,2)^2}=0,2sqrt{2^2+1^2}=frac{sqrt{5}}{5})
Ответ: (frac{sqrt{5}}{5})