Как найти угол квадрата формула - Исправление недочетов и поиск решений вместе с Examum.ru

Из Евклидовой геометрии известно, что сумма углов многоугольника равна 180*(n-2), где n-число углов. Поскольку квадрат имеет четыре угла, то сумма углов квадрата равна 180*(4-2)=360 градусов. Все углы квадрата равны, так что величина одного угла квадрата равна 360/4=90 градусов.

Это простое доказательство, однако еще проще запомнить, что квадрат — это четырехугольник, у которого все углы прямые, то есть равны 90 градусов.

автор вопроса выбрал этот ответ лучшим

Прямоугольник на плоскости с равными сторонами является квадратом и все углы(всего четыре) у него прямые.

Любой угол в таком квадрате равен 90 градусам.

В Неевклидовой геометрии требования к квадрату не такие жесткие — это всего-лишь четырехугольник, у которого равные стороны и углы не обязательно 90 градусов, а могут быть больше или меньше (главное, чтобы все они были равны между собой) и в зависимости от того, на какой поверхности расположен этот квадрат — выпуклой или вогнутой, эти углы могут иметь разные величины.

Величина углов в таких квадратах может быть разной, например 120 градусов, 72 градуса

gudroni
[35.8K]

8 лет назад

Угол в квадрате равен девяносто градусам. Если вы конечно имеете виду именно это. Странно, что вы вообще об этом спрашиваете, ведь это слишком очевидные вещи, которым учат с младших классов, и такую информацию знает каждый.

Galina7v7
[120K]

5 месяцев назад

Угол при вершине, причём любой в квадрате равен 90 градусам. Квадрат это правильная фигура, в которой все стороны равны между собой, а все углы тоже равны и равны 90 градусам.

Сумма углов любого четырёхугольника равна 180 градусам, а учитывая, что углов 4 и они равны между собой, то каждый из углов равен 90 градусам.

Вся сумма углов у квадрата всегда будет равна полной окружности, т.е. 360 градусов, а раз в квадрате все стороны одинаковые и углы тогда тоже одинаковые, так как они прямые, не будь тогда эта геометрическая фигура квадратом, то сумму всех углов надо разделить поровну, т.е. 360/4=90

Итак это 90 градусов…

Polerol
[27.8K]

8 лет назад

Квадрат — это по определению такая геометрическая фигура, в которой все углы одинаковы и равны 90 градусов. Это определение надо просто запомнить. Еще, если возникнет сомнение чему же равен угол в квадрате, можно вспомнить что сумма всех его углов это 360, делим на 4 и получаем те же 90 градусов.

Смотря, каков исходный угол. Если он равен, например, 30 градусов, то в квадрате это будет 900 градусов. Так как 30^2=900. Соответственно, 90 градусов в квадрате это 8100. И так далее. Только, обычно в квадрат возводят не сами углы, а их тригонометрические функции.

Delledi
[18.5K]

8 лет назад

Квадрат — это фигура стороны и углы которого все равны. Угол в квадрате составляет 90 градусов. Этот вопрос так же есть в игре Школа Аватарии в разделе математика и из предложенных вариантов ответов нужно выбрать правильный — угол квадрата равен 90 ГРАДУСОВ,

Leather-Radish
[65.1K]

8 лет назад

Квадрат — это фигура, которая состоит из четырех сторон, каждая из которых равна и примыкает к другой стороне под углом в 90 градусов. Правильным ответом на игровой вопрос «Школа Аватарии», в разделе «математика» следует считать ответ: 90 градусов.

Агафья
[118K]

8 лет назад

Квадрат потому и называется квадратом, что все углы у него одинаковой величины и составляют 90 градусов. Квадрат представляет собой частный вид прямоугольника, где из названия видно, что все углы в нём прямые, то есть 90 градусов.

Leona-100
[110K]

8 лет назад

Из школьного курса геометрии мы знаем, что угол в квадрате будет равен 90 градусам. Все углы в сумме дают 360 градусов. Так как в квадрате 4 угла, делим 360 градусов на 4 и получаем 90 градусов. Это и будет правильным ответом.

Сумма углов любого прямоугольника — 360 градусов. Отсюда, зная, что углов у квадрата четыре и все они равны, делим 360 на 4, получаем 90 градусов. Это и будет ответом на вопрос о величине угла в квадрате — 90 градусов.

GREENka
[1.9K]

8 лет назад

90 градусов.все углы равны. углы прямые. в сумме дают 360 градусов.

Дендра
[3.1K]

8 лет назад

90 градусов, 100 градов, пи пополам радианов.

Знаете ответ?

Смотрите также:

Чему равен угол ∠B в треугольнике ∆ABC, если (см)?

Внутри треугольника расположены два квадрата (см.). Чему равен угол α?

Чему равен угол ∠A в треугольнике ∆AED, если (см)?

Чему равен угол ∠ОАЕ, если конверт вписан в окружность (см)?

Чему равен угол Y, если A=36°, а B=50°+50° (см)?

Чему равен угол ∠A, если углы ∠B и ∠C равны 37° и 23° (см)?

Дан треугольник ABC, где 2BC=AC и угол C=74°, (см). Чему равен угол CDF?

Правильный пятиугольник, правильный треугольник и …(см) Чем равен угол х?

Стереометрия. Чему равен угол между ромбом и параллелограммом?

Чему равен угол α между касательными, проведенными к окружностям (см.ниже)?

Источник

Квадрат. Формулы и свойства квадрата

Определение.

Квадрат — это четырехугольник у которого все четыре стороны и углы одинаковы.
Квадраты отличаются между собой только длиной стороны, но все четыре угла у них прямые, то есть по 90°.

Основные свойства квадрата

Квадратом также могут быть параллелограмм, ромб или прямоугольник если они имеют одинаковые длины диагоналей, сторон и одинаковые углы.

1. Все четыре стороны квадрата имеют одинаковую длину, то есть они равны:

AB = BC = CD = AD

2. Противоположные стороны квадрата параллельны:

AB||CD, BC||AD

3. Все четыре угла квадрата прямые:

∠ABC = ∠BCD = ∠CDA = ∠DAB = 90°

4. Сумма углов квадрата равна 360 градусов:

∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°

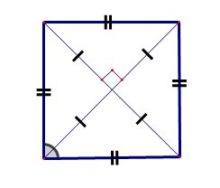
5. Диагонали квадрата имеют одинаковой длины:

AC = BD

6. Каждая диагональ квадрата делит квадрат на две одинаковые симметричные фигуры

7. Диагонали квадрата пересекаются под прямым углом, и разделяют друг друга пополам:

AC┴BD		AO = BO = CO = DO =	d
2

8. Точка пересечения диагоналей называется центром квадрата и также является центром вписанной и описанной окружности

9. Каждая диагональ делит угол квадрата пополам, то есть они являются биссектрисами углов квадрата:

ΔABC = ΔADC = ΔBAD = ΔBCD
∠ACB = ∠ACD = ∠BDC = ∠BDA = ∠CAB = ∠CAD = ∠DBC = ∠DBA = 45°

10. Обе диагонали разделяют квадрат на четыре равные треугольника, причем эти треугольники одновременно и равнобедренные и прямоугольные:

ΔAOB = ΔBOC = ΔCOD = ΔDOA

Диагональ квадрата

Определение.

Диагональю квадрата называется любой отрезок, соединяющий две вершины противоположных углов квадрата.

Диагональ любого квадрата всегда больше его стороны в√2 раз.

Формулы определения длины диагонали квадрата

1. Формула диагонали квадрата через сторону квадрата:

d = a·√2

2. Формула диагонали квадрата через площадь квадрата:

d = √2S

3. Формула диагонали квадрата через периметр квадрата:

4. Формула диагонали квадрата через радиус описанной окружности:

d = 2R

5. Формула диагонали квадрата через диаметр описанной окружности:

d = D_о

6. Формула диагонали квадрата через радиус вписанной окружности:

d = 2r√2

7. Формула диагонали квадрата через диаметр вписанной окружности:

d = D_в√2

8. Формула диагонали квадрата через длину отрезка l:

Периметр квадрата

Определение.

Периметром квадрата называется сумма длин всех сторон квадрата.

Формулы определения длины периметра квадрата

1. Формула периметра квадрата через сторону квадрата:

P = 4a

2. Формула периметра квадрата через площадь квадрата:

P = 4√S

3. Формула периметра квадрата через диагональ квадрата:

P = 2d√2

4. Формула периметра квадрата через радиус описанной окружности:

P = 4R√2

5. Формула периметра квадрата через диаметр описанной окружности:

P = 2D_о√2

6. Формула периметра квадрата через радиус вписанной окружности:

P = 8r

7. Формула периметра квадрата через диаметр вписанной окружности:

P = 4D_в

8. Формула периметра квадрата через длину отрезка l:

Площадь квадрата

Определение.

Площадью квадрата называется пространство, ограниченное сторонами квадрата, то есть в пределах периметра квадрата.

Площадь квадрата больше площади любого четырехугольника с таким же периметром.

Формулы определения площади квадрата

1. Формула площади квадрата через сторону квадрата:

S = a²

2. Формула площади квадрата через периметр квадрата:

3. Формула площади квадрата через диагональ квадрата:

4. Формула площади квадрата через радиус описанной окружности:

S = 2R²

5. Формула площади квадрата через диаметр описанной окружности:

6. Формула площади квадрата через радиус вписанной окружности:

S = 4r²

7. Формула площади квадрата через диаметр вписанной окружности:

S = D_в²

8. Формула площади квадрата через длину отрезка l:

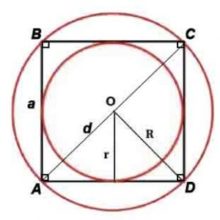
Окружность описанная вокруг квадрата

Определение.

Кругом описанным вокруг квадрата называется круг проходящий через четыре вершины квадрата и имеющий центр на пересечении диагоналей квадрата.

Радиус окружности описанной вокруг квадрата всегда больше радиуса вписанной окружности в√2 раз.

Радиус окружности описанной вокруг квадрата равен половине диагонали.

Площадь круга описанного вокруг квадрата большая площадь того же квадрата в π/2 раз.

Формулы определения радиуса окружности описанной вокруг квадрата

1. Формула радиуса окружности описанной вокруг квадрата через сторону квадрата:

2. Формула радиуса окружности описанной вокруг квадрата через периметр квадрата:

3. Формула радиуса окружности описанной вокруг квадрата через площадь квадрата:

4. Формула радиуса круга описанного вокруг квадрата через диагональ квадрата:

5. Формула радиуса круга описанного вокруг квадрата через диаметр описанной окружности:

6. Формула радиуса круга описанного вокруг квадрата через радиус вписанной окружности:

R = r √2

7. Формула радиуса круга описанного вокруг квадрата через диаметр вписанной окружности:

8. формула радиуса круга описанного вокруг квадрата через длину отрезка l:

Окружность вписанная в квадрата

Определение.

Кругом вписанным в квадрат называется круг, который примыкает к серединам сторон квадрата и имеет центр на пересечении диагоналей квадрата.

Радиус вписанной окружности равен половине стороны квадрата.

Площадь круга вписанного в квадрат меньше площади квадрата в 4/π раза.

Формулы определения радиуса круга вписанного в квадрат

1. Формула радиуса круга вписанного в квадрат через сторону квадрата:

2. Формула радиуса круга вписанного в квадрат через диагональ квадрата:

3. Формула радиуса круга вписанного в квадрат через периметр квадрата:

4. Формула радиуса круга вписанного в квадрат через площадь квадрата:

5. Формула радиуса круга вписанного в квадрат через радиус описанной окружности:

6. Формула радиуса круга вписанного в квадрат через диаметр, описанной окружности:

7 Формула радиуса круга вписанного в квадрат через диаметр вписанной окружности:

8. Формула радиуса круга вписанного в квадрат через длину отрезка l:

Источник

Квадрат — это прямоугольник, у которого равны все стороны и все внутренние углы. У квадрата четыре стороны и четыре внутренних угла. А это означает, что надо поделить 360 градусов на 4 и получится величина внутреннего угла, равная 90^о.

Если величину выражать в радианах, то величина внутреннего угла равна (pi/2). Если же вас интересует внешний угол, то он будет равен 360-90=270^о. Или в радианах (2pi-pi/2=3pi/2) радиан. Еще углы квадрата называют прямыми. Когда задают вопрос — чему равен угол в квадрате, то речь также может идти о о центральном угле (угол с вершиной в центре квадрата и сторонами угла, идущими к вершинам). Такой угол тоже равен девяносто градусов. Но, скорее всего вас интересует все таки величина внутреннего угла при вершине квадрата, поэтому на вопрос: чему равен угол в квадрате самый надежный ответ: угол в квадрате равен 90^о. Если у вас возникают вопросы — задавайте их в комментариях к этой публикации.

Похожие публикации: угол, квадрат, математика

Источник

Квадрат — определение и свойства

Квадрат — это прямоугольник, у которого все стороны равны.
Можно дать и другое определение квадрата:
квадрат — это ромб, у которого все углы прямые.

Получается, что квадрат обладает всеми свойствами параллелограмма, прямоугольника и ромба.

Квадрат относится к правильным многоугольникам. У правильного многоугольника все стороны равны и все углы равны.

Перечислим свойства квадрата:

Все углы квадрата — прямые, все стороны квадрата — равны.

$angle A= angle B=angle C=angle D=90^{circ }.$
Диагонали квадрата равны и пересекаются под прямым углом.
Диагонали квадрата делятся точкой пересечения пополам.
Диагонали квадрата являются биссектрисами его углов (делят его углы пополам).
Диагонали квадрата делят его на 4 равных прямоугольных равнобедренных треугольника:

Периметр квадрата P в 4 раза больше его стороны и равен: P=4a.

Площадь квадрата равна квадрату его стороны: S=a^2 .

Теорема 1. Диагональ квадрата равна произведению его стороны на sqrt{2} , то есть
.

Доказательство:

Рассмотрим квадрат ABCD. Проведем диагональ квадрата AC.

Треугольник АВС – прямоугольный с гипотенузой АС. Запишем для треугольника АВС теорему Пифагора:

$AC^{2}=AB^{2}+BC^{2};$

$AC^{2}=a^{2}+a^{2}=2a^{2}, AC=asqrt{2},$ что и требовалось доказать.

Теорема 2. Радиус вписанной в квадрат окружности равен половине его стороны:

$displaystyle r=frac{1}{2}cdot a$

Доказательство:

Пусть окружность с центром в точке О и радиусом r вписана в квадрат АВСD и касается его сторон в точках
P, M, N, K.

Тогда поскольку AB параллельно CD. Через точку О можно провести только одну прямую, перпендикулярную АВ, поэтому точки Р, О и N лежат на одной прямой. Значит, PN – диаметр окружности. Поскольку АРND – прямоугольник, то PN = AD, то есть

, что и требовалось доказать.

Теорема 3. Радиус описанной около квадрата окружности равен половине его диагонали:

$R=frac{sqrt{2}}{2}cdot a.$

Доказательство:

Диагонали квадрата АС и BD равны, пересекаются в точке О и делятся точкой пересечения пополам. Поэтому OA=OB=OC=OD, т.е. точки A, B, C и D лежат на одной окружности, радиус которой R = d/2 (d=AC=BD). Это и есть описанная около квадрата АВСD окружность.

По теореме

Тогда $R=afrac{sqrt{2}}{2}$ , что и требовалось доказать.

Заметим, что периметр квадрата тоже можно связать с радиусами вписанной и описанной окружностей:

Четырехугольник является квадратом, если выполняется хотя бы одно из условий:

Все стороны равны и среди внутренних углов есть прямой угол.
Диагонали равны, перпендикулярны и, пересекаясь, делятся пополам.

Разберем несколько простых задач на тему «Квадрат». Все они взяты из Банка заданий ФИПИ.

Задача 1. Найдите сторону квадрата, диагональ которого равна sqrt{8} .

Решение:

Мы знаем, что . Тогда $a=genfrac{}{}{}{0}{displaystyle d}{displaystyle sqrt{2}}= 2$ .

Ответ: 2.

Задача 2. Найдите площадь квадрата, если его диагональ равна 1.

Первый способ решения:

Зная связь между стороной и диагональю квадрата (теорема 1), выразим сторону квадрата через его диагональ:

$displaystyle d=sqrt{2}cdot a Rightarrow a=frac{d}{sqrt{2}}Rightarrow a=frac{1}{sqrt{2}}.$

Тогда по формуле площади квадрата:

$displaystyle S=a^{2}=left (frac{1}{sqrt{2}} right )^{2}=frac{1}{2}=0,5.$

Второй способ решения:

Воспользуемся формулой для площади ромба:

$displaystyle S=frac{1}{2}d_{1}d_{2}=frac{1}{2}d^{2}=0,5.$

Ответ: 0,5

Задача 3. Найдите радиус окружности, описанной около квадрата со стороной, равной sqrt{8} .

Решение:

Радиус описанной окружности равен половине диагонали квадрата, поэтому

$displaystyle R=frac{d}{2}=afrac{sqrt{2}}{2}=sqrt{8}cdot frac{sqrt{2}}{2}=2.$

Ответ: 2.

Задача 4. Найдите сторону квадрата, описанного около окружности радиуса .

Решение:

Диаметр окружности равен стороне квадрата: a=2r=8 .

Ответ: 8.

Задача 5. Радиус вписанной в квадрат окружности равен . Найдите диагональ этого квадрата.

Решение:

Сторона квадрата в два раза больше радиуса вписанной окружности:

Диагональ найдем, зная сторону квадрата:

Ответ: 56.

Задача 6. Радиус вписанной в квадрат окружности равен . Найдите радиус окружности, описанной около этого квадрата.

Решение:

Радиус окружности, вписанной в квадрат, равен половине стороны квадрата, а радиус описанной окружности равен половине диагонали квадрата:

$displaystyle r=frac{a}{2}; R=frac{d}{2}; d=asqrt{2}.$

Поэтому

Ответ: 22.

Задача 7. Найдите периметр квадрата, если его площадь равна 9.

Решение:

Найдем сторону квадрата:

Периметр квадрата со стороной 3 равен:

Ответ: 12.

Задача 8. Найдите площадь квадрата, в который вписан круг площадью 4pi .

Решение:

Площадь круга $S_{kp}=pi r^{2}=4pi ,$ откуда радиус круга равен 2.

Сторона квадрата в два раза больше радиуса вписанного круга и равна 4. Площадь квадрата равна 16.

Ответ: 16.

Задача 9. Найдите радиус окружности, вписанной в квадрат ABCD, считая стороны квадратных клеток равными sqrt{2} .

Решение:

Сторону квадрата найдем как диагональ другого квадрата со стороной 2 клеточки. Поскольку длина одной клеточки равна sqrt{2} ., то сторона малого квадрата равна . А сторона квадрата ABCD равна

Радиус вписанной окружности в два раза меньше стороны квадрата и равен 2.

Ответ: 2.

Задача 10. Найдите радиус r окружности, вписанной в четырехугольник ABCD. В ответе укажите .

Решение:

Считаем стороны клеток равными единице. Четырехугольник ABCD — квадрат. Все его стороны равны, все углы — прямые. Как и в предыдущей задаче, радиус окружности, вписанной в квадрат, равен половине его стороны.

Найдем на чертеже прямоугольный треугольник. По теореме Пифагора найдем сторону, например, AB.

Она равна . Тогда радиус вписанной окружности равен $genfrac{}{}{}{0}{displaystyle sqrt{10}}{displaystyle 2}$ . В ответ запишем .

Ответ: 5.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Квадратu0026nbsp;u0026mdash; определение иu0026nbsp;свойства» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Квадрат– прямоугольник, у которого все стороны равны. Квадрат является правильным четырёхугольником, у которого все углы равны и все стороны равны.
Квадрат — это частный случай четырехугольника, параллелограмма, прямоугольника и ромба, поэтому квадрат также обладает всеми их свойствами.

Свойства квадрата

Все стороны квадрата равны;
Все углы равны и составляют 90°;
Диагонали квадрата равны и перпендикулярны;
Диагонали квадрата являются биссектрисами углов.

Признаки квадрата

Если четырёхугольник является прямоугольником и ромбом, то он – квадрат.
Если у прямоугольника две смежные стороны равны, то он – квадрат.
Если диагональ прямоугольника является биссектрисой его углов, то он – квадрат.
Если у ромба есть прямой угол, то он – квадрат.
Если диагонали ромба равны, то он – квадрат.

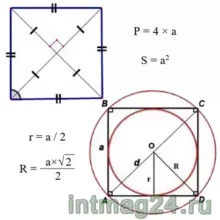
Основные формулы

Периметр:

Площадь по стороне квадрата. Площадь квадрата равна квадрату его стороны:

Площадь по диагоналям квадрата. Площадь квадрата равна половине произведения диагоналей:Сторона и диагональ связаны соотношениями:

где: P-периметр, S-площадь квадрата, a-сторона, d-диагональ.

Квадрат и окружность

Вокруг квадрата можно описать окружность.
В квадрат можно вписать окружность.

У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей.

Радиус описанной окружности:

Радиус вписанной окружности:

Калькулятор для квадрата поможет вычислить все характеристики квадрата (сторона, диагональ, периметр, площадь, радиус вписанной и описанной окружности) по одной из известных величин.

Источник