Как найти угол между биссектрисами смежных углов - Исправление недочетов и поиск решений вместе с Examum.ru

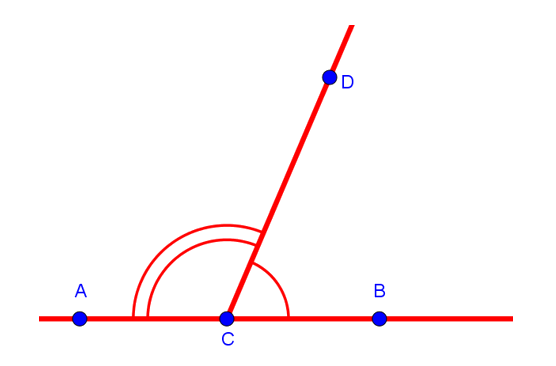
∠АОВ и ∠ВОС — смежные, и их сумма равна 180° (по свойству смежных углов).

Пусть OK — биссектриса ∠АОВ; OD — биссектриса ∠ВОС.

Выведем обозначения:

∠BOD = х, а ∠AOK = у. Тогда 2х + 2у = 180°, х + у = 90°. ∠KOD = х + у = 90°.

Ответ: 90°.

Источник

Зависит ли угол, который образуют между собой биссектрисы смежных углов, от градусных мер этих углов?

Утверждение.

Биссектрисы смежных углов перпендикулярны.

Дано: ∠AOD и ∠DOB — cмежные,

OF — биссектриса ∠AOD,

OK — биссектриса ∠DOB

Доказать:

Доказательство:

Так как сумма смежных углов равна 180º, то ∠AOD+∠DOB=180º.

Так как OF — биссектриса ∠AOD, то

$[angle FOD = frac{1}{2}angle AOD.]$

Так как OK — биссектриса ∠DOB, то

$[angle DOK = frac{1}{2}angle DOB.]$

Отсюда,

$[angle FOD + angle DOK = frac{1}{2}angle AOD + frac{1}{2}angle DOB = ]$

$[ = frac{1}{2}(angle AOD + angle DOB) = frac{1}{2} cdot {180^o} = {90^o}.]$

Таким образом, мы доказали, что угол между биссектрисами смежных углов не зависит от градусной меры смежных углов и всегда равен 90º, то есть, биссектрисы смежных углов перпендикулярны.

Задача.

Найти угол между биссектрисами смежных углов, один из которых на 100º больше другого.

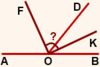
Решение:

Так как биссектрисы смежных углов перпендикулярны, ∠FOK=90º.

(Находить градусные меры смежных углов не требуется).

Ответ: 90º.

Источник

Введение

В этом году мы начали изучать новый предмет – геометрию. Все время, когда мы имеем дело с формой, размером, положением предмета в пространстве, мы вовлечены в геометрию. Когда доисторические люди занимались ткачеством или отделкой зданий, они пользовались геометрией, не зная ее. Древним египтянам была нужна геометрия, чтобы измерить участки земли, подвергавшиеся затоплению во время разливов Нила. Им была нужна геометрия в строительных целях, когда религия заставила их строить могилы для умерших — пирамиды. Само слово «геометрия» произошло от греческих слов «Земля» и «измерять» и, вероятно, является переводом египетского слова.

Сначала геометрия была интуитивной. Это означает, что факты признавались существующими без попытки доказать это или продемонстрировать, что это действительно так. Но в 600 году до н.э. греческий ученый Фалес развил идею, что должны существовать пути, доказывающие, что геометрические факты истинны. В геометрии такая истина называется теоремой. Фалес открыл доказательства теорем, которые люди принимали на веру до этого времени. Это послужило началом доказательной геометрии.

В результате люди накапливали знания, опыт, формулировались правила, связанные с геометрическими измерениями и построениями, потом выдвигались гипотезы, формулировались и доказывались теоремы.

Меня очень заинтересовала геометрия и мне захотелось самой решить практическую задачу по геометрии и на ее основе выдвинуть и доказать гипотезу. Моя работа построена по следующей схеме:

Задача.

Найти угол между биссектрисами двух смежных углов.

Постановка проблемы.

Зависит ли значение угла между биссектрисами двух смежных углов от выбора угла и его значения?

Разбор частных случаев.

Берется несколько частных случаев значений одного из смежных углов и вычисляется угол между биссектрисами. Рассматриваются случаи:

Оформление результатов исследования.

Полученные результаты исследования оформляются в виде таблицы.

Выдвижение гипотезы.

Возникает гипотеза о том, что угол между биссектрисами двух смежных углов равен .

Доказательство или проверка гипотезы.

Доказательство данной гипотезы.

Применение результатов исследования.

Задачи, в которых может применяться данное утверждение.

Глава 1

Задача

Найти угол между биссектрисами двух смежных углов.

Постановка проблемы

Зависит ли значение угла между биссектрисами двух смежных углов от выбора угла и его значения?

Разбор частных случаев

а)

Пусть =140о, тогда смежный с ним угол равен 40о. Поэтому угол между биссектрисами равен: 20о + 70о = 90о

б)

Пусть =70о, а смежный с ним угол равен 110о. Поэтому угол между биссектрисами равен: 35о +55о = 90о

в)

Пусть и смежный с ним угол равен 90о. Поэтому угол между биссектрисами равен: 45о + 45о = 90о

г)

Пусть =41о, а смежный с ним угол равен 139о. Поэтому угол между биссектрисами равен: 20,5о + 69,5о = 90о

Оформление результатов исследования

Полученные результаты отобразим в таблице.

	Угол между биссектрисами двух смежных углов
а) =140о	90о
б) =70о	90о
в) =90о	90о
с) =41о	90о

Выдвижение гипотезы

У меня получилось, что во всех случаях угол между биссектрисами равен 90о. Значит можно выдвинуть гипотезу – угол между биссектрисами двух смежных углов равен 90о.

Доказательство или проверка гипотезы

Обозначим один из смежных углов , тогда другой угол – 180°–.

1=, так как биссектриса делит угол пополам

2= .

Нам надо найти угол между биссектрисами, значит

+ = – + 90° = 90°.

В общем случае я получила, что угол между биссектрисами равен 90о, также как и в частных случаях. Следовательно, угол между биссектрисами 2-х смежных углов действительно равен 90°.

Применение результатов исследования

Результаты данной работы могут найти применение в задачах различного вида. Например, такой:

На биссектрисах двух смежных углов взяты произвольные точки А и В.

Решение

Т.к. треугольник АВС – прямоугольный, то больший угол = 90°( по теореме о сумме углов треугольника), а против большего угла лежит большая сторона, т.е. АВ — большая сторона треугольника АВС.

САВ + АВС= 90°( по теореме о сумме углов треугольника).

ВС=1/2 АВ=1/2с, т.к. в прямоугольном треугольнике против угла 30° лежит катет, равный половине гипотенузы. Отсюда же и АВ= 2.

Т.к. длина перпендикуляра, проведенного из точки к прямой, называется расстоянием от этой точки до прямой, то в данном случае расстояние от точки В до прямой АС будет равно ВС, а расстояние от точки А до прямой ВС будет равно АС.

Заключение

В ходе исследования данной задачи я убедилась в том, угол между биссектрисами любых смежных углов равен 90°.

На основе полученных данных мы можем решать задачи, используя свойства прямоугольного треугольника, построенного на биссектрисах смежных углов:

Сумма острых углов прямоугольного треугольника равна 90°.
Катет прямоугольного треугольника, лежащий против угла 30°,

равен половине гипотенузы.

Если катет прямоугольного треугольника равен половине

гипотенузы, то угол, лежащий против этого катета, равен 30°.

А также различные задачи, где используются другие свойства прямоугольного треугольника.

Список литературы

Геометрия, 7-9:учеб. для общеобразоват.учреждений/Л.С. Атанасян, В.Ф.Бутузов и др.
Энциклопедия для школьников. Математика. Гл.ред. М. Аксенова. Изд. «Аванта»

Источник

Допустим углы А и В — смежные и, соответственно, в сумме образуют развернутый угол в 180 градусов.

Биссектрисы делят оба угла пополам, а значит угол между этими биссектрисами будет равен сумме половин этих двух углов Х = А/2 + В/2, где Х — размер угла, образованного биссектрисами.

Упростим полученное выражение: Х = А/2 + В/2 = ( А + В )/2

Так как смежные углы в сумме образуют развернутый угол в 180 градусов, то

( А + В )/2 = 180/2 = 90

Из этого следует, что угол, образованный биссектрисами смежных углов, — прямой и равен 90 градусов или, как можно сказать другими словами, биссектрисы смежных углов перпендикулярны друг другу.

Источник

В данной статье репетитор по математике и физике отвечает на вопрос, чему равен угол между биссектрисами смежных углов. Как оказалось, этот вопрос волнует многих школьников, которым предстоит сдавать ЕГЭ или ОГЭ по математике. Интересно то, что этот материал изучается в 7 классе, когда школьники только начинают своё знакомство с премудростями геометрии. Дочитайте эту статью до конца, и вы не только узнаете чему равен угол между биссектрисами смежных углов, но и поймёте, как это можно очень легко доказать.

Чему равен угол между биссектрисами смежных углов

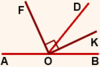
Начать нужно, конечно, с определения смежных углов. Смежными называются углы, которые как бы дополняют друг друга до развёрнутого. Проще всего продемонстрировать это с помощью рисунка. Если нарисовать прямую AB, отметить на ней между точками A и B точку C и провести из неё луч CD, то углы ACD и DCB будут являться смежными. На рисунке они отмечены одной и двумя дугами:

Ну и понятно, что поскольку смежные углы дополняют друг друга до развёрнутого угла, то в сумме они равны $180^{circ}$ .

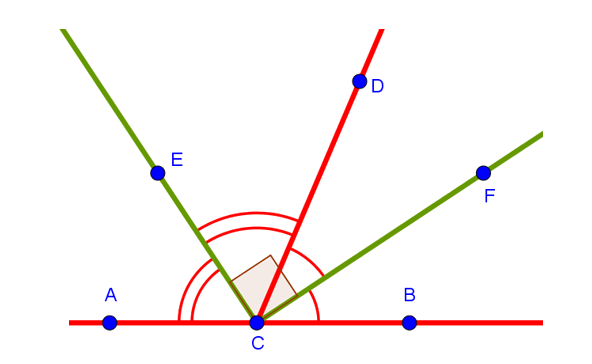
Проведём теперь биссектрисы этих смежных углов. Напомню, что биссектрисой называется «крыса, которая бегает по углам и делит угол пополам». Это такая запоминалочка для семиклассников, чтобы лучше запомнить. А если более строго, так сказать, по-научному, то биссектриса — это луч, исходящий из вершины угла и делящий его пополам. Ну и если нарисовать биссектрисы обоих углов (на рисунке снизу это зелёные линии CE и CF), то даже визуально заметно, что угол между ними составит $90^{circ}$ :

Кто-то может мне возразить, сказав, что это случайно так получилось и что можно перерисовать рисунок так, что биссектрисы уже не будут взаимно перпендикулярны. Но нет! В том то и дело, что можно взять какие угодно смежные углы и угол между биссектрисами этих смежных углов обязательно будет прямым. Это удивительный факт, не правда ли?!

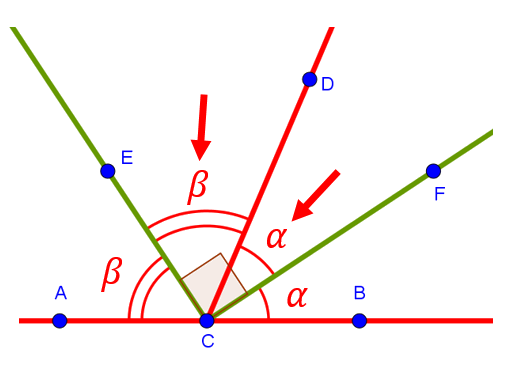
Но на самом деле, если вы уже были с ним раньше знакомы, то не на столько уж удивительный. Потому что на самом деле доказательство у этого факта довольно-таки простое. Обозначим равные углы FCB и DCF за , а равные углы DCE и ECA за :

Если посмотреть на рисунок, то все эти углы вместе образуют развёрнутый угол, то есть в сумме все они равны $180^{circ}$ . То есть имеет место равенство:

$[ 2alpha + 2beta = 180^{circ}. ]$

Если разделить обе части этого равенства на 2, то получится:

$[ alpha + beta = 90^{circ}. ]$

То есть два уголочка в центре дают в сумме $90^{circ}$ вне зависимости от величины каждого из этих углов. То есть угол ECF — прямой. Что и требовалось доказать.

Вот такой замечательный факт из элементарной геометрии. И таких фактов очень много. На своих занятиях я рассказываю о них своим ученикам. Помимо того, что это просто интересно, это ещё и очень пригодится в будущем при сдаче различных экзаменов по математике, в первую очередь ОГЭ и ЕГЭ.

Материал подготовил репетитор по математике, Сергей Валерьевич

Источник