Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма
Параллелограмм — это четырехугольник, имеющий две пары параллельных сторон.
Свойства параллелограмма:
- Противоположные стороны параллелограмма равны.
- Противоположные углы параллелограмма равны.
- Диагонали параллелограмма в точке пересечения делятся пополам.
Давайте посмотрим, как свойства параллелограмма применяются в решении задач ЕГЭ.
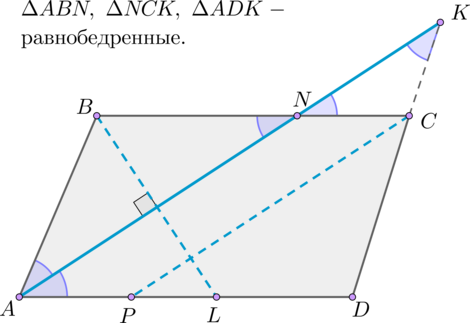
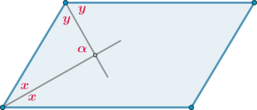
1. Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Пусть и
— биссектрисы углов параллелограмма, прилежащих к стороне
. Сумма углов
и
равна
. Углы
и
— половинки углов
и
. Значит, сумма углов
и
равна
градусов. Из треугольника
находим, что угол
— прямой.
Ответ: .
Биссектрисы углов параллелограмма, прилежащих к одной стороне, — перпендикулярны.
Легко доказывается и другое свойство биссектрис параллелограмма:
Биссектрисы противоположных углов параллелограмма — параллельны.
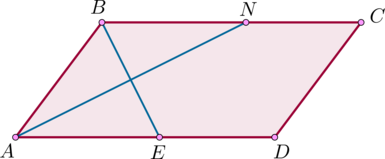
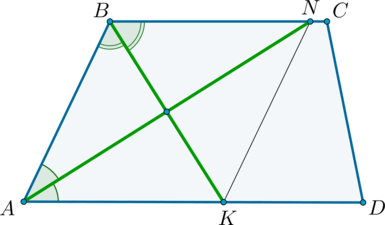
2. Точка пересечения биссектрис двух углов параллелограмма, прилежащих к одной стороне, принадлежит противоположной стороне. Меньшая сторона параллелограмма равна . Найдите его большую сторону.
Найдем на этом рисунке накрест лежащие углы. Мы уже рассказывали, что это такое.
Углы и
, а также
и
— накрест лежащие. Накрест лежащие углы равны. Значит, угол
равен углу
, а угол
— углу
.
Получаем, что треугольники и
— равнобедренные, то есть
, а
.
Тогда .
Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Запишем формулы площади параллелограмма:
, где
— основание параллелограмма,
— его высота.
, где
и
— стороны параллелограмма,
— угол между ними.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Параллелограмм иu0026nbsp;его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Найдите угол между биссектрисами углов параллелограмма
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Решение:
Параллелограмм и его свойства. Площадь параллелограмма. Биссектрисы углов параллелограмма
Параллелограмм —
это четырехугольник, имеющий две пары
параллельных сторон.
Свойства
параллелограмма:
-
Противоположные стороны параллелограмма
равны. -
Противоположные
углы параллелограмма равны. -
Диагонали
параллелограмма в точке пересечения
делятся пополам.
Давайте
посмотрим, как свойства параллелограмма
применяются в решении задач ЕГЭ.
1.
Найдите угол между биссектрисами углов
параллелограмма, прилежащих к одной
стороне. Ответ дайте в градусах.
Пусть
ВМ и СК — биссектрисы углов
параллелограмма, прилежащих к стороне
ВС. Сумма углов АВС и BCD равна 180°. Углы
ОВС и ОСВ — половинки углов АВС
и ВСD. Значит, сумма углов АВС и ВСD
равна 90 градусов. Из треугольника
ВОС находим, что угол ВОС — прямой.
Ответ: 90.
Биссектрисы
углов параллелограмма, прилежащих
к одной стороне, — перпендикулярны.
Легко
доказывается и другое свойство
биссектрис параллелограмма:
Биссектрисы
противоположных углов параллелограмма —
параллельны.
2.
Точка пересечения биссектрис двух углов
параллелограмма, прилежащих к одной
стороне, принадлежит противоположной
стороне. Меньшая сторона параллелограмма
равна 5. Найдите его большую сторону.
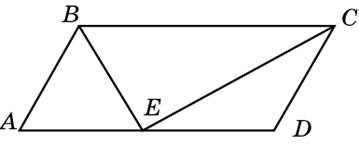
Найдем
на этом рисунке накрест лежащие углы.
Мы уже рассказывали, что это такое.
Углы
СВЕ и ВЕА, а также СЕD и ВСЕ —
накрест лежащие. Накрест лежащие углы
равны. Значит, угол СВЕ равен углу ВЕА,
а угол СЕD — углу ВСЕ.
Получаем,
что треугольники АВС и CDE —
равнобедренные, то есть АЕ = АВ, а DЕ
= CD. Тогда AD = 5 + 5 = 10.
Биссектриса
угла параллелограмма отсекает от него
равнобедренный треугольник.
Запишем
формулы
площади параллелограмма:
S
= ah, где а — основание параллелограмма,
h — его высота.
S = ab sin φ, где
а и b — стороны параллелограмма,
φ — угол между ними.
И еще
одна формула. Так же, как и свойства
биссектрис углов параллелограмма, эта
формула пригодится тем, кто нацелен
на решение задачи С4.
S
=
d1 d2 sin α,
где d1 и d2 — диагонали
параллелограмма, α — угол между ними.
Прямоугольник
и его свойства
Прямоугольник —
это параллелограмм, у которого все
углы прямые.
Диагонали
прямоугольника равны.
1.
В прямоугольнике диагональ делит
угол в отношении 1:2, меньшая его
сторона равна 6. Найдите диагональ
данного прямоугольника.
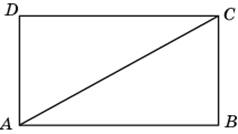
Всё
просто. Рассмотрите прямоугольный
треугольник АВС. Найдите, чему равен
угол САВ и его синус, а затем найдите
АС.
Ответ:
12.
А сейчас
рассмотрим еще одну задачу, в которой
применяются свойства диагоналей
прямоугольника.
2.
Острые углы прямоугольного треугольника
равны 24° и 66°. Найдите угол между
высотой и медианой, проведенными
из вершины прямого угла. Ответ дайте
в градусах.
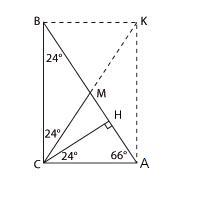
Казалось бы,
при чем здесь прямоугольник? Дан
прямоугольный треугольник, из вершины
прямого угла проведены высота и медиана.
А что можно сказать о длине этой
медианы?
Давайте
достроим чертеж до прямоугольника.
Поскольку диагонали прямоугольника
равны (это свойство прямоугольника)
и делятся пополам в точке пересечения,
отрезки СМ, ВМ и АМ тоже будут
равны. Каждый из них равен половине
диагонали прямоугольника. Мы доказали
теорему:
В прямоугольном
треугольнике медиана, проведенная
к гипотенузе, равна половине гипотенузы.
Итак,
ВМ = СМ, значит, треугольник ВМС
равнобедренный, и угол ВСМ равен 24°.
По свойству
высоты, проведенной из вершины прямого
угла,
∠АСН
= ∠АВС
= 24°.
Тогда
угол МСН (между медианой и высотой
треугольника АВС) равен 90° — 24° —
24° = 42°.
Ответ: 42.
Как
вы думаете, где находится центр
окружности, описанной вокруг прямоугольного
треугольника? Ведь центр описанной
окружности — точка, равноудаленная
от всех вершин треугольника. Очевидно,
эта точка — середина гипотенузы.
В прямоугольном
треугольнике центром описанной окружности
является середина гипотенузы.
1.
Найдите диагональ прямоугольника,
вписанного в окружность, радиус
которой равен 5.
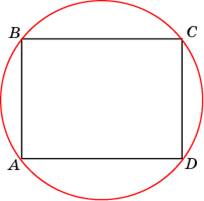
Проведем
диагональ АС. Получим, что АС равна
2R.
Ответ: 10.
Ромб
и его свойства
По определению,
ромб — это параллелограмм, все стороны
которого равны.
Свойства
ромба:
-
Диагонали
ромба перпендикулярны. -
Диагонали
ромба делят его углы пополам.
Воспользуемся
свойствами ромба для решения задач.
1.
Найдите меньшую диагональ ромба, стороны
которого равны 2, а острый угол
равен 60°.
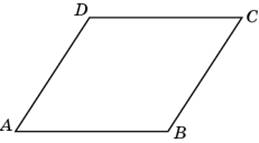
Проведите
меньшую диагональ ромба и рассмотрите
треугольник ADB. Поскольку AD = DB, а угол
DAB равен 60°, треугольник ADB —
равносторонний. Следовательно, меньшая
диагональ ромба равна 2.
1.
Найдите высоту ромба, сторона которого
равна v3, а острый угол равен 60?.
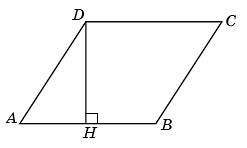
Один
из подходов к решению задач
по геометрии — метод площадей.
Он состоит в том, что площадь фигуры
выражается двумя разными способами,
а затем из полученного уравнения
находится неизвестная величина.
Пусть
а — сторона ромба. Тогда
S
= a2
sin 60° = ah,
Отсюда
.
2.
Диагонали ромба относятся как 3:4. Периметр
ромба равен 200. Найдите высоту ромба.
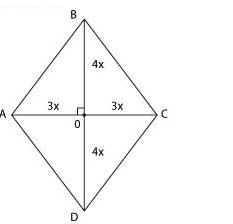
Пусть
диагонали ромба равны 6х и 8х.
Диагонали ромба перпендикулярны,
значит, треугольник АОВ — прямоугольный.
По теореме Пифагора АВ2
= АО2
+ ОВ2
АВ2
= 9×2
+ 16×2,
АВ2
= 25×2,
Отсюда АВ = 5х.
Поскольку периметр
равен 200,
5х · 4 = 200
х = 10, АВ = 50,
а диагонали ромба равны 60 и 80.
Нам
надо найти высоту ромба.
Давайте
запишем, чему равна площадь ромба.
С одной стороны, S = ah. С другой
стороны, площадь ромба складывается
из площадей двух равных треугольников
АВС и ADC, то есть равна 60 · 40 = 2400.
Отсюда h = S : a = 2400 : 50 = 48.
Ответ:
48.
Квадрат —
определение и свойства
Квадрат —
это прямоугольник, у которого все
стороны равны.
Можно дать и другое определение
квадрата:
квадрат —
это ромб, у которого все углы прямые.
Получается,
что квадрат обладает всеми свойствами
параллелограмма, прямоугольника и ромба.
Перечислим
свойства
квадрата:
-
Все
углы квадрата — прямые, все стороны
квадрата — равны. -
Диагонали
квадрата равны и пересекаются под
прямым углом. -
Диагонали
квадрата делят его углы пополам.
Площадь
квадрата, очевидно, равна квадрату его
стороны: S = a2.
Диагональ квадрата равна произведению
его стороны на
,
то есть
,
Разберем
несколько простых задач на тему
«Квадрат». Все они взяты из Банка
заданий ФИПИ.
1.
Найдите сторону квадрата, диагональ
которого равна
.
Мы знаем,
что
.
Тогда
.
2.
Найдите радиус окружности, описанной
около квадрата со стороной, равной
.

Очевидно,
радиус окружности равен диагонали
квадрата.
Ответ:
4.
3.
Найдите сторону квадрата, описанного
около окружности радиуса 4.

Диаметр
окружности равен стороне квадрата.
Ответ:
8.
4.
Найдите радиус окружности, вписанной
в квадрат ABCD, считая стороны квадратных
клеток равными
.
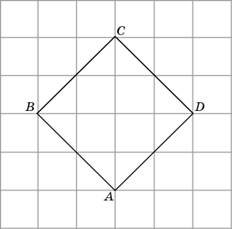
Чуть
более сложная задача. Нарисуйте
окружность, вписанную в данный
квадрат, то есть касающуюся всех его
сторон. Вы увидите, что диаметр этой
окружности равен стороне квадрата.
Ответ:
2.
5.
Найдите радиус r окружности, вписанной
в четырехугольник ABCD. В ответе
укажите
.
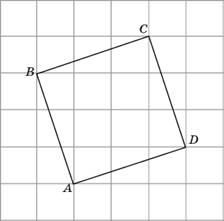
Считаем
стороны клеток равными единице.
Четырехугольник ABCD — квадрат. Все
его стороны равны, все углы — прямые.
Как и в предыдущей задаче, радиус
окружности, вписанной в квадрат,
равен половине его стороны.
Найдем
на чертеже прямоугольный треугольник.
По теореме Пифагора найдем сторону,
например, АВ. Она равна
.
Тогда радиус вписанной окружности равен
.
В ответ запишем
.
Ответ:
5.
Трапеция
и ее свойства
Трапеция —
четырехугольник, у которого две
стороны параллельны, а две другие —
нет.
Параллельные
стороны трапеции называются основаниями.
Другие две — боковые стороны.
Если
боковые стороны равны, трапеция называется
равнобедренной.
Площадь
трапеции равна произведению полусуммы
оснований на высоту:
Отрезок,
соединяющий середины оснований трапеции,
называется средней линией трапеции.
Средняя линия трапеции параллельна
основаниям, а длина ее равна
полусумме оснований:
Как
видим, теория очень проста. А задачи,
в которых применяются свойства
трапеции, весьма разнообразны. В этой
статье разобраны и стандартные задачи
(номер 1 и 2), и более интересные.
1.
Найдите высоту трапеции ABCD, опущенную
из вершины B, если стороны квадратных
клеток равны
.
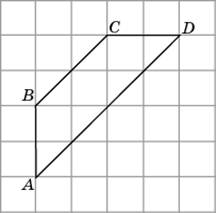
Высота
трапеции — это отрезок, перпендикулярный
ее основаниям. Проведем высоту
из вершины В.
Ответ:
2.
2.
Основания трапеции равны 18 и 6,
боковая сторона, равная 7, образует
с одним из оснований трапеции угол
150. Найдите площадь трапеции.
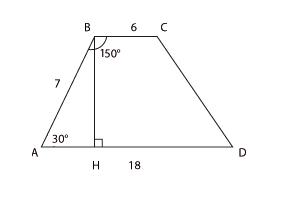
Это
стандартная задача. Углы АВН и ВАН —
односторонние, значит, их сумма равна
180°, и тогда угол ВАН равен 30°.
Из треугольника АВН найдем высоту
ВН. Катет, лежащий напротив угла в 30,
равен половине гипотенузы. Получаем,
что ВН = 3,5 и площадь трапеции
равна 42.
3.
Основания трапеции равны 4 и 10.
Найдите больший из отрезков, на которые
делит среднюю линию этой трапеции одна
из ее диагоналей.
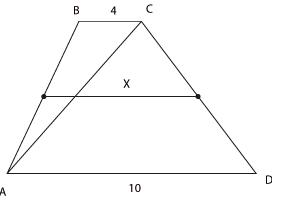
Скажите,
что вы видите на чертеже? Можно
сказать, что изображена трапеция АВСD,
и в ней проведена средняя линия.
А можно увидеть и другое — два
треугольника, АВС и АСD, в которых
проведены средние линии.
Мы помним,
что средняя линия треугольника —
это отрезок, соединяющий середины двух
его сторон. Средняя линия треугольника
параллельна третьей его стороне и равна
половине этой стороны.
Из треугольника
АВD находим: х = 5.
В следующей
задаче мы тоже воспользуемся свойством
средней линии треугольника.
4.
Основания трапеции равны 3 и 2.
Найдите отрезок, соединяющий середины
диагоналей трапеции.
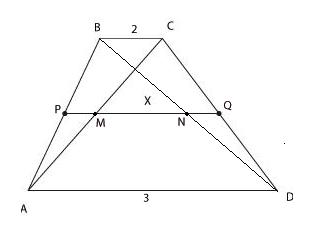
Проведем
PQ — среднюю линию трапеции, PQ = 2,5.
Легко доказать, что отрезок MN,
соединяющий середины диагоналей
трапеции, лежит на средней линии.
Дальше все просто. Найдем отрезки РМ
и NQ, являющиеся средними линиями
треугольников ABC и BCD, а затем
отрезок MN. Он равен 0,5.
5.
Прямая, проведенная параллельно боковой
стороне трапеции через конец меньшего
основания, равного 4, отсекает
треугольник, периметр которого равен
15. Найдите периметр трапеции.
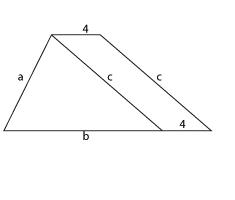
Периметр
треугольника равен сумме его сторон,
то есть a + b + c.
Периметр трапеции
равен а + b + 4 + c + 4.
На сколько
периметр трапеции больше периметра
треугольника? Чему равен периметр
трапеции?
Ответ:
23.
Окружность.
Центральный и вписанный угол
Центральный
угол —
это угол, вершина которого находится
в центре окружности.
Вписанный
угол —
угол, вершина которого лежит на окружности,
а стороны пересекают ее.
На рисунке —
центральные и вписанные углы, а также
их важнейшие свойства.
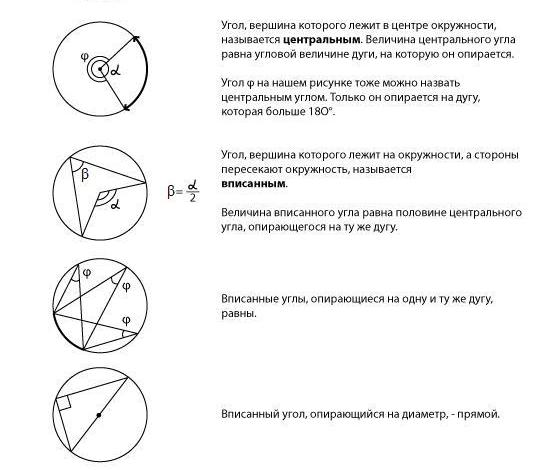
Итак,
величина
центрального угла равна угловой величине
дуги, на которую он опирается.
Значит,
центральный угол величиной в 90 градусов
будет опираться на дугу, равную 90°,
то есть
круга.
Центральный угол, равный 60°, опирается
на дугу в 60 градусов, то есть
на шестую часть круга.
Величина
вписанного угла в два раза меньше
центрального, опирающегося на ту же
дугу.
Также
для решения задач нам понадобится
понятие «хорда».

Равные
центральные углы опираются на равные
хорды.
1.
Чему равен вписанный угол, опирающийся
на диаметр окружности? Ответ дайте
в градусах.
Вписанный
угол, опирающийся на диаметр, —
прямой.
Ответ:
90.
2.
Центральный угол на 36° больше
острого вписанного угла, опирающегося
на ту же дугу окружности. Найдите
вписанный угол. Ответ дайте в градусах.
Пусть
центральный угол равен х, а вписанный
угол, опирающийся на ту же дугу,
равен у.
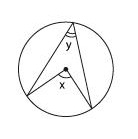
Мы знаем,
что х = 2у.
Отсюда 2у = 36 + у,
у = 36.
Ответ:
36.
3.
Радиус окружности равен 1. Найдите
величину тупого вписанного угла,
опирающегося на хорду, равную
.
Ответ дайте в градусах.
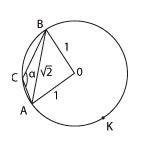
Пусть
хорда АВ равна
.
Тупой вписанный угол, опирающийся на эту
хорду, обозначим ?.
В треугольнике
АОВ стороны АО и ОВ равны 1,
сторона АВ равна
.
Нам уже встречались такие треугольники.
Очевидно, что треугольник АОВ —
прямоугольный и равнобедренный,
то есть угол АОВ равен 90°.
Тогда
дуга АСВ равна 90°, а дуга АКВ равна
360° — 90° = 270°.
Вписанный угол
? опирается на дугу АКВ и равен
половине угловой величины этой дуги,
то есть 135°.
Ответ:
135.
4.
Хорда AB делит окружность на две
части, градусные величины которых
относятся как 5:7. Под каким углом видна
эта хорда из точки C, принадлежащей
меньшей дуге окружности? Ответ дайте
в градусах.
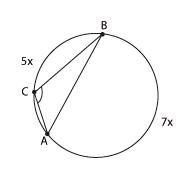
Главное
в этой задаче — правильный чертеж
и понимание условия. Как вы понимаете
вопрос: «Под каким углом хорда видна
из точки С?»
Представьте, что
вы сидите в точке С и вам
необходимо видеть всё, что происходит
на хорде АВ. Так, как будто хорда АВ —
это экран в кинотеатре 
Очевидно,
что найти нужно угол АСВ.
Сумма двух
дуг, на которые хорда АВ делит
окружность, равна 360°, то есть
5х +
7х = 360°
Отсюда х = 30°, и тогда вписанный
угол АСВ опирается на дугу, равную
210°.
Величина вписанного угла равна
половине угловой величины дуги, на которую
он опирается, значит, угол АСВ равен
105°.
Ответ:
105.
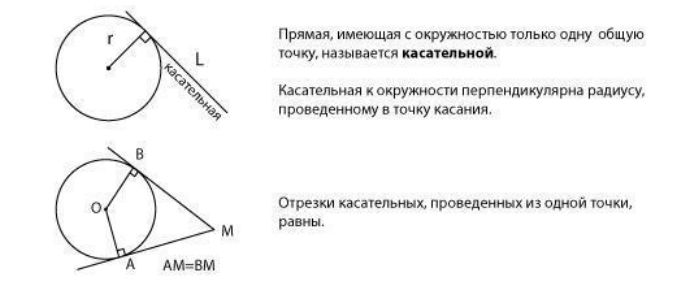
Касательная
к окружности
Касательная
к окружности — прямая, имеющая
с окружностью единственную общую
точку.
Понятие
касательной к окружности и основные
свойства касательной проиллюстрированы
ниже на рисунке.
1.
Угол ACO равен 28°, где O — центр
окружности. Его сторона CA касается
окружности. Найдите величину меньшей
дуги AB окружности, заключенной внутри
этого угла. Ответ дайте в градусах.
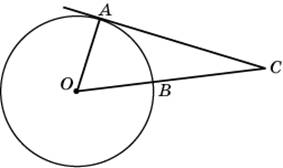
Касательная
к окружности перпендикулярна радиусу,
проведенному в точку касания. Значит,
угол САО — прямой. Из треугольника
АСО получим, что угол АОС равен 62 градуса.
Величина центрального угла равна угловой
величине дуги, на которую он опирается,
значит, величина дуги АВ — тоже
62 градуса.
Ответ:
62.
2.
Найдите угол ACO, если его сторона CA
касается окружности, O — центр
окружности, а большая дуга AD
окружности, заключенная внутри этого
угла, равна 116°. Ответ дайте в градусах.
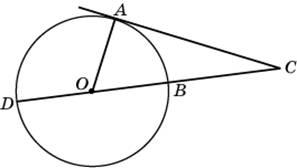
Это
чуть более сложная задача. Центральный
угол АОD опирается на дугу AD,
следовательно, он равен 116 градусов.
Тогда угол АОС равен 180° — 116° = 64°.
Касательная перпендикулярна радиусу,
проведенному в точку касания, значит,
угол ОАС — прямой. Тогда угол АСО
равен 90° — 64° = 26°.
Ответ:
26.
3.
Хорда AB стягивает дугу окружности
в 92°. Найдите угол ABC между этой хордой
и касательной к окружности,
проведенной через точку B. Ответ дайте
в градусах.
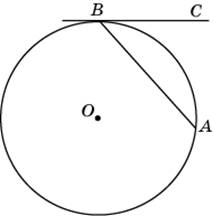
Проведем
радиус ОВ в точку касания, а также
радиус ОА. Угол ОВС равен 90°. Треугольник
ВОА — равнобедренный. Нетрудно найти,
что угол ОВА равен 44 градуса, и тогда
угол СВА равен 46 градусов, то есть
половине
угловой величины дуги АВ.
Получается,
что
угол между касательной и хордой,
проведенной через точку касания, равен
половине угловой величины дуги,
заключенной между ними.
4.
Через концы A, B дуги окружности
в 62° проведены касательные AC
и BC. Найдите угол ACB. Ответ дайте
в градусах.
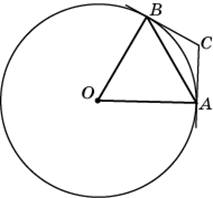
Рассмотрите
четырехугольник ОВСА. Сумма углов любого
выпуклого четырехугольника равна 360°.
Углы ОВА и ОВС и ОАС — прямые,
угол ВОА равен 62°, значит, угол АСВ
равен 28 градусов.
Ответ:
28.
5.
К окружности, вписанной в треугольник
ABC, проведены три касательные. Периметры
отсеченных треугольников равны 6, 8, 10.
Найдите периметр данного треугольника.
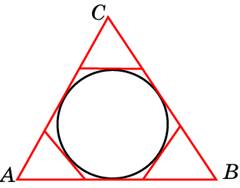
Вспомним
еще одно важное свойство касательных
к окружности:
Отрезки
касательных, проведенных из одной
точки, равны.
Периметр треугольника — это сумма
всех его сторон. Обратите внимание
на точки на нашем чертеже, являющиеся
вершинами шестиугольника. Из каждой
такой точки проведены два отрезка
касательных к окружности. Отметьте
на чертеже такие равные отрезки. Еще
лучше, если одинаковые отрезки вы будете
отмечать одним цветом. Постарайтесь
увидеть, как периметр треугольника АВС
складывается из периметров отсеченных
треугольников.
Ответ:
24.
Все
эти задачи встречаются в Банке заданий
ФИПИ под номером В6. А вот одна
из сложных задач В3:
6.
Около окружности описан многоугольник,
площадь которого равна 5. Его периметр
равен 10. Найдите радиус этой окружности.
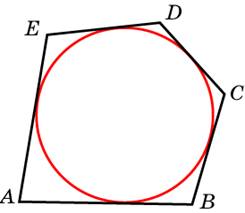
Обратите
внимание — в условии даже не сказано,
сколько сторон у этого многоугольника.
Видимо, это неважно. Пусть их будет
пять, как на рисунке.
Окружность
касается всех сторон многоугольника.
Отметьте центр окружности — точку
О — и проведите перпендикулярные
сторонам радиусы в точки касания.
Соедините
точку О с вершинами А, В, С, D, E.
Получились треугольники АОВ, ВОС, СОD,
DOE и ЕОА.
Очевидно, что площадь
многоугольника S = SАОВ
+ SВОС
+ SСОD
+ SDOE
+ SЕОА.
Как вы думаете, чему равны высоты
всех этих треугольников и как,
пользуясь этим, найти радиус окружности?
Ответ:
1.
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Биссектриса параллелограмма — это отрезок, соединяющий вершину параллелограмма с точкой на одной из двух противоположных сторон и делящий угол при вершине пополам.
(bullet) Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
(bullet) Биссектрисы соседних углов параллелограмма взаимно перпендикулярны: (BLperp AN).
(bullet) Биссектрисы противоположных углов параллелограмма параллельны: (ANparallel CP).
Задание
8
#1689
Уровень задания: Равен ЕГЭ
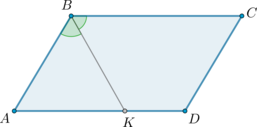
В параллелограмме (ABCD): (BK) – биссектриса, (BK = AK). Чему равен (angle D)?
Т.к. биссектриса отсекает равнобедренный треугольник от параллелограмма, то (AK = AB). Значит (triangle ABC) равносторонний (Rightarrow) (angle A = 60^circ) (Rightarrow) (angle D = 180^circ — 60^circ = 120^circ).
Ответ: 120
Задание
9
#3085
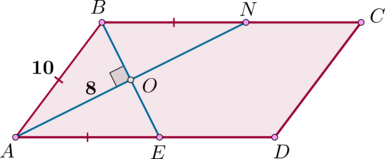
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD) проведены биссектрисы (AN) и (BE) односторонних углов. Найдите (BE), если (AN=16), (AB=10).
По свойству биссектрисы параллелограмма (triangle ABE) и (triangle
ABN) – равнобедренные, то есть (AE=AB=BN). Следовательно, (AO) – биссектриса, проведенная к основанию, значит, высота, то есть (angle AOB=90^circ), а также и медиана, то есть (BO=OE). Аналогично (AO=ON=frac12AN=8). Тогда по теореме Пифагора из (triangle AOB): [BO=sqrt{AB^2-AO^2}=6 quadRightarrowquad BE=2cdot 6=12.]
Ответ: 12
Задание
10
#279
Уровень задания: Равен ЕГЭ
В параллелограмме (ABCD): (BC = 2cdot AB), (AN) и (CM) – биссектрисы, (AB = 4). Найдите (NM).
Внутренние накрест лежащие углы при параллельных прямых и секущей равны, тогда (angle BNA = angle NAD), но (angle NAD = angle BAN), тогда (angle BNA = angle BAN) и треугольник (BAN) – равнобедренный, (AB = BN). Обозначим (AB = x).
Аналогично треугольник (MCD) – равнобедренный, (x = CD = MD).
(BC = 2x = AD), тогда (NC = x = AM), следовательно, (BN = x = AM); (AM parallel BN), тогда (ABNM) – параллелограмм, откуда заключаем, что (MN = AB = 4).
Ответ: 4
Задание
11
#1692
Уровень задания: Сложнее ЕГЭ
В параллелограмме (ABCD) биссектрисы (BK) и (AL) пересекаются в точке (O). Найдите периметр параллелограмма (ABCD), если (AD = 10), а медиана (OM) в (triangle AOB) равна (4).
(angle AOB = 90^circ) (Rightarrow) (OM = frac{1}{2}cdot AB), т.к. в прямоугольном треугольнике медиана, проведенная из прямого угла, равна половине гипотенузы. Тогда (AB = 2cdot 4 = 
Ответ: 36
Задание
12
#2951
Уровень задания: Сложнее ЕГЭ
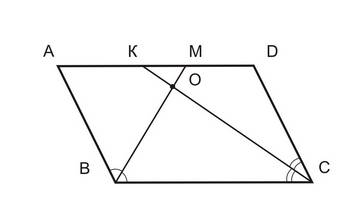
В трапеции (ABCD) с основаниями (AD) и (BC) проведены биссектрисы углов (A) и (B), пересекающие основания соответственно в точках (N) и (K). Найдите периметр четырехугольника (ABNK), если (AB=5).
(Задача от подписчиков)
(angle AKB=angle KBN) как накрест лежащие при (ADparallel BC) и (BK) секущей. Следовательно, (angle AKB=angle ABK), следовательно, (triangle BAK) равнобедренный. Отсюда (AB=AK=5).
Аналогично, (angle BNA=angle NAK=angle NAB), следовательно, (triangle ABN) – равнобедренный. Отсюда (AB=BN=5).
Заметим, что (AK=BN=5) и (AKparallel BN), следовательно, по признаку (ABNK) – параллелограмм. Следовательно, (NK=AB=5). Следовательно, периметр (ABNK) равен (5+5+5+5=20).
Ответ: 20
Задание
13
#3678
Уровень задания: Равен ЕГЭ
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Проведем биссектрисы двух соседних углов. Пусть они разбили первый угол на два угла, равных (x), второй угол — на два угла, равных (y). Нужно найти (alpha).
По свойству параллелограмма сумма его углов, прилежащих к одной стороне, равна (180^circ). Следовательно, (2x+2y=180^circ), или (2(x+y)=180^circ), откуда (x+y=90^circ).
Так как сумма углов в треугольнике равна (180^circ), то (x+y+alpha=180^circ), откуда (alpha=180^circ-(x+y)=180^circ-90^circ=90^circ).
Ответ: 90
Задание
14
#3679
Уровень задания: Равен ЕГЭ
Биссектриса тупого угла параллелограмма делит противоположную сторону в отношении (4:3), считая от вершины острого угла. Найдите большую сторону параллелограмма, если его периметр равен (88).
Из условия задачи следует, что (AK:KD=4:3). Обозначим (AK=4x), (KD=3x). Следовательно, (AD=7x).
Так как в параллелограмме противоположные стороны параллельны, то (angle AKB=angle KBC) как накрест лежащие при (ADparallel BC) и секущей (BK). Следовательно, (angle AKB=angle ABK), то есть (triangle ABK) равнобедренный: (AK=AB). Отсюда (AB=4x).
Следовательно, периметр (88=2(4x+7x)) (так как противоположные стороны параллелограмма равны), следовательно, (x=4).
Значит, большая сторона параллелограмма равна (7x=28).
Ответ: 28

УСТАЛ? Просто отдохни
СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Математика профильного уровня
Математика профильного уровня
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Эксперту
Справочник
Карточки
Теория
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
24 мая
Обновлённая панель инструментов
22 мая
Беседы Решу ЕГЭ по подготовке к ЕГЭ
11 мая
Решение досрочных ЕГЭ по всем предметам
5 мая
Обновленный поиск заданий по ключевым словам
1 мая
Новый сервис: можно исправить ошибки!
29 апреля
Разместили актуальные шкалы ЕГЭ — 2023
24 апреля
Учителю: обновленный классный журнал
7 апреля
Новый сервис: ссылка, чтобы записаться к учителю
30 марта
Решения досрочных ЕГЭ по математике
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Задания
Версия для печати и копирования в MS Word
Тип 1 № 27823
i
Найдите угол между биссектрисами углов параллелограмма, прилежащих к одной стороне. Ответ дайте в градусах.
Спрятать решение
Решение.
Cумма углов, прилежащих к одной стороне параллелограмма, равна
Тогда искомый угол равен
Ответ: 90.
Кодификатор ФИПИ/Решу ЕГЭ:
5.1.2 Параллелограмм, прямоугольник, ромб, квадрат;
5.5.1 Величина угла, градусная мера угла.
Спрятать решение
·
Видеокурс
·
Помощь
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023