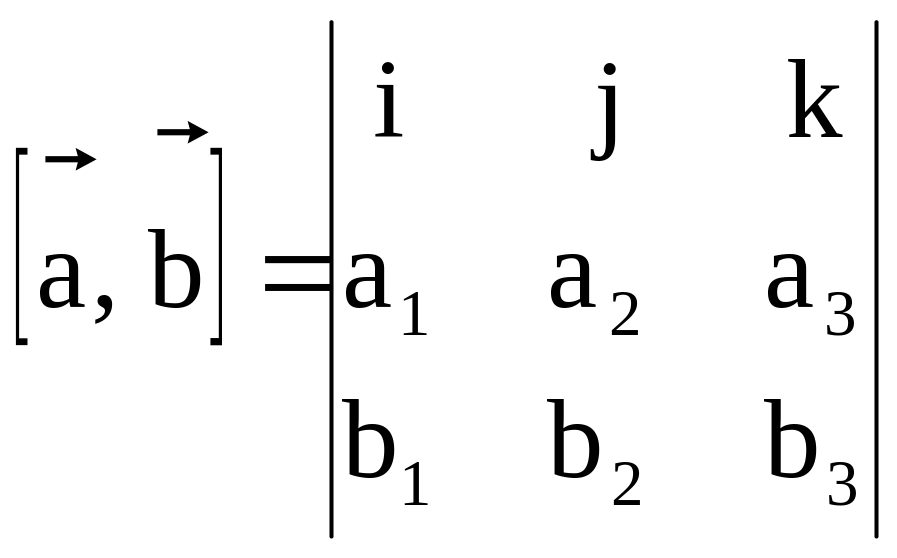Как найти угол между диагоналями параллелограмма векторы - Исправление недочетов и поиск решений вместе с Examum.ru

Математический портал

Nav view search

Navigation

Search

Вы здесь:
Home
Векторная алгебра.
Скалярное произведение векторов, свойства. Длина вектора. Угол между векторами.

Скалярное произведение векторов, свойства. Длина векторов. Угол между векторами.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Длина вектора.

Пусть вектор $overline a=(x, y, z)$ представлен своими координатами в прямоугольном базисе. Тогда его длину можно вычислить по формуле $$|overline a|=sqrt.$$

Скалярное произведение векторов.

Если заданы координаты точек $A(x_1, y_1, z_1) $ и $B(x_2, y_2, z_2),$ то координаты вектора $overline$ можно найти по формулам $$overline=(x_2-x_1, y_2-y_1, z_2-z_1).$$ Скалярным произведением ненулевых векторов $a_1$ и $a_2$ называется число $$(a_1, a_2)=|a_1||a_2|cos(widehat).$$

Для скалярного произведения наряду с обозначением $(a_1,a_2)$ используется также обозначение $a_1a_2.$

Геометрические свойства скалярного произведения:

1) $a_1perp a_2Leftrightarrow a_1a_2=0$ (условие перпендикулярности векторов).

2) Если $varphi=(widehat),$ то $$0leqvarphi 0; qquadqquad frac <pi>

Алгебраические свойства скалярного произведения:

2) $(lambda a_1)a_2=lambda (a_1 a_2);$

Если векторы $a_1(X_1, Y_1, Z_1)$ и $a_2(X_2, Y_2, Z_2)$ представлены своими координатами в прямоугольном базисе, то скалярное произведение равно $$a_1a_2=X_1X_2+Y_1Y_2+Z_1Z_2. $$

Из этой формулы, в частности, следует формула для определения косинуса угла между векторами:

Решение.

а) $$a_1^2=(a_1, a_1)=|a_1||a_1|cos(widehat)=|a_1|^2=3^2=9.$$

б) $(3a_1-2a_2)(a_1+2a_2);$

Поскольку скалярное произведение зависит от длин векторов и угла между ними, то заданные векторы можно выбрать произвольно учитывая эти характеристики. Пусть $a_1=(3; 0). $ Тогда вектор $a_2,$ имея длину $|a_2|=4,$ и, образуя угол $frac<2pi><3>$ с положительной полуосью оси $OX,$ имеет координаты $x=|a_2|cosfrac<2pi><3>=-frac<4><2>=-2; $

$3a_1-2a_2=3(3;0)-2(-2;2sqrt 3)=(9;0)-(-4; 4sqrt 3)=(13;-4sqrt 3);$

$a_1+2a_2=(3; 0)+2(-2;2sqrt 3) = (3; 0)+ (-4; 4sqrt 3)= (-1; 4sqrt 3).$

$(3a_1-2a_2)(a_1+2a_2)=(13; -4sqrt 3)(-1; 4sqrt 3) =-13-48=-61.$

в) $(a_1+a_2)^2.$

$a_1+a_2$=$(3; 0)+(-2; 2sqrt 3)=(1; 2sqrt 3).$

$(a_1+a_2)^2=(1; 2sqrt3) (1; 2sqrt 3)=1+12=13.$

Ответ: a) 9; б) -61; в) 13.

2.67. Вычислить длину диагоналей параллелограмма, построенного на векторах $a=p-3q, $ $b=5p+2q,$ если известно, что $|p|=2sqrt<2>, |q|=3, (widehat)=frac<pi><4>.$

Решение.

Способ 1.

Из треугольника $ABC$ имеем $AC=AB+BC=a+b=p-3q+5p+2q=6p-q.$

Зная длину векторов $p$ b $q$ и угол между этими векторами, можно найти длину вектора $AC$ по теореме косинусов:

Из треугольника $ABD$ имеем: $BD=AD-AB=b-a=5p+2q-p+3q=4p+5q.$

По теореме косинусов находим длину вектора $BD:$

$|BD|^2=|4p|^2+|5q|^2-8p5qcos widehat<(6p, q)>=$ $128+225+240=593.$

Пусть $q=(3; 0). $ Тогда вектор $p,$ имея длину $|p|=2sqrt 2,$ и образуя угол $frac<pi><4>$ с положительной полуосью оси $OX$ имеет координаты

Из треугольника $ABC$ имеем

Из треугольника $ABD$ имеем

$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q=$ $=4(2; 2)+5(3;0)=(8; 8)+(15; 0)=(23; 8).$

Ответ: $15, sqrt <593>.$

2.68. Определить угол между векторами $a$ и $b$ если известно, что $(a-b)^2+(a+2b)^2=20$ и $|a|=1, |b|=2.$

Ответ: $2pi/3$

$|a_1|=3; |a_2|=5. $ Определить, при каком значении $alpha$ векторы $a_1+alpha a_2$ и $a_1-alpha a_2$ будут перпендикулярны.

Ответ: $alpha=pmfrac<3><5>$

В треугольнике $ABC$ $overline=3e_1-4e_2;$ $overline=e_1+5e_2.$ Вычислить длину его высоты $overline,$ если известно, что $e_1$ и $e_2$ взаимно перпендикулярные орты.

Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 ?

Математика | 10 — 11 классы

Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 .

d1 = 2m + n + m — 2n = 3m — n

|d1|² = (3m — n)(3m — n) = 9m² — 6mn + n² = 9|m|² — 6|m||n|cosa + |n|² = 9 * 1 — 6 * 1 * 1 * 1 / 2 + 1 = 9 — 3 + 1 = 7

d2 = 2m + n — m + 2n = m + 3n

|d2|² = (m + 3n(m + 3n) = m² + 6mn + 9n² = |m|² + 6|m||n|cosa + 9|n|² = 1 + 6 * 1 * 1 * 1 / 2 + 9 * 1 = 1 + 3 + 9 = 13.

Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение?

Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение.

Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а?

Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а.

Найдите координаты вектора единичной длины, коллинеарного прямой 3x — 2y + 1 = 0?

Найдите координаты вектора единичной длины, коллинеарного прямой 3x — 2y + 1 = 0.

Дан параллелограмм ABCD?

Дан параллелограмм ABCD.

Найдите сумму векторов вектор АВи АD.

Вычислить длину вектора а?

Вычислить длину вектора а.

Найдите а вектор * в вектор если угол между векторами равен 45° ?

Найдите а вектор * в вектор если угол между векторами равен 45° .

Вектор а = √2, вектор в = 6.

Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей?

Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей.

Назовите вектор с началом О , равный вектору — OD.

Дана система координат Oe1e2 , причем |e1| = 2, |e2| = корень из 3 , угол между ними равен 5pi / 6 ?

Дана система координат Oe1e2 , причем |e1| = 2, |e2| = корень из 3 , угол между ними равен 5pi / 6 .

Найти угол между векторами a(1 ; 2) и b(2 ; 2) и площадь параллелограмма, построенного на векторах a и b.

Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°?

Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°.

Дан параллелограмм ABCD?

Дан параллелограмм ABCD.

Выразите вектор ba через векторы bc и ac.

На этой странице сайта размещен вопрос Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 ? из категории Математика с правильным ответом на него. Уровень сложности вопроса соответствует знаниям учеников 10 — 11 классов. Здесь же находятся ответы по заданному поиску, которые вы найдете с помощью автоматической системы. Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по заданной теме. На этой странице можно обсудить все варианты ответов с другими пользователями сайта и получить от них наиболее полную подсказку.

1 км = 1000 м 1) 160 + 140 = 300(м) — прошли два пешохода вместе 2) 1000 — 300 = 700 (м).

1)999999 2)100000 3)1 шестизначные числа, это числа в которых 6 цифр. Большое 999999, маленькое 100000. Чётные это числа например : 2 4 6 8 10 12 14 16 18 20 22 24. Нечётные : 1 3 5 7 9 11 13 15 17 19 21 23 25. Четные и нечетные они называются на..

999999 111111 1 (999999 — 111111) / 1 = 888888 999999 — (111111 * 1) = 888888 (999999 / 1) + (111111 * 1) = 1111110 Вроде так, но на счет 8 все равно не въеду.

80 : 4 = 20 литров в 1 канистру 20 * 3 = 60 литров в 3 канистры 100 : 20 = 5 канистр для 100 литров.

80 : 4 = 20 л в 1 канистру 20 * 3 = 60 литров в 3 канистры 100 : 20 = 5 канистр для 100 литров бензина.

23 × 12 = 46 23 = 276. Как — то так.

Какой Скажи Пожалуйста.

1) 300 + 150 = 450 (кг) — шерсти всего 2) 150 / 450 = 1 / 3 — сост. Козья шерсть Ответ : 1 / 3.

6х — 14, 7 = 22, 05 6х = 22, 05 + 14, 7 6 * х = 36, 75 х = 36, 75 : 6 х = 6, 125 — это первый 7, 48 — 16х = 2, 68 16х = 7, 48 — 2, 68 16 * х = 4, 8 х = 4, 8 : 16 х = 0, 3.

21 — 10 = 11(шт) — платформы 11×2 = 22(шт) Ответ : В составе товарного поезда всего 22 крытых вагона.

Применение векторов к решению задач

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

На данном уроке мы рассмотрим применение векторов для решения различных геометрических задач, вспомним и докажем некоторые геометрические факты.

Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Векторы и координаты»

источники:

http://matematika.my-dict.ru/q/320401_vycislite-dliny-diagonalej-parallelogramma-postroennogo-na/

http://interneturok.ru/lesson/geometry/8-klass/vektory/primenenie-vektorov-k-resheniyu-zadach

Источник

Условие

1. На векторах a = (9,1,1) и b = (1,1,9) построен параллелограмм.
Найти:
а) угол между диагоналями параллелограмма;
в) высоту параллелограмма, опущенную на вектор b.

математика 10-11 класс
3269

Решение

★

По правилу сложения и вычитания векторов, одна диагональ является суммой векторов, вторая разностью.
vector{d_(1)}=vector{a}+vector{b}=(10;2;10)
vector{d_(2)}=vector{a}-vector{b}=(8;0;-8)

vector{d_(1)}*vector{d_(2)}=10*8+2*0+10*(-8)=0
Скалярное произведение равно 0, значит диагонали параллелограмма взаимно перпендикулярны, угол между диагоналями 90^(o)

S=(1/2)d_(1)*d_(2)

|vector{d_(1)}|=sqrt(10^2+2^2+10^2)=sqrt(204)=2sqrt(51)
|vector{d_(2)}|=sqrt(8^2+0^2+(-8)^2)=8sqrt(2)

S=(1/2)*2sqrt(51)*8sqrt(2)=8sqrt(102)

С другой стороны
S=b*h
|vector{b}|=sqrt(1^2+1^2+9^2)=sqrt(83)
h=8sqrt(102)/sqrt(83)

Написать комментарий

Источник

Как найти угол между диагоналями параллелограмма

Прежде чем искать решение поставленной задачи, следует выбрать наиболее подходящий метод ее решения.Геометрический метод требует тдополнительных построений и их обоснования, поэтому в данном случае наиболее удобным представляется использование векторной методики. Для этого используются направленные отрезки — векторы.Вам понадобится

Пусть параллелограмм задан векторами двух его сторон (остальные две попарно равны) в соответствии срис. 1. Вообще-то равных векторов на плоскости сколь угодно много. Для этого требуется равенство их длин (точнее модулей – |a|) и направления, которое задается наклоном к какой-либо оси (в декартовыхкоординатах это ось 0Х).Поэтому для удобства взадачах подобного типа векторы, как правило, задают их радиус-векторами r=а, у которых начало всегда лежит в начале координат.

Для нахождения угла между сторонами параллелограмма понадобится вычислить геометрическую сумму и разность векторов, а также их скалярное произведение (a,b). По правилу параллелограмма геометрическая сумма векторов a и b равна некоторому вектору с=а+b, который построен и лежит на диагонали параллелограмма AD. Разность a и b – вектор d=b-a, построенный на второй диагонали BD. Если векторы заданы координатами, а угол между ними составляет ф,тогда их скалярное произведение – это число, равное произведению модулей векторов и cosф (см. рис1): (a, b) = |a||b|cos ф

В декартовых координатах если а={x1, y1} иb={x2, y2}, то (a, b) = x1y2 +x2y1.При этом скалярный квадрат вектора (а,а)=|a|^2=x1^2 +x2^2.Для вектора b – аналогично. Тогда: |a||b|cos ф = x1y2 +x2y1. Следовательноcosф=(x1y2 +x2y1)/(|a||b|).Таким образом алгоритм решения задачи состоит в следующем:1. Нахождение координат векторов диагоналей параллелограмма как векторов суммы и разности векторов его сторон с=а+b и d=b-a. При этом соответствующие координаты a и b просто складываются или вычитаются. c= a+ b ={x3, y3}= { x1+x2, y1+y2},d= b-a ={x4, y4}={ x2 –x1, y2-y1}.2. Нахождение косинуса угла между векторами диагоналей (назовем его фД) по приведенному общемуправилу cosфд=(x3y3 +x4y4)/(|c||d|)

Пример. Найти угол между диагоналями параллелограмма, заданного векторами своих сторон a={1, 1} и b ={1, 4}. Решение. Согласно приведенному алгоритму вам необходимо найти векторы диагоналей c={1+1, 1+4}={2, 5}иd={1-1, 4-1}={0, 3}. Теперь вычислите cosфд =(0+15)/(sqrt(4+25)sqrt9)= 15/3sqrt29=0,92.Ответ:фд= arcos(0,92).

Источник

Примеры решения задач

Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах

и

,
где

таковы, что

.

Решение.
Диагонали параллелограмма есть векторы

и

.
Вычислим длину вектора

:

.

Аналогично
вычисляется длина вектора

.

Задача 2.
Найдите вектор

,
коллинеарный вектору

и удовлетворяющий условию

.

Решение.
Обозначим вектор

,
тогда из условий задачи

или

,

тогда

.
Итак:

.

Задача 3.
Найти проекцию вектора

на направление вектора

.

Решение.

.
По формуле проекции вектора на ось будет
иметь место равенство

Задача 4.
Даны векторы:

.

П
роверить,
есть ли среди них коллинеарные. Найти

.

Решение.
Условие коллинеарности имеет вид

.
Этому условию удовлетворяют векторы

.
Следовательно, они коллинеарны. Найдем
длины

векторов

:

Угол между векторами
определяется по формуле

.

огда

,

Используя формулу

,
получим

.

Задача 5.
На материальную точку действуют силы

.
Найти работу равнодействующей этих сил

при перемещении точки из положения

в положение

.

Решение.
Найдем силу

и вектор перемещения

.

,
тогда искомая работа

.

Задачи

1. Векторы

взаимно перпендикулярны, а вектор

образует с ними углы

.
Зная, что

,
найти: 1)

;
2)

.

2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах

,
если известно, что

.

3. Доказать, что
вектор

перпендикулярен к вектору

4. Зная, что

,
определить, при каком значении коэффициента

векторы

окажутся перпендикулярными.

5. Даны вершины
четырехугольника:

.
Доказать, что его диагонали взаимно
перпендикулярны.

6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах

.

7. Даны силы

.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку

.

8. Даны вершины
треугольника:

.
Найти проекцию вектора

на вектор

9. Найти вектор

,
перпендикулярный векторам

,
если известно, что его проекция на вектор

равна единице.

10. Сила, определяемая
вектором

,
разложена по трем направлениям, одно
из которых задано вектором

.
Найти составляющую силы

в направлении вектора

11. Даны вершины
треугольника:

.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.

12. Даны три
последовательные вершины параллелограмма:

.
Найти его четвертую вершину D
и угол между векторами

.

13. На оси

найти точку, равноудаленную от точек

.

14. Доказать, что
треугольник с вершинами

прямоугольный.

Домашнее задание

1. Вычислить
скалярное произведение двух векторов

,
зная их разложение по трем единичным
взаимно перпендикулярным векторам

;

2. Найти длину
вектора

,
зная, что

– взаимно перпендику-

лярные орты.

3. Векторы

попарно образуют друг с другом углы,
каждый из которых равен

.
Зная, что

,
определить модуль вектора

.

4. Доказать, что
вектор

перпендикулярен к вектору

5. Даны векторы

,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису

.

6. Вычислить угол
между векторами

,
где

—
единичные взаимно перпендикулярные
векторы.

7. Даны силы

,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения

в положение

.

8. Даны вершины
треугольника

.
Определить его внутренний угол при
вершине В.

9. Вычислив
внутренние углы треугольника с вершинами

,

,
убедиться, что этот треугольник
равнобедренный.

10. Найти вектор

,
зная, что он перпендикулярен векторам

и

.

11. Найти вектор

,
коллинеарный вектору

и удовлетворяющий условию

,
где

.

12. Вычислить
проекцию вектора

на ось вектора

.

13. Даны векторы

.
Вычислить

.

14. Даны точки

.
Вычислить проекцию вектора

на ось вектора

.

Ответы к задачам

1) -7, 13. 2) 15,

.
4)

.
6)

.
7) 2. -1/3.

9)

.
10)

.
11)

.

12)

.
13)

.

Ответы к домашнему
заданию

1) 9. 2) 5. 3) 10. 5)

.
6)

.
7) 13.

10)

.
12) 6. 13) 5. 14) 3.

Занятие 3

Векторое
произведения векторов. Смешанное
произведение векторов

Определение1.
Тройка
некомпланарных векторов

называется правой (левой) если, находясь
внутри телесного угла, образованного
приведенными к общему началу векторами

и от него к

,
човершающимся против часовой стрелки
(по часовой стрелке)

Тройка правая
Тройка левая

Определение
2. Векторным
произведением вектора

на вектор

называется вектор

,
длина и направление которого определяются
условиями:

1.

,
где

— угол между

.

2.

.

— правая тройка векторов.

Свойства
векторного произведения

(свойство антиперестановочности
сомножителей);

(распределительное относительно суммы
векторов);

(сочетательное относиельно числового
множителя);

(равенство нулю векторного произведения
означает коллинеарность векторов);

5.

,
т. е. момент сил равен векторному
произведению силы на плечо.

Если вектор

,
то

.

Определение
3. Смешанным
произведением

трех векторов называется число,
определяемое следующим образом:

.
Если векторы заданы своими координатами:

,
то

~

.

Свойства
смешанного произведения

1. Необходимым и
достаточным условием компланарности
векторов

является равенство

= 0.

2. Объем
параллелепипеда, построенного на
векторах

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Найти угол между диагоналями параллелограмма, построенного на векторах как на сторонах, если

Рассм. рав-во , из к-рого и опр-м ;

Вычислим

;

Задача 3 Вычислить проекцию вектора на ось вектора , Если

Рассм. ;

Вычислим ;

Задача 4 Определить, при каком векторы будут взаимно перпендикулярными.

Рассм. .

Задача 5 Найти момент силы, приложенной в точке относительно точки , а также модуль и направляющие косинусы вектора силы

1) , где ;

;

2) ; направл. косинусы вектора :

Задача 6 Найти координаты вектора , если он перпендикулярен векторам , Образует острый угол с осью и .

Пусть , причём ( т. к. Образует острый угол с осью OZ );

;

Решим с-му ур-й (1) – (3) и опр-м координаты вектора : но ,

След. выбираем , т. е. и ; .

Задача 7 При каком значении точки будут лежать в одной плоскости?

Рассм. векторы ;

Рассм. смешанное произведение ; след.

При векторы компланарны и точки лежат в одной плоскости.

Задача 8 В треугольнике найти координаты центра тяжести, длину и уравнение медианы , если известны координаты вершин треугольника:

1) Определим координаты точки (середины отрезка ):

; ; ;

2) составим ур – е прямой : ;

3) ;

4) координаты т.Пересечения медиан в (центр масс) определим из условия, что т.Делит отрезок в отношении 2:1, т. е. ; .

Задача 9 Составить уравнения сторон ромба и найти его площадь, если известны уравнения сторон и координаты вершины

1) Составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

2) составим уравнение стороны как прямой, проходящей через точку Параллельно

Прямой ;

3) определим площадь ромба :

Определим координаты точки как точки пересечения прямых :

;

Определим координаты точки как точки пересечения прямых :

;

Рассм. векторы: ; рассм. векторное произведение:

Площадь ромба равна: .

Задача 10 Составить уравнение плоскости, проходящей через точки параллельно оси

Пусть — искомая плоскость;

Рассм. вектор ; рассм. направл. вектор оси ;

Рассм. норм. вектор

Рассм. произв. т. и рассм. вектор ; , т. е. ; .

Задача 11 Через точку провести прямую , параллельную двум плоскостям: .

Рассм. норм. векторы ;

Рассм. направл. вектор прямой : ;

Рассм. ; запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. А параллельно вектору : ; параметрические ур-я прямой :

Задача 12 Найти проекцию точки на прямую , заданную как пересечение двух плоскостей:

Рассм. норм. векторы ; рассм. направл. вектор прямой :

;

Рассм. ; определим какую-либо точку ;

Рассм. Положим , тогда ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. параллельно вектору : ; параметрические ур-я прямой :

Рассм. плоскость , проходящую через точку перпендикулярно прямой : ;

Рассм. произв. т. и рассм. вектор ;

, т. е. ;

Найдём теперь искомую проекцию точки на прямую как точку пересечения плоскости и прямой : ; .

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке:

1) Непосредственное вычисление:

;

2) Разложение по 1-й строке:

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы.

Запишем данную систему уравнений в матричной форме: , (1) , где ; ; ;

Рассм. опред-ль матрицы : ,

След., матр. — невырожденная и можно применять формулы Крамера и вычислять обратную матр. ;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул:

, , , где ,

, , ;

реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. : , след., матр.— невырожденная и существует обратная матр. ; умножим рав-во (1) слева на матрицу :