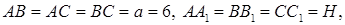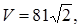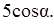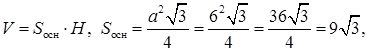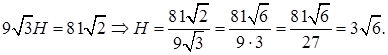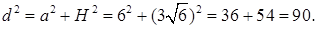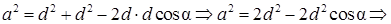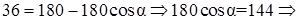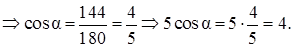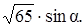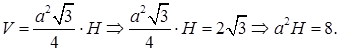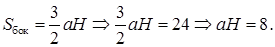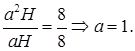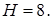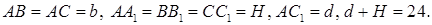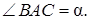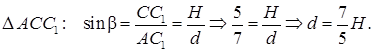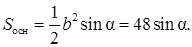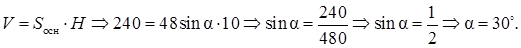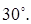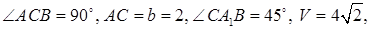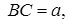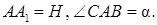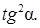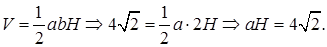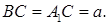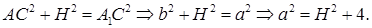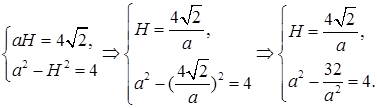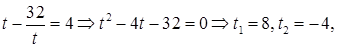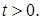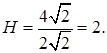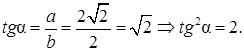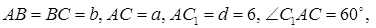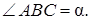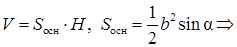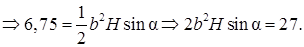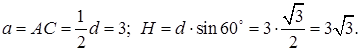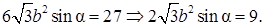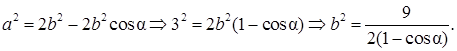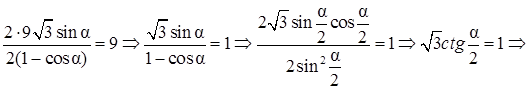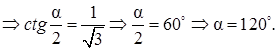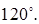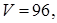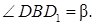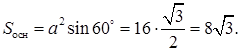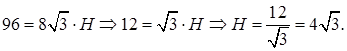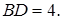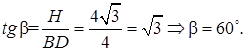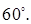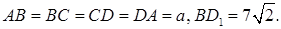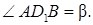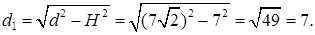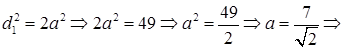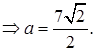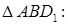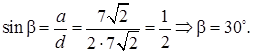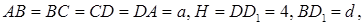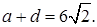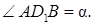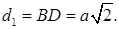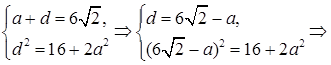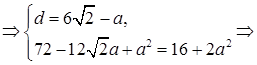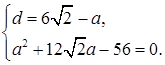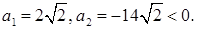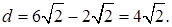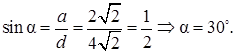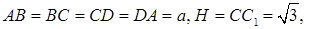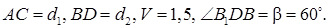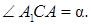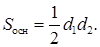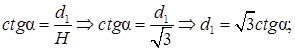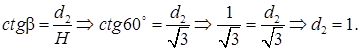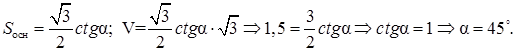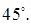Как найти угол между диагональю прямоугольного параллелепипеда

Как решить задачу (см.)?

Стороны основания прямоугольного параллелепипеда равны 6м и 8м,боковое ребро равно 10м. Найдите угол между диагональю параллелепипеда и плоскостью его основания.

Прямоугольный параллелепипед показан на рисунке.

Имеем b = 6 м, а = 8 м и с = 10м. Найти угол между диагональю параллелепипеда d =AG и плоскостью его основания ABCD, то есть угол между диагоналями AG и АС. (На рисунке диагональ АС не нарисована). Вначале найдем длину диагонали АС = sqrt(a^2 + b^2) = sqrt(8^2 + 6^2) = sqrt(64 + 36) = sqrt(100) = 10 м. (На рисунке диагональ АС не прочерчена, на своем рисунке прочертите ее для наглядности). Значок sqrt означает квадратный корень (от английских слов square root). Математический знак корня БВ не понимает, поэтому ставит вместо него знак вопроса ?). БВ не понимает ни греческие буквы, ни математические знаки, которых нет на клавиатуре. Итак, АС = 10 м. Имеем прямоугольный треугольник АСG. Теперь легко найти угол CAG в этом треугольнике CAG. Угол GCA будет прямоугольным (90°), так как ребро GC в параллелепипеде перпендикулярно основанию ADCB. Из прямоугольного треугольника AGC находим тангенс угла GAC. При этом заметим, GC = с = 10 м, так как оба эти катета – высота параллелепипеда. Имеем tg(GAC) = GC/AC = 10/10 = 1. А если тангенс равен 1, то это угол в 45°. Ответ 45°.

Диагональ параллелепипеда

Геометрический калькулятор для прямоугольного параллелепипеда можно запустить также, зная два из трех ребер тела и его диагональ. Поскольку диагональ параллелепипеда равна по теореме Пифагора квадратному корню из суммы квадратов всех трех его ребер, то из этого выражения алгебраически можно вывести формулу для третьего неизвестного ребра. (рис.22.4) d_4=√(a^2+b^2+c^2 ) b=√(a^2+c^2-〖d_4〗^2 )

Имея возможность вычислить неизвестное ребро параллелепипеда, можно следом найти все остальные диагонали его боковых граней. (рис.22.1, 22.2, 22.3) d_1=√(a^2+c^2 ) d_2=√(a^2+b^2 )=√(a^2+a^2+c^2-〖d_4〗^2 )=√(2a^2+c^2-〖d_4〗^2 ) d_3=√(b^2+c^2 )=√(a^2+c^2-〖d_4〗^2+c^2 )=√(a^2+2c^2-〖d_4〗^2 )

Чтобы найти угол α между диагональю прямоугольного параллелепипеда и диагональю его основания, необходимо воспользоваться отношением синуса — известного бокового ребра а к диагонали параллелепипеда. (рис.22.5) sin⁡α=a/d_4

Периметр прямоугольного параллелепипеда равен учетверенной сумме ребер, составляющих параллелепипед. Для неизвестного ребра в формулу подставляется полученное из теоремы Пифагора выражение через диагональ параллелепипеда. P=4(a+b+c)

Площадь полной поверхности прямоугольного параллелепипеда через диагональ также можно вычислить посредством замены неизвестной переменной на соответствующее выражение. Изначально площадь параллелепипеда равна удвоенной сумме попарных произведений его ребер. S=2(ab+bc+ac)=2((a+c) √(a^2+c^2-〖d_4〗^2 )+ac)

Чтобы найти объем прямоугольного параллелепипеда, зная диагональ, нужно умножить два известных ребра параллелепипеда на квадратный корень из разности квадрата диагонали от суммы квадратов этих ребер. V=abc=ac√(a^2+c^2-〖d_4〗^2 )

Примеры с решениями

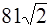
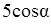
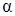
7.1Объем правильной треугольной призмы равен , сторона основания равна 6. Найти , где – угол между диагоналями двух боковых граней, проведенными из одной и той же вершины (рис. 7.1).

Решение. Дано: 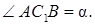Найти

то для нахождения ребра H получаем уравнение

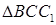
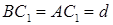
Применив теорему Пифагора, из найдем диагональ боковой грани

Теперь к 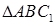применим теорему косинусов и получим уравнения для нахождения .

7.2 Основанием прямой призмы является равносторонний треугольник.

Объем призмы равен , площадь ее боковой поверхности равна 24. Вычислить , где — угол наклона диагонали боковой грани к плоскости основания (рис.7.2).

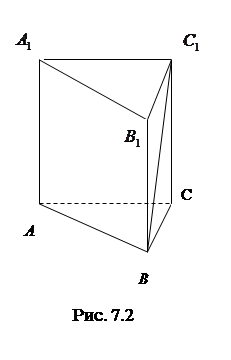
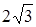
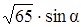
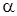
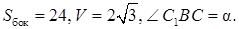
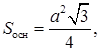
Решение. Дано: Найти

поэтому

Получаем систему уравнений и решаем ее делением первого уравнения на второе. Получаем

Тогда ребро (высота) призмы

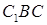
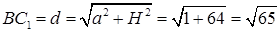
Из треугольника находим диагональ боковой грани

и

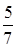
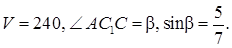
7.3 Основанием прямой призмы является равнобедренный треугольник. Объем призмы равен 240. Диагональ одной из равных боковых граней наклонена к плоскости основания под углом, синус которого равен . Сумма длин этой диагонали и высоты призмы равна 24. Найти (в градусах) угол при вершине основания (рис.7.3).

Решение. Дано: Найти

Решаем систему уравнений

Тогда Из найдем

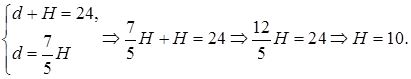
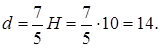
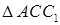
Площадь основания призмы

Ответ:

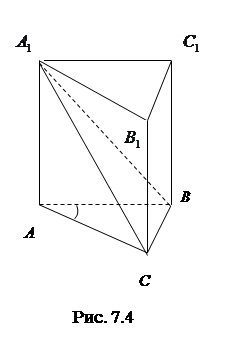
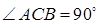
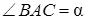
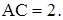
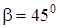
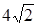
7.4Основанием прямой призмы является прямоугольный треугольник ABC, у которого , и катет Диагональ боковой грани призмы, проходящей через гипотенузу AB, образует с боковой гранью, проходящей через катет AC, угол . Найти , если объем призмы равен (рис.7.4).

Решение. Дано:

Найти

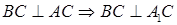
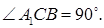
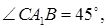
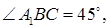
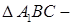
Согласно условию (по теореме о трех перпендикулярах), следовательно, Далее, поэтому и а это означает, что прямоугольный и равнобедренный, в нем

Решаем систему уравнений:

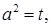
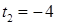
Во втором уравнении системы положим в результате чего уравнение приведется к виду

не удовлетворяет условию

Получаем, что 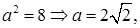поэтому

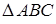
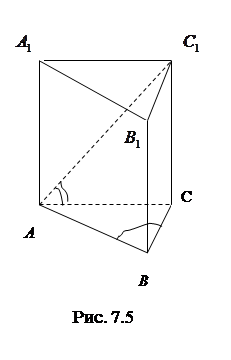
Из находим

7.5Основанием прямой призмы является равнобедренный тупоугольный треугольник. Диагональ боковой грани, противолежащей тупому углу основания, равна 6 и составляет с плоскостью основания угол 60 0 . Найти ( в градусах) тупой угол основания, если объем призмы равен 6,75 (рис 7.5).

Решение. Дано: 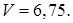Найти тупой

поэтому

Далее, к треугольнику 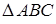применим теорему косинусов:

Ответ:

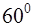
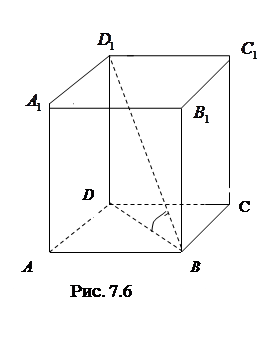
7.6 Основанием прямого параллелепипеда является ромб со стороной, равной 4, и острым углом . Объем параллелепипеда равен 96. Найти (в

градусах) угол наклона меньшей диагонали параллелепипеда к плоскости основания (рис. 7.6).

Решение. Дано:

Найти

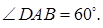
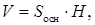
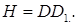
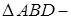
Объем призмы где Найдем

равносторонний, поэтому

Из 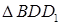найдем

Ответ:

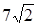
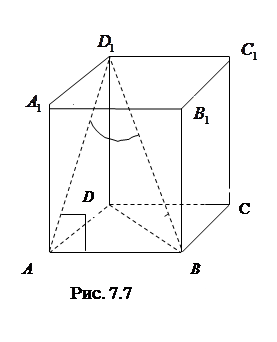
7.7 Основанием прямого параллелепипеда является квадрат. Длина бокового ребра равна 7. Найти ( в градусах) угол между диагональю параллелепипеда и боковой гранью, если диагональ параллелепипеда равна (рис. 7.7).

Решение. Дано:

Найти

Из найдем

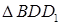
Из прямоугольного 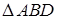находим, что

Рассмотрим

Ответ:

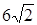
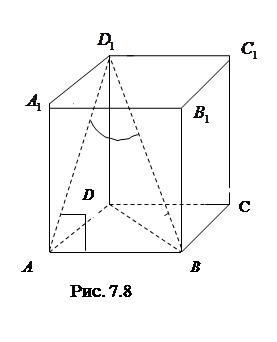
7.8Основанием прямоугольного параллелепипеда является квадрат. Высота параллелепипеда равна 4. Сумма диагонали параллелепипеда и стороны основания равна . Найти ( в градусах) угол между диагональю параллелепипеда и его боковой гранью (рис. 7.8).

Решение. Дано:

Найти

Диагональ квадрата

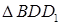
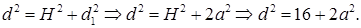
Из найдем Решаем систему

Решая квадратное уравнение, находим

Из прямоугольного 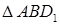находим

Ответ:

7.9Основанием прямого параллелепипеда является ромб. Объем параллелепипеда равен 1,5 и его высота равна . Найти (в градусах) угол наклона к плоскости основания большей диагонали параллелепипеда, если его меньшая диагональ наклонена к плоскости основания под углом (рис. 7.9).

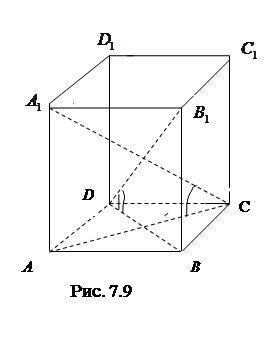
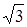
Решение. Дано:

Найти

Так как диагонали ромба взаимно перпендикулярны, то

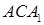
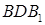
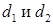
Из треугольников и выразим диагонали соответственно:

Ответ: