Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами
Доказательства теорем об углах, связанных с окружностью
Теорема 1 . Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство . Рассмотрим сначала вписанный угол ABC , сторона BC которого является диаметром окружности диаметром окружности , и центральный угол AOC (рис. 5).
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).
В этом случае справедливы равенства
и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).
В этом случае справедливы равенства
что и завершает доказательство теоремы 1.
Теорема 2 . Величина угла, образованного пересекающимися хордами хордами , равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство . Рассмотрим рисунок 8.
Нас интересует величина угла AED , образованного пересекающимися в точке E хордами AB и CD . Поскольку угол AED – внешний угол треугольника BED , а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 3 . Величина угла, образованного секущими секущими , пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство . Рассмотрим рисунок 9.
Нас интересует величина угла BED , образованного пересекающимися в точке E секущими AB и CD . Поскольку угол ADC – внешний угол треугольника ADE , а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 4 . Величина угла, образованного касательной и хордой касательной и хордой , проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство . Рассмотрим рисунок 10.
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр , проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать
Теорема 5 . Величина угла, образованного касательной и секущей касательной и секущей , равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство . Рассмотрим рисунок 11.
Нас интересует величина угла BED , образованного касательной AB и секущей CD . Заметим, что угол BDC – внешний угол треугольника DBE , а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB , в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать.
Теорема 6 .Величина угла, образованного двумя касательными к окружности касательными к окружности , равна половине разности величин дуг, заключённых между его сторонами.
Доказательство . Рассмотрим рисунок 12.
Нас интересует величина угла BED , образованного касательными AB и CD . Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство
Углы, связанные с окружностью.
Центральный угол — угол, вершина которого совпадает с центром окружности.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают её.
Вписанный угол в два раза меньше центрального , опирающегося на ту же дугу.
Все вписанные углы , опирающиеся на одну и ту же дугу равны.
Все вписанные углы , опирающиеся на одну и ту же хорду, вершины которых лежат по одну сторону от этой хорды, равны.
Все вписанные углы , опирающиеся на диаметр, прямые.
Любые два вписанных угла , опирающиеся на одну и ту же хорду, вершины которых лежат по разные стороны хорды, составляют в сумме 180°.
Угол между пересекающимися хордами измеряется полусуммой дуг, заключенных между его сторонами.
Угол между секущими, пересекающимися вне окружности, измеряется полуразностью дуг, заключенных между его сторонами.
Угол между касательной и секущей, пересекающимися вне окружности, измеряется полуразностью дуг, заключенных между его сторонами.
Угол между касательными к окружности измеряется полуразностью дуг, заключенных между его сторонами.
Угол между касательной и хордой, проходящей через точку касания, равняется половине центрального угла, опирающегося на данную хорду:
Центральные и вписанные углы
О чем эта статья:
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине дуги, на которую опирается.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC — центральный, угол ABC — вписанный. Оба угла опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу AB. ㄥACB = ?
Как решаем: окружность 360° − AC − CB = 360° − 200° − 80° = 80°
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360° = 72°
Вписанный угол равен половине дуги, поэтому ㄥCAB = ½ от CB = 72° / 2 = 36°
http://anasta8ia.ru/angles-associated-with-the-circle/
http://skysmart.ru/articles/mathematic/centralnye-i-vpisannye-ugly
Угол между касательными.
В этой статье мы рассмотрим, как решать задачи на нахождение угла между касательными.
Угол между касательными.
Пусть дана функция 

Угол между прямыми — это меньший из двух углов, образованных этими прямыми. В нашем случае это угол 
Чтобы найти угол 
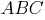
В треугольнике 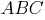


Но угол 



Угол 
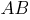


Итак,
Мы помним, что угол между прямыми всегда острый, и его тангенс должен быть больше нуля. В общем случае 
формула для нахождения тангенса угла между касательными 

Решим задачу:
Найти тангенс большего угла между касательными, проведенными из точки 

Заметим, что в этой задаче нужно найти тангенс большего угла между касательными, то есть тангенс тупого угла. Тангенсы смежных углов равны по модулю, но противоположны по знаку. Следовательно, нам нужно найти тангенс угла между касательными, и в ответе записать это значение со знаком «-«.
Нужно найти коэффициенты наклона касательных, проведенных к параболе из точки 


Вспомним, как находить уравнение касательной, проведенной к графику функции 
Пусть 
Уравнение касательной, проведенной из точки 
Подставим выражения для 


Решим это уравнение. Упростим правую часть:
Итак, мы нашли абсциссы точек касания:
Найдем коэффициенты наклона касательных, проведенных к параболе 
Тангенс большего угла между касательными равен
Ответ: -4
И.В. Фельдман, репетитор по математике.
Если две окружности касаются внешне, как найти угол между их общими внешними касательными?

Найти: ∠KCM
Решение:
Центры окружностей, точки O1 иO2 и их точка касания D лежат на одной прямой.

(как радиусы, проведённые в точки касания), следовательно, O1A∥O2B и четырёхугольник ABO2O1 — прямоугольная трапеция.
Проведём высоту O2F.
Четырёхугольник ABO2F — прямоугольник (так как у него все углы прямые). Значит, AF=O2B=R-r, O2F=AB=2√Rr.
В прямоугольном треугольнике O1O2F
Обозначим для удобства ∠O1O2F=α. Тогда
∠O1CM=∠O1O2F=α (как соответственные при AB∥FO2 и секущей CO1).
CO1 — биссектриса угла KCM. Значит, ∠KCM=2α.
Если значения синуса, косинуса или тангенса не являются табличными, можно найти синус, косинус или тангенс угла KCM, используя формулы двойного угла.
Например,
Угол KCM равен арктангенсу этой величины.
Как найти угол между касательными
Прямая линия, имеющая с окружностью одну общую точку, является касательной к окружности. Другая особенность касательной – она всегда перпендикулярна радиусу, проведенному в точку касания, то есть касательная и радиус образуют прямой угол. Если из одной точки А проведены две касательных к окружности АВ и АС, то они всегда равны между собой. Определение угла между касательными (угол АВС) производится с помощью теоремы Пифагора.

Инструкция
Для определения угла необходимо знать радиус окружности ОВ и ОС и расстояние точки начала касательной от центра окружности — О. Итак, углы АВО и АСО равны 90 градусов, радиус ОВ, например 10 см, а расстояние до центра окружности АО равно 15 см. Определите длину касательной по формуле в соответствии с теоремой Пифагора: АВ = квадратный корень из АО2 – ОВ2 или 152 — 102 = 225 – 100 = 125;
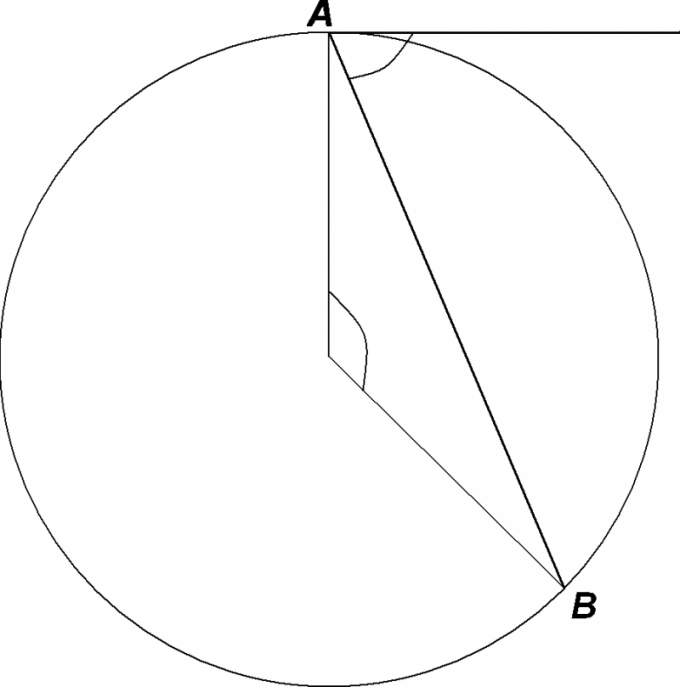
Извлеките квадратный корень. Получится 11.18 см. Поскольку угол ВАО представляет собой sin или отношение сторон ВО и АО вычислите его значение: Sin угла ВАО = 10 : 15 = 0.66
Затем, пользуясь таблицей синусов, найдите данное значение, которое соответствует примерно 42 градусам. Таблица синусов используется для решения различных задач – физических, математических или инженерных. Остается выяснить величину угла ВАС, для чего следует величину данного угла удвоить, то есть, получится примерно 84 градусов.
Величина центрального угла соответствует угловой величине дуги, на которую он опирается. Величину угла можно также определить с помощью транспортира, приложив его к чертежу. Так как подобные вычисления относятся к тригонометрии, то можно воспользоваться тригонометрическим кругом. С его помощью можно переводить градусы в радианы и наоборот.
Как известно, полный круг составляет 360 градусов или 2П радиан. На тригонометрическом круге отображены значения синусов и косинусов основных углов. Стоит напомнить, что значение синуса находится на оси Y, а косинуса на оси Х. Значения синуса и косинуса находятся в промежутке от -1 до 1.
Определить значения тангенса и котангенса угла можно поделив синус на косинус, а котангенса наоборот – косинуса на синус. Тригонометрический круг позволяет определить знаки всех тригонометрических функций. Так, синус — это нечетная функция, а косинус – четная. Тригонометрический круг позволяет понять, что синус и косинус – периодические функции. Как известно, период равен 2П.
Видео по теме
Источники:
- угол между двумя касательными
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.
Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:
$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$
Таким образом, искомая точка $x=1$.
Далее находим производные заданных функций в найденной точке:
$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$
Итак, искомый тангенс:
$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$
Ответ. $operatorname{tg} phi=frac{1}{7}$




























































![Rendered by QuickLaTeX.com [tgangle {rm{KCM}} = frac{{2 cdot frac{{R - r}}{{2sqrt {Rr} }}}}{{1 - {{(frac{{R - r}}{{2sqrt {Rr} }})}^2}}} = frac{{4sqrt {Rr} (R - r)}}{{4Rr - {{(R - r)}^2}}}.]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82c3a601f78337f020aea52fba7c194f_l3.png)