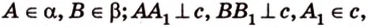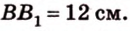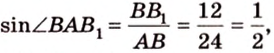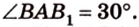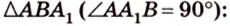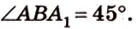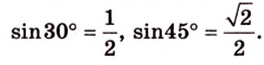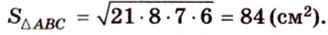|
|
|
|
правила раздела Алгоритмы
1. Помните, что название темы должно хоть как-то отражать ее содержимое (не создавайте темы с заголовком ПОМОГИТЕ, HELP и т.д.). Злоупотребление заглавными буквами в заголовках тем ЗАПРЕЩЕНО.
2. При создании темы постарайтесь, как можно более точно описать проблему, а не ограничиваться общими понятиями и определениями.
3. Приводимые фрагменты исходного кода старайтесь выделять тегами code…/code
4. Помните, чем подробнее Вы опишете свою проблему, тем быстрее получите вразумительный совет
5. Запрещено поднимать неактуальные темы (ПРИМЕР: запрещено отвечать на вопрос из серии «срочно надо», заданный в 2003 году)
6. И не забывайте о кнопочках TRANSLIT и РУССКАЯ КЛАВИАТУРА, если не можете писать в русской раскладке
подскажите формулу как найти угол между двумя отрезками
, …
- Подписаться на тему
- Сообщить другу
- Скачать/распечатать тему
|
|
|
|
Senior Member Рейтинг (т): 15 |
задано 2 отрезка (х1,у1)-(х2,у2) и (х2,у2)-(х3,у3) |
volvo877 |
|
|
И при чем тут Паскаль? Тебе формула нужна? Тогда переезжаем в Алгоритмы… |
|
v1m |
|
|
Senior Member Рейтинг (т): 15 |
сор |
Da$aD |
|
|
Общая точка является концом отрезка, или может быть где угодно? |
|
v1m |
|
|
Senior Member Рейтинг (т): 15 |
не работает( должно в Form1.Caption писать размер угла unit Unit1; interface uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, Math, ExtCtrls; type TForm1 = class(TForm) Timer1: TTimer; procedure FormMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Integer); procedure Timer1Timer(Sender: TObject); private { Private declarations } public { Public declarations } end; const x2=200; y2=200; x1=300; y1=200; var Form1: TForm1; a : single; implementation {$R *.dfm} procedure TForm1.FormMouseMove(Sender: TObject; Shift: TShiftState; X, Y: Integer); var xa,ya,xb,yb : longint; begin xa:=x1-x2; ya:=y1-y2; xb:=x-x2; yb:=y-y2; a:=arccos((xa*xb+ya*yb)/sqrt((sqr(xa)+sqr(ya))*(sqr(xb)+sqr(yb)))); Form1.Caption:=FloatToStr(a); end; procedure TForm1.Timer1Timer(Sender: TObject); begin Canvas.Ellipse(100,100,300,300); Canvas.MoveTo(200,200); Canvas.LineTo(300,200); Timer1.Enabled:=false; end; end. Сообщение отредактировано: v1m — 20.03.10, 18:34 |
|
v1m |
|
|
Senior Member Рейтинг (т): 15 |
я там выложил свой исходник посмотри плиз… |
|
Fts |
|
|
Всё правильно, должно работать, осталось угол в градусы перевести для красоты. |
|
Fts |
|
|
А я вижу только одну ситуацию возможного обрушения |
|
amk |
|
|
Вот еще вариант dx1 = x1 — x2 a = dx1*dy2 — dy1*dx2 θ = arctan (a/b) Со знаком только надо разобраться |
|
andrew.virus |
|
|
Цитата v1m @ 20.03.10, 13:37 задано 2 отрезка (х1,у1)-(х2,у2) и (х2,у2)-(х3,у3)
один из вариантов найти проходящие через отрезки прямые и найти угол между ними … |
|
v1m |
|
|
Senior Member Рейтинг (т): 15 |
сор что не написал что не работает)))) |
|
v1m |
|
|
Senior Member Рейтинг (т): 15 |
не ты меня не так понял ну это уже неважно))) Сообщение отредактировано: v1m — 21.03.10, 18:13 |
0 пользователей читают эту тему (0 гостей и 0 скрытых пользователей)
0 пользователей:
- Предыдущая тема
- Алгоритмы
- Следующая тема
[ Script execution time: 0,0755 ] [ 15 queries used ] [ Generated: 28.05.23, 01:55 GMT ]
Метод координат (углы между векторами и плоскостями)
Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.
Решение задач с доказательством.
Для того, чтобы успешно решать задачи методом координат, полезно помнить:
Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.
Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.
Задача. Найти координаты и длины векторов AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).
AB = (1−5; 0-8; −3−3) = (−4; −8; −6)
AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)
BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)
Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):
Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
- Вычисляем косинус угла между векторами.
- Через основное тригометрическое тождество получаем синус.
- Подставляем в формулу площади.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
Задача. Задайте уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
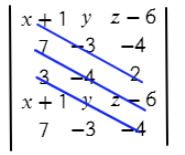
- Задаем матрицу плоскости.
- Вычисляем ее определитель, это и есть уравнение плоскости.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
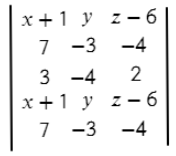
Вторая строчка — координаты первого вектора.
Третья строчка — координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).
Четвертая заполняется аналогично первой.
Пятая — аналогично второй.
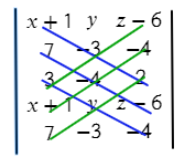
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4)
Аналогично делаем с зелеными отрезками:
(z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7
Осталось из значений синих отрезков вычесть значения зеленых отрезков:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4) − ((z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7) =
= −22х −26y −19z + 92
−22х −26y −19z + 92 — искомое уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета — это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.
Задача. Найдите угол между плоскостью, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6), и плоскостью, заданную уравнением
14x + 6y −27z + 51 = 0.
- Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
- Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).
Будь в курсе новых статеек, видео и легкого математического юмора.
Вроде 64. Т.к. угол лежащий на прямой в два раза меньше дуги на которую опирается
По теореме Пифагора
АС²=AD²+DC²=9+16
AC=5
С1СА=90
по скольку С1АС=45 то АС1С=45 тоже
треугольник АС1С равнобедренный АС=С1С=5
AC1²=AC²+C1C²=25+25
AC1=5√2
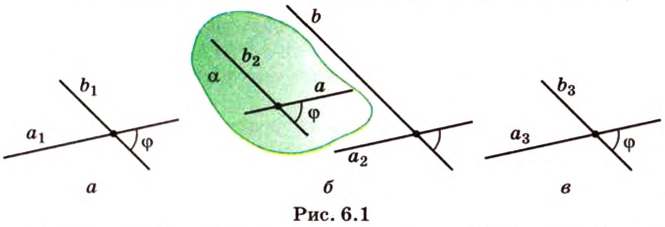
1) а1b1=120°
ab1=60°
2) 2=4=145°
3) mn=120°
4) 3=150°;4=30°
5) 1=3=60°;2=4=120°
6) 4=60°
7) 1=120°;2=3=60°
8)90°+угол1, или, если ОЕ — биссектриса, тогда АОЕ=135°
АD (3-3;-7-1)=(0;-8)
B<span>С(2-5;0-4)=(-3;-4)</span>
Ответ:
=======================
Объяснение:
Содержание:
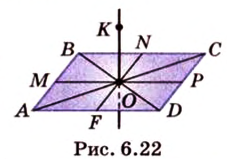
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
Угол между двумя прямыми в пространстве
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 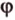
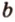
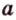
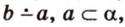
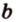
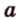
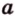
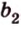
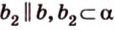
Итак,
Если 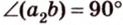
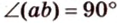
Угол между прямой и плоскостью в пространстве
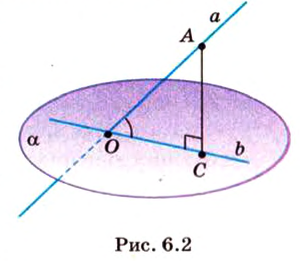
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 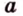
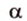
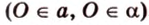
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 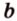
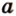
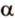
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 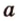
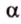
Угол между прямой 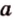
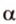
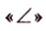
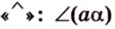
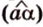
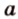
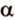
Угол между двумя плоскостями, пространства
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
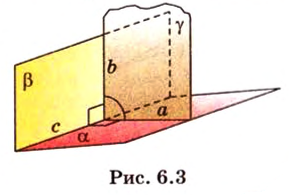
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например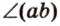
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
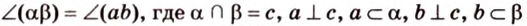
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
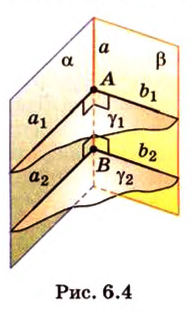
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Доказательство:
Выберем точки 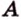
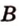
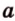
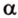
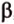
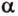
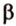
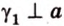
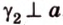
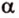
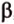
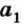
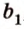
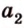
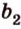
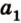
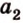
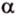
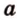
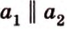
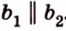
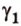
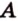
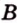
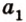
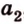
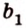
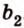
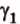
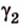
Пример №1
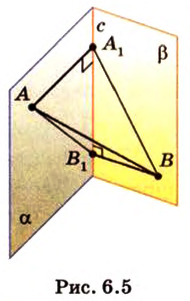
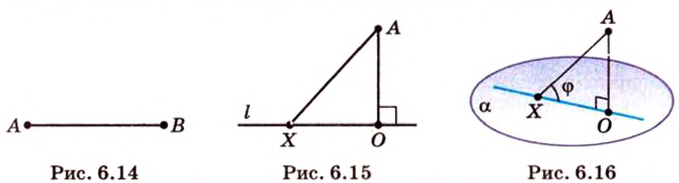
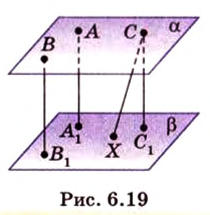
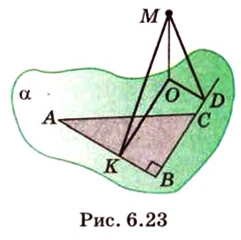
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 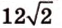
Дано: 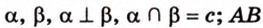

Найти: углы, образованные отрезком 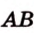
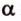
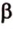
Решение:
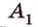
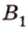
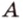
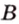
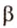
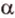
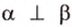
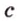
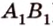
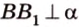
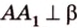
Итак, 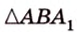
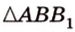
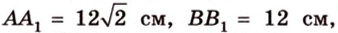
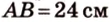
Из 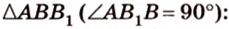
Из 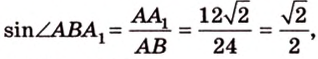
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 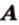
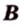
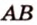
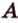
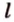
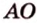
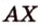
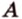
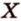
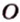
Рассмотрим плоскость 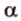
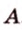
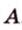
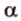
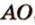
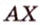
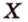
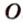
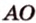
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 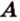
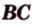
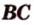
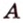
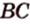
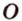
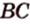
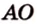
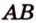

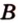
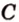
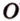
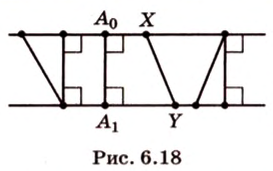
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 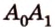
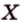
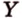
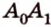
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Доказательство:
Пусть имеем две параллельные плоскости 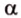
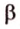
и второй, то перпендикуляр 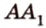
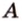
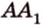
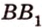
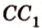
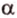
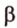
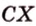
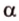
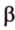
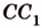
А это вытекает из того, что перпендикуляр 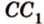
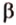
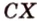
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
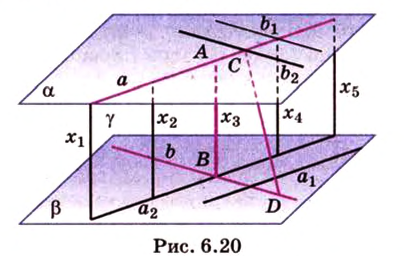
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Доказательство:
Действительно, пусть 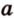
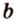
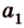
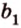
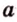
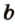
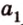
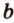
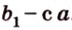
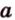
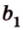
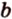
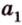
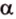
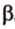
Плоскости 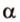
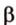
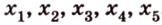
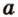
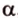
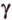
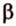
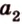
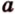
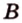
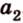
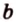
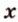
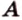
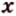
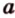
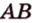
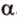
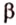
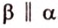
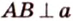
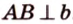
Отрезок 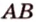
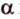
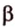
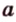
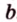
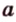
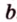
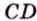
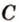
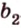
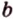

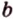
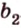
Поскольку она перпендикулярна прямым 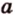
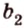

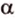




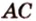
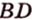
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Пример №2
Отрезок 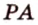
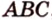
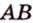
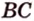
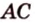
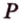
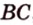
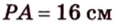
Решение:
Пусть 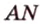
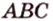
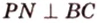
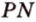
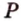
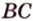
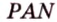
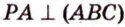
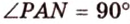
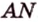
Из формулы для площади треугольника 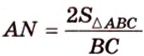
Необходимую площадь определим по формуле Герона:
Тогда 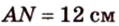
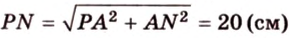
Ответ. 20 см.
Пример №3
Прямая 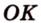
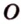
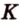
Доказательство:
Пусть 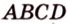
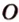
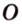
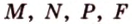
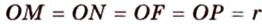
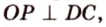
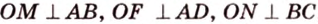
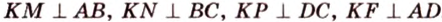
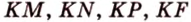
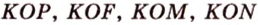
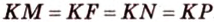
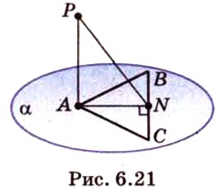
Пример №4
Точка 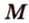
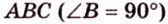
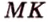
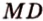
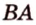
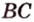
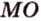
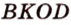
Доказательство:
Поскольку отрезки 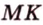
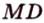
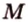
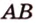
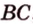
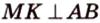
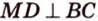
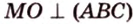
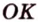
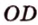
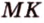
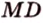
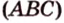
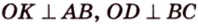
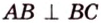
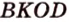
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
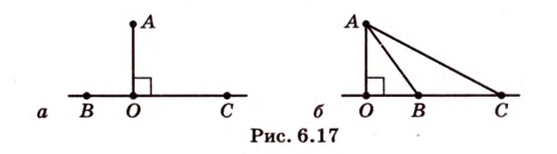
Найди разность углов ABF CBT, стороны треугольников -очевидны.Длины гипотенуз при желании можно вычислить из теоремы Пифагора (в прямоуг.треуг квадрат гипотен =сумме кв. катетов.
Во втором случае рассмотри один из треугольников ,длины его сторон известны,высота треугольника дает ответ об угле против которого она лежит (или угол при вершине (см. как в прямоуг. треуг .связаны стороны и синусы/косинусы/тангенсы острых углов …..сама не помню уже).














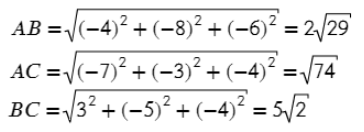
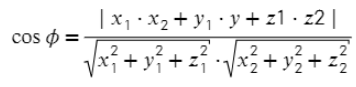
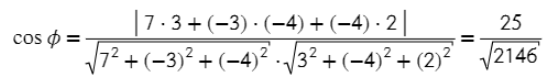
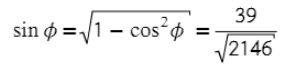
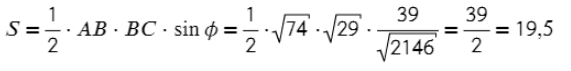
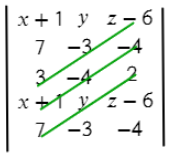
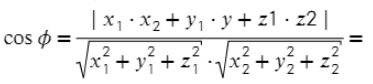
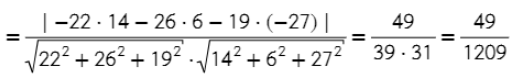
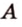 прямой
прямой 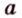
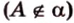 ;
;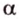
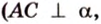
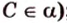 ;
;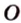 и
и 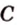 прямую
прямую  .
.