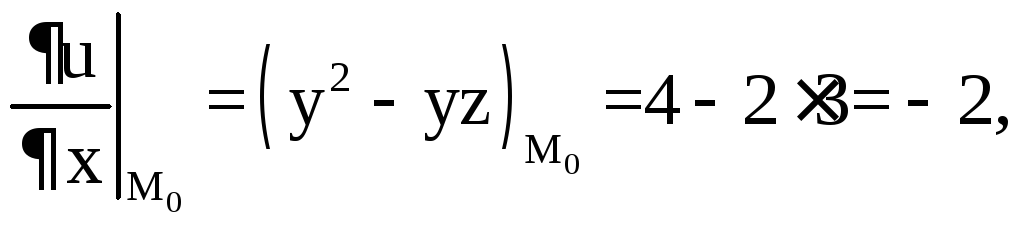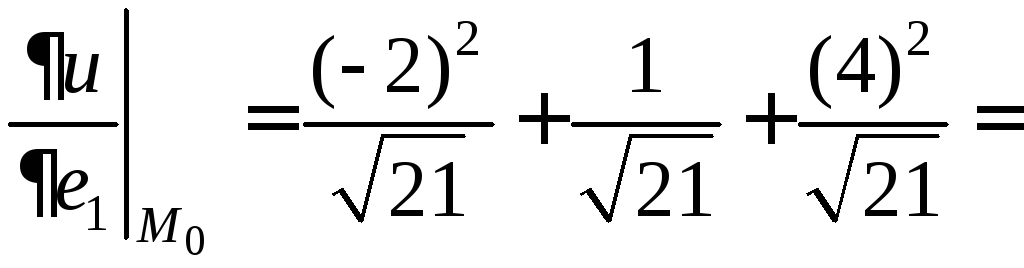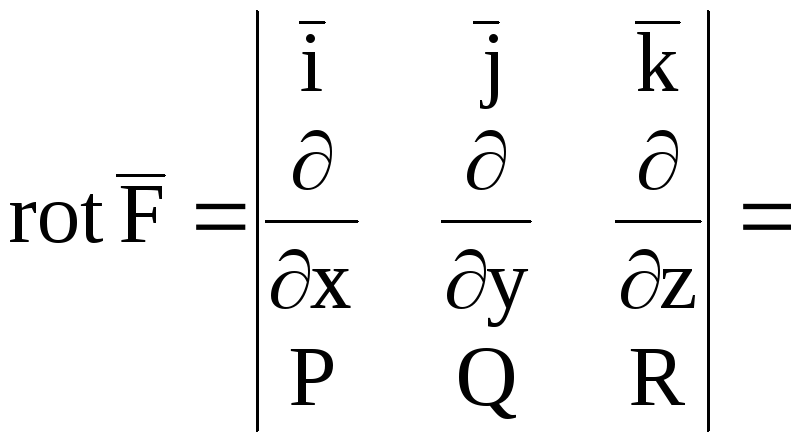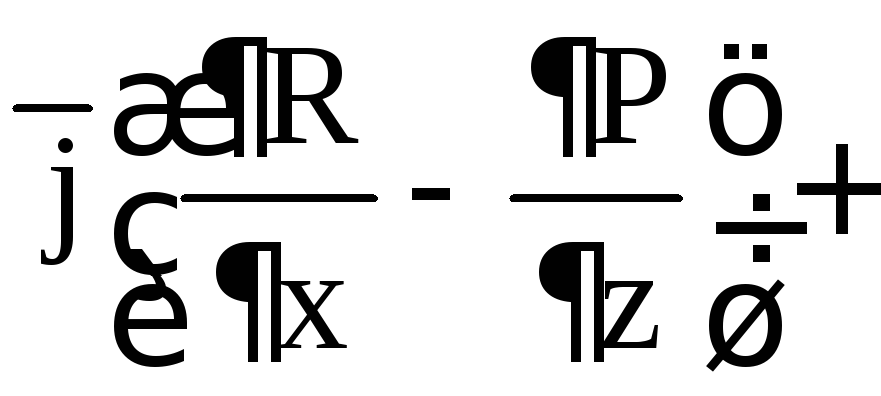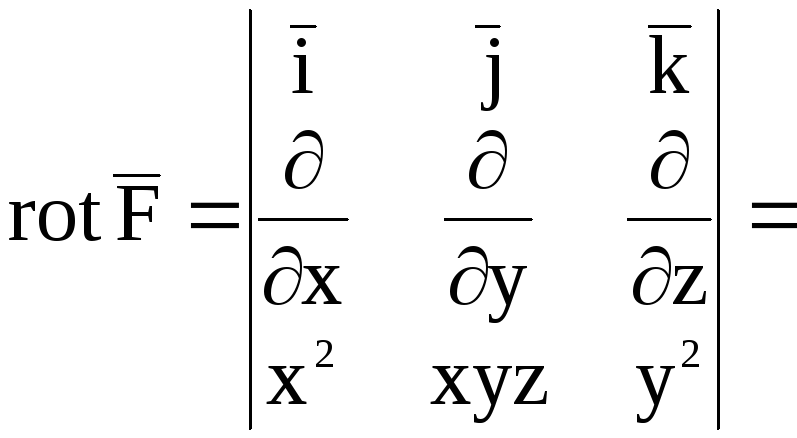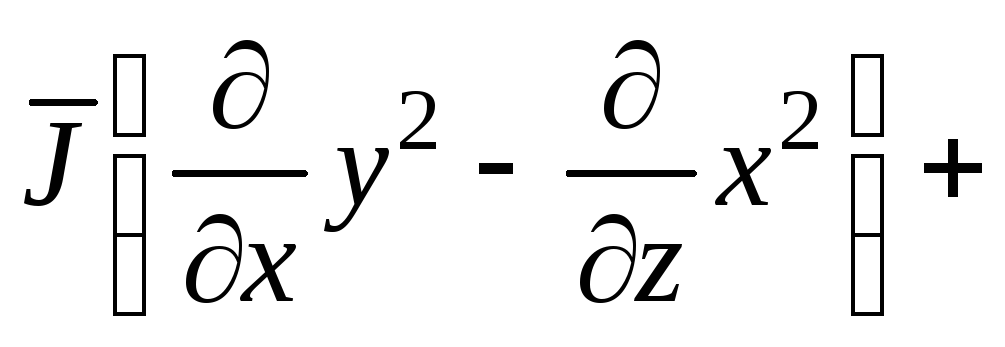Как найти угол между градиентами функции в точках
        Вариант 1     Вариант 2     Вариант 3     Вариант 4     Вариант 5     Вариант 6
        Вариант 7     Вариант 8     Вариант 9     Вариант 10     Вариант 11     Вариант 12
    Вариант 13     Вариант 14     Вариант 15     Вариант 16     Вариант 17     Вариант 18
    Вариант 19     Вариант 20     Вариант 21     Вариант 22     Вариант 23     Вариант 24
    Вариант 25     Вариант 26     Вариант 27     Вариант 28     Вариант 29     Вариант 30
        2.29 Найти угол между градиентами скалярных полей U(x,y,z) и V(x,y,z) в точке M.
Задачка по математике
Найти угол между градиентами в двух точках.
функция z=arcsin(x/(x+y))
Точки: (1,1) и (3,4).
Проверьте пожалуйста решение. В нем явно есть ошибка. Или предложите другой ход решения.
Частные производные и градиенты получились такие:
Повторно перерешал и нашел частные производные. Сам ошибок не нашел — примелькались уже. Вот подробный ход решения:
Высшая математика и экономика
Задача 1.
Найти производную скалярного поля 



Задача 2.
Найти угол между градиентами скалярных полей 

— искомый угол.
Найдём градиент скалярного поля [math]U[/math] в точке [math]M[/math] и модуль:
[math]mathbf{grad}U=frac{partial{U}}{partial{x}},mathbf{i}+frac{partial{U}}{partial{y}},mathbf{j}+frac{partial{U}}{partial{y}},mathbf{k}=frac{3}{2}x^2,mathbf{i}+18y^2,mathbf{j}+9sqrt{6},z^2,mathbf{k}[/math]
[math]left.{mathbf{grad}U}right|_M=frac{3}{2}{!left(sqrt2right)!}^2,mathbf{i}+18{!left(frac{1}{sqrt2}right)!}^2,mathbf{j}+9sqrt6{left(frac{1}{sqrt3}right)!}^2,mathbf{k}=3,mathbf{i}+9,mathbf{j}+3sqrt6,mathbf{k}[/math]
[math]left|left.{mathbf{grad}U}right|_Mright|=sqrt{3^2+9^2+{!left({3sqrt6}right)!}^2}=sqrt{9+81+54}=sqrt{144}=12[/math]
Найдём градиент скалярного поля [math]V[/math] в точке [math]M[/math] и модуль:
[math]mathbf{grad}V=frac{partial{V}}{partial{x}},mathbf{i}+frac{partial{V}}{partial{y}},mathbf{j}+frac{partial{V}}{partial{y}},mathbf{k}=frac{2x}{yz^2},mathbf{i}-frac{x^2}{y^2z^2},mathbf{j}-frac{2x^2}{yz^3},mathbf{k}[/math]
[math]left.{mathbf{grad}V}right|_M=frac{2sqrt2}{frac{1}{sqrt2}left(frac{1}{sqrt3}right)^2},mathbf{i}-frac{left(sqrt2right)^2}{left(frac{1}{sqrt2}right)^2left(frac{1}{sqrt3}right)^2},mathbf{j}-frac{2left(sqrt2right)^2}{frac{1}{sqrt2}left(frac{1}{sqrt3}right)^3},mathbf{k}=12,mathbf{i}-12,mathbf{j}-12sqrt6,mathbf{k}[/math]
[math]left|left.{mathbf{grad}V}right|_Mright|=sqrt{12^2+{!left(-12right)!}^2+{!left(-12sqrt6right)!}^2}=sqrt{12^2cdot8}=24sqrt2[/math]
Вычислим скалярное произведение градиентов полей [math]U[/math] и [math]V[/math] в точке [math]M[/math]
[math]leftlangle{left.{mathbf{grad}U}right|_M,,left.{mathbf{grad}V}right|_M}rightrangle=3cdot12+9cdot(-12)+3sqrt6cdotleft(-12sqrt6right)=36-108-216=-288[/math]
Вычислим значение косинуса угла между градиентами
[math]cosalpha=frac{leftlangle{left.{mathbf{grad}U}right|_M,,left.{mathbf{grad}V}right|_M}rightrangle}{left|left.{mathbf{grad}U}right|_Mright|cdotleft|left.{mathbf{grad}V}right|_Mright|}=frac{-288}{12cdot24sqrt2}=-frac{1}{sqrt2}[/math]
Следовательно, искомый угол [math]alpha[/math] есть
[math]alpha=arccos!left(-frac{1}{sqrt2}right)=pi-arccosfrac{1}{sqrt2}=pi-frac{pi}{4}=frac{3pi}{4}=135^circ[/math]
Также смотрите ещё примеры
viewtopic.php?f=35&t=313
viewtopic.php?f=35&t=3289
Если
каждой точке М некоторой области
пространства поставлено в соответствие
число (скаляр)
,
то говорят, что задано скалярное поле.
В прямоугольной системе координат,
скалярное поле
станет функцией трех переменных
.
Пример скалярных
полей дает поле температур, потенциал
электромагнитного поля и т.д.
Пусть
−
единичный
вектор. Он задает некоторое направление.
Определение.
Производной
от функции
по направлению
называется предел (если он существует)
где
вдоль луча, выходящего из т. M0
по направлению вектора
−длина вектора
Пусть
функция, непрерывно дифференцируемая
в точке M0,
Тогда

Определение.
Градиентом
скалярного поля φ называется вектор
. (2)
Свойства градиента:
а)
из формулы (1) следует, что
;
б),
так как
где
угол между векторами
и
;
в)
если
,
то есть направления
и
совпадают, то
.
Отсюда следует,
что направление
характеризуется тем, что производная
по направлениюбудет наибольшей. То есть
– вектор, направленный в сторону
наибольшего возрастания функции φ.
г)
вектор
в каждой точке направлен по нормали к
поверхности уровня
,
проходящей через эту точку в сторону
возрастания поля.
Пример
1. Даны
скалярное поле
точки
,
.
Найти:
1)
градиент поля
в точке M0;
2)
производную функции
в точке M0
по направлению от точки
к точке M1;
3) производную
функции
в точке M0
в направлении градиента функции в этой
точке;
4)
угол между градиентами данной функции
в точках M0
и M1.
Решение. 1) Находим
частные производные функции
и их значения в точкеM0:
По
формуле (2)
находим
2) Найдем
производную скалярного поля
в точке M0(1,2,3)
по направлению, идущему к точке M1(2,4,5).
Это
направление определяется вектором
,
поэтому по формуле (1)
,
где
,
,
,
получим
,
,
,
.
3)
Найдем производную функции
в точке
по направлению
.
Так
как
то направляющие косинусы
,
,
и
.
4)
Найдем угол между градиентами данной
функции в точках
и
.
Находим
частные производные функции
и их значения в точке M1.
,
,
.
Тогда
.
Угол
φ между градиентами
и
находим по формуле
то
есть
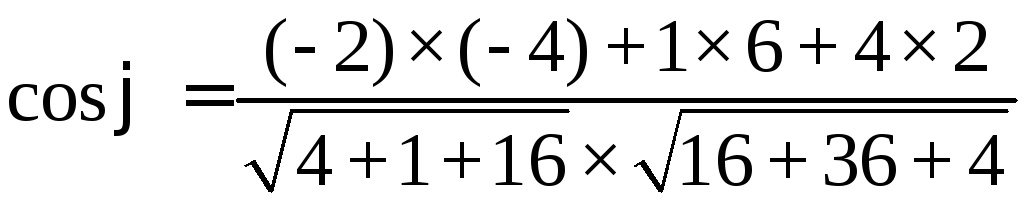
Пример 2.
Найти
производную скалярного поля
в точке M0(1,1),
принадлежащей параболе
по направлению:
1) этой кривой (в
сторону возрастания абсциссы); 2) внешней
нормали к этой кривой.
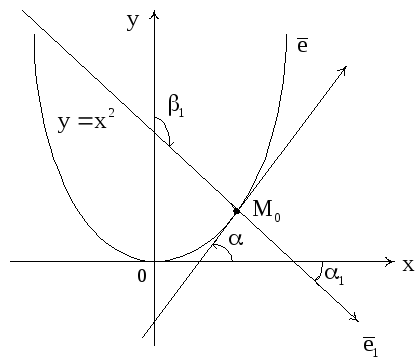
Рис. 2
Решение.
Направлением
параболы
в точке M0(1,1)
считается направление касательной к
параболе в этой точке. Пусть α – угол
наклона касательной к кривой в точке
M0.
Тогда
.
Частные
производные функции
в точке M0:
,
.
По
формуле
получим
.
2)
Пусть
угол наклона внешней нормали к кривой
в точке M0.
Тогда
,
.
.
Пример
3. Для скалярной
функции
найти градиенты в точках P0(1,6)
и P1(0,0),
угол между
и
,
производную по направлению
,
где вектор
перпендикулярен прямой x
– 3y
= 4 и направлен в сторону убывания поля.
Решение.
Вычислим частные производные функции
z
в точках P0
и P1:
;
;
;
.
Тогда
Поскольку
то угол между
и
равен
нулю. Поскольку
то угол между
и
равен нулю.
Найдем
производную по направлению. Так как
вектор
перпендикулярен прямой
то он коллинеарен вектору нормали
этой прямой. Кроме того,
должен быть направлен в сторону убывания
поля. Согласно свойству градиента в
этом случае угол между вектороми
должен быть тупым, а
Вычислим
Поэтому в качестве вектора
возьмем вектор
Вычислим
.
Тогда имеем
.
Определение.
Если в каждой
точке M
некоторой области G
трехмерного пространства задан вектор,
то говорят, что задано векторное поле
.
В
декартовой системе координат задание
поля
(3)
эквивалентно
заданию трех скалярных функций P,
Q,
R.
Примеры:
электростатическое поле, магнитостатическое
поле и т.д. Для векторного поля (3), где
P,
Q,
R
– непрерывные функции своих аргументов,
имеющие непрерывные частные производные
первого порядка, можно ввести две
операции: дивергенцию и ротор.
Определение.
Дивергенцией
векторного поля
называется скалярная функция
. (4)
Ротором
(вихрем)
векторного
поля
называется векторное поле
.
(5)
Замечание.
Данные определения
зависят от системы координат. Ниже (§7,
п.3) даны определения,
,
инвариантные относительно системы
координат.
Пример
4. Найти
дивергенцию векторного поля
.
Решение.
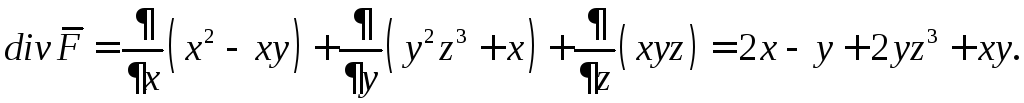
5. Найти ротор
векторного поля
.
Решение.
.
Если
во всех точках M
области
G
,
(6)
то говорят, что
поле соленоидально в этой области.
Задача 62132 Найти угол между градиентами функций u…
Условие
Найти угол между градиентами функций u (x, y, z) и v (x, y, z) в точке М

математика ВУЗ
1178
Решение
★
[m]vec{grad u}=frac{ ∂u }{ ∂x }vec{i}+frac{ ∂u }{ ∂y }vec{j}+frac{ ∂u }{ ∂z }vec{k}[/m]
Находим
[m]frac{ ∂u }{ ∂x }=(frac{z^3}{xy^2})`_{x}=frac{z^3}{y^2}cdot( (x^{-1})`=frac{z^3}{y^2} (-x^{-2})=-frac{z^3}{x^2y^2}[/m]
[m]frac{ ∂u }{ ∂y }=(frac{z^3}{xy^2})`_{y}=frac{z^3}{x}cdot(y^{-2})`=frac{z^3}{x}cdot (-2y^{-3})=-frac{2z^3}{xy^3}[/m]
[m]frac{ ∂u }{ ∂z }=(frac{z^3}{xy^2})`_{z}=frac{1}{xy^2}cdot (z^3)`=frac{1}{xy^2}cdot 3z^2=frac{3z^2}{xy^2}[/m]
[m]vec{grad u}|_{M}=frac{ ∂u }{ ∂x }|_{M}vec{i}+frac{ ∂u }{ ∂y }|_{M}vec{j}+frac{ ∂u }{ ∂z }|_{M}vec{k}[/m]
[m]frac{ ∂u }{ ∂x }|_{M}=-frac{(sqrt{frac{3}{2}})^3}{(frac{1}{3})^2cdot 2^2}=-frac{27sqrt{3}}{8sqrt{2}}[/m]
[m]frac{ ∂u }{ ∂y }|_{M}=-frac{2(sqrt{frac{3}{2}})^3}{frac{1}{3}cdot 2^3}=frac{9sqrt{3}}{8sqrt{2}}[/m]
[m]frac{ ∂u }{ ∂z }|_{M}=frac{3(sqrt{frac{3}{2}})^2}{frac{1}{3}cdot 2^2}=frac{27}{8}[/m]
[red][m]vec{grad u}|_{M}=-frac{27sqrt{3}}{8sqrt{2}}vec{i}+frac{9sqrt{3}}{8sqrt{2}}vec{j}+frac{27}{8}vec{k}[/m][/red]
Аналогично
[m]vec{grad v}=frac{ ∂v }{ ∂x }vec{i}+frac{ ∂v }{ ∂y }vec{j}+frac{ ∂v }{ ∂z }vec{k}[/m]
Находим
[m]frac{ ∂v }{ ∂x }=(9sqrt{2}x^3-frac{y^3}{2sqrt{2}}-frac{4z^3}{sqrt{3}})`_{x}=9sqrt{2}cdot 3x^2=27sqrt{2}x^2[/m]
[m]frac{ ∂v }{ ∂y }=(9sqrt{2}x^3-frac{y^3}{2sqrt{2}}-frac{4z^3}{sqrt{3}})`_{y}=-frac{1}{2sqrt{2}}cdot 3y^2=-frac{3y^2}{2sqrt{2}}[/m]
[m]frac{ ∂v }{ ∂z }=(9sqrt{2}x^3-frac{y^3}{2sqrt{2}}-frac{4z^3}{sqrt{3}})`_{z}=-frac{4}{sqrt{3}}cdot 3z^2=-frac{12}{sqrt{3}}z^2[/m]
[m]vec{grad v}|_{M}=frac{ ∂v }{ ∂x }|_{M}vec{i}+frac{ ∂v }{ ∂y }|_{M}vec{j}+frac{ ∂v }{ ∂z }|_{M}vec{k}[/m]
[m]frac{ ∂v }{ ∂x }|_{M}=27sqrt{2}(frac{1}{3})^2=3sqrt{2}[/m]
[m]frac{ ∂v }{ ∂y }|_{M}=-frac{3}{2sqrt{2}}cdot 2^2=-3sqrt{2}[/m]
[m]frac{ ∂v }{ ∂z }|_{M}=-frac{12}{sqrt{3}}cdot (sqrt{frac{3}{2}})^2=-6sqrt{3}[/m]
[red][m]vec{grad v}|_{M}=3sqrt{2}vec{i}-3sqrt{2}vec{j}-6sqrt{3}vec{k}[/m][/red]
Находим угол между векторами
[red][m]vec{grad u}|_{M}=-frac{27sqrt{3}}{8sqrt{2}}vec{i}+frac{9sqrt{3}}{8sqrt{2}}vec{j}+frac{27}{8}vec{k}[/m][/red]
[red][m]vec{grad v}|_{M}=3sqrt{2}vec{i}-3sqrt{2}vec{j}-6sqrt{3}vec{k}[/m][/red]
по формуле: