Как найти угол между кривыми в точке

Углом
между двумя кривыми
у
= f₁(x)
и у
= f₂(x)
в точке их пересечения М₀(х₀,
у₀)
называется угол между касательными к
этим кривым в точке М₀.
Этот угол определяется по формуле

=

.

Пример.
Найти угол между параболами

у
= 8 – х²
и у
= х².

□ Для
нахождения координат точек пересечения
заданных кривых решим систему уравнений

В
результате получим А(2;
4) и В(−2;
4). Продифференцируем уравнения парабол:

= −2х,

= 2х.
Найдем значения

и

для точки А(2;
4):

= −4,

= 4. Следовательно,

=

=

и

=


.

Аналогично
определяется угол между кривыми в точке
В(−2;
4):

=

.
■

§ 21. Формула тейлора

Теорема.
Пусть функция f(x)
имеет в точке а
и некоторой ее окрестности производные
порядка п
+ 1. Пусть х
– любое значение аргумента из указанной
окрестности, х
≠ а.
Тогда между точками а
и х
найдется точка

такая, что справедлива формула:

f(x)
= f(а)
+

(х
– а)
+
(х
– а)²+
…+

(х
– а)^п
+

+
(х
– а)^п+1.

Эту
формулу называют формулой
Тейлора.

Выражение

R_n+1(x)
=

(х
– а)^п+1

называют
остаточным
членом

формулы Тейлора.

Запишем остаточный
член в другом виде:

так
как

(а,
х),
то найдется число

,
0 <

< 1, что

= а
+

(х
– а)
и тогда

R_n+1(x)
=

(х
– а)^п+1,
0 <

< 1.

Эта
форма остаточного члена наиболее
употребительна в приложениях.

Если
в формуле Тейлора а
= 0, то получим формулу
Маклорена:

f(x)
= f(0)
+

х
+

х²
+
… +

х^п
+
R_n+1(x)

с
остаточным членом

R_n+1(x)
=

х^п+1,
0 <

< 1.

Разложение
некоторых элементарных функций по
формуле Маклорена

1.
f(x)
= е^х.

Так как

f(x)
=

=

= … = f
^п+1(x)
= е^х,

f(0)
=

=

= … = f
^п+1(0)
= 1,

то
формула Маклорена имеет вид

е^х
= 1 +

+

+

+…+

+ R_n+1(x),

где

R_n+1(x)
=

х^п+1,
0 <

< 1.

Аналогично
можно разложить по формуле Маклорена
следующие функции:

2.
f(x)
=

.

= х
−

+

−

+
…+ (−1)^т+1

+ R_2т(x),

где
R_2т(x)
= (−1)^т
·
,
0 <

< 1.

3.
f(x)
=

.

= 1
−

+

−

+
…+ (−1)^т

+ R_2т+1(x),

где
R_2т+1(x)
= (−1)^т+1
·
,
0 <

< 1.

4.
f(x)
= (1 + х)^т.

(1
+ х)^т
=1+
х+
х²+

х³+…+

+

х^п
+R_n+1(x),

где

R_n+1(x)=

х^п+1(1
+

)^т—п-1,
0 <

< 1.

Пример.
Вычислить число е.

□ Запишем
разложение е^х
по формуле Маклорена:

е^х

= 1+

+

+

+…+

+
х^п+1,
0 <

< 1.

Если
заменить функцию е^х
ее многочленом Тейлора степени п
(отбросим остаточный член), то получим
приближенное равенство

е^х

1 +

+

+

+…+

,
(1)

абсолютная
погрешность которого

| R_n+1(x)
| =

| х
|^п+1,
0 <

< 1.

Если
рассматривать функцию е^х
для −1 ≤ х
≤ 1, то

|
R_n+1(x)
| ≤

<

.

Полагая
в (1) х
= 1, получаем приближенное значение числа

е
≈ 1+

+

+

+ …+

.

При
этом | R_n+1(x)
| <

.

Если
требуется вычислить значение е
с точностью

= 0,001, то число п
определяется из неравенства

< 0,001, или (п
+ 1)! > 3000,

которое
выполняется при п
= 6. Следовательно,

е
≈ 1+

+

+

+ …+

.

Вычисляя
с четырьмя знаками после запятой, получим

е
≈ 2,7180.

Три
знака после запятой гарантированы.
■

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Задание. Найти тангенс угла между кривыми $y=x^2-1$ и
$y=x^3-1$ в точке их пересечения, которая имеет большую абсциссу.

Решение. Вначале найдем точки пересечения графиков заданных функций, для этого совместно разрешим уравнение заданных кривых:

$$begin{array}{c}
left{begin{array}{l}
y_{1}=x^{2}-1 \
y_{2}=x^{3}-1
end{array} Rightarrow x^{2}-1=x^{3}-1 Rightarrow x^{3}-x^{2}=0 Rightarrowright. \
Rightarrow x_{1,2}=0, x_{3}=1
end{array}$$

Таким образом, искомая точка $x=1$.

Далее находим производные заданных функций в найденной точке:

$$begin{array}{c}
y_{1}^{prime}=left(x^{2}-1right)^{prime}=left(x^{2}right)^{prime}-(1)^{prime}=2 x-0=2 x, y_{1}^{prime}(1)=2 \
y_{2}^{prime}=left(x^{3}-1right)^{prime}=left(x^{3}right)^{prime}-(1)^{prime}=3 x^{2}-0=3 x^{2}, y_{2}^{prime}(1)=3
end{array}$$

Итак, искомый тангенс:

$$operatorname{tg} phi=frac{3-2}{1+2 cdot 3}=frac{1}{7}$$

Ответ. $operatorname{tg} phi=frac{1}{7}$

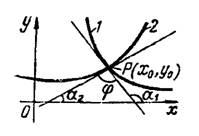
Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 1) по формуле

где и — угловые коэффициенты касательных к кривым в точке их пересечения ,
т. е. частные значения в точке производных от по из уравнений этих кривых:

Рис.1

Пример 1. Найти углы, под которыми пересекаются следующие линии:
1) прямая и парабола ;
2) эллипс и парабола ;
3) синусоида и косинусоида .
Решение.
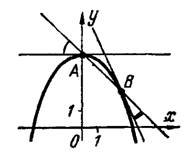
1) Совместно решая уравнения параболы и прямой, находим, что они пересекаются в двух точках: и , рис.2.

Рис.2

Далее находим производную от по из уравнения параболы: и определяем угловые коэффициенты касательных к параболе в точках и , как частные значения этой производной:

Угловой коэффициент прямой один и тот же во всех ее точках; у данной прямой он равен — 1.
Согласно формуле (2) получим

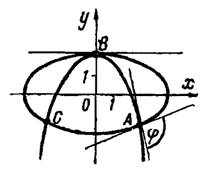
2) Решая совместно уравнения кривых, находим их общие точки: и рис.3. Затем определяем угловые коэффициенты и касательных в любой точке эллипса и параболы как производные от по из их уравнений

Рис.3

Подставляя координаты точки , получим и . Следовательно, в точке :

Под таким же углом кривые пересекаются и в точке вследствие их симметричности относительно оси .
В точке имеем: , следовательно, в точке кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.
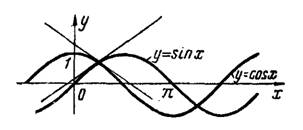
3) Абсциссы точек пересечения кривых (рис.4) определяются уравнением , решая которое, получим

Дифференцированием находим угловые коэффициенты касательных к синусоиде и косинусоиде:

Рис.4

Искомый угол между кривыми определяем по общей формуле (2)

Положительному знаку соответствует острый угол , отрицательному — тупой, смежный с ним угол .

How to Find Angle Between Two Curves — Formula, Example

Геометрическое применение производной

Наталья Игоревна Восковская

Эксперт по предмету «Математика»

Задать вопрос автору статьи

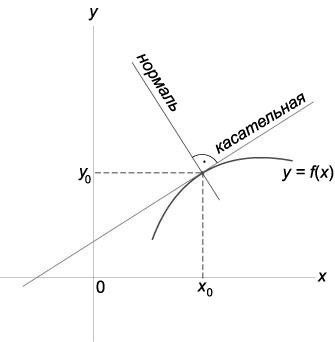
Что такое касательная и нормаль к кривой

Определение

Касательная — прямая которая совпадает и проходит через точку кривой с точностью до первого порядка.

Рисунок 1. Нормаль и касательная к кривой

Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):

[y-y_{0} =y`(x_{0} )(x-x_{0} )]

Для кривой вида y = f(x) уравнение касательной в точке М(x0,y0):

[y-y_{0} =-frac{1}{y`(x_{0} )} (x-x_{0} )]

Пример 1

Написать уравнение касательной и нормали к кривой в точке с абсциссой $x_0=1$:

[y=3x^{2} -2x+11]

Решение.

1. Найдем значение функции в точке:

[y_{0} =3cdot 1^{2} -2cdot 1+11=12]

2. Найдем производную в данной точке:

[y'(x_{0} )=left(3x^{2} -2x+11right){{‘} } =6x-2]

[y'(1)=6cdot 1-2=4]

3. Запишем уравнение касательной:

[y-y_{0} =y`(x_{0} )(x-x_{0} )]

[y-12=4(x-1)]

[y-4x-8=0]

4. Запишем уравнение нормали:

[y-12=-frac{1}{4} (x-1)]

[4y+x-49=0]

Угол между двумя кривыми в точке М(x0,y0) является наименьшим из возможных углов между касательными. Пусть уравнения касательных имеют вид:

$y=f_{1} (x)$ и $y=f_{2} (x)$

$y=k_{1} x+b_{1} $ и $y=k_{2} x+b_{2} $

Тогда тангенс угла между двумя кривыми находится по формуле:

[tggamma =frac{k_{2} -k_{1} }{1+k_{1} k_{2} } =frac{f’_{2} (x_{0} )-f’_{1} (x_{0} )}{1+f’_{1} (x_{0} )f’_{2} (x_{0} )} ]

Пример 2

Найти тангенс угла между кривыми, в точке имеющей большую абсциссу.

[begin{array}{l} {y=2x^{2} -3} \ {y=4x-2} end{array}]

Решение.

1. Для того чтобы определить точки пересечения кривых необходимо решить систему уравнений:

[left{begin{array}{l} {y=2x^{2} -3} \ {y=4x-2} end{array}right. ]

[2x^{2} -3=4x-2]

[2x^{2} -4x=1]

[2x(x-2)=1]

Значит, кривые пересекаются в точках 0,5 и 2. Максимальной, из которых, является точка x = 2.

2. Найдем производные в найденной точке

[y_{1} {{‘} } =left(2x^{2} -3right){{‘} } =4x]

[y_{2} {{‘} } =left(4x-2right){{‘} } =4]

[y_{1} {{‘} } =4cdot 2=8]

[y_{2} {{‘} } =4]

3. Запишем уравнение тангенса угла и подставим все известные значения

[tggamma =frac{4-8}{1+8cdot 4} =frac{-4}{33} ]

«Геометрическое применение производной» 👇

Что такое длина касательной и нормали, подкасательная и поднормаль

Определение

Длина отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой называется длиной касательной.

Определение

Проекция отрезка от пересечения касательной оси ОХ до пересечения с нормалью или кривой на ось Ох называется подкасательной (ST).

Определение

Длина отрезка от пересечения нормали с касательной или кривой до точки соприкосновения с осью Ох называется длиной нормали, а проекция отрезка на ось — поднормалью (SN).

Пример 3

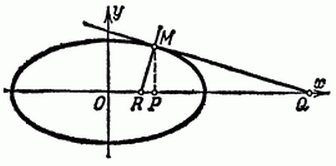
Найти длину подкасательной и поднормали для эллипса x = acost, y = bsint

Рисунок 2. Эллипс

Решение.

1. Уравнение касательной имеет вид:

[y-frac{b}{sqrt{2} } =-frac{b}{a} (x-frac{a}{sqrt{2} } )]

2. Уравнение нормали имеет вид:

[y-frac{b}{sqrt{2} } =frac{a}{b} (x-frac{a}{sqrt{2} } )]

3. Длины подкасательной и поднормали:

[S_{T} =left|frac{frac{b}{sqrt{2} } }{-frac{b}{a} } right|=frac{a}{sqrt{2} } ]

[S_{N} =left|frac{b}{sqrt{2} } left(-frac{b}{a} right)right|=frac{b^{2} }{asqrt{2} } ]

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 15.12.2022