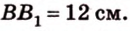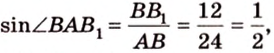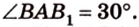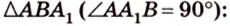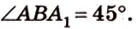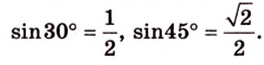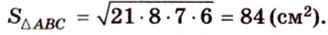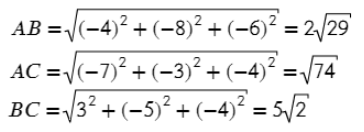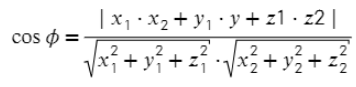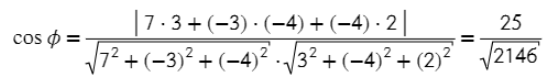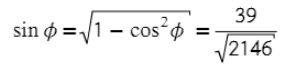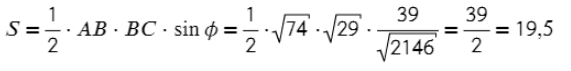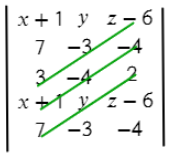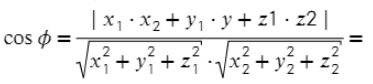Содержание:
В планиметрии угол — это геометрическая фигура, образованная двумя лучами, которые выходят из одной точки — вершины угла (лучи — стороны угла). Такое определение понятия угла переносится и в стереометрию. Углы в пространстве рассматриваются между двумя прямыми, прямой и плоскостью, двумя плоскостями. Опишем и определим каждый из этих случаев.
Угол между двумя прямыми в пространстве
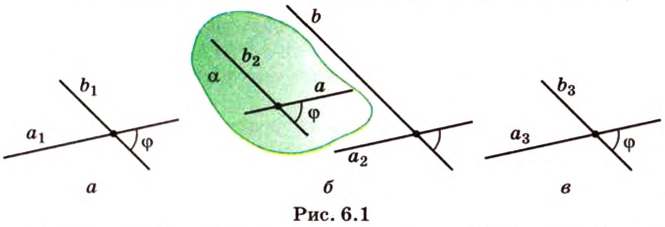
Две прямые, лежащие в одной плоскости, при пересечении образуют смежные и вертикальные углы. В модуле 1 мы повторили все свойства таких углов (вертикальные углы равны, а смежные — дополняют друг друга до 180°). В пространстве (аналогично планиметрии) также сохраняются все названия и понятия об углах и их величинах. Меньший из углов, образованных двумя пересекающимися прямыми, называют углом между прямыми. Угол между перпендикулярными прямыми равен 90°. Считают, что параллельные прямые также образуют угол, равный 0°. В стереометрии рассматривают угол между скрещивающимися прямыми. Пусть даны скрещивающиеся прямые
Углом между скрещивающимися прямыми называется угол между прямыми, которые пересекаются и соответственно параллельны скрещивающимся. 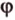
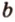
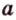
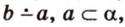
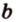
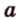
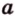
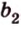
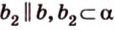
Итак,
Если 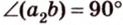
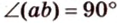
Угол между прямой и плоскостью в пространстве
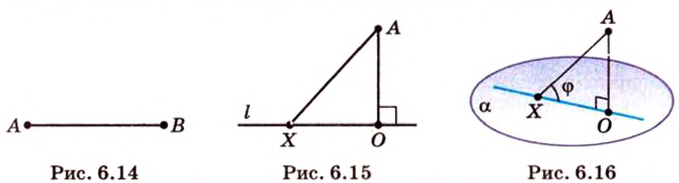
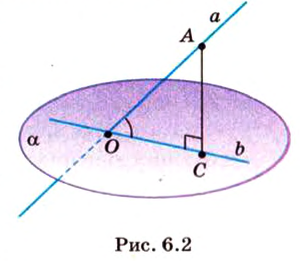
Об угле наклона прямой к плоскости говорят в том случае, когда прямая пересекает эту плоскость. Чтобы построить, например, угол между прямой 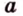
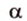
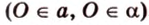
- выбирают точку
прямой
;
- проводят из точки
перпендикуляр к плоскости
;
- проводят через точки плоскости
и
прямую
.
Прямую 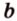
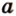
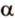
Углом между прямой и плоскостью называется угол между этой прямой и ее проекцией на плоскость. Если прямая 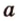
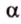
Угол между прямой 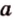
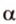
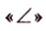
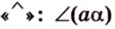
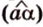
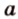
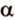
Угол между двумя плоскостями, пространства
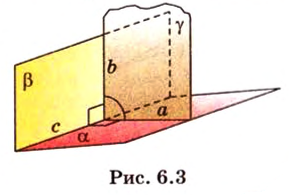
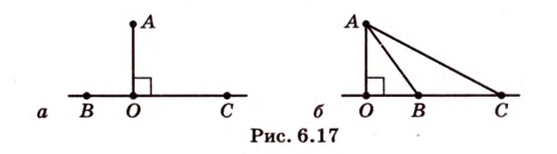
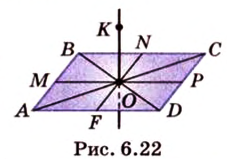
Прямая на плоскости разбивает ее на две полуплоскости. Две полуплоскости могут иметь общую прямую и не образовывать одну плоскость. В этом случае они образуют фигуру, которую называют двугранным углом.
Двугранным углом называется фигура, образованная двумя полуплоскостями вместе с общей прямой, их ограничивающей. Эту прямую называют ребром двугранного угла.
Если двугранный угол пересечь плоскостью, перпендикулярной его ребру, то лучи, по которым она пересекает заданные
полуплоскости, образуют линейный угол, например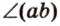
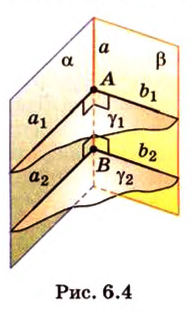
Пересекающиеся плоскости образуют четыре угла. Чтобы определить угол между двумя плоскостями, проводят плоскость, перпендикулярную прямой их пересечения. Она пересекает данные плоскости по двум прямым. Угол между этими прямыми называется углом между данными плоскостями. Т.е. угол между двумя пересекающимися плоскостями — это угол между двумя прямыми, которые принадлежат этим плоскостям и перпендикулярны прямой их пересечения.
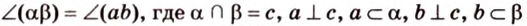
Если линейный угол — 90°, то плоскости перпендикулярны. Если плоскости параллельны, то угол между ними равен 0°.
Теорема 1
Угол между плоскостями не зависит от места построения линейного угла.
Доказательство:
Выберем точки 
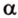
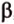
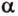
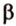
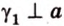
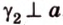
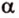
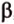
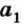
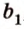
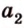
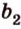
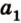
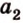
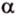
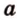
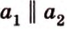
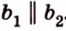
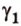
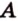
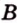
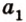
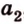
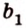
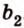
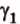
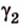
Пример №1
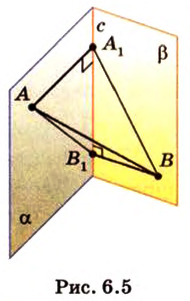
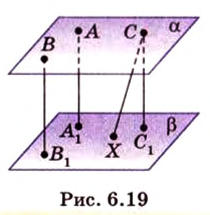
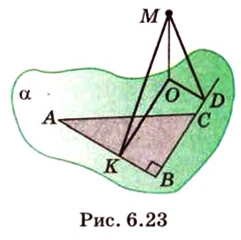
Концы отрезка длиной 24 см принадлежат двум перпендикулярным плоскостям. Расстояния от концов отрезка до линии пересечения данных плоскостей равны 12 см и 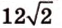
Дано: 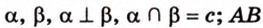

Найти: углы, образованные отрезком 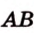
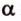
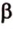
Решение:
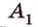
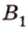
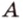
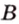
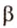
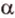
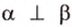
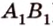
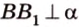
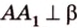
Итак, 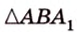
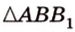
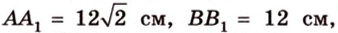
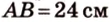
Из 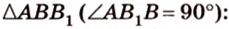
Из 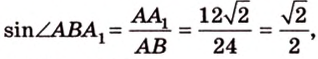
Ответ. 30°; 45°.
Почему именно так?
В этой задаче важно построить проекции концов отрезка на другую, перпендикулярную ей, плоскость. При этом следует помнить, что они должны лежать на прямой пересечения данных перпендикулярных плоскостей, согласно свойствам перпендикулярных плоскостей. Далее, рассматривая прямоугольные треугольники, нужно правильно использовать определение синуса угла как отношения противолежащего катета к гипотенузе и таблицу значений:
Расстояния в пространстве
Одним из ключевых понятий геометрии является длина отрезка. Через него вводится много других понятий, связанных с понятием расстояния. Как известно, расстоянием между двумя точками 
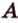
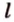
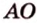
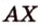
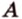
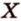
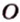
Рассмотрим плоскость 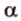
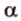
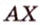
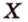
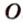
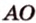
Итак, расстояние от точки до плоскости равно длине перпендикуляра, проведенного из этой точки к плоскости.
Если точка принадлежит плоскости, то в этом случае расстояние от нее до плоскости равно нулю.
Расстояние от точки 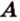
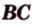
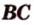
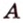
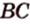
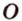
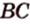
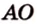
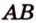

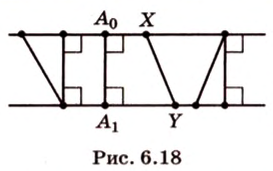
Расстояние между двумя параллельными прямыми равно длине общего перпендикуляра этих прямых (рис. 6.18). Это вытекает из того, что все такие перпендикуляры 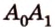
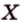
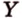
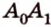
Теорема 2 (о расстоянии между параллельными прямой и плоскостью)
Расстояние между параллельными прямой и плоскостью равно длине общего перпендикуляра, проведенного из произвольной точки прямой к плоскости.
Данная теорема доказывается рассуждениями, аналогичными приведенным выше, о расстоянии между параллельными прямыми.
Теорема 3 (о расстоянии между параллельными плоскостями)
Расстояние между параллельными плоскостями равно длине общего перпендикуляра, проведенного из произвольной точки одной плоскости ко второй.
Доказательство:
Пусть имеем две параллельные плоскости 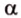
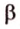
и второй, то перпендикуляр 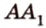
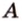
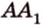
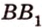
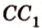
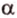
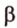
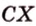
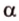
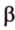
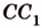
А это вытекает из того, что перпендикуляр 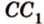
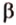
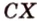
Понятие расстояния между точками широко применяется в разнообразных сферах жизни человека — от науки до быта и досуга. Используется оно в тех случаях, когда размерами реальных объектов, расстояние между которыми вычисляется, в данных условиях можно пренебречь. Так мы говорим о расстоянии между звездами, планетами, передатчиками и принима-телями информации, населенными пунктами, ядрами атома и электронами на его орбите и т.п.
Расстояние между скрещивающимися прямыми
Сначала рассмотрим определение перпендикуляра, проведенного к двум скрещивающимся прямым, и докажем его существование и единственность.
Общим перпендикуляром к двум скрещивающимся прямым называется отрезок с концами на этих прямых, перпендикулярный каждой из них.
Теорема 4
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом только один. Он является общим перпендикуляром к параллельным плоскостям, проходящим через эти прямые.
Доказательство:
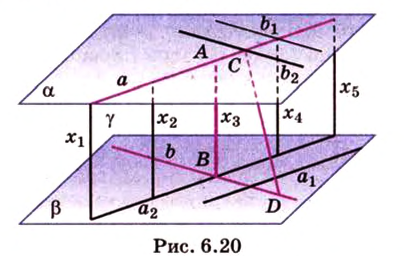
Действительно, пусть 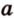
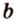
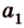
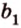
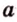
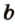
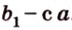
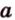
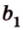
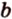
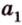
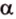
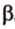
Плоскости 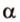
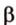
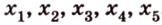
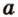
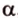
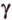
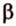
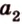
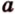
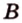
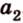
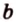
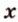
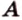
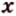
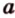
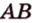
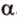
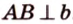
Отрезок 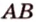
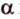
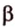
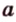
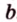
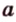
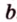
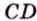
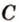
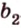
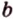

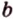
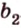
Поскольку она перпендикулярна прямым 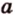
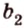

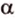




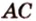
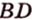
Расстоянием между скрещивающимися прямыми называется длина их общего перпендикуляра.
Пример №2
Отрезок 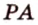
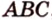
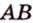
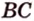
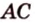
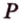
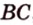
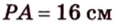
Решение:
Пусть 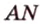
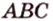
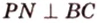
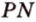
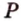
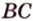
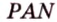
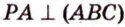
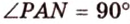
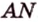
Из формулы для площади треугольника 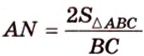
Необходимую площадь определим по формуле Герона:
Тогда 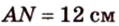
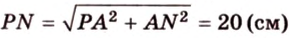
Ответ. 20 см.
Пример №3
Прямая 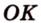
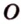
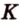
Доказательство:
Пусть 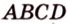
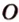
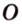
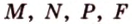
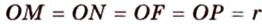
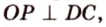
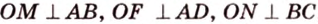
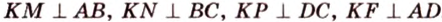
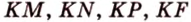
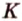
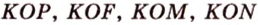
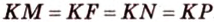
Пример №4
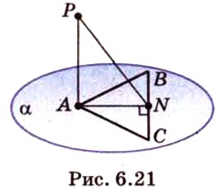
Точка 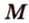
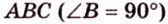
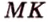
Доказательство:
Поскольку отрезки 
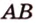
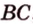
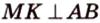
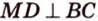
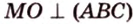
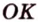
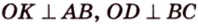
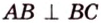
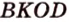
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
- Теорема синусов и теорема косинусов
- Квадрат и его свойства
- Трапеция и ее свойства
- Площадь трапеции
- Центральные и вписанные углы
© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Угол между векторами
Определение
Угол между векторами — это угол между отрезками, которые изображают эти две направляющие и которые отложены от одной точки пространства. Другими словами — это кратчайший путь, на который можно повернуть один из векторов вокруг его начала до положения общей направленности со вторым.
На изображении это α, который также можно обозначить следующим образом:
(left(widehat{overrightarrow a;overrightarrow b}right))
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как и любой другой угол, векторный может быть представлен в нескольких вариациях.
Острый:
Тупой:
Прямой:
С величиной (0^circ) (то есть, векторы сонаправлены):
С величиной (180^circ) (векторы направлены в противоположные стороны):
Нахождение угла между векторами
Как правило, угол между ( overrightarrow a) и (overrightarrow b) можно найти с помощью скалярного произведения или теоремы косинусов для треугольника, который был построен на основе двух этих направляющих.
Определение
Скалярное произведение — это число, которое равно произведению двух направляющих на косинус угла между ними.
Формула скалярного произведения:
(left(overrightarrow a;overrightarrow bright)=left|overrightarrow aright|timesleft|overrightarrow bright|timescosleft(widehat{overrightarrow a;overrightarrow b}right))
- Если α — острый, то СП (скалярное произведение) будет положительным числом (cos острого угла — положительное число).
- Если векторы имеют общую направленность, то есть угол между ними равен (0^circ), а косинус — 1, то СП будет тоже положительным.
- Если α — тупой, то скалярное произведение будет отрицательным (cos тупого угла — отрицательное число).
- Если α равен (180^circ), то есть векторы противоположно направлены, то СП тоже отрицательно, потому что cos данного угла равен 1.
- Если α — прямой, то СП равно 0, так как косинус (90^circ) равен 0.
В случае, если overrightarrow a и overrightarrow b не нулевые, можно найти косинус α между ними, опираясь на формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Расчет угла, если вектор задан координатами
В случае, когда направляющие расположены на двухмерной плоскости с заданными координатами в виде (overrightarrow a=left(a_x;a_yright)) и (overrightarrow b=left(b_x;b_yright)), то угол между ними можно найти следующим образом:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Если же координаты находятся в трехмерном пространстве и заданы в виде:
(overrightarrow a=left(a_x;a_y;a_zright))
( overrightarrow b=left(b_x;b_y;b_zright))
то формула принимает такой вид:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Расчет угла, если заданы три точки в прямоугольной системе координат
В этом случае проще будет разобраться с объяснениями сразу на примере.
Допустим, нам известны три точки и их координаты: A(3,-2), B(2,1), C (6,-1). Нужно найти косинус угла между (overrightarrow{AC}) и (overrightarrow{BC}).
Решение
Для начала найдем их координаты по известным координатам заданных точек:
(overrightarrow{AC}=(6-3, -1-(-2))=(3,1))
(overrightarrow{BC}=(6-2, -1-1)=(4,-2))
После этого уже можем применить формулу для определения косинуса угла на плоскости и подставить известные значения:
(cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac{(overrightarrow{AC};;overrightarrow{BC})}{left|overrightarrow{AC}right|cdotleft|overrightarrow{BC}right|}=frac{3cdot4+1cdot(-2)}{sqrt{3^2+1^2}cdotsqrt{4^2+{(-2)}^2}}=frac{10}{sqrt{10}cdot2sqrt5}=frac{10}{10sqrt2}=frac1{sqrt2})
Ответ: (cosleft(widehat{overrightarrow{AC};overrightarrow{BC}}right)=frac1{sqrt2}.)
Примеры решения задач
Для наглядности, взглянем на примеры решения задач по данной теме.
Задача 1
Известно, что (overrightarrow a) и (overrightarrow b). Их длины равны 3 и 6 соответственно, а скалярное произведение равно -9. Нужно найти cos угла между векторами и его величину.
Решение
Применим формулу:
( cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|})
Подставим известные значения:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{-9}{3cdot6}=-frac12)
Далее найдем угол между данными векторами:
(arccosleft(-frac12right)=frac{3pi}4)
Ответ: (left(widehat{overrightarrow a;overrightarrow b}right)=-frac12,;left(widehat{overrightarrow a;overrightarrow b}right)=frac{3pi}4.)
Задача 2
В пространстве даны координаты (overrightarrow a=(8; -11; 7)) и (overrightarrow b=(-2; -7; 8)). Вычислить угол α между ними.
Решение
Используем формулу для нахождения косинуса угла между направляющими в трехмерной системе координат:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y+a_zcdot b_z}{sqrt{a_x^2+a_y^2+a_z^2}cdotsqrt{b_x^2+b_y^2+b_z^2}})
Подставляем значения и получаем:
(cosleft(alpharight)=frac{8cdot(-2)+(-11)cdot(-7)+7cdot8}{sqrt{8^2+{(-11)}^2+7^2}cdotsqrt{{(-2)}^2+{(-7)}^2+8^2}}=frac{117}{sqrt{234}cdotsqrt{117}}=frac{sqrt{117}}{sqrt{234}}=frac1{sqrt2}=frac2{sqrt2})
Теперь находим угол α:
(alpha=arccosleft(frac2{sqrt2}right)=45^circ)
Ответ: (45^circ).
Задача 3
Известны (overrightarrow a=(3; 4)) и (overrightarrow b=(2; 5)). Найти угол между ними.
Решение
Для расчета используем формулу:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}})
Подставим известные значения и получим:
(cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{left(overrightarrow a;overrightarrow bright)}{left|overrightarrow aright|timesleft|overrightarrow bright|}=frac{a_xcdot b_x+a_ycdot b_y}{sqrt{a_x^2+a_y^2}cdotsqrt{b_x^2+b_y^2}}=frac{3cdot2+4cdot5}{sqrt{3^2+4^2}cdotsqrt{2^2+5^2}}=frac{26}{sqrt{25}cdotsqrt{29}}=frac{26}{5sqrt{29}})
Ответ: (cosleft(widehat{overrightarrow a;overrightarrow b}right)=frac{26}{5sqrt{29}})
Метод координат (углы между векторами и плоскостями)
Нахождение координат и длин вектора.
Вычисление угла между векторами.
Составление уравнение плоскости по трем точкам.
Решение задач с доказательством.
Для того, чтобы успешно решать задачи методом координат, полезно помнить:
Чтобы задать вектор, проходящий черерз 2 точки, нужно из координат второй точки вычесть координаты первой точки.
Чтобы найти длину вектора, нужно извлечь корень квадратный из суммы квадратов его координат.
Задача. Найти координаты и длины векторов AB, BC, AC, если точки имееют координаты А = (5; 8; 3), B = (1; 0; −3), C = (−2; 5; −1).
AB = (1−5; 0-8; −3−3) = (−4; −8; −6)
AC = (−2−5; 5−8; −1−3) = (−7; −3; −4)
BC = (1−(−2); 0−5; −1−3) = (3; −5; −4)
Для нахождения угла между двумя векторами a = (x1; y1; z1) и b = (x2; y2; z2):
Задача. Найдите площадь треугольника, ограниченную точками A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
- Вычисляем косинус угла между векторами.
- Через основное тригометрическое тождество получаем синус.
- Подставляем в формулу площади.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
Задача. Задайте уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
- Находим координаты векторов.
- Задаем матрицу плоскости.
- Вычисляем ее определитель, это и есть уравнение плоскости.
AB = (3−(−4); 1−4; 0−4) = (7; −3; −4)
AC = (−1−(−4); 0−4; 6−4) = (3; −4; 2)
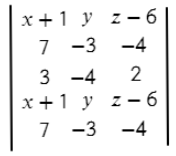
Вторая строчка — координаты первого вектора.
Третья строчка — координаты второго вектора (нет разницы какой из векторов задавать во второй строчке, а какой в третьей).
Четвертая заполняется аналогично первой.
Пятая — аналогично второй.
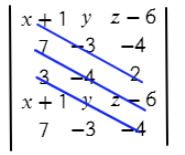
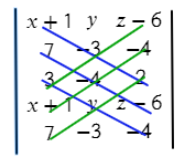
Теперь перемножаем все значения на одном синем отрезке и складываем с другими значениями на других отрезках:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4)
Аналогично делаем с зелеными отрезками:
(z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7
Осталось из значений синих отрезков вычесть значения зеленых отрезков:
(х+1)*(−3)*2 + 7*(−4)*(z−6) + 3*y*(−4) − ((z−6)*(−3)*3 + (−4)*(−4)*(x+1) + 2*y*7) =
= −22х −26y −19z + 92
−22х −26y −19z + 92 — искомое уравнение плоскости, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6).
P.s. Если вам кажется, что это сложно, то огорчу вас. Одна из первых тем (самых простых), которые вы будите проходить на первом курсе любого университета — это матрицы, так что можно немного облегчить себе жизнь и разобраться заранее.
Задача. Найдите угол между плоскостью, проходящей через точки A = (−4; 4; 4), B = (3; 1; 0), C = (−1; 0; 6), и плоскостью, заданную уравнением
14x + 6y −27z + 51 = 0.
- Задаем уравнение плоскости, проходящей через 3 точки ( нашли в предыдущей задаче).
- Находим косинус угла между плоскостями ( формула аналогична косинусу угла между прямыми).
Будь в курсе новых статеек, видео и легкого математического юмора.
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.
Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Сумма векторов:
Разность векторов:
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
:
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
Для точки M:
То есть A + C + D = 0.
Для точки N:
Аналогично для точки K:
Получили систему из трех уравнений:
.
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
;
.
Выразим C и B через A и подставим в третье уравнение:
.
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Упростим систему:
.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Итак, AA1 = √3
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
08.05.2023

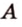 прямой
прямой 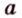
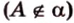 ;
;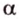
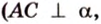
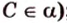 ;
;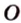 и
и 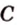 прямую
прямую 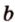 .
.