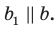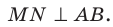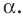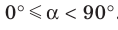Как найти угол между перпендикулярами к плоскостям

На этой странице вы узнаете

• Как мы сталкиваемся с двугранными углами, когда читаем книгу?
• Где в комнате можно найти перпендикулярные плоскости?
• Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?

Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться. 

Углы между плоскостями

Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели. 

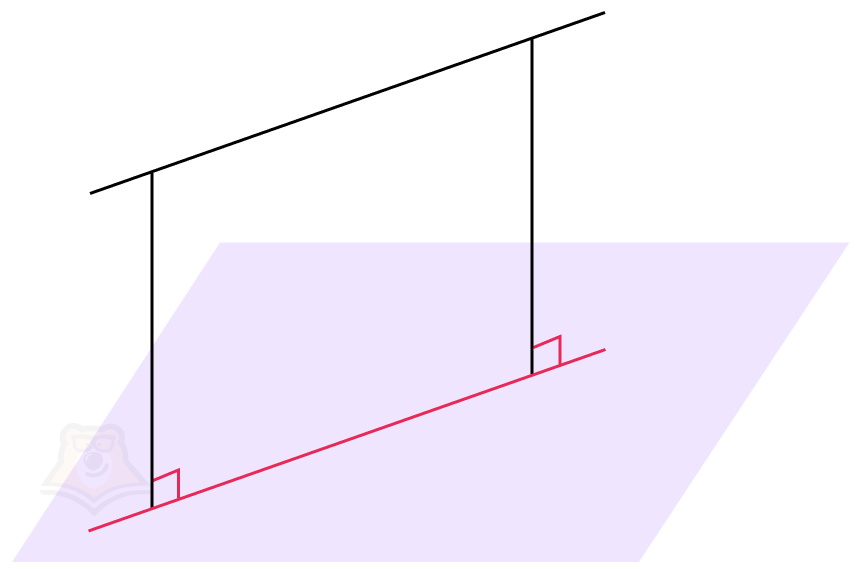
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия. 

Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла. 

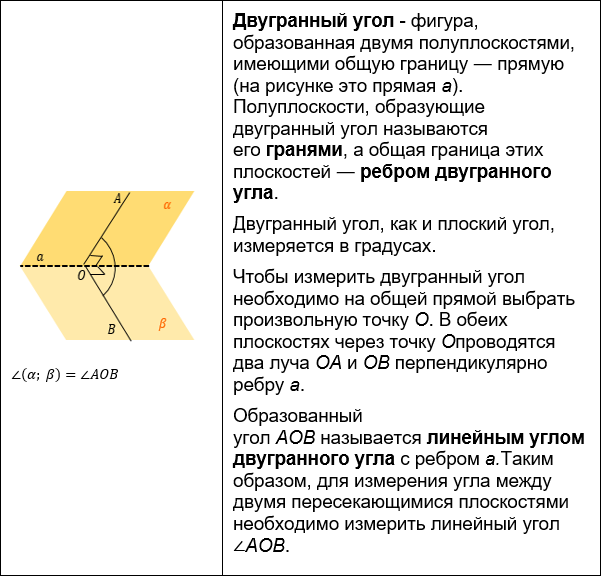
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. 

Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке: 
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b  — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.  

Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.

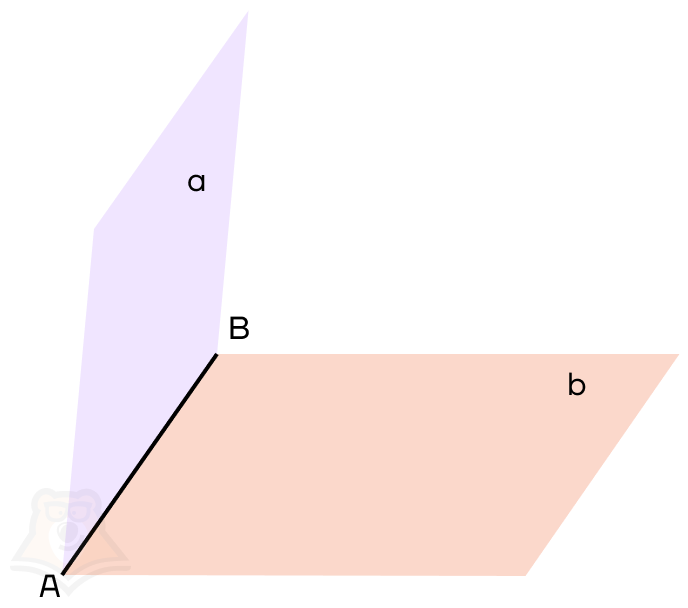
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.

Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.

Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. 

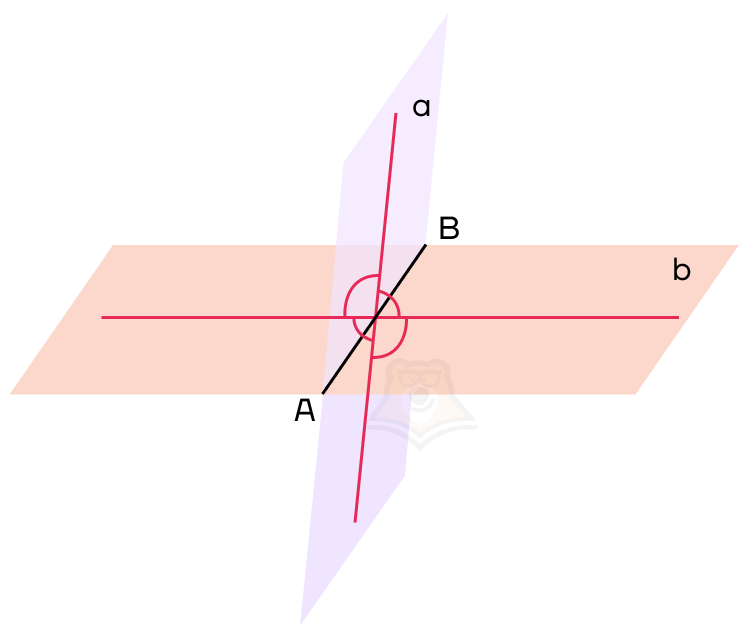
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями. 

Угол COD также будет называться линейным углом двугранного угла. 

Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой. 

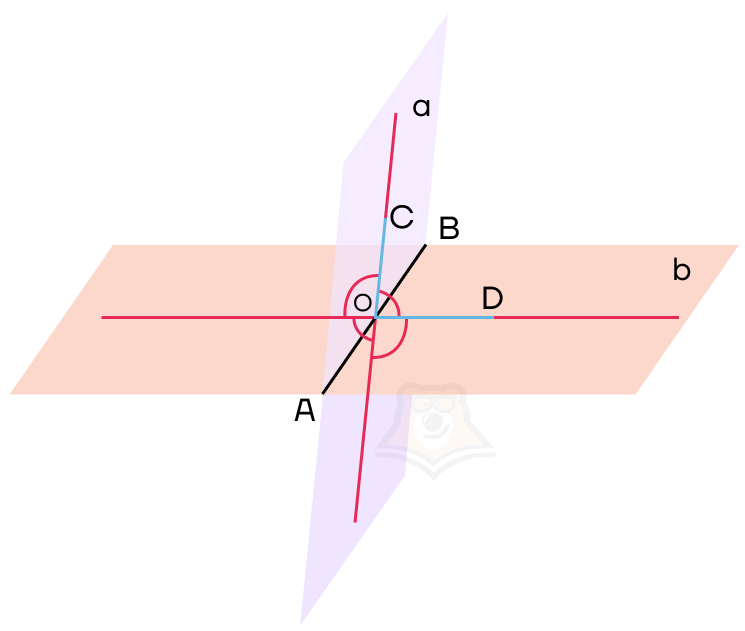
Как и обычные углы, углы между плоскостями бывают трех видов:

• Острые, то есть меньше 90⁰
• Прямые, равные 90⁰
• Тупые, которые больше 90и меньше 180⁰

Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.

А что будет, если между плоскостями получится прямой угол?

Такие плоскости называются перпендикулярными. 

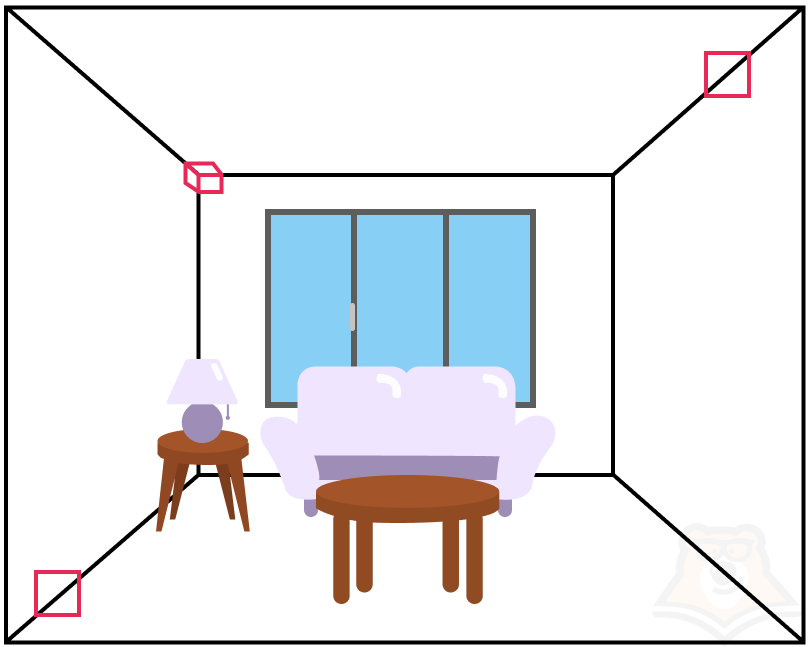
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам. 

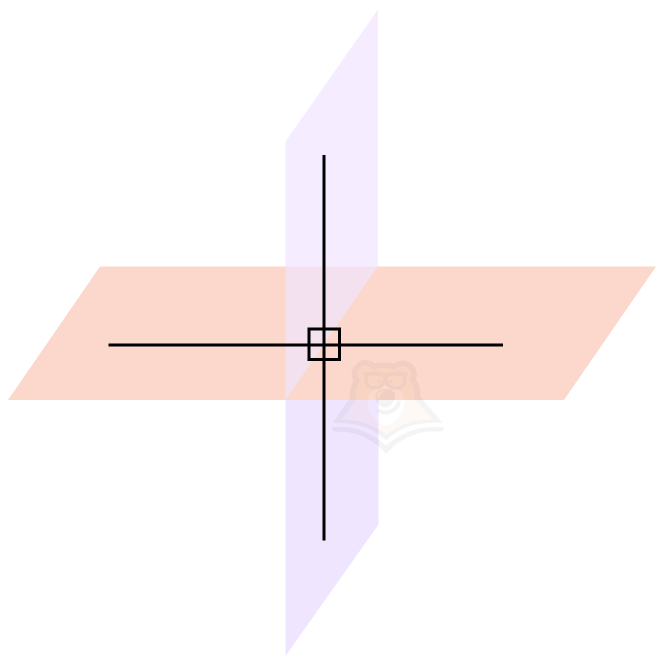
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму. 

Углы между прямой и плоскостью

Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?

И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.

Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. 

Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой. 

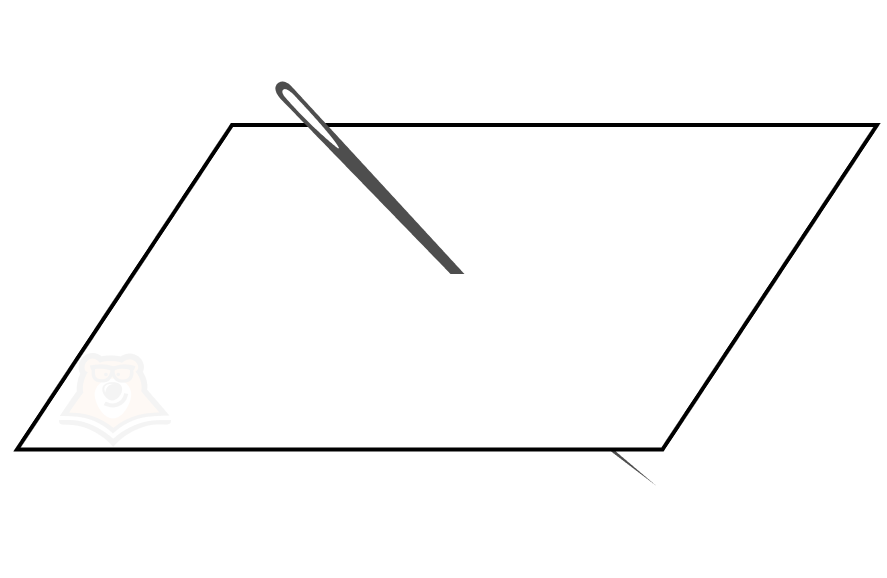
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О. 

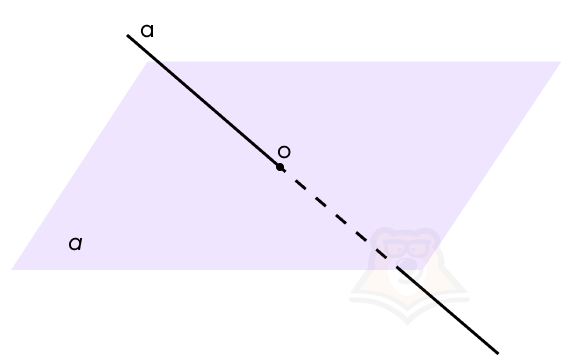
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость. 

Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А₁. 

Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость. 

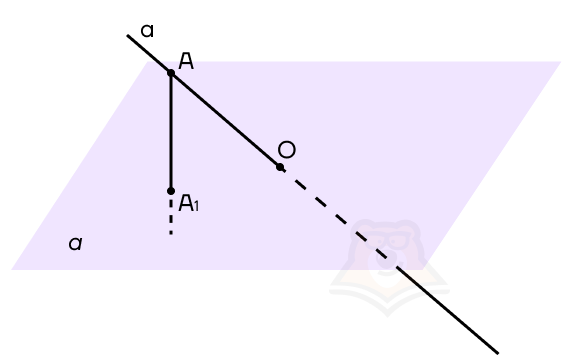
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А₁ и О, получаем, что А₁О — проекция прямой а на плоскость а. 

Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А₁О. 

Проекция прямой а на плоскость — это прямая а₁, образованная проекциями всех точек прямой а на плоскость. 

Таким образом можно построить проекции не только прямой, но и любой фигуры.

Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А₁ОА. 

В этом случае мы также берем острый угол, образованный прямой и плоскостью. 

Если прямая параллельна плоскости угол будет равен 0. 

Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.  

Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.

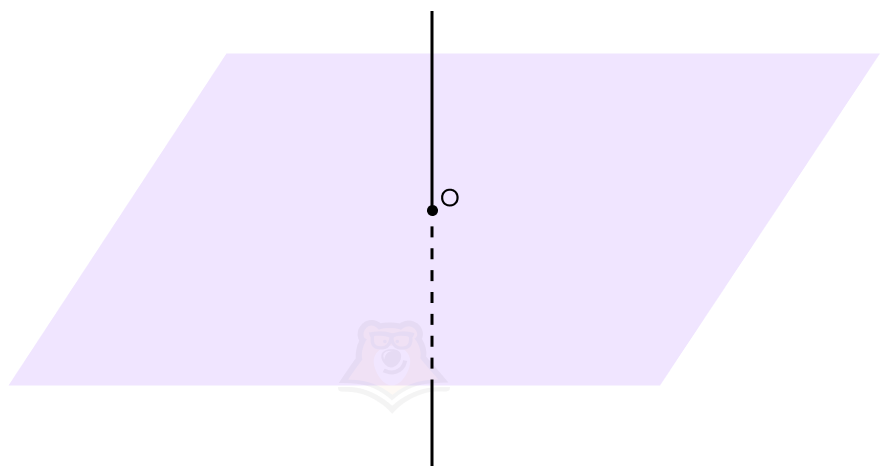
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости. 

Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. 

А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?

Для этого существует признак перпендикулярности прямой и плоскости:

• Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости. 

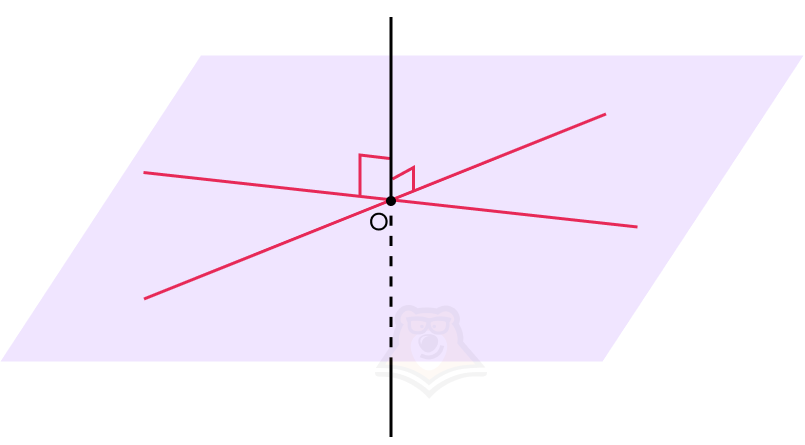
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.

Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости. 

Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости. 

Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет. 

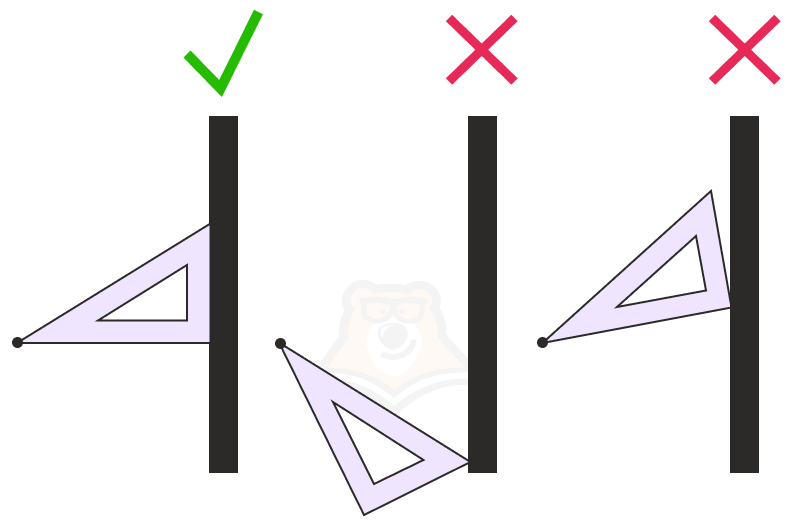
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны. 

Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны. 

Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”. 

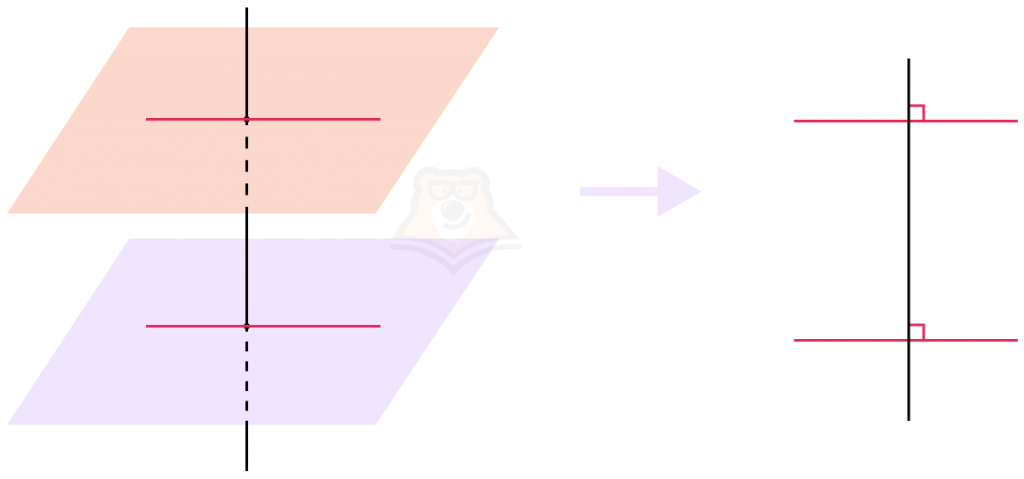
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны. 

Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”. 

Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны. 

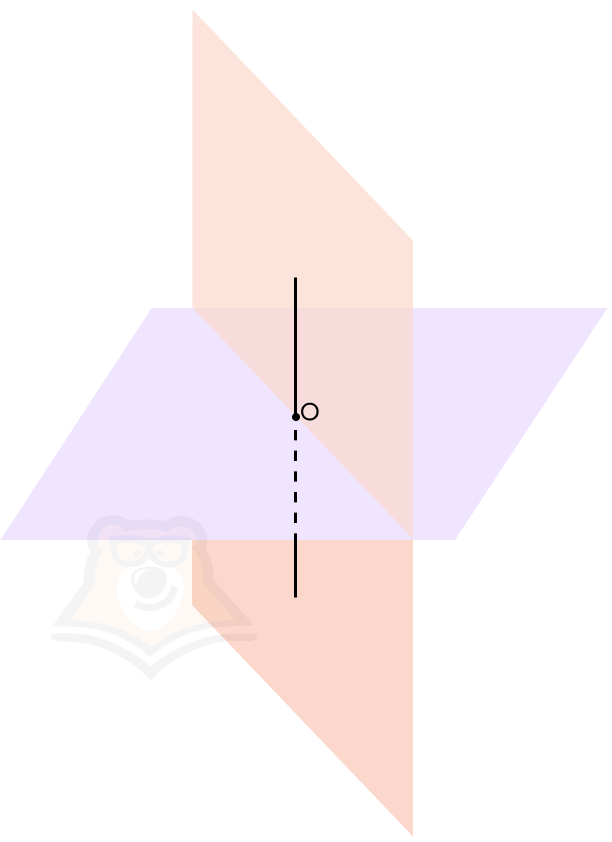
Это легко проверить, если найти любой двугранный угол между построенными плоскостями. 

Теорема о трех перпендикулярах

Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах. 

Для начала попробуем понять ее на реальных предметах. 

Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?

Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол. 

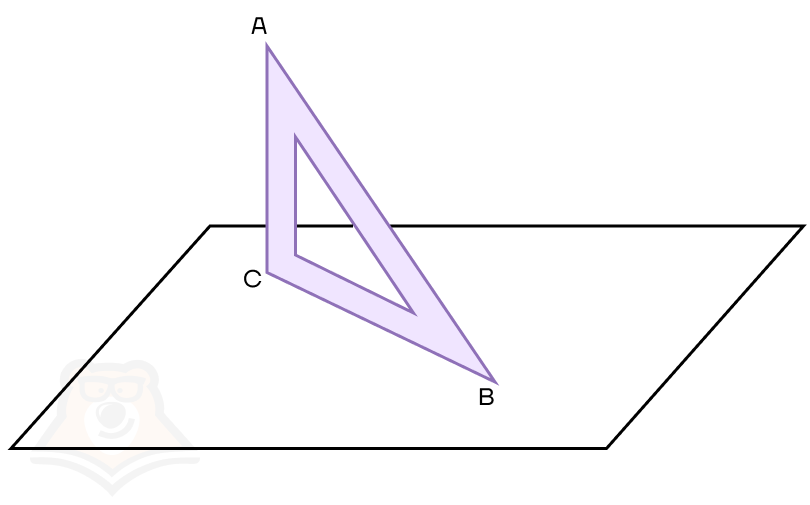
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально). 
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°. 
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.

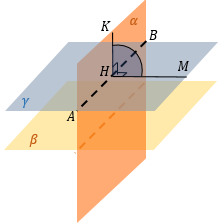
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ. 
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).

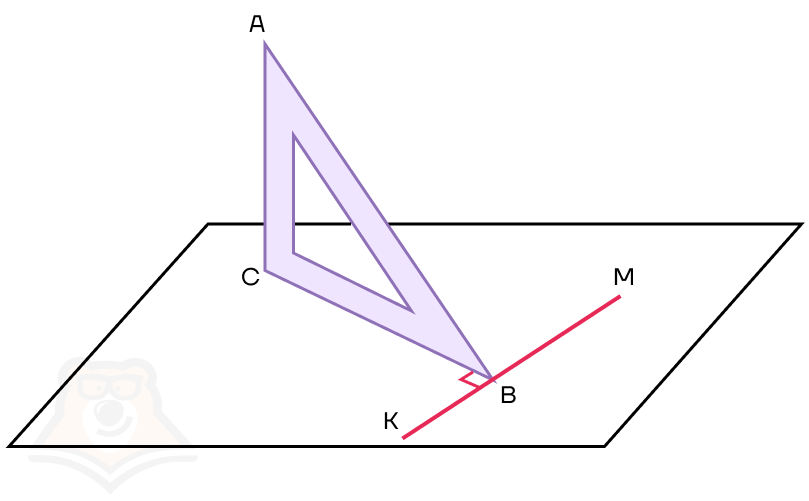
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ. 

Возникнет вопрос, почему? 

1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости. 

Теперь узнаем, как этот признак выполняется в данной ситуации. 

2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку. 

3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости. 

4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ. 

Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции. 

Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком. 

Теорема о трех перпендикулярах 
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ. 

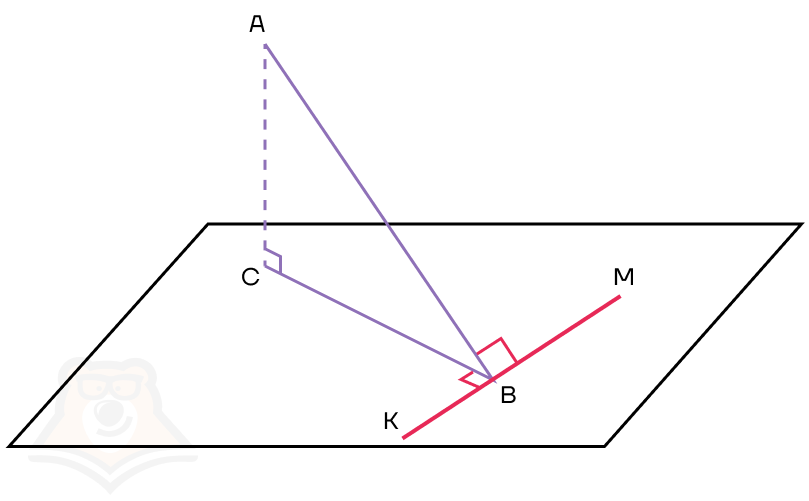
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости. 

Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.

Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач. 

Фактчек

• Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями. 
• Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны. 
• Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°. 
• Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым. 
• Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b. 

Проверь себя

Задание 1. 
Выберите верное утверждение. 

1. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
2. Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
3. Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
4. Ребра двугранного угла — это плоскости, которые его образуют. 

Задание 2. 
Угол между плоскостями — это…

1. Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
2. Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
3. Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
4. Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.

Задание 3. 
Что такое проекция прямой на плоскость?

1. Это любая прямая, проведенная из точки пересечения прямой и плоскости;
2. Это перпендикуляр, опущенный из любой точки на плоскость;
3. Это всегда точка пересечения прямой и плоскости;
4. Это прямая, образованная проекциями всех точек прямой на плоскость. 

Задание 4. 
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?

1. Проекция будет равна этой прямой и параллельна ей;
2. Проекция будет меньше прямой и образовывать с ней угол;
3. Проекция будет точкой пересечения прямой и плоскости;
4. Проекция будет больше прямой и образовывать с ней угол.  

Задание 5. 
Как доказать, что прямая перпендикулярна плоскости?

1. Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
2. Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
3. Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
4. Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.

Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4

Углы

Классическим заданием с развернутым ответом на стереометрию является задача на нахождение угла. В стереометрии найти угол могут предложить между следующими комбинациями фигур:

Рассмотрим каждую комбинацию, чтобы понять, как искать разные виды углов и какие методы можно применять.

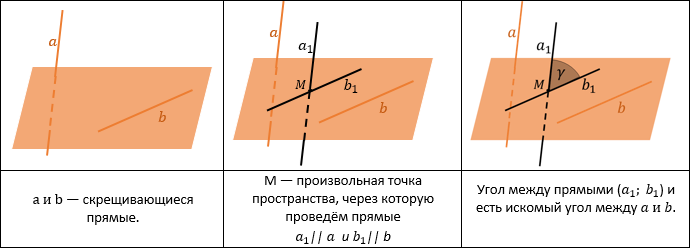
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ

Угол между скрещивающимися прямыми ― это угол между параллельными им прямыми, лежащими в одной плоскости.

Это значит, что никогда не пересекающиеся прямые в пространстве мы делаем «пересекающимися»: для этого нужно построить пересекающиеся прямые, параллельные данным. Угол между ними будет искомым.

Часто достаточно только к одной из скрещивающихся прямых построить параллельную прямую.

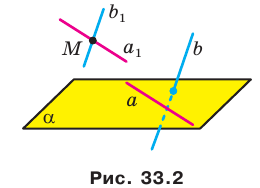
Например, если бы мы отметили точку M на прямой b и через точку M провели прямую $ a_1 parallel a $.

УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ

Угол между прямой и плоскостью — угол между прямой и ее проекцией на эту плоскость.

Для того, чтобы найти угол между прямой и плоскостью, нужно сначала получить проекцию этой прямой на плоскость, а потом найти угол.

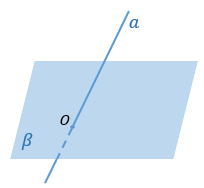
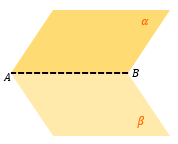
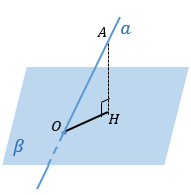
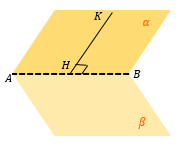
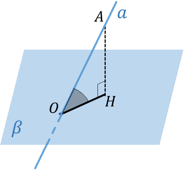
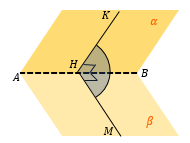
Прямая, пересекающая плоскость β в точке O	Из произвольной точки А на прямой опустим перпендикуляр AH на плоскость β. Тогда OH – проекция прямой на плоскость β.	Угол между прямой и наклонной, то есть ∠ AOH и есть искомый угол между .

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Для начала вспомним пару определений:

Метод перпендикуляров к линии пересечения.Нахождения угла между плоскостями – одна из самых сложных задач на углы, поэтому тут мы можем воспользоваться несколькими методами.

Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это основной способ нахождения угла между плоскостями.

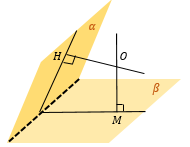
Находим линию пересечения плоскостей α и β – AB.	Из «удобной» точки К в плоскости α (это может быть вершина многогранника, середина ребра и т.д.) опускаем перпендикуляр KH на AB.	В точку H опустим перпендикуляр из точки M в плоскости β. ∠ KHM – искомый угол между плоскостями α и β

• Метод перпендикуляров к плоскостям.

Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям. Этот способ удобен, если перпендикуляр к плоскости построить удобнее, чем построить перпендикуляры к линии пересечения плоскостей (или перпендикуляр к плоскости уже есть по условию задачи).

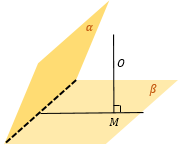
Из произвольной точки O пространства опустим перпендикуляр OM на плоскость β.	Из точки O опустим так же перпендикуляр OH на плоскость α.	Любой из двух смежных углов между OM и OH может считать искомым, но так как угол между плоскостями измеряется от 0 до 90°, то берем острый. ∠ MOK – искомый угол между плоскостями α и β

• Метод параллельных плоскостей.

Угол между плоскостями вычисляется как угол между плоскостями, параллельными данным плоскостям. Этот способ применим, когда угол между данными плоскостями по каким-то причинам искать неудобно, а удобнее найти угол между плоскостями, параллельными данным.

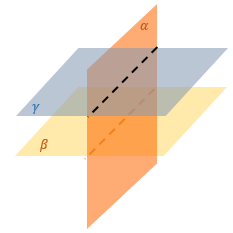
Угол между плоскостями α и β затруднительно искать (например, нет «удобных точек» или тяжело построить взаимные перпендикуляры).	Построим плоскость γ, параллельную β (или в стереометрической фигуре она уже есть)	По методу перпендикуляров к линии пересечения найдем угол между плоскостями α и γ. ∠ MНK – искомый угол между плоскостями α и β

Угол между плоскостями. Перпендикулярность плоскостей

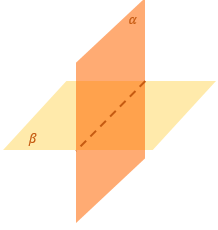
Пусть плоскости α и β пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.

Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны.

Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:

Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.

Читаем дальше: Угол и расстояние между скрещивающимися прямыми.

Содержание:

Перпендикулярность в пространстве

В этом параграфе вы ознакомитесь с понятиями угла между прямыми в пространстве, угла между прямой и плоскостью, угла между двумя плоскостями; узнаете, что такое ортогональная проекция, изучите свой­ство ортогональной проекции многоугольника.

Угол между прямыми в пространстве

Поскольку две любые пересекающиеся прямые пространства лежат в одной плоскости, то угол между ними определим так же, как в планиметрии. Определение. Углом между двумя пересекающимися прямыми называют величину того из углов, образовавшихся при их пересечении, который не превышает (рис. 33.1).

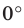
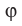
Угол между двумя параллельными прямыми считают равным Следовательно, если — угол между двумя прямыми, лежащими в одной плоскости, то .

Введем понятие угла между скрещивающимися прямыми. Определение. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся пря­мым.

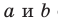
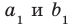
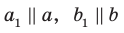
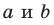
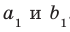
Пусть прямые скрещивающиеся. Через точку М простран­ства проведем прямые так, что (рис. 33.2). По определению угол между скрещивающимися прямыми равен углу между пересекающимися прямыми .

Возникает естественный вопрос: зависит ли угол между данными скрещивающимися прямыми 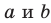от выбора точки М ? Ответить на этот вопрос помогает следующая теорема.

Теорема 33.1. Угол между двумя пересекающимися прямыми равен углу между двумя другими пересекающимися прямыми, соответственно параллельными данным.

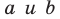
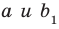
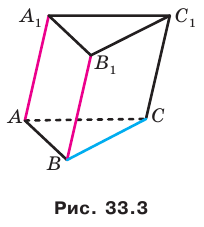
Воспользовавшись теоремой 33.1, можно показать, что угол между скрещивающимися прямыми равен углу между пересекающимися прямыми , где

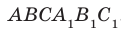
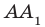
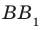
Например, на рисунке 33.3 изображена треугольная призма . Угол между скрещивающимися прямыми и ВС равен углу между пересекающимися прямыми и ВС.

Определение. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Заметим, что перпендикулярные прямые могут как пересекаться, так и быть скрещивающимися.

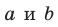
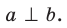
Если прямые перпендикулярны, то записывают: Два отрезка в пространстве называют перпендикулярными, если они лежат на перпендикулярных прямых.

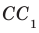
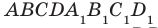
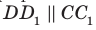
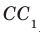
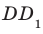
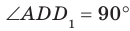
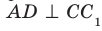
Например, ребра AD и куба перпендикулярны (рис. 33.4). Действительно, поскольку то угол между прямыми AD и равен углу между прямыми AD и . Но , поэтому .

Пример:

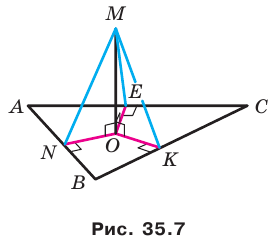
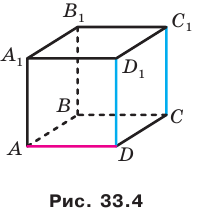
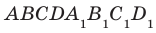
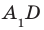
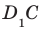
На рисунке 33.5 изображен куб . Най­дите угол между прямыми и .

Решение:

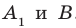
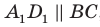
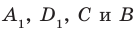
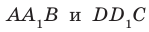
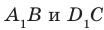
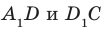
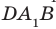
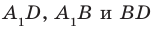
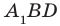
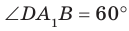
Соединим точки . Поскольку , то точки лежат в одной плоскости. Эта плоскость пересекает параллельные плоскости по параллельным прямым . Следовательно, угол между прямыми равен углу . Соединим точки В и D. Отрезки равны как диагонали равных квадратов. Следовательно, треугольник равносторонний. Тогда . Ответ : 60°.

Перпендикулярность прямой и плоскости

В повседневной жизни мы говорим: флагшток перпендикулярен поверхности земли (рис. 34.1), мачты парусника перпендикулярны поверхности палубы (рис. 34.2), шуруп вкручивают в доску перпендикулярно ее поверхности (рис. 34.3) и т.п.

Эти примеры дают представление о прямой, перпендикулярной плоскости. Определение. Прямую называют перпендикулярной пло­скости, если она перпендикулярна любой прямой, лежащей в этой плоскости (рис. 34.4).

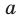
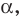
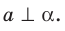
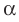
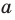
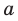
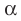
Если прямая перпендикулярна плоскости то записывают: Также принято говорить, что плоскость перпендикулярна прямой или прямая и плоскость перпендикулярны.

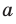
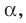
Из определения следует, что если прямая перпендикулярна плоскости то она пересекает эту плоскость.

Отрезок называют перпендикулярным плоскости, если он принадлежит прямой, перпендикулярной этой плоскости.

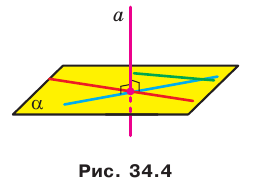
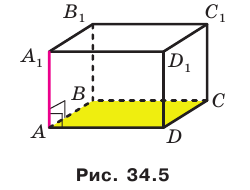
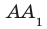
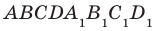
Например, интуитивно понятно, что ребро прямоугольного параллелепипеда перпендикулярно плоскости АВС (рис. 34.5). Доказать этот факт нетрудно, воспользовавшись следующей теоремой.

Теорема 34.1 (признак перпендикулярности прямой и плоскости). Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.

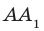
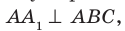
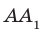
На рисунке 34.5 прямая перпендикулярна двум пересекающимся прямым АВ и AD плоскости АВС. Следовательно, по признаку перпен­дикулярности прямой и плоскости а значит, и ребро также перпендикулярно плоскости АВС.

Теорему 34.1 часто используют на практике. Например, подставка для новогодней елки имеет форму крестовины. Если елку установить так, чтобы ее ствол был перпендикулярен направлениям крестовины, то елка будет стоять перпендикулярно плоскости пола (рис. 34.6).

Приведем теорему, которую можно рассматривать как еще один признак перпендикуляр­ности прямой и плоскости.

Теорем а 34.2. Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости (рис. 34.7).

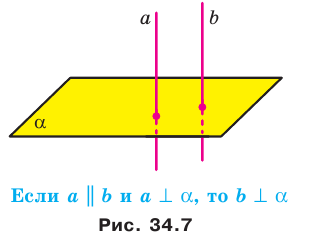
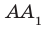
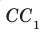
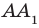
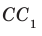
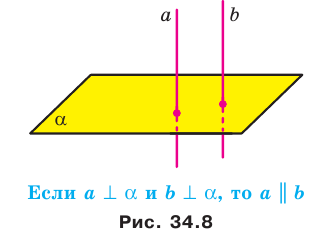
Например, на рисунке 34.5 прямая перпендикулярна плоскости АВС, а прямая параллельна прямой . Следовательно, по теореме 34.2 прямая также перпендикулярна плоскости АВС. Сформулируем теорему, являющуюся признаком параллельности двух прямых.

Теорем а 34.3. Если две прямые перпендикулярны одной и той же плоскости, то они параллельны (рис. 34.8). Справедлива и такая теорема.

Теорема 34.4. Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Пример:

Плоскость 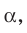перпендикулярная катету АС прямоугольного треугольника АВС, пересекает катет АС в точке Е, а ги­потенузу АВ — в точке F (рис. 34.9). Найдите отрезок EF, если АЕ : ЕС = 3 : 4, ВС = 21 см.

Решение:

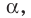
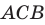
Поскольку прямая АС перпендикулярна плоскости то прямая АС перпендикулярна любой прямой этой плоскости, в частности прямой EF. Прямые EF и ВС лежат в одной плоскости и перпендикулярны прямой АС, поэтому . Из этого следует, что треугольники AEF и подобны. Следовательно, можно записать: EF : СВ=АЕ : АС. Отсюда EF : 21 = 3 : 7, EF = 9 см. Ответ: 9 см.

Перпендикуляр и наклонная

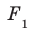
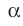
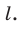
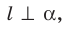
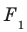
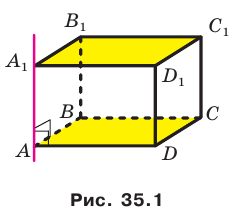
Пусть фигура — параллельная проекция фигуры F на плоскость в направлении прямой Если , то фигуру называют ортогональной проекцией фигуры F на плоскость

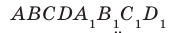
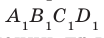
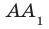
Например, основание ABCD прямоугольного параллелепипеда является ортогональной проекцией основания на пло­скость АВС в направлении прямой (рис. 35.1).

В дальнейшем, говоря о проекции фигуры, если не оговорено противное, будем иметь в виду ортогональную проекцию.

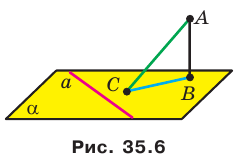
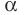
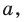
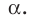
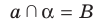
Пусть даны плоскость и не принадлежащая ей точка А . Через точку А проведем прямую перпендикулярную плоскости Пусть (рис. 35.2).

Отрезок АВ называют перпендикуляром, опущенным из точки А на плоскость точку В — основанием перпендикуляра. Основание В перпендикуляра АВ — это проекция точки А на плоскость .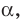

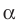
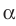
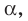
Отметим на плоскости какую-нибудь точку С, отличную от точки В. Проведем отрезок АС (рис. 35.2). Отрезок АС называют наклонной, проведенной из точки А к плоскости точку С — основанием наклонной. Отрезок ВС является проекцией наклонной АС.

Теорема 35.1. Если из одной тонки проведены к плоскости перпендикуляр и наклонная, то наклонная больше перпендикуляра.

Пример:

Докажите, что если точка, не принадлежащая плоскости многоугольника, равноудалена от его вершин, то проекцией этой точки на плоскость многоугольника является центр его описанной окружности.

Решение:

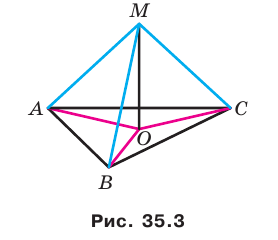
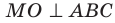
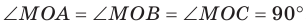
Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Пусть точка М не принадлежит плоскости АВС, причем МА = = МВ = МС. Опустим из точки М перпендикуляр МО на плоскость АВС (рис. 35.3). Докажем, что точка О — центр описанной окружности треугольника АВС. Поскольку , то . В пря­моугольных треугольниках МОА, МОВ, МОС катет МО — общий, гипотенузы равны, следовательно, эти треугольники равны по гипотенузе и катету. Из равенства данных треугольников следует, что ОА = ОВ = ОС, то есть точка О — центр описанной окружности треугольника АВС.

Заметим, что когда надо определить расстояние между двумя геометрическими фигурами, то стремятся найти расстояние между их ближайшими точками. Например, из курса планиметрии вы знаете, что расстоянием от точки, не принадлежащей прямой, до этой прямой называют расстояние от данной точки до ближайшей точки на прямой, то есть длину перпендикуляра, опущенного из точки на прямую. Теорема 35.1 показывает, что целесообразно принять следующее определение.

Определение. Если точка не принадлежит плоскости, то рас­стоянием от точки до плоскости называют длину перпен­дикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Пример:

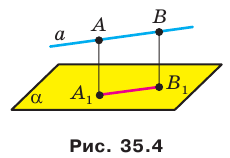
Докажите, что если прямая параллельна плоскости, то все точки прямой равноудалены от плоскости.

Решение:

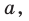
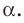
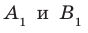
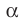
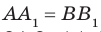
Пусть А и В — две произвольные точки прямой параллельной плоскости Точки — основания перпендикуляров, опущенных соответственно из точек А и В на плоскость (рис. 35.4). Докажем, что .

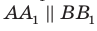
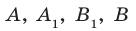
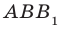
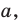
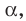
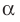
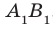
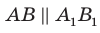
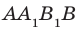
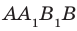
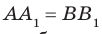
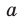
По теореме 34.3 . Следовательно, точки лежат в одной пло­скости. Плоскость проходит через прямую параллельную плоскости и пересекает плоскость по прямой . Тогда по теореме 30.2 получаем: . Таким образом, в четырехугольнике каждые две противолежащие стороны параллельны. Следовательно, четырехугольник — параллелограмм. Отсюда Так как точки А и В выбраны на прямой произвольно, то утверждение задачи доказано.

Доказанное свойство позволяет принять следующее определение. Определение. Расстоянием от прямой до параллель­ной ей плоскости называют расстояние от любой точки этой прямой до плоскости. Используя результат, полученный в ключевой задаче 2, можно решить следующую задачу.

Пример:

Докажите, что если две плоскости параллельны, то все точки одной плоскости равноудалены от другой плоскости. Определение. Расстоянием между двумя параллель­ными плоскостями называют расстояние от любой точки одной плоскости до другой плоскости.

Результаты, полученные в ключевых задачах 2 и 3, часто ис­пользуют в практической деятельности, например в строительстве (рис. 35.5).

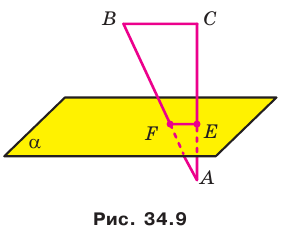
Теорема 35.2 (теорема о трех перпендикулярах). Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

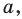
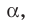
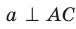
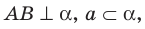
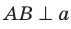
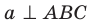
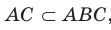
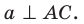
Доказательство. Докажем первую часть теоремы.Пусть прямая принадлежащая плоскости перпендикулярна проекции ВС наклонной АС (рис. 35.6). Докажем, что . Имеем: следовательно, . Получили, что прямая а перпендикулярна двум пересекающимся прямым АВ и ВС плоскости АВС; следовательно,. Поскольку то Доказательство второй части теоремы аналогично доказатель­ству первой части.

Пример:

Точка М не принадлежит плоскости выпуклого многоугольника и равноудалена от всех прямых, содержащих его стороны. Проекцией точки М на плоскость многоугольника является точка О, принадлежащая многоугольнику. Докажите, что точка О — центр вписанной окружности многоугольника.

Решение:

Проведем доказательство для треугольника. Для других многоугольников доказательство будет аналогичным. Опустим из точки О перпендикуляры ON, ОК и ОЕ соответственно на прямые АВ, ВС и СА (рис. 35.7). Соединим точку М с точками Е, К и N.

Отрезок ON является проекцией на­клонной MN на плоскость АВС. По построению 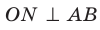. Тогда по теореме о трех перпендикулярах получаем:

Аналогично можно доказать, что 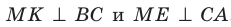. Следовательно, длины отрезков MN, МК и ME — расстояния от точки М до прямых АВ, ВС и СА соответственно. По условию MN = МК = МЕ.

В прямоугольных треугольниках MON, МОК, МОЕ катет МО общий, гипотенузы равны; следовательно, данные треугольники равны по катету и гипотенузе. Из равенства этих треугольников следует, что ON = ОК = ОЕ.

Длины отрезков ON, ОК и ОЕ являются расстояниями от точки О до прямых, содержащих стороны треугольника АВС. Мы показали, что эти расстояния равны. Так как точка О принадлежит треугольнику АВС, то точка О — центр вписанной окружности треугольника АВС.

Угол между прямой и плоскостью

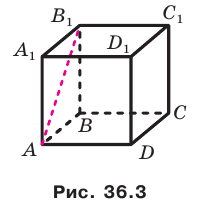
Вы знаете, что в давние времена путешественники ориентировались по звездам. Они измеряли угол, который образовывал с плоскостью горизонта луч, идущий от данной точки к небесному телу.

Сегодня человеку в своей деятельности также важно определять углы, под которыми наклонены к данной плоскости некоторые объекты (рис. 36.1). Эти примеры показывают, что целесообразно ввести понятие угла между прямой и плоскостью.

Определение. Если прямая параллельна плоскости или принадлежит ей, то считают, что угол меж ду такой прямой и плоскостью равен 0°.

Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен .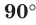

Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость (рис. 36.2).

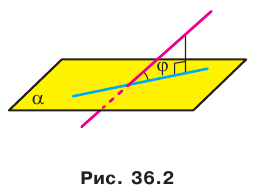
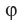
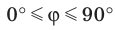
Из определения следует, что если — угол между прямой и плоскостью, то .

Также принято говорить, что прямая образует угол 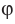с плоскостью.

Углом между отрезком и плоскостью называют угол между прямой, содержащей этот отрезок, и плоскостью.

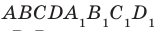
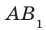
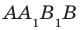
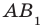
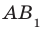
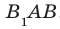
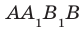
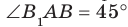
Например, рассмотрим куб (рис. 36.3). Угол между диагональю грани и плоскостью АВС равен 45°. Действительно, прямая АВ — проекция прямой на плоскость АВС. Тогда угол между прямой и плоскостью АВС равен величине угла . Поскольку четырехугольник — квадрат, то .

Пример:

Докажите, что если из одной точки к плоскости проведены наклонные, образующие равные углы с плоскостью, то проекция данной точки на плоскость равноудалена от оснований наклонных.

Решение:

Пусть МЛ и М В — наклонные, образующие с плоскостью 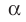равные углы, отрезки ОА и ОВ — проекции этих наклонных (рис. 36.4). Докажем, что ОА = ОВ.

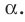
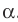
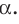
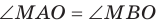
Прямая ОА является проекцией прямой МА на плоскость Так как угол МАО острый, то он равен углу между прямыми ОА и МА. Следовательно, величина угла МАО равна углу между наклонной МА и плоскостью . Аналогично можно доказать, что величина угла МВО равна углу между наклонной МВ и плоскостью По условию .

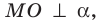
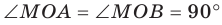
Поскольку то . Получаем, что прямоугольные треугольники МОА и МОВ равны по катету и противолежащему острому углу. Отсюда .

• Заказать решение задач по высшей математике

Двугранный угол. Угол между плоскостями

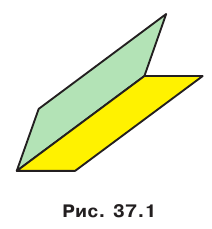
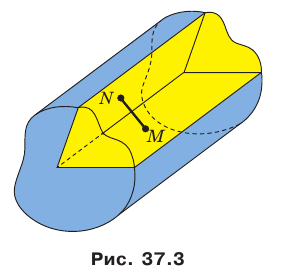
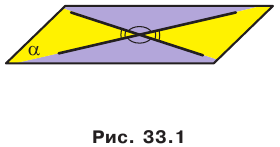
На рисунке 37.1 изображена фигура, состоящая из двух полуплоскостей, имеющих общую границу. Эта фигура делит пространство на две части, выделенные на рисунке 37.2 разными цветами. Каждую из этих частей вместе с полуплоскостями называют двугран­ным углом. Полуплоскости называют гранями двугранного угла, а их общую границу — ребром двугранного угла. Как видим, «желтый» и «синий» двугранные углы, изображенные на рисунке 37.2, существенно различаются. Это различие выражается следующим свойством. На гранях двугранного угла выберем произвольные точки М и N (рис. 37.3).

Отрезок MN принадлежит «желтому» двугранному углу, а «сине­му» двугранному углу принадлежат лишь концы отрезка. В дальнейшем, говоря «двугранный угол», будем подразумевать такой двугранный угол, который содержит любой отрезок с концами на его гранях («желтый» двугранный угол).

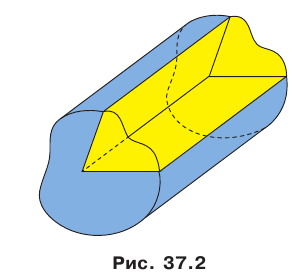
Наглядное представление о двугранном угле дают полуоткрытая классная доска, двускатная крыша, открытый ноутбук (рис. 37.4).

Двугранный угол считают пространственным аналогом угла на плоскости. Вы знаете, как определяют величину угла на плоскости. Научимся определять величину двугранного угла.

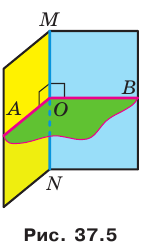
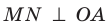
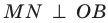
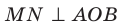
Отметим на ребре MN двугранного угла произ­вольную точку О. Через точку О в гранях двугран­ного угла проведем лучи ОА и ОВ перпендикулярно ребру MN (рис. 37.5). Угол АОВ, образованный этими лучами, называют линейным углом двугран­ного угла. Поскольку и , то . Таким образом, если через произвольную точку ребра двугранного угла провести плоскость перпендикулярно ребру, то эта плоскость пересечет двугранный угол по его линейному углу.

Определение. Величиной двугранного угла называют величину его линейного угла.

Двугранный угол называют острым, прямым, тупым или развернутым, если его линейный угол соответственно острый, прямой, тупой или развернутый.

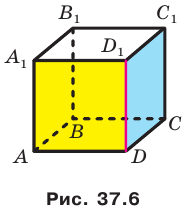
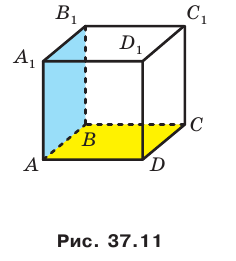
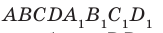
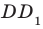
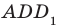
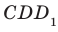
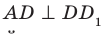
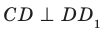
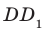
Например, рассмотрим куб (рис. 37.6). Двугранный угол с ребром , грани которого принадлежат плоскостям и является прямым. Действительно, поскольку и , то угол ADC — линейный угол двугранного угла с ребром .

Угол ADC прямой.

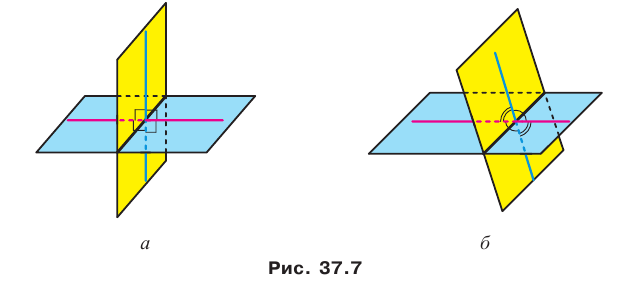
При пересечении двух плоскостей образуются четыре двугранных угла, отличных от развернутого (рис. 37.7). Здесь возможны два случая:

1. все четыре двугранных угла прямые (рис. 37.7, а);
2. из четырех двугранных углов два равных угла острые и два равных угла тупые (рис. 37.7, б).

В обоих случаях из четырех двугранных углов найдется такой, величина которого не превышает 90°.

Определение. Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся дву­гранных углов, который не превышает 90°. Угол между двумя параллельными плоскостям и равен 0°.

Углом между многоугольником и плоскостью, которой много угольник не принадлежит, называют угол между плоскостью, содержащей многоугольник, и данной плоскостью.

Углом между двумя многоугольниками, лежащими в разных плоскостях, называют угол между плоскостями, в которых лежат эти многоугольники.

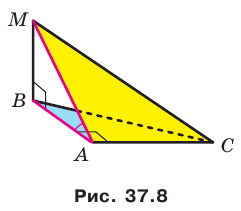
Пример:

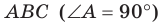
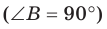
Прямоугольные треугольники и АВМ имеют общий катет АВ (рис. 37.8). Отрезок МВ перпендикулярен плоскости АВС. Известно, что МВ = 4 см, АС = 6 см, МС = 10 см. Найдите угол между плоскостями АВС и АМС.

Решение:

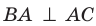
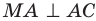
Отрезок ВА является проекцией наклонной МА на плоскость АВС. Так как , то по теореме о трех перпендикулярах . Следователь но, угол МАВ — линейный угол двугранного угла с ребром АС, грани которого принадлежат плоскостям АВС и АМС. Поскольку угол МАВ острый, то угол между плоскостями АВС и АМС равен величине угла МАВ.

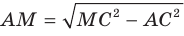
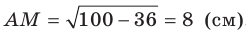
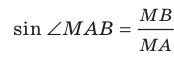
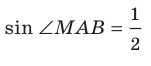
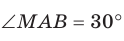
Для стороны AM прямоугольного треугольника АМС можно записать: . Отсюда . Для угла МАВ прямоугольного треугольника МАВ запишем: . Отсюда и . Ответ: 30°.

Имеет место теорема, устанавливающая связь между площадью данного многоугольника и площадью его проекции.

Теорема 37.1 (площадь ортогональной проекции мно­гоугольника). Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где .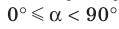

Определение. Две плоскости называют перпендикулярными, если угол между ними равен 90°.

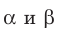
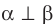
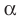
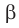
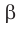
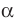
Если плоскости перпендикулярны, то записывают: . Также принято говорить, что плоскость перпендикулярна плоскости или плоскость перпендикулярна плоскости .

Наглядное представление о перпендикулярных плоскостях дают плоскости стены и потолка комнаты, плоскости двери и пола, плоскости сетки и теннисного корта (рис. 37.9).

Очевидно, что перпендикулярные плоскости при пересечении образуют четыре прямых двугранных угла (рис. 37.10).

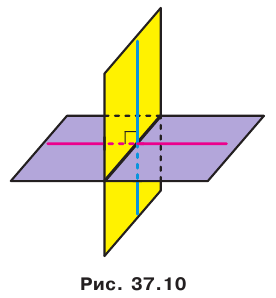
Теорема 37.2 (признак перпендикулярности плоско­стей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

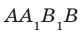
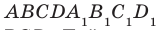
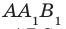
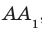
Например, плоскость грани прямоугольного параллелепипеда , (рис. 37.11) перпендикулярна плоскости грани ABCD. Действительно, плоскость проходит через прямую , перпендикулярную плоскости АВС.

ГЛАВНОЕ В ПАРАГРАФЕ 5

Угол между прямыми в пространстве Углом между двумя пересекающимися прямыми называют ве­личину того из углов, образовавшихся при их пересечении, который не превышает 90°. Считают, что угол между двумя параллельными прямыми равен 0°. Углом между двумя скрещивающимися прямыми называют угол между пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым. Две прямые в пространстве называют перпендикулярными, если угол между ними равен 90°.

Перпендикулярность прямой и плоскости

• Прямую называют перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
• Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна самой плоскости.
• Если одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна этой плоскости.
• Если две прямые перпендикулярны одной и той же плоскости, то они параллельны.
• Через данную точку можно провести прямую, перпендикулярную данной плоскости, и притом только одну.

Ортогональная проекция фигуры

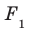
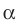
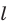
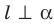
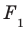
Пусть фигура — параллельная проекция фигуры F на плоскость в направлении прямой . Если , то фигуру называют ортогональной проекцией фигуры F на плоскость

Расстояние от точки до плоскости

Если точка не принадлежит плоскости, то расстоянием от точки до плоскости называют длину перпендикуляра, опущенного из точки на плоскость. Если точка принадлежит плоскости, то считают, что расстояние от точки до плоскости равно нулю.

Расстояние от прямой до параллельной ей плоскости

Расстоянием от прямой до параллельной ей плоскости называют расстояние от любой точки этой прямой до плоскости.

Расстояние между двумя параллельными плоскостями

Расстоянием между двумя параллельными плоскостями назы­вают расстояние от любой точки одной плоскости до другой плоскости.

Теорема о трех перпендикулярах

Если прямая, принадлежащая плоскости, перпендикулярна проекции наклонной к этой плоскости, то она перпендикулярна и самой наклонной. И наоборот, если прямая, принадлежащая плоскости, перпендикулярна наклонной к этой плоскости, то она перпендикулярна и проекции наклонной на эту плоскость.

Угол между прямой и плоскостью

• Если прямая параллельна плоскости или принадлежит ей, то считают, что угол между такой прямой и плоскостью равен 0°.
• Если прямая перпендикулярна плоскости, то считают, что угол между такой прямой и плоскостью равен 90°.
• Если прямая пересекает плоскость и не перпендикулярна ей, то углом между такой прямой и плоскостью называют угол между прямой и ее проекцией на плоскость.

Величина двугранного угла

Величиной двугранного угла называют величину его линейного угла.

Угол между двумя пересекающимися плоскостями

Углом между двумя пересекающимися плоскостями называют величину того из образовавшихся двугранных углов, который не превышает 90°.

Площадь ортогональной проекции многоугольника

Площадь проекции выпуклого многоугольника равна произведению его площади и косинуса угла а между многоугольником и его проекцией, где

Перпендикулярные плоскости

Две плоскости называют перпендикулярными, если угол между ними равен 90°.

Признак перпендикулярности плоскостей

Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.