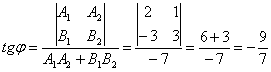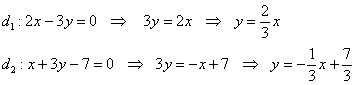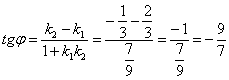На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
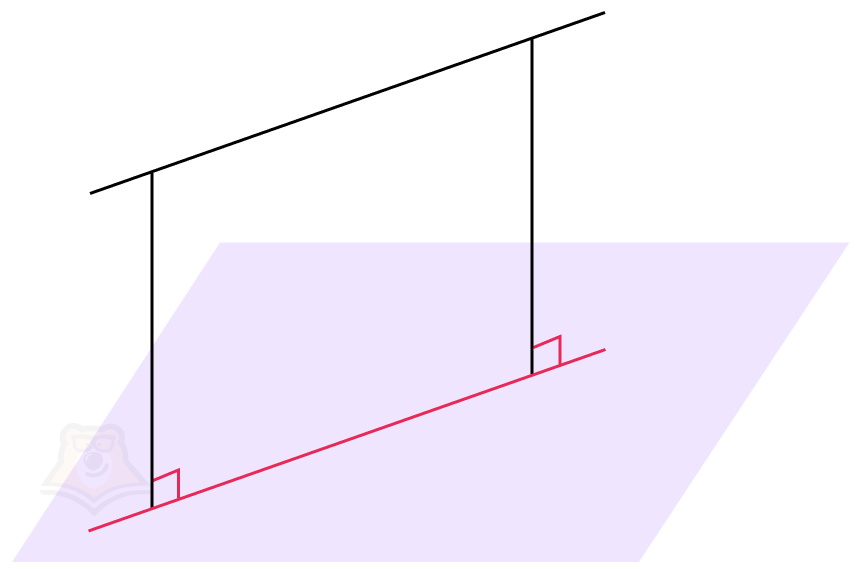
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
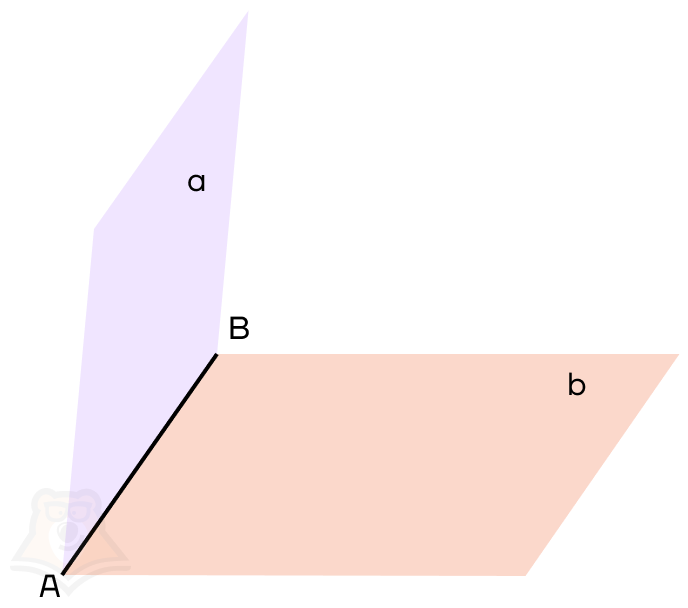
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
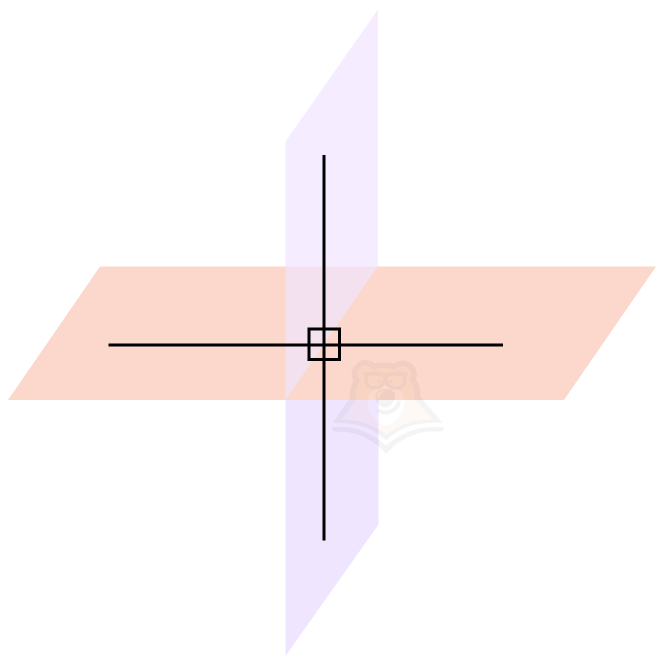
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
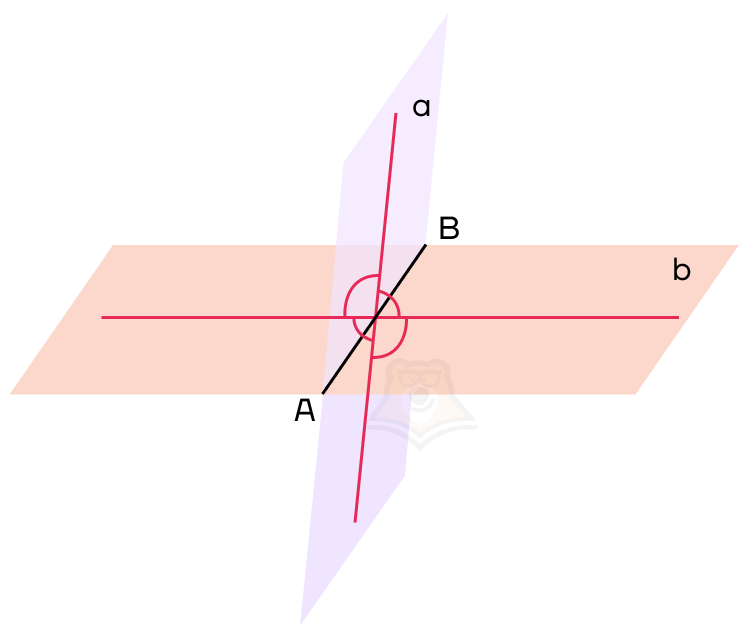
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
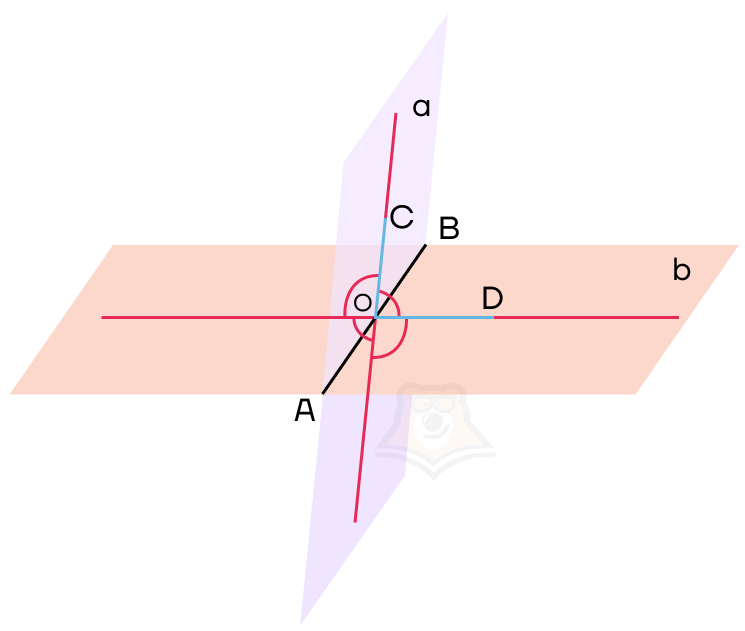
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
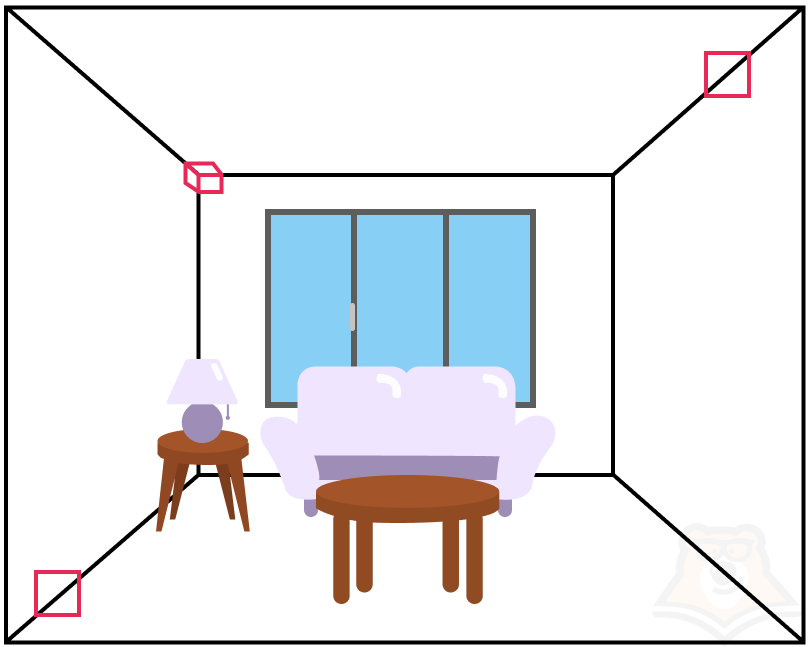
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
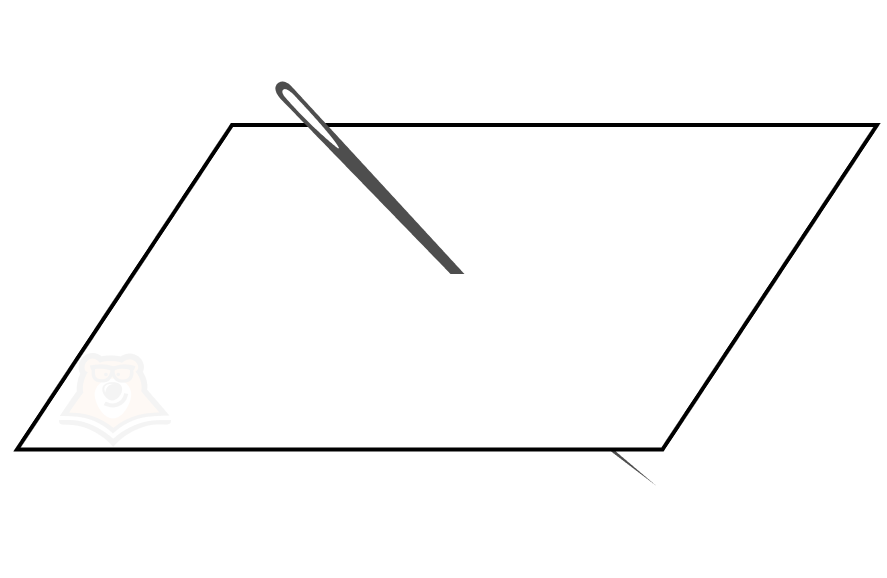
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
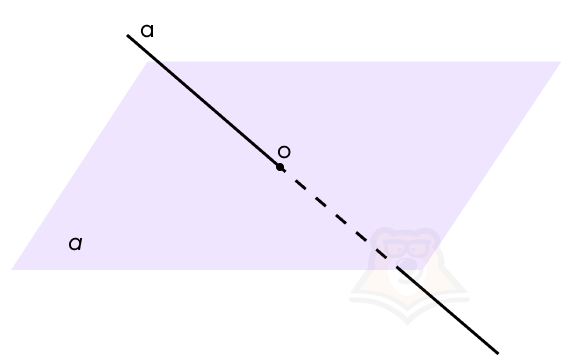
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
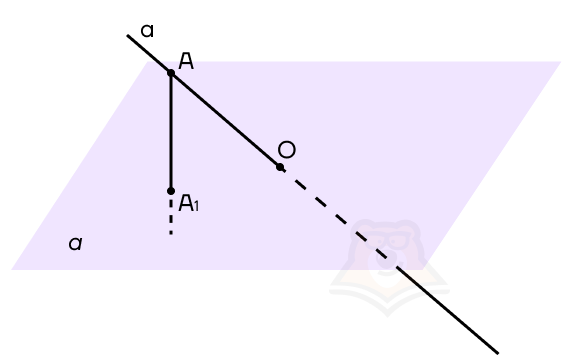
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
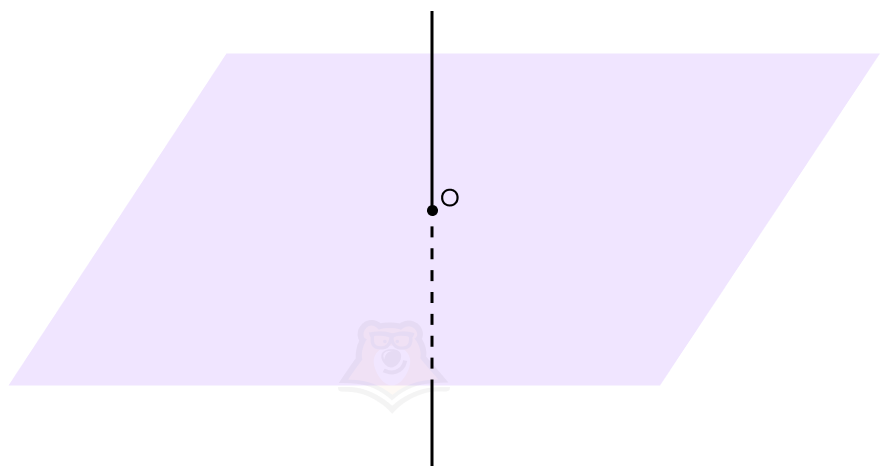
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
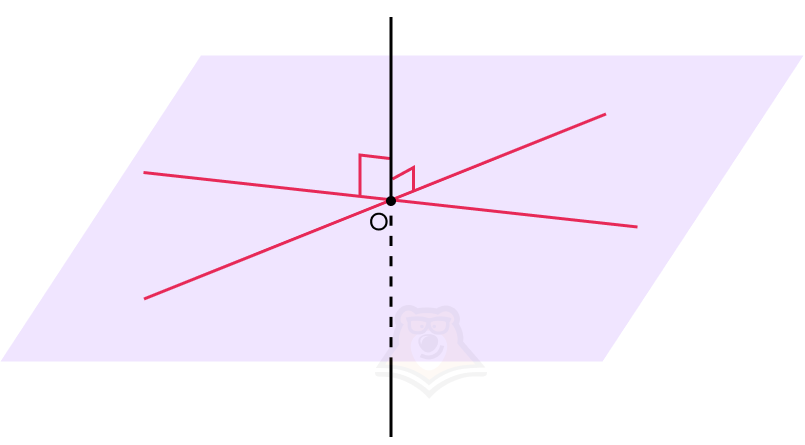
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
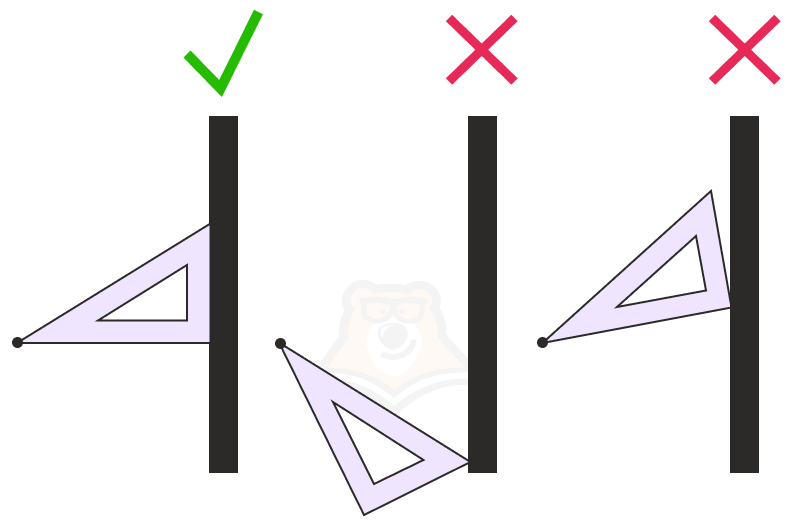
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
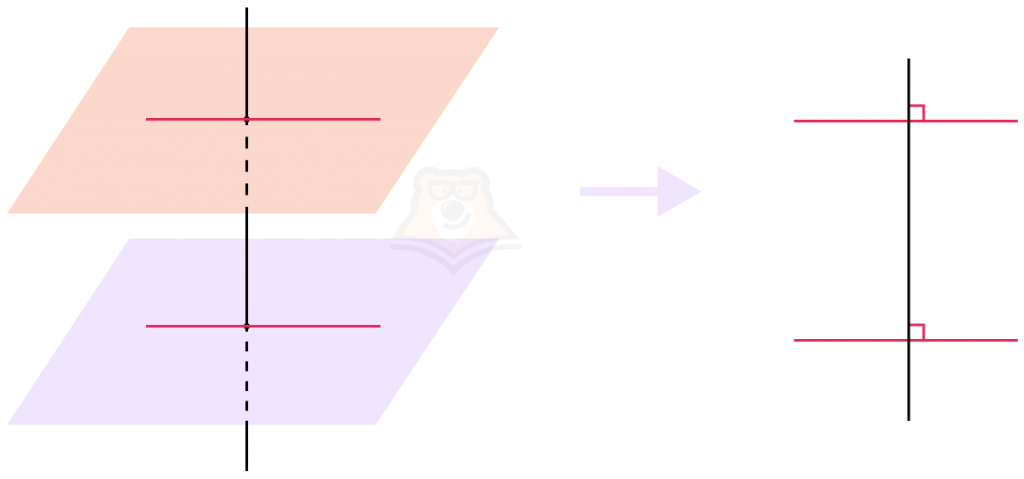
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
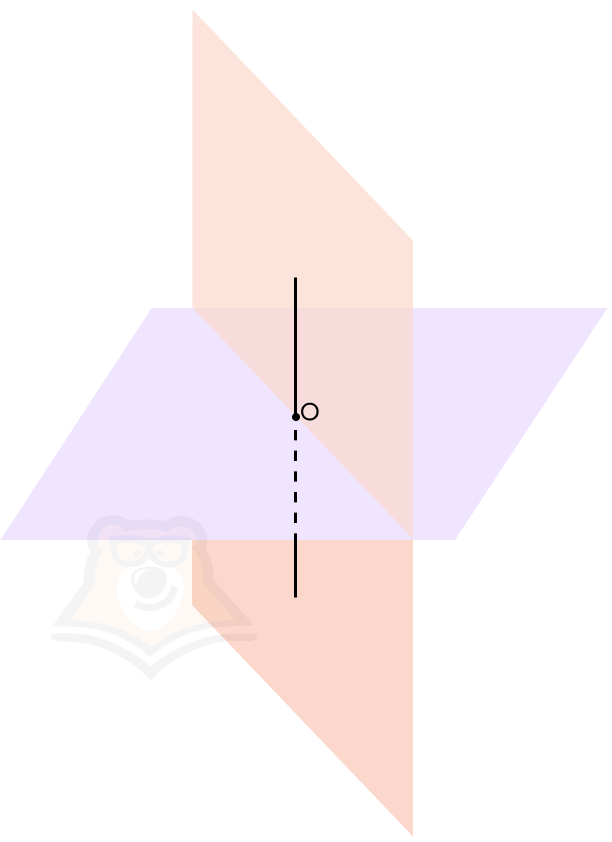
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
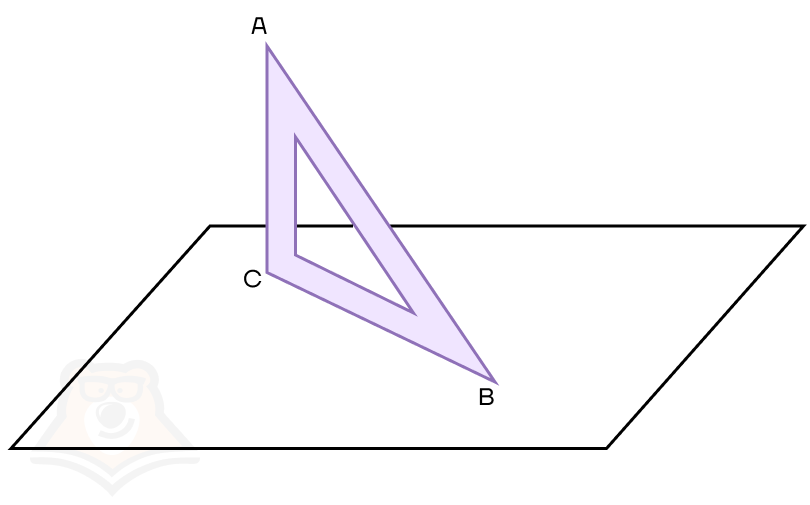
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
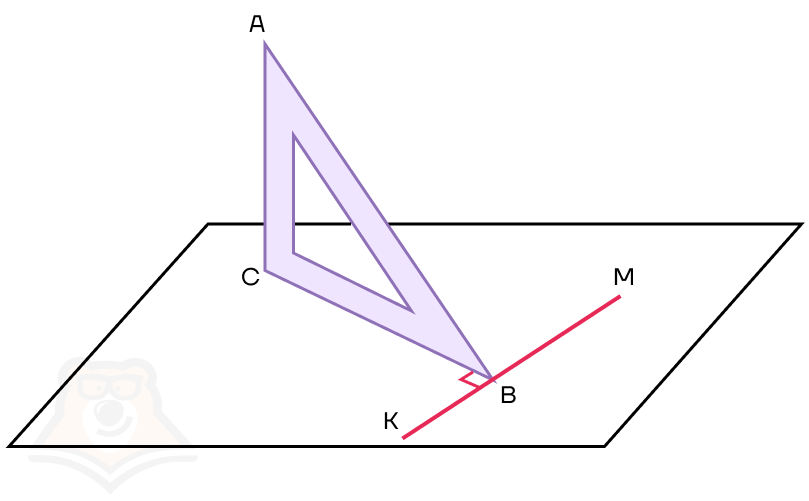
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
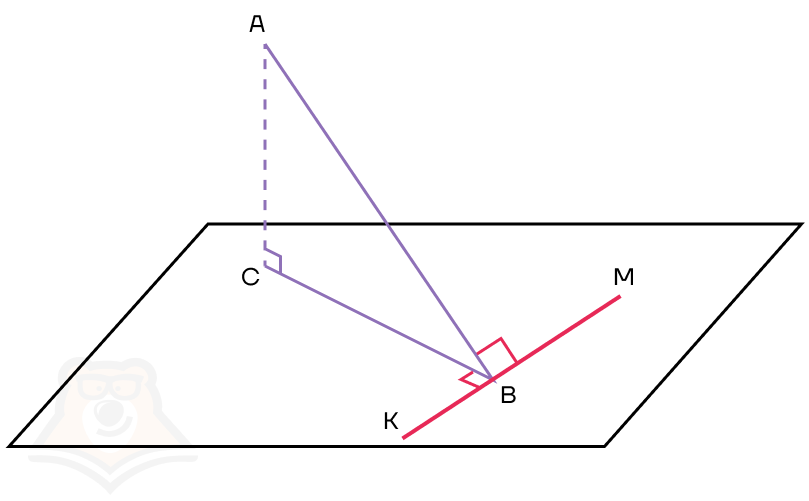
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
Содержание
Длина дуги, угол между линиями, площадь области на поверхности
Краткие теоретические сведения
Зная первую квадратичную форму поверхности, мы можем решить три задачи:
1. Найти длину дуги на поверхности:
begin{equation*}
s=intlimits_{t_1}^{t_2}|vec{r’}(t)dt|=intlimits_{P_1}^{P_2}|dvec{r}(u,v)|=intlimits_{P_1}^{P_2}sqrt{I_1}.
end{equation*}
begin{equation*}
s=intlimits_{t_1}^{t_2}sqrt{Eleft(frac{du}{dt}right)^2+2Ffrac{du}{dt}frac{dv}{dt}+Gleft(frac{dv}{dt}right)^2}dt.
end{equation*}
2. Найти угол между двумя линиями на поверхности в точке их пересечения:
Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле:
begin{gather*}
mbox{cos},varphi = displaystylefrac{I_1(d,delta)}{sqrt{I_1(d)}cdotsqrt{I_1(delta)}} \
mbox{cos},varphi = displaystylefrac{E,du,delta u+F,(du,delta v+delta u,dv)+G,dv,delta v}{sqrt{E,du^2+2F,du,dv+G,dv^2}cdotsqrt{E,delta u^2+2F,delta u,delta v+G,delta v^2}}.
end{gather*}
Говорим, что кривая на поверхности $vec{r}=vec{r}(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec{r}=vec{r}_udu+vec{r}_vdv$ является касательным вектором кривой в этой точке.
3. Найти площадь области $Omega$ на поверхности:
begin{equation*}
S = iintlimits_{D}sqrt{EG-F^2}du,dv,
end{equation*}
где $D$ — прообраз $Omega$ на плоскости $(u,v)$.
Решение задач
Задача 1 (почти Феденко 684)
Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2u,dv^2
end{equation*}
между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.
Решение задачи 1
begin{equation*}
E=1, ,, F=0,,, G=frac19,mbox{sh}^2u.
end{equation*}
begin{equation*}
v=3u ,, Rightarrow ,,dv=3du.
end{equation*}
begin{equation*}
I_1=du^2+frac19,mbox{sh}^2ucdot9,du^2=(1+mbox{sh}^2u)du^2=mbox{ch}^2u,du^2.
end{equation*}
begin{equation*}
s=left|intlimits_{u_1}^{u_2} mbox{ch},u,duright| = |mbox{sh},u_2-mbox{sh},u_1|.
end{equation*}
Задача 2 (почти Феденко 682)
Под каким углом пересекаются линии
$$ u+v=a, ,, u-v=a,$$
лежащие на поверхности:
begin{equation*}
x=u,mbox{cos}v, ,, y=u,mbox{sin},v, ,, z=au.
end{equation*}
Решение задачи 2
Первая квадратичная форма данной поверхности:
begin{equation*}
I_1=(1+a^2),du^2+u^2,dv^2.
end{equation*}
Данные линии пересекаются в точке:
begin{equation*}
left{
begin{aligned}
u+v&=a,\
u-v&=a.
end{aligned}
right. quad Rightarrow quad P(u=a,v=0).
end{equation*}
Направления данных линий:
begin{equation*}
du+dv=0, ,, delta u-delta v=0,, Rightarrow
end{equation*}
begin{equation*}
du = -dv, ,, delta u = delta v.
end{equation*}
Подставляем всё в формулу:
begin{gather*}
mbox{cos},varphi = displaystylefrac{(1+a^2),du,delta u + u^2,dv,delta v}{sqrt{(1+a^2),du^2+u^2,dv^2}cdotsqrt{(1+a^2),delta u^2+u^2,delta v^2}} = \
= left( dv = -du, ,, delta v = delta u right) = \
= displaystylefrac{(1+a^2- u^2),du,delta u}{sqrt{(1+a^2+u^2)^2,du,delta u}}= frac{1+a^2-u^2}{1+a^2+u^2}=\
= left(P(u=a,v=0)right) = \
= frac{1}{1+2a^2}.
end{gather*}
Задача 3
Дана поверхность:
$$z=axy.$$
Найти углы между координатными линиями.
Решение задачи 3
Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$.
Запишем коэффициенты первой квадратичной формы:
begin{align*}
&E=1+(z_x)^2=1+a^2y^2,\
&F=z_xz_y=a^2xy, \
&G=1+(z_y)^2=1+a^2x^2.
end{align*}
Направления координатных линий:
begin{align*}
&x=x_0 ,, Rightarrow dx=0,\
&y=y_0 ,, Rightarrow delta y=0.
end{align*}
Угол между линиями $x=x_0$, $y=y_0$ в точке $(x_0,y_0)$:
begin{align*}
&mbox{cos}, varphi = displaystylefrac{E,dx,delta x + F(dxdelta y+delta xdy)+Gdydelta y}{sqrt{Edx^2+2Fdxdy+Gdy^2}cdotsqrt{Edelta x^2+2Fdelta xdelta y+Gdelta y^2}}=\
&= displaystylefrac{Fdelta xdy}{sqrt{Gdy^2}cdotsqrt{Edelta x^2}}=displaystylefrac{(a^2x_0y_0)delta xdy}{sqrt{(1+a^2x_0^2)dy^2}cdotsqrt{(1+a^2y_0^2)delta x^2}}=\
& = displaystylefrac{a^2x_0y_0}{sqrt{(1+a^2x_0^2) }cdotsqrt{(1+a^2y_0^2) }}.
end{align*}
Задача 4 (Дополнение к Задаче 3)
Как мы вывели в примере выше, угол между координатными линиями равен
begin{equation*}
mbox{cos}, varphi = displaystylefrac{F}{sqrt{EG}}.
end{equation*}
Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.
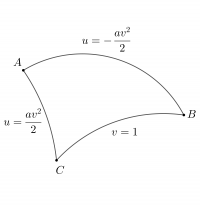
Задача 5 (Феденко 683)
Найти периметр и внутренние углы криволинейного треугольника
$$ u=pm av^2/2,,, v=1,$$
расположенного на поверхности
$$I_1=du^2+(u^2+a^2)dv^2.$$
Вершины треугольника:
begin{align*}
&A(u=0,, v=0),\
&B(u=-frac{a}{2},, v=1), \
&C(u=frac{a}{2},, v=1).
end{align*}
Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника:
begin{align*}
&s_1 = |BC| = a,\
&s_2 = |AC| = frac76 a,\
&s_3 = |BC| = frac76 a,\
&P_{triangle ABC}=s_1+s_2+s_3=frac{10}{3}a.
end{align*}
begin{align*}
&mbox{cos},A = 1, ,, mbox{cos},B=mbox{cos},C=frac23.
end{align*}
Определение угла между прямыми
Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.
Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α — β
tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k1 — k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых
Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x — x0 l = y — y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых
Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; —k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 — k21 + k1·k2
=
2 — (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x — 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ =
k1 — k21 + k1·k2
=
-23 — 431 + (-23)·43
=
-631 — 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x — x0 l = y — y0m = z — z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t — 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x — 23
=
y4
=
z — 35
и —
x — 22
= 1 — 3y =
3z — 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
—x — 22 = x — 2-2
1 — 3y = 1 + y-1/3 = y — 1/3-1/3
3z — 52 = z — 5/32/3
Получено уравнение второй прямой в канонической форме
x — 2-2 = y — 1/3-1/3 = z — 5/32/3
{-2; -13; 23} — направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
Угол между прямыми на плоскости
Определение. Если
заданы две прямые y = k1 x
+ b1 ,
y = k2x
+ b2 ,
то острый угол между этими прямыми будет
определяться как

Две
прямые параллельны, если k1 =
k2 .
Две прямые перпендикулярны, если k1 =
-1/ k2 .
Теорема. Прямые
Ах + Ву + С = 0 и А 1 х
+ В1 у
+ С1 =
0 параллельны, когда пропорциональны
коэффициенты А1 =
λА, В1 =
λВ. Если еще и С1 =
λС, то прямые совпадают. Координаты
точки пересечения двух прямых находятся
как решение системы уравнений этих
прямых.
Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
Определение. Прямая,
проходящая через точку М1 (х1 ,
у1 )
и перпендикулярная к прямой у = kx + b
представляется уравнением:
Расстояние от точки до прямой
Теорема. Если
задана точка М(х0 ,
у0 ),
то расстояние до прямой Ах + Ву + С =0
определяется как

Доказательство. Пусть
точка М 1(х 1,
у 1)
– основание перпендикуляра, опущенного
из точки М на заданную прямую. Тогда
расстояние между точками М и М1 :
(1)
Координаты
x1 и
у1 могут
быть найдены как решение системы
уравнений:
Второе
уравнение системы – это уравнение
прямой, проходящей через заданную точку
М 0 перпендикулярно
заданной прямой. Если преобразовать
первое уравнение системы к виду:
A(x –
x 0 )
+ B(y – y0 )
+ Ax0 +
By0 +
C = 0,
то,
решая, получим:
Подставляя
эти выражения в уравнение (1), находим:
Теорема
доказана.
Пример.
Определить угол между прямыми: y = -3 x +
7; y = 2 x + 1.
k 1 =
-3; k 2 =
2; tgφ = 
φ= p /4.
Пример.
Показать, что прямые 3х – 5у + 7 = 0 и 10х +
6у – 3 = 0 перпендикулярны.
Решение.
Находим: k 1 =
3/5, k2 =
-5/3, k 1* k 2 = -1, следовательно, прямые
перпендикулярны.
Пример.
Даны вершины треугольника А(0; 1), B (6; 5),
C (12; -1). Найти уравнение высоты, проведенной
из вершины С.
Решение.
Находим уравнение стороны АВ: 
4 x = 6 y – 6;
2 x –
3 y + 3 = 0;
Искомое
уравнение высоты имеет вид: Ax + By + C = 0
или y = kx + b . k = .
Тогда y = 
Т.к. высота проходит через точку С, то
ее координаты удовлетворяют данному
уравнению: 
b = 17. Итого: .
Ответ:
3 x + 2 y – 34 = 0.
-
Криві
та поверхні другого порядку. Канонічні
рівняння кривих другого порядку (еліпс,
коло, гіпербола, парабола). Їх властивості.
|
Кривые |
||||||||||||||||||||||||||||
|
Типові практичні
завдання.
-
Знайти
загальний розв’язок неоднорідної
системи лінійних рівнянь за методом
Гауса -
Обчислити
комплексні корені:
.
-
Знайти
ГМТ:
.
-
З’ясувати,
чи є вектор
лінійною комбінацією векторів
?
.
-
Знайти
ранг системи векторів,
базу та подати решту векторів у вигляді
лінійної комбінації векторів з цієї
бази
,
.
-
Обчислити
визначник:
.
-
Обчислити
значення многочлена
від
матриці.
-
Знайти
обернену матрицю до матриці
.
-
Знайти
загальний розв’язок неоднорідної
системи лінійних рівнянь та фундаментальну
систему розв’язків відповідної
однорідної СЛР.

-
Знайти
ранг матриці в залежності від значення
параметру
.

-
Знайти
найбільший спільний дільник многочленів
і
.
-
Визначити
кратність кореня
многочлена
.
-
Відділити
кратні корені многочлена -
Побудувати
многочлен найменшого степеня, який має
корінь (-1) кратності 2; корені 3, 2-i,I—
прості, якщо коефіцієнти цього многочлена
– дійсні, комплексні. -
Знайти
базиси суми та перетину підпросторів
та
.
-
Довести,
що многочлени
утворюють базис простору
,
якщо.
-
Довести,
що кожна з двох систем векторів утворює
базис, та побудувати матрицю переходу
від базису Е до Е´, де
Е:
,
,
;
Е´:,
,
.
-
Розглянемо
площину
.
—
Знайти відстань від
до площини ;
—
Скласти рівняння площини, що проходить
через А паралельно площині.
-
Відомі
координати вершин тетраедра
.
—
Обчислитиоб’ємтетраедра.
— Скласти загальне
рівняння однієї
грані та канонічне рівняння одного
ребра тетраедра.
— Обчислити площу
трикутника АВС.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
2.5.7. Как найти угол между прямыми?
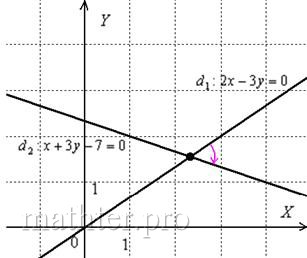
Новая картинка за очередным поворотом:
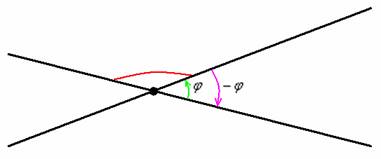
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед или
отрицательно ориентированный «малиновый» угол . Если прямые
перпендикулярны, то за угол между ними можно принять любой из 4 углов.
…что-то не понятно? Срочно изучаем Приложение Тригонометрия!
Однако ещё раз: чем отличаются углы ? Ориентацией (направлением «прокрутки» угла).
Напоминаю, что отрицательно ориентированный угол «прокручивается» по часовой стрелке и записывается со знаком «минус».
Следует отметить, что ориентацию угла часто не принимают во внимание, и рассматривают «просто угол», который .
Как найти угол между двумя прямыми? Существуют три основные формулы.
Способ первый. Рассмотрим две прямые, заданные общими уравнениями в декартовой системе
координат:
Если , то прямые перпендикулярны (
либо
).
Если , то прямые не перпендикулярны и ориентированный угол
между ними можно вычислить с помощью
формулы:
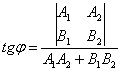
Знаменатель этой формулы – в точности, скалярное произведение направляющих векторов: ,
которое равно нулю тогда и только тогда, когда векторы ортогональны. …надеюсь, не забыли.
Задача 83
Найти угол между прямыми , заданными в декартовой системе координат.
Исходя из вышесказанного, решение удобно оформить в два шага:
1) Вычислим произведение:
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём с помощью формулы:
И с помощью обратной функции (см. Приложение Тригонометрия) легко найти сам угол, при этом используем нечётность арктангенса:
Ответ:
В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью
калькулятора.
Ну, минус, так минус, ничего страшного, вот геометрическая иллюстрация:
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи «первым номером» идёт прямая и «открутка» угла началась именно с неё. Если очень хочется получить положительное значение, то нужно
поменять прямые местами, то есть коэффициенты взять из второго уравнения
, а коэффициенты
– из первого уравнения
. Короче
говоря, начать нужно
с прямой .
Скрывать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.
Способ второй, он удобен, когда прямые заданы уравнениями с
угловым коэффициентом: (в декартовых координатах).
Если , то прямые перпендикулярны (
либо
).
Если , то ориентированный угол
между ними можно найти с помощью формулы:
, и на самом деле это частный случай предыдущей формулы.
К слову, из равенства следует полезная взаимосвязь угловых
коэффициентов перпендикулярных прямых: , которая используется в некоторых
задачах.
Решим Задачу 83 вторым способом, для этого перепишем прямые в нужном виде:
Таким образом, угловые коэффициенты: , и алгоритм похож:
1) Проверим, будут ли прямые перпендикулярны:
, значит, прямые не перпендикулярны.
2) Используем формулу:
Ответ:
И третий способ состоит нахождении угла между направляющими векторами прямых с помощью скалярного произведения: , но здесь не принимается во внимание ориентация угла (по любому получится
). Кроме того, он может оказаться тупым, и тогда придётся делать оговорку, что угол между
прямыми – это меньший угол, и из радиан (не из
!) вычитать получившийся арккосинус.
Какой способ выбрать? Ориентируйтесь на вашу задачу, методичку или ситуацию.
Задача 84
Найти угол между прямыми .
Самостоятельно, всеми тремя способами! Решение и ответ в конце книги.
И по просьбам учащихся ещё один пункт:


| Оглавление |
Автор: Aлeксaндр Eмeлин









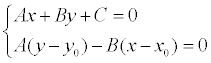


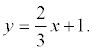




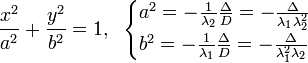


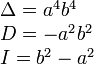
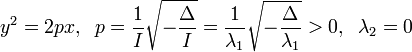






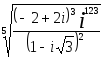 .
. .
. .
. .
. .
.