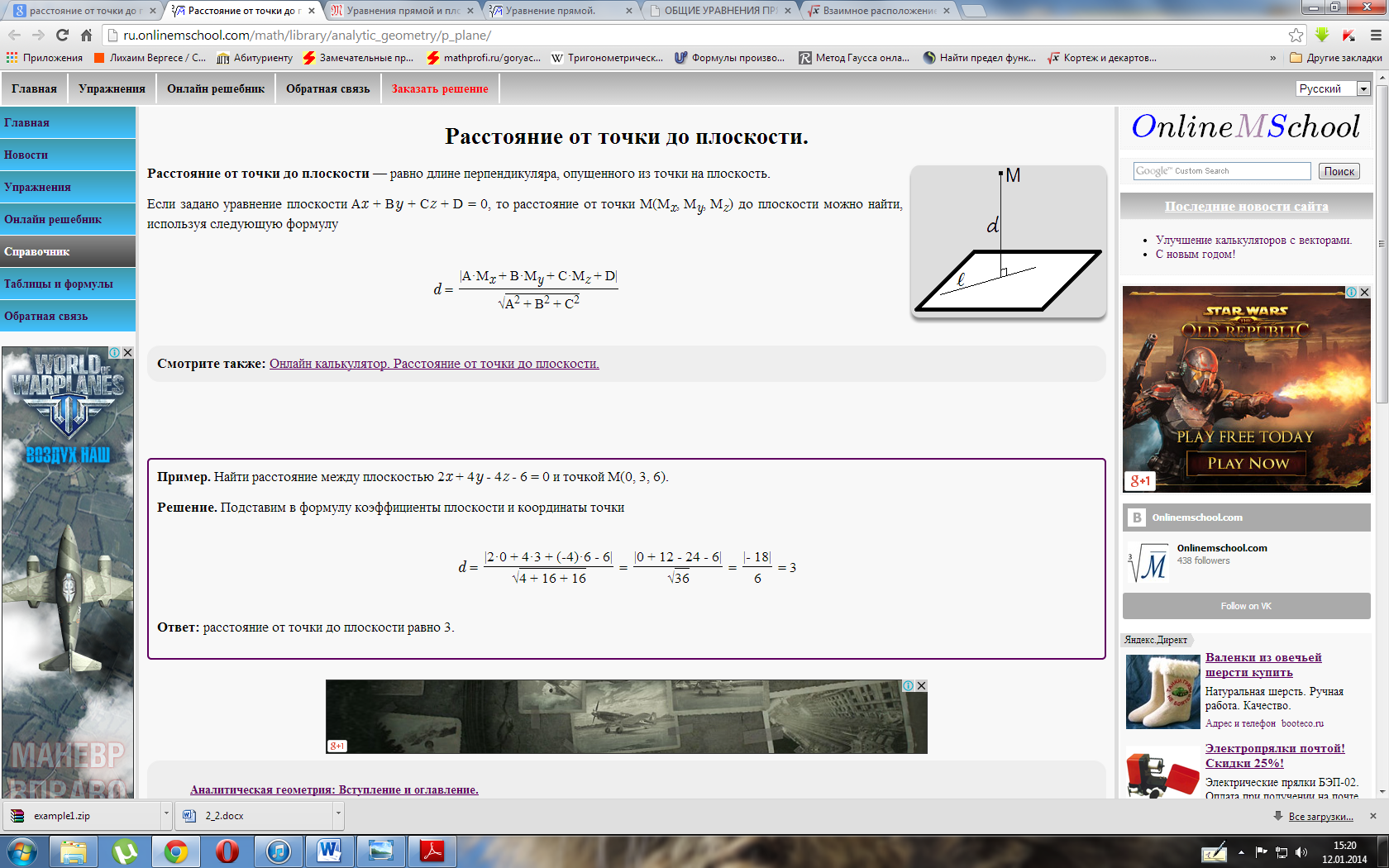
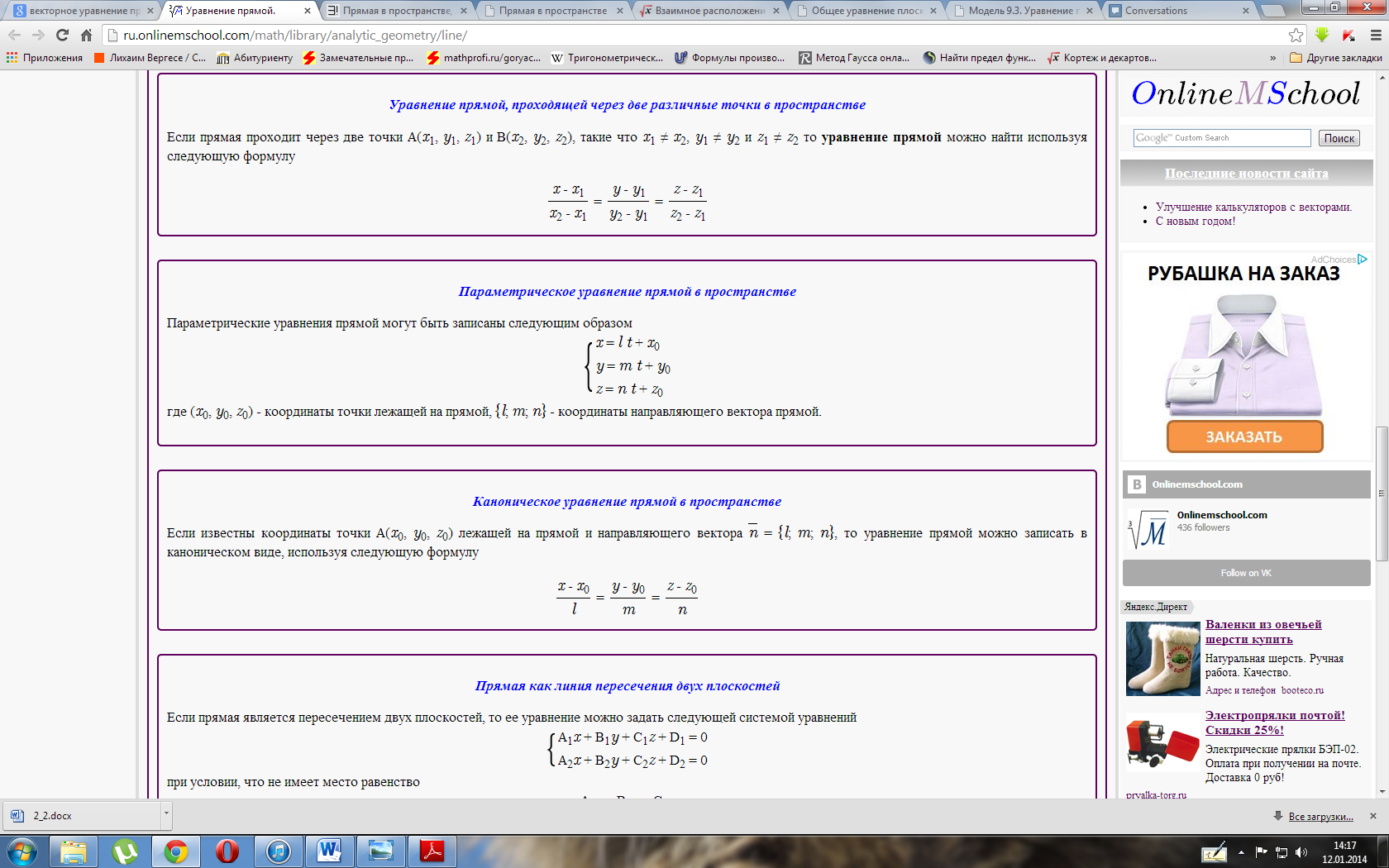
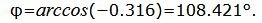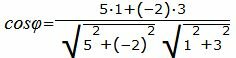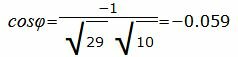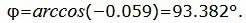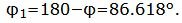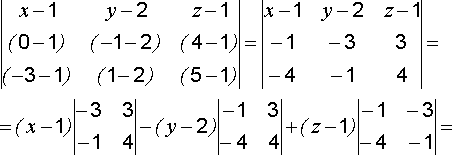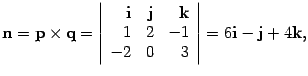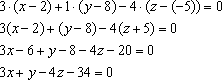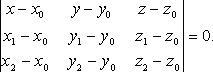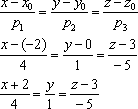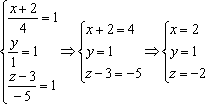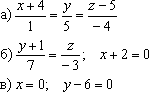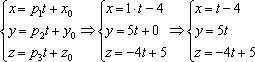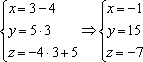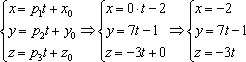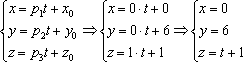Как найти угол между прямыми заданными параметрически - Исправление недочетов и поиск решений вместе с Examum.ru

Угол между прямыми онлайн

С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

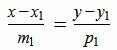(1.1)

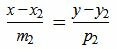(1.2)

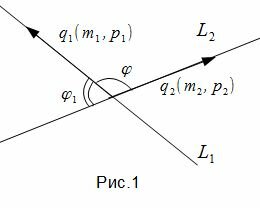
Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ (рис.1).

(1.3)

Из выражения (1.3) получим:

Таким образом, из формулы (1.4) можно найти угол между прямыми L₁ и L₂. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ₁. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

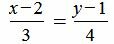(1.5)

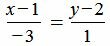(1.6)

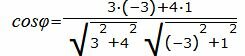
Упростим и решим:

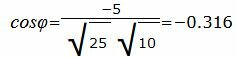
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

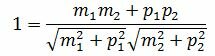(1.7)

Сделаем преобразования с выражением (1.7):

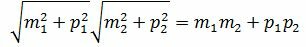
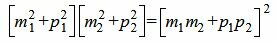
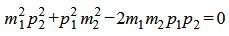
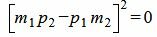
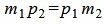(1.8)

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

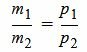(1.9)

Пример 2. Определить, параллельны ли прямые

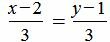(1.10)

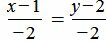(1.11)

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

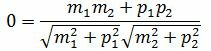(1.12)

Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

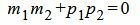(1.13)

Пример 3. Определить, перпендикулярны ли прямые

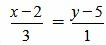(1.14)

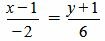(1.15)

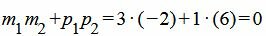(16)

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

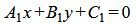(1.17)

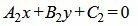(1.18)

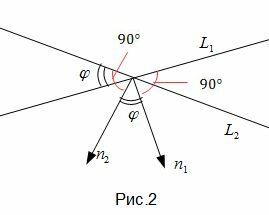
Так как нормальным вектором прямой L₁ является n₁=(A₁, B₁), а нормальным вектором прямой L₂ является n₂=(A₂, B₂), то задача об определении угла между прямыми L₁ и L₂ сводится к определению угла φ между векторами n₁ и n₂ (Рис.2).

Из определения скалярного произведения двух векторов, имеем:

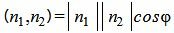(1.19)

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

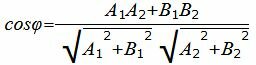(23)

Упростим и решим:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:

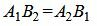(1.24)

С другой стороны условие параллельности прямых L₁ и L₂ эквивалентно условию коллинеарности векторов n₁ и n₂ и можно представить так:

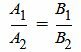(1.25)

Как видим уравнения (1.24) и (1.25) эквивалентны при A₂≠0 и B₂≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).

Пример 5. Определить, параллельны ли прямые

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Условие перпендикулярности прямых L₁ и L₂ можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n₁,n₂)=0. Откуда

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

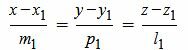(2.1)

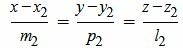(2.2)

Задача об определении угла между прямыми L₁ и L₂ сводится к задаче об определении угла между направляющими векторами q₁ и q₂ .

(2.3)

Из выражения (2.3) получим:

Таким образом, из формулы (2.4) можно найти угол между прямыми L₁ и L₂. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L₁ и L₂: φ₁=180-φ.

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

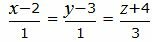(2.5)

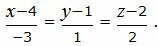(2.6)

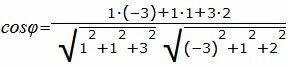
Упростим и решим:

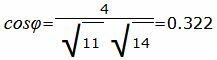
Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q₁ и q₂, т.е. соответствующие координаты этих векторов пропорциональны. Пусть

m₁=αm₂, p₁=αp₂, l₁=αl₂

(2.7)

где α − некоторое число. Тогда соответствующие координаты векторов q₁ и q₂ пропорциональны, и, следовательно прямые L₁ и L₂ параллельны.

Условие параллельности прямых можно представить и так:

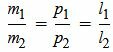(2.8)

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

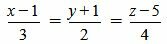(2.9)

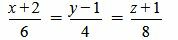(2.10)

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

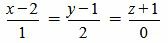(2.11)

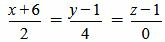(2.12)

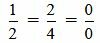(2.13)

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

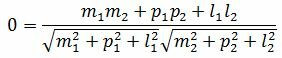(2.15)

Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L₁ и L₂ были перпендикулярны , должно выполняться условие

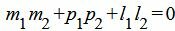(2.16)

Пример 3. Определить, перпендикулярны ли прямые

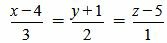(2.17)

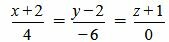(2.18)

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Угол между прямыми

Определение угла между прямыми

Угол между прямыми на плоскости

Угол между прямыми заданными уравнениями с угловым коэффициентом

то угол между ними можно найти, используя формулу:

Если знаменатель равен нулю (1 + k ₁· k ₂ = 0), то прямые перпендикулярны.

Соответственно легко найти угол между прямыми

tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k ₁ — k ₂ 1 + k ₁· k ₂

Угол между прямыми через направляющие векторы этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано параметрически

x = l t + a y = m t + b

то вектор направляющей имеет вид

Если уравнение прямой задано как

то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .

Если дано каноническое уравнение прямой

то вектор направляющей имеет вид

Если задано уравнение прямой с угловым коэффициентом

то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =

Угол между прямыми через векторы нормалей этих прямых

cos φ = | a · b | | a | · | b |

Если уравнение прямой задано как

то вектор нормали имеет вид

Если задано уравнение прямой с угловым коэффициентом

то вектор нормали имеет вид

Угол между прямыми через направляющий вектор и вектор нормали этих прямых

sin φ = | a · b | | a | · | b |

Примеры задач на вычисления угла между прямыми на плоскости

Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:

tg γ = k ₁ — k ₂ 1 + k ₁· k ₂ = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1

Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.

Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор

cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8

Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.

Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.

2 x + 3 y = 0 => y = — 2 3 x ( k ₁ = — 2 3 )

x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k ₂ = 4 3 )

tg γ = k ₁ — k ₂ 1 + k ₁· k ₂ = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18

Угол между прямыми в пространстве

cos φ = | a · b | | a | · | b |

Если дано каноническое уравнение прямой

то направляющий вектор имеет вид

Если уравнение прямой задано параметрически

x = l t + a y = m t + b z = n t + c

то направляющий вектор имеет вид

Решение: Так как прямые заданы параметрически, то <2; 1; -1>- направляющий вектор первой прямой, <1; -2; 0>направляющий вектор второй прямой.

cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0

Решение: Для решения этой задачи найдем направляющие векторы этих прямых.

Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.

Преобразуем второе уравнение к каноническому вид.

1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3

3 z — 5 2 = z — 5/3 2/3

Получено уравнение второй прямой в канонической форме

x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3

<-2; — 1 3 ; 2 3 >- направляющий вектор второй прямой.

cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205

Угол между прямыми в пространстве

Пусть в пространстве заданы прямые l и m. Через некоторую точку А пространства проведем прямые l₁ || l и m₁ || m (рис. 138).

Заметим, что точка А может быть выбрана произвольно, в частности она может лежать на одной из данных прямых. Если прямые l и m пересекаются, то за А можно взять точку пересечения этих прямых (l₁ = l и m₁ = m).

Углом между непараллельными прямыми l и m называется величина наименьшего из смежных углов, образованных пересекающимися прямыми l₁ и m₁ ( l₁ || l , m₁ || m). Угол между параллельными прямыми считается равным нулю.

Угол между прямыми l и m обозначается ( widehat <(l;m)>). Из определения следует, что если он измеряется в градусах, то 0° π /₂ .

Найти угол между прямыми АВ и DС₁.

Прямые АВ и DС₁ скрещивающиеся. Так как прямая DC параллельна прямой АВ, то угол между прямыми АВ и DС₁, согласно определению, равен (widehatDC>).

Следовательно, (widehat<(AB;DC_1)>) = 45°.

Прямые l и m называются перпендикулярными, если ( widehat <(l;m)>) = π /₂. Например, в кубе

(см. рис. 139) прямая A₁D₁перпендикулярна прямым DC, DC₁, СС₁ .

Вычисление угла между прямыми.

Задача вычисления угла между двумя прямыми в пространстве решается так же, как и на плоскости. Обозначим через φ величину угла между прямыми l₁ и l₂, а через ψ — величину угла между направляющими векторами а и b этих прямых.

ψ 90° (рис. 206,6), то φ = 180° — ψ. Очевидно, что в обоих случаях верно равенство cos φ = |cos ψ|. По формуле (косинус угла между ненулевыми векторами а и b равен скалярному произведению этих векторов, деленному на произведение их длин) имеем

Пусть прямые заданы своими каноническими уравнениями

Тогда угол φ между прямыми определяется с помощью формулы

Если одна из прямых (или обе) задана не каноничecкими уравнениями, то для вычисления угла нужно найти координаты направляющих векторов этих прямых, а затем воспользоваться формулой (1).

Задача 1. Вычислить угол между прямыми

Направляющие векторы прямых имеют координаты:

По формуле (1) находим

Следовательно, угол между данными прямыми равен 60°.

Задача 2. Вычислить угол между прямыми

За направляющий вектор а первой прямой возьмем векторное произведение нормальных векторов n₁ = (3; 0; -12) и n₂ = (1; 1; -3) плоскостей, задающих эту прямую. По формуле ( [a; b]=begin i & j & k \ x_1 & y_1 & z_1 \ x_2 & y_2 & z_2 end ) получаем

$$ a=[n_1; n_2]=begin i & j & k \ 3 & 0 & -12 \ 1 & 1 & -3 end=12i-3i+3k $$

Аналогично находим направляющий вектор второй прямой:

$$ b=begin i & j & k \ 4 & -1 & 1 \ 0 & 1 & 1 end=-2i-4i+4k $$

Но формуле (1) вычисляем косинус искомого угла:

Следовательно, угол между данными прямыми равен 90°.

Задача 3. В треугольной пирамиде МАВС ребра MA, MB и МС взаимно перпендикулярны, (рис. 207);

их длины соответственно равны 4, 3, 6. Точка D — середина [МА]. Найти угол φ между прямыми СА и DB.

Пусть СА и DB — направляющие векторы прямых СА и DB.

Примем точку М за начало координат. По условию зядачи имеем А (4; 0; 0), В(0; 0; 3), С(0; 6; 0), D (2; 0; 0). Поэтому (overrightarrow) = (4; — 6;0), (overrightarrow)= (-2; 0; 3). Воспользуемся формулой (1):

По таблице косинусов находим, что угол между прямыми СА и DB равен приблизительно 72°.

источники:

http://ru.onlinemschool.com/math/library/analytic_geometry/lines_angle/

http://razdupli.ru/teor/84_ugol-mezhdu-pryamymi-v-prostranstve.php

Источник

Угол между прямыми онлайн

1. Угол между прямыми на плоскости

Прямые заданы каноническими уравнениями

1.1. Определение угла между прямыми

Пусть в двухмерном пространстве прямые L₁ и L₂ заданы каноническими уравнениями

где q₁=(m₁, p₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂) направляющий вектор прямой L₂.

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (1.3) получим:

Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Решение. Прямая (1.5) имеет направляющий вектор q₁=(m₁, p₁)=(3, 4), а прямая (1.6) − q₂=(m₂, p₂)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m₁, p₁, m₂, p₂ в (1.4):

Упростим и решим:

Найдем угол φ

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

Ответ.

Угол между прямыми равен:

1.2. Условие параллельности прямых

Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:

Сделаем преобразования с выражением (1.7):

Таким образом условие параллельности прямых L₁ и L₂ имеет вид (1.8). Если m₂≠0 и p₂≠0, то (1.8) можно записать так:

Пример 2. Определить, параллельны ли прямые

Решение. Прямая (1.10) имеет направляющий вектор q₁=(m₁, p₁)=(3, 3), а прямая (1.11) − q₂=(m₂, p₂)=(−2, −2). Тогда

Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.

Ответ. Прямые (1.10) и (1.11) параллельны.

1.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:

Пример 3. Определить, перпендикулярны ли прямые

Решение. Прямая (1.14) имеет направляющий вектор q₁=(m₁, p₁)=(3, 1), а прямая (1.15) − q₂=(m₂, p₂)=(−2, 6). Тогда

Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.

Ответ. Прямые (1.14) и (1.15) перпендикулярны.

Прямые заданы общими уравнениями

1.4. Определение угла между прямыми

Пусть две прямые L₁ и L₂ заданы общими уравнениями

Из определения скалярного произведения двух векторов, имеем:

где |n₁| и |n₂| модули нормальных векторов n₁ и n₂ соответственно, φ -угол между векторами n₁ и n₂.

Из уравнения (19) получим

Пример 4. Найти угол между прямыми

Решение. Прямая (1.21) имеет нормальный вектор n₁=(A₁, B₁)=(5, −2), а прямая (1.22) − n₂=(A₂, B₂)=(1, 3). Задача определения угла между прямыми L₁ и L₂ сводится к определению угла между векторами n₁ и n₂. Из определения скалярного произведения векторов имеем: (n₁,n₂)=|n₁||n₂|cosφ. Тогда

Подставляя значения A₁, B₁, A₂, B₂ в (1.23), получим:

Упростим и решим:

Найдем угол φ:

Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:

1.5. Условие параллельности прямых

Пример 5. Определить, параллельны ли прямые

Решение. Прямая (1.26) имеет нормальный вектор n₁=(A₁, B₁)=(4, 2), а прямая (1.27) − n₂=(A₂, B₂)=(2, 1). Тогда подставляя значения A₁, B₁, A₂, B₂ в (1.24), получим

Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.

Ответ. Прямые (1.26) и (1.27) параллельны.

1.6. Условие перпендикулярности прямых

Таким образом условие перпендикулярности прямых определяется равенством (1.28).

Пример 6. Определить, перпендикулярны ли прямые

Решение. Прямая (1.29) имеет нормальный вектор n₁=(A₁, B₁)=(4, −1), а прямая (1.30) − n₂=(A₂, B₂)=(2, 8). Тогда подставляя значения A₁, B₁, A₂, B₂ в (28), получим

Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.

Ответ. Прямые (1.29) и (1.30) перпендикулярны.

2. Угол между прямыми в пространстве

2.1. Определение угла между прямыми

Пусть в пространстве прямые L₁ и L₂ заданы каноническими уравнениями

где q₁=(m₁, p₁, l₁) направляющий вектор прямой L₁, а q₂=(m₂, p₂, l₂) направляющий вектор прямой L₂.

Из определения скалярного произведения:

где |q₁| и |q₂| модули направляющих векторов q₁ и q₂ соответственно, φ -угол между векторами q₁ и q₂.

Из выражения (2.3) получим:

Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.

Пример 1. Определить угол между прямыми

Решение. Прямая (2.5) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 1, 3), а прямая (2.6) − q₂=(m₂, p₂, l₂)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.4):

Упростим и решим:

Найдем угол φ

Ответ.

Угол между прямыми равен:

2.2. Условие параллельности прямых

Условие параллельности прямых можно представить и так:

Отметим, что любую пропорцию нужно понимать как равенство ad=bc.

Пример 2. Определить, параллельны ли прямые

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 4), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(6, 4, 8). Тогда

Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.

Ответ. Прямые (2,9) и (2,10) параллельны.

Пример 3. Определить, параллельны ли прямые

Решение. Прямая (2.9) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(1, 2, 0), а прямая (2.10) − q₂=(m₂, p₂, l₂)=(2, 4, 0). Подставляя значения m₁, p₁, l₁, m₂, p₂, l₂ в (2.8), получим

Выражение (2.13) нужно понимать так:

Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.

Ответ. Прямые (2.11) и (2.12) параллельны.

2.3. Условие перпендикулярности прямых

Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:

Пример 3. Определить, перпендикулярны ли прямые

Решение. Прямая (2.16) имеет направляющий вектор q₁=(m₁, p₁, l₁)=(3, 2, 1), а прямая (2.17) − q₂=(m₂, p₂, l₂)=(4, −6, 0). Тогда

Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.

Ответ. Прямые (2.17) и (2.18) перпендикулярны.

Источник

Параметрические уравнения прямой.

Описание прямой с помощью параметрических уравнений является еще одним подходом к ее исследованию. Им пользуются довольно часто в механике, где параметр t выступает как время.

Пусть в заданной декартовой прямоугольной системе координат Oхy известна точка (рис. 4.6),

Рис. 4.6. Задание прямой с помощью параметрических уравнений.

Через которую проходит прямая, и дан ненулевой вектор , ей параллельный, который будем называть направляющим вектором.

Рассмотрим произвольную точку , лежащую на прямой, и введем, как и ранее, радиусы-векторы:

Тогда вектор

Для точек прямой и только для них будет коллинеарен направляющему вектору

А потому

Где t – числовой параметр, который для каждой определенной точки M, лежащей на прямой, принимает конкретное значение. Переписав это уравнение в виде

(4.21)

Получим ВЕКТОРНО-ПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕ ПРЯМОЙ. Проектируя вектор (4.21) на координатные оси, найдем координатно-параметрические уравнения прямой:

(4.22)

Могут ли параметрические уравнения не быть линейными относительно параметра t?

В данном случае прямая определяется двумя уравнениями. Задавая конкретные значения t, мы можем вычислить абсциссу и ординату точки прямой.

Выразим из этих уравнений параметр t:

И приравняем правые части полученных равенств:

(4.23)

Это есть каноническое уравнение прямой, где x0 и y0 – координаты известной точки, лежащей на прямой, l и m – координаты направляющего вектора.

Какая-либо из координат этого вектора может обращаться в ноль. Тогда каноническое уравнение имеет символический смысл, так как деление на ноль невозможно.

Рис. 4.7. Нахождение угла между прямыми, заданными параметрически.

Параметрические и каноническое уравнения позволяют достаточно просто определить взаимное расположение прямых путем использования соответствующих направляющих векторов. Если этими векторами являются и (рис. 4.7), то

, (4.24)

Или в координатной форме:

(4.25)

< Предыдущая		Следующая >

Источник

Под углом между этими прямыми понимают
угол между их направляющими векторами
S₁=(m₁;n₁;p₁)
иS₂=(m₂;n₂;p₂).
Тогда, по формуле для косинуса угла
между векторами, получаемили.

Пример: Заданы прямые l₁:иl₂:
;
S₁=(m₁;n₁;p₁)=(1;-0,5;1)
иS₂=(m₂;n₂;p₂)=(1;-9;-6).

Подставляем наши значения в формулу:
.

Для нахождения острого угла между
прямыми числитель правой части формулы
следует взять по модулю.

Если прямые перпендикулярны, то в этом
и только в этом случае имеем
.
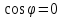
Следовательно, числитель дроби равен
нулю, т. е.,
так как | S₁|и | S₂|.

Если прямые параллельны, то параллельны
их направляющие векторы. Следовательно,
координаты этих векторов пропорциональны,
т. е.
.

38.Угол
между прямой на плоскости и плоскостью
в пространстве. Условия параллельности
и перпендикулярности их в пространстве.

Углом между прямой и плоскостью
называется любой из двух смежных углов,
образованных прямой и её проекцией на
плоскость. Обозначим через
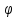
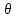
угол между плоскостьюQи прямойl, а через— угол между векторами=(A;B;C)
и.
Тогда.
При этом:
если,
то;
если,
то.

Пример: Даны плоскость Q:
x+3y+5z-42=0
и прямаяL:
.

Острый угол между плоскостью и прямой
можно найти, взяв в формуле модуль правой
части.

Если прямая l
параллельна плоскости Q,
то векторыиперпендикулярны, а потому,
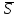
т. е.–условие параллельности прямой и
плоскости.

Если прямая L
перпендикулярна плоскости Q,
то векторыипараллельны. Поэтому равенства–условие перпендикулярности прямой
и плоскости.

Пересечение
прямой с плоскостью. Условие принадлежности
прямой плоскости.

Чтобы найти точку пересечения прямой
и плоскости нужно решить систему,
состоящую из уравнений прямой и плоскости.
Проще всего это сделать, записав уравнения
прямой в параметрическом виде: l:.

Подставляя эти выражения для x,
yи zв уравнение плоскости, получаем уравнениеили;,
и приведя подобные, мы получаем значение,
но при условии, что прямая не параллельна
плоскости, т. е..

Пример: Требуется найти точку пересечения
прямой l:
с плоскостьюQ:
x+3y+5z-42=0.

Подставляя найденное значение параметра
в параметрические уравнения прямой,
найдем координаты точки пересечения
прямой с плоскостью:,
т. е. точкаО(4;1;7) – точка пересечения
прямойlс плоскостьюQ.

Рассмотрим случай, когда
:

А) если
,
то прямая параллельна плоскости и
пересекать ее не будет, т. е. уравнениерешения не имеет.

Б) если
,
то уравнениюудовлетворяет любое значение,
любая точка прямой является точкой
пересечения прямой и плоскости.
Следовательно, прямая лежит на плоскости.

Таким образом, одновременное выполнение
равенств
являетсяусловием принадлежности
прямой плоскости.

Соседние файлы в папке 1семестр_ответы

Источник

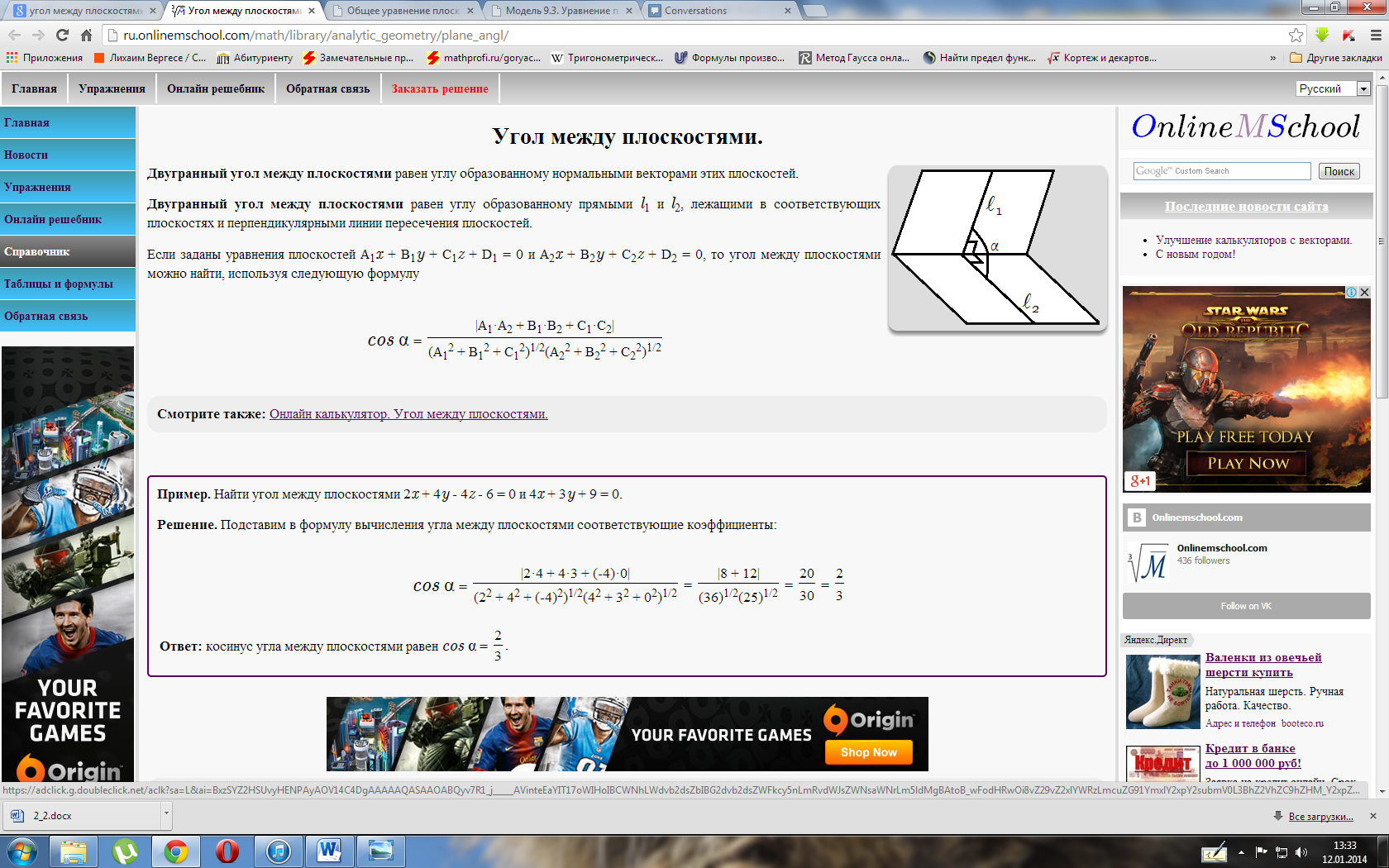
Угол между двумя прямыми

Угол φ между
двумя прямыми, заданными общими
уравнениями A₁x
+ B₁y
+ C₁ =
0 и A₂x
+ B₂y
+ C₂ =
0, вычисляется по формуле:

Угол φ между
двумя прямыми, заданными каноническими
уравнениями (x-x₁)/m₁ =
(y-y₁)/n₁ и
(x-x₂)/m₂ =
(y-y₂)/n₂,
вычисляется по формуле:

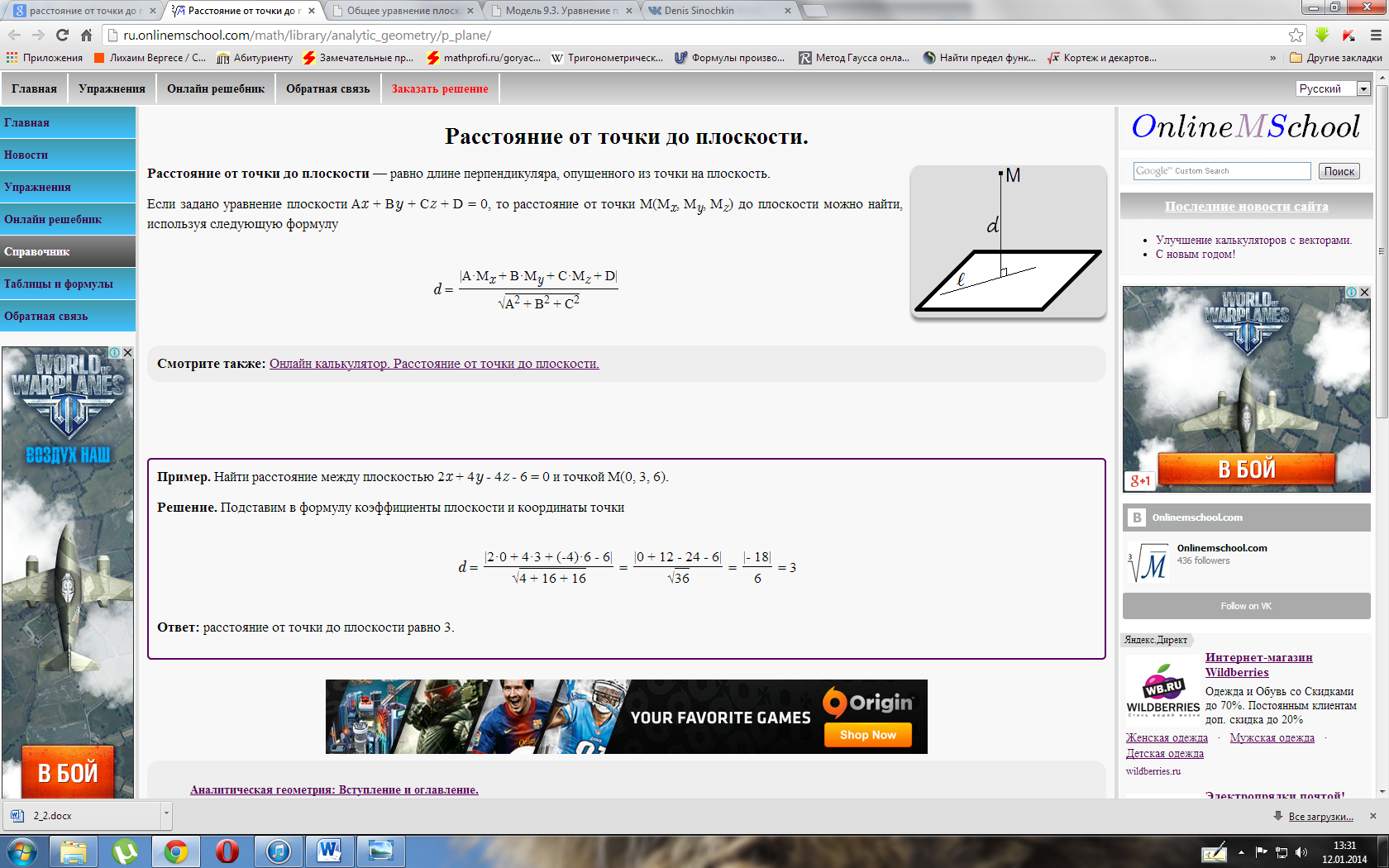
Расстояние от точки до прямой

3,2

Каждую
плоскость в пространстве можно представить
как линейное уравнение, называемое общим
уравнением плоскости

Частные
случаи.

o Если
в уравнении (8) ,
то плоскость проходит через начало
координат.

o При (,)
плоскость параллельна оси(оси,
оси)
соответственно.

o При (,) плоскость
параллельна плоскости(плоскости,
плоскости).

Решение:
используем (7)

Ответ:
общее уравнение плоскости .

Пример.

Плоскость
в прямоугольной системе координат Oxyz задана
общим уравнением плоскости .
Запишите координаты всех нормальных
векторов этой плоскости.

Решение.

Нам
известно, что коэффициенты при
переменных x, y и z в общем
уравнении плоскости являются
соответствующими координатами нормального
вектора этой плоскости. Следовательно,
нормальный вектор заданной
плоскостиимеет
координаты.
Множество всех нормальных векторов
можно задать как.

Ответ:

Пример.

Напишите
уравнение плоскости, если в прямоугольной
системе координат Oxyz в пространстве
она проходит через точку ,
а—
нормальный вектор этой плоскости.

Решение.

Приведем
два решения этой задачи.

Из
условия имеем .
Подставляем эти данные в общее уравнение
плоскости, проходящей через точку:

Пример.

Напишите
общее уравнение плоскости параллельной
координатной плоскости Oyz и
проходящей через точку .

Решение.

Плоскость,
которая параллельна координатной
плоскости Oyz, может быть задана общим
неполным уравнением плоскости вида .
Так как точкапринадлежит
плоскости по условию, то координаты
этой точки должны удовлетворять уравнению
плоскости,
то есть, должно быть справедливо
равенство.
Отсюда находим.
Таким образом, искомое уравнение имеет
вид.

Решение. Векторное
произведение по определению
10.26 ортогонально
векторам p и q.
Следовательно, оно ортогонально искомой
плоскости и вектор можно
взять в качестве ее нормального вектора.
Найдем координаты вектора n:

то
есть .
Используя формулу (11.1),
получим

Раскрыв
в этом уравнении скобки, приходим к
окончательному ответу.

Ответ: .

Найти
единичный нормальный вектор плоскости .

Перепишем
вектор нормали в виде и
найдём его длину:

Согласно
вышесказанному:

Ответ:

Построить
плоскость, проходящую через
точку параллельно
плоскости .

У
параллельных плоскостей один и тот же
вектор нормали. 1) Из уравнения найдём
вектор нормали плоскости:.

2)
Уравнение плоскости составим
по точкеи
вектору нормали:

Ответ:

Векторное
уравнение плоскости в пространстве

Параметрическое
уравнение плоскости в пространстве

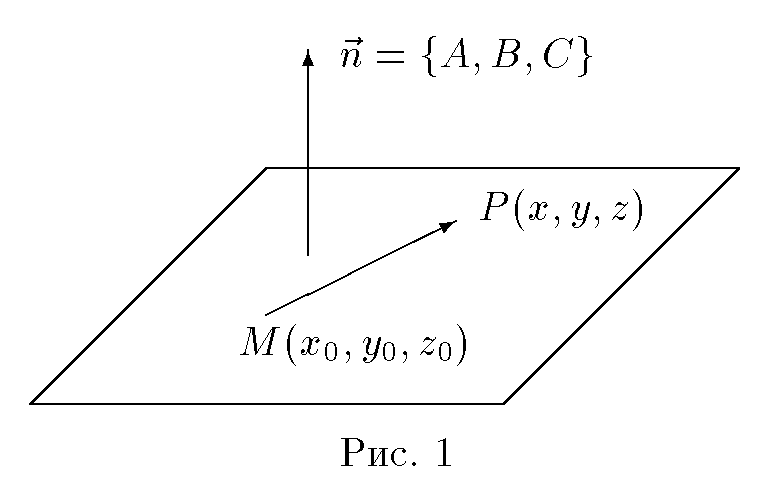
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору

Пусть
в трехмерном пространстве задана
прямоугольная декартова система
координат. Сформулируем следующую
задачу:

Составить
уравнение плоскости, проходящей через
данную точку
M(x0,
y0,
z0) перпендикулярно
данному вектору
n =
{A, B, C}
.

Решение. Пусть P(x, y, z)
— произвольная точка пространства.
Точка P принадлежит
плоскости тогда и только тогда, когда
вектор
MP =
{x − x0, y − y0, z − z0}
ортогонален вектору n =
{A, B, C}
(рис.1).

Написав
условие ортогональности этих векторов
(n, MP)
= 0 в координатной форме, получим:

A(x − x0)
+ B(y − y0)
+ C(z − z0)
= 0

Уравнение
плоскости по трем точкам

В
векторном виде

В
координатах

Взаимное
расположение плоскостей в пространстве

Пусть

– общие уравнения двух
плоскостей. Тогда:

1)
если ,
то плоскости совпадают;

2)
если ,
то плоскости параллельны;

3)
если или ,
то плоскости пересекаются и системауравнений

(6)

является
уравнениями прямой пересечения данных
плоскостей.

3.3

Составить
канонические уравнения прямой по
точке и
направляющему вектору

Решение:
Канонические уравнения прямой составим
по формуле:

Ответ:

В
ряде задач требуется найти какую-нибудь
другую точку ,
принадлежащую данной прямой. Как это
сделать?

Берём
полученные уравнения и
мысленно «отщипываем», например, левый
кусочек: .
Теперь этот кусочек приравниваем к
любому числу (помним,
что ноль уже был), например, к единице: .
Так как ,
то и два других «куска» тоже должны
быть равны единице. По сути, нужно
решить систему:

Составить
параметрические уравнения следующих
прямых:

Решение:
Прямые заданы каноническими уравнениями
и на первом этапе следует найти
какую-нибудь точку, принадлежащую
прямой, и её направляющий вектор.

а)
Из уравнений снимаем
точку и направляющий вектор: .
Точку можно выбрать и другую (как это
сделать – рассказано выше), но лучше
взять самую очевидную. Кстати, во
избежание ошибок, всегда подставляйте
её координаты в уравнения.

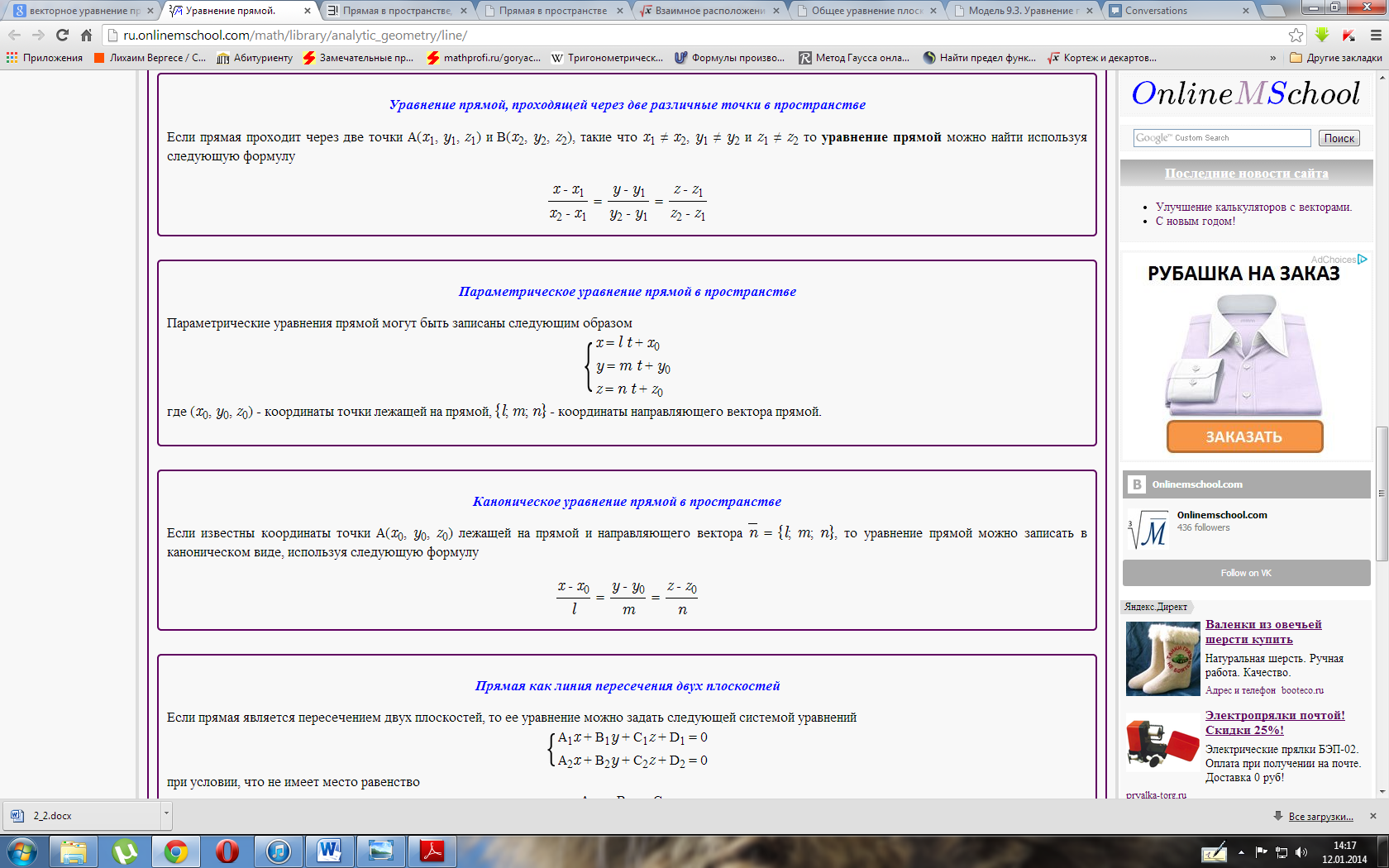
Составим
параметрические уравнения данной
прямой:

Удобство
параметрических уравнений состоит в
том, что с их помощью очень легко находить
другие точки прямой. Например, найдём
точку ,
координаты которой, скажем, соответствуют
значению параметра :

Таким
образом:

б)
Рассмотрим канонические уравнения .
Выбор точки здесь несложен, но
коварен: (будьте
внимательны, не перепутайте координаты!!!).
Как вытащить направляющий вектор? Можно
порассуждать, чему параллельна данная
прямая, а можно использовать простой
формальный приём: в пропорции находятся
«игрек» и «зет», поэтому запишем
направляющий вектор ,
а на оставшееся место поставим ноль: .

Составим
параметрические уравнения прямой:

в)
Перепишем уравнения  в
виде ,
то есть «зет» может быть любым. А если
любым, то пусть, например, .
Таким образом, точка  принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях  находятся
«икс» и «игрек», и в направляющем векторе
на данных местах записываем нули: .
На оставшееся место ставим единицу: .
Вместо единицы подойдёт любое число,
кроме нуля.

Запишем
параметрические уравнения прямой:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник