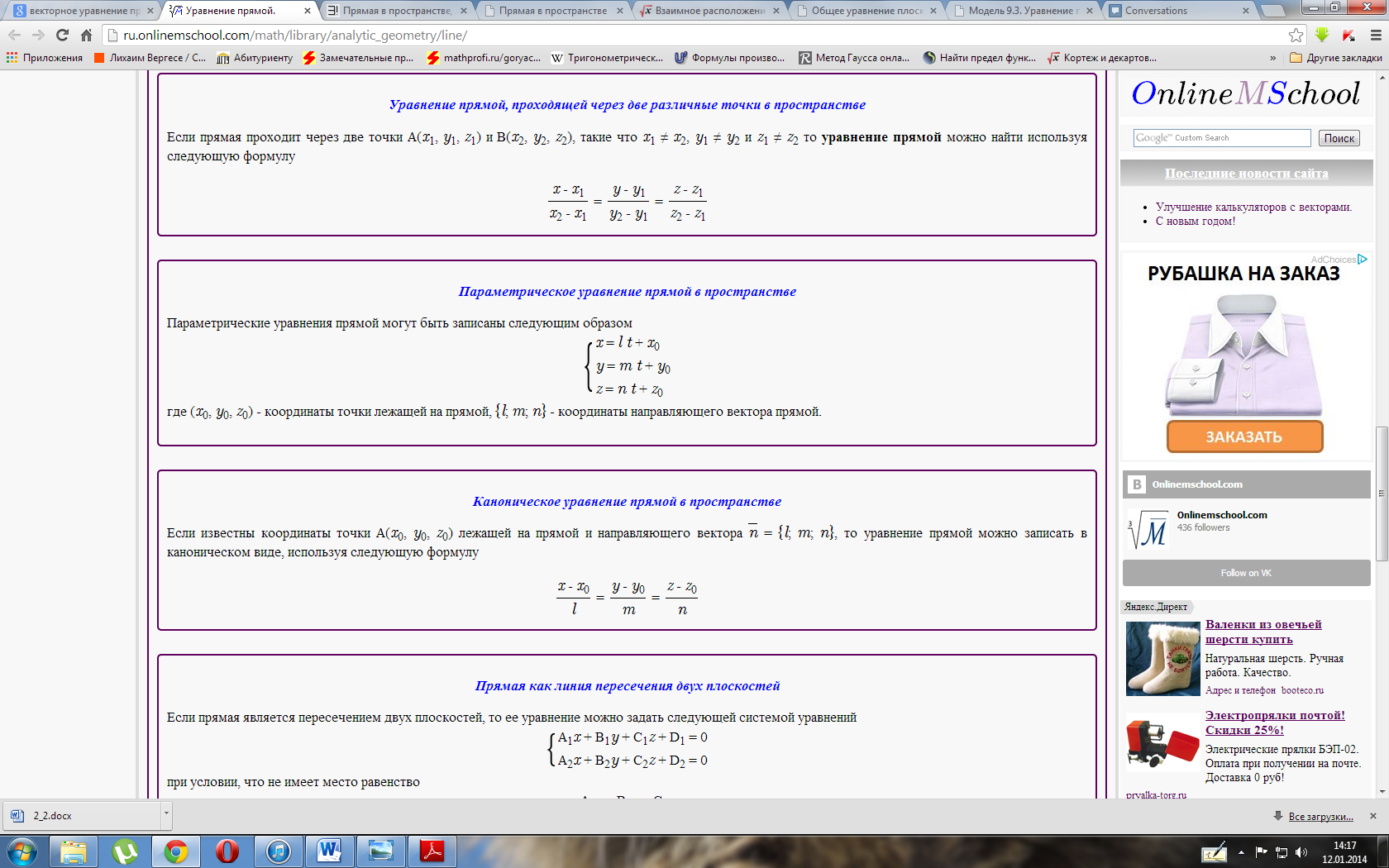
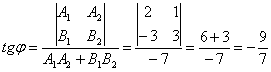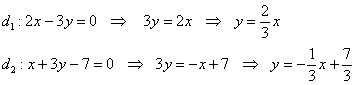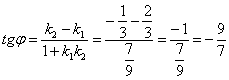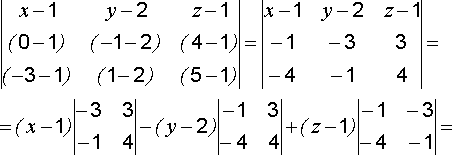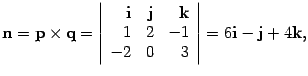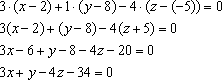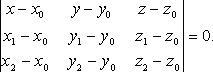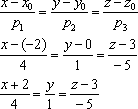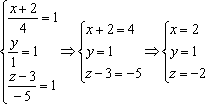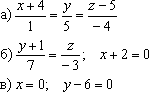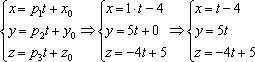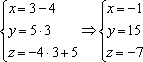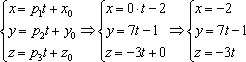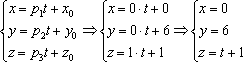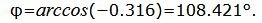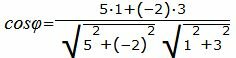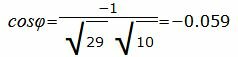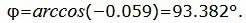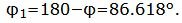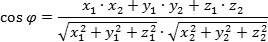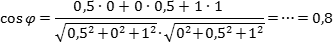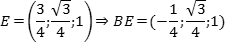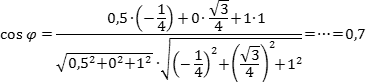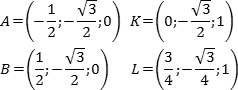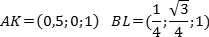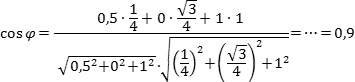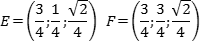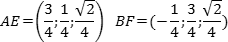Определение угла между прямыми
Две прямые называются пересекающимися, если они имеют единственную общую точку. Эта точка называется точкой пересечения прямых. Прямые разбиваются точкой пересечения на лучи, которые образуют четыре неразвернутых угла, среди которых две пары вертикальных углов и четыре пары смежных углов. Если известен размер одного из углов, образованных пересекающимися прямыми, то легко определить размер остальных углов. Если один из углов прямой, то все остальные тоже прямые, а прямые перпендикулярны.
Определение Угол между прямыми — размер наименьшего из углов, образованных этими прямыми.
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
Если две прямые заданы уравнениями с угловым коэффициентом
y = k1x + b1,
y = k2x + b2,
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k1·k2 = 0), то прямые перпендикулярны.
Доказательство. Если прямые заданы уравнениями с угловыми коэффициентами, то легко найти углы между этими прямыми и осью OX
tg α = k1
tg β = k2
Соответственно легко найти угол между прямыми
γ = α — β
tg γ = tg (α — β) = tg α — tg β1 + tg α ·tg β = k1 — k21 + k1·k2
Угол между прямыми через направляющие векторы этих прямых
Если a — направляющий вектор первой прямой и b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
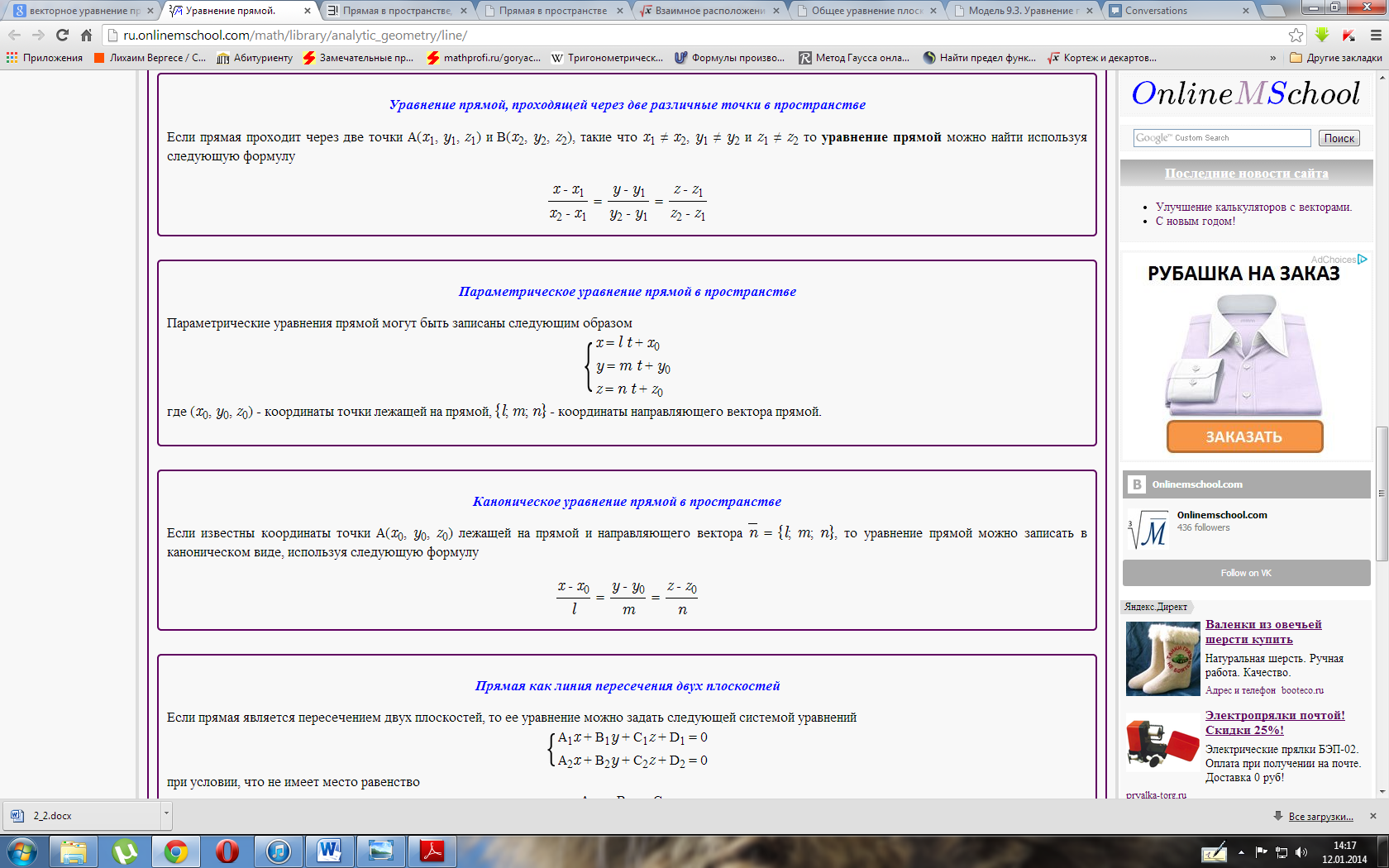
Если уравнение прямой задано параметрически
x = l t + ay = m t + b
то вектор направляющей имеет вид {l; m}
Если уравнение прямой задано как
A x + B y + C = 0
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = -CB значит точка на прямой имеет координаты K(0, -CB), при y = 0 => x = -CA значит точка на прямой имеет координаты M(-CA, 0). Вектор направляющей KM = {-CA; CB}.
Если дано каноническое уравнение прямой
x — x0 l = y — y0m
то вектор направляющей имеет вид {l; m}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b). Вектор направляющей KM = {1; k}
Угол между прямыми через векторы нормалей этих прямых
Если a — вектор нормали первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если уравнение прямой задано как
A x + B y + C = 0
то вектор нормали имеет вид {A; B}
Если задано уравнение прямой с угловым коэффициентом
y = kx + b
то вектор нормали имеет вид {1; —k}
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
Если a — направляющий вектор первой прямой и b — вектор нормали второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
sin φ = |a · b||a| · |b|
Примеры задач на вычисления угла между прямыми на плоскости
Пример 1. Найти угол между прямыми y = 2x — 1 и y = -3x + 1.
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ =
k1 — k21 + k1·k2
=
2 — (-3)1 + 2·(-3)
=
5-5
= 1
Ответ. γ = 45°
Пример 2. Найти угол между прямыми y = 2x — 1 и x = 2t + 1y = t.
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор {1; 2}, для второй прямой направляющий вектор {2; 1}
cos φ =
|1 · 2 + 2 · 1|12 + 22 · 22 + 12
=
45 · 5
= 0.8
Ответ. φ ≈ 36.87°
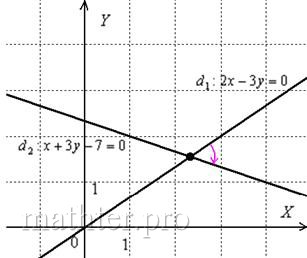
Пример 3 Найти угол между прямыми 2x + 3y = 0 и
x — 23
=
y4
.
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2x + 3y = 0 => y = -23x (k1 = -23)
x — 23 = y4 => y = 43x — 83 (k2 = 43)
tg γ =
k1 — k21 + k1·k2
=
-23 — 431 + (-23)·43
=
-631 — 89
= 18
Ответ. γ ≈ 86.82°
Угол между прямыми в пространстве
Если a — направляющий вектор первой прямой, а b — направляющий вектор второй прямой, то, используя скалярное произведение векторов, легко найти угол между прямыми:
cos φ = |a · b||a| · |b|
Если дано каноническое уравнение прямой
x — x0 l = y — y0m = z — z0n
то направляющий вектор имеет вид {l; m; n}
Если уравнение прямой задано параметрически
x = l t + ay = m t + bz = n t + c
то направляющий вектор имеет вид {l; m; n}
Пример 4. Найти угол между прямыми
x = 2t + 1y = tz = -t — 1
и
x = t + 2y = -2t + 1z = 1
.
Решение: Так как прямые заданы параметрически, то {2; 1; -1} — направляющий вектор первой прямой, {1; -2; 0} направляющий вектор второй прямой.
cos φ =
|2 · 1 + 1 · (-2) + (-1) · 0|22 + 12 + (-1)2 · 12 + (-2)2 + 02
=
06 · 5
= 0
Ответ. φ = 90°
Пример 5 Найти угол между прямыми
x — 23
=
y4
=
z — 35
и —
x — 22
= 1 — 3y =
3z — 52
.
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор {3; 4; 5}.
Преобразуем второе уравнение к каноническому вид.
—x — 22 = x — 2-2
1 — 3y = 1 + y-1/3 = y — 1/3-1/3
3z — 52 = z — 5/32/3
Получено уравнение второй прямой в канонической форме
x — 2-2 = y — 1/3-1/3 = z — 5/32/3
{-2; -13; 23} — направляющий вектор второй прямой.
cos φ =
3·(-2) + 4·(-13) + 5·2332 + 42 + 52 · (-2)2 + (-13)2 + (23)2
=
-6 — 43 + 1039 + 16 + 25 · 4 + 19 + 49
=
-450 · 41/9
=
12582
=
682205
Ответ. φ ≈ 74.63°
2.5.7. Как найти угол между прямыми?
Новая картинка за очередным поворотом:
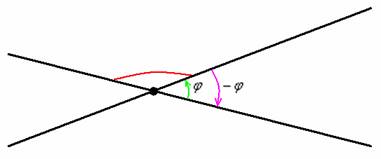
МЕНЬШИЙ угол, из чего автоматически следует, что он не может быть тупым. На рисунке угол, обозначенный красной дугой, не считается углом
между пересекающимися прямыми. А считается таковым его «зелёный» сосед или
отрицательно ориентированный «малиновый» угол . Если прямые
перпендикулярны, то за угол между ними можно принять любой из 4 углов.
…что-то не понятно? Срочно изучаем Приложение Тригонометрия!
Однако ещё раз: чем отличаются углы ? Ориентацией (направлением «прокрутки» угла).
Напоминаю, что отрицательно ориентированный угол «прокручивается» по часовой стрелке и записывается со знаком «минус».
Следует отметить, что ориентацию угла часто не принимают во внимание, и рассматривают «просто угол», который .
Как найти угол между двумя прямыми? Существуют три основные формулы.
Способ первый. Рассмотрим две прямые, заданные общими уравнениями в декартовой системе
координат:
Если , то прямые перпендикулярны (
либо
).
Если , то прямые не перпендикулярны и ориентированный угол
между ними можно вычислить с помощью
формулы:
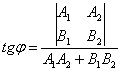
Знаменатель этой формулы – в точности, скалярное произведение направляющих векторов: ,
которое равно нулю тогда и только тогда, когда векторы ортогональны. …надеюсь, не забыли.
Задача 83
Найти угол между прямыми , заданными в декартовой системе координат.
Исходя из вышесказанного, решение удобно оформить в два шага:
1) Вычислим произведение:
, значит, прямые не перпендикулярны.
2) Угол между прямыми найдём с помощью формулы:
И с помощью обратной функции (см. Приложение Тригонометрия) легко найти сам угол, при этом используем нечётность арктангенса:
Ответ:
В ответе указываем точное значение, а также приближённое значение (желательно и в градусах, и в радианах), вычисленное с помощью
калькулятора.
Ну, минус, так минус, ничего страшного, вот геометрическая иллюстрация:
Неудивительно, что угол получился отрицательной ориентации, ведь в условии задачи «первым номером» идёт прямая и «открутка» угла началась именно с неё. Если очень хочется получить положительное значение, то нужно
поменять прямые местами, то есть коэффициенты взять из второго уравнения
, а коэффициенты
– из первого уравнения
. Короче
говоря, начать нужно
с прямой .
Скрывать не буду, сам подбираю прямые в том порядке, чтобы угол получился положительным. Так красивее, но не более того.
Способ второй, он удобен, когда прямые заданы уравнениями с
угловым коэффициентом: (в декартовых координатах).
Если , то прямые перпендикулярны (
либо
).
Если , то ориентированный угол
между ними можно найти с помощью формулы:
, и на самом деле это частный случай предыдущей формулы.
К слову, из равенства следует полезная взаимосвязь угловых
коэффициентов перпендикулярных прямых: , которая используется в некоторых
задачах.
Решим Задачу 83 вторым способом, для этого перепишем прямые в нужном виде:
Таким образом, угловые коэффициенты: , и алгоритм похож:
1) Проверим, будут ли прямые перпендикулярны:
, значит, прямые не перпендикулярны.
2) Используем формулу:
Ответ:
И третий способ состоит нахождении угла между направляющими векторами прямых с помощью скалярного произведения: , но здесь не принимается во внимание ориентация угла (по любому получится
). Кроме того, он может оказаться тупым, и тогда придётся делать оговорку, что угол между
прямыми – это меньший угол, и из радиан (не из
!) вычитать получившийся арккосинус.
Какой способ выбрать? Ориентируйтесь на вашу задачу, методичку или ситуацию.
Задача 84
Найти угол между прямыми .
Самостоятельно, всеми тремя способами! Решение и ответ в конце книги.
И по просьбам учащихся ещё один пункт:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
и
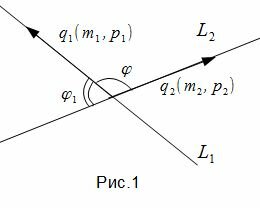
где q1=(m1, p1) направляющий вектор прямой L1, а q2=(m2, p2) направляющий вектор прямой L2.
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
Из определения скалярного произведения:
где |q1| и |q2| модули направляющих векторов q1 и q2 соответственно, φ -угол между векторами q1 и q2.
Из выражения (1.3) получим:
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
и
Решение. Прямая (1.5) имеет направляющий вектор q1=(m1, p1)=(3, 4), а прямая (1.6) − q2=(m2, p2)=(− 3, 1). Для определения угла между прямыми (1.5) и (1.6) подставим значения m1, p1, m2, p2 в (1.4):
Упростим и решим:
Найдем угол φ
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
Ответ.
Угол между прямыми равен:
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
Сделаем преобразования с выражением (1.7):
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
Пример 2. Определить, параллельны ли прямые
и
Решение. Прямая (1.10) имеет направляющий вектор q1=(m1, p1)=(3, 3), а прямая (1.11) − q2=(m2, p2)=(−2, −2). Тогда
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
и
Решение. Прямая (1.14) имеет направляющий вектор q1=(m1, p1)=(3, 1), а прямая (1.15) − q2=(m2, p2)=(−2, 6). Тогда
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
и
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
Из определения скалярного произведения двух векторов, имеем:
где |n1| и |n2| модули нормальных векторов n1 и n2 соответственно, φ -угол между векторами n1 и n2.
Из уравнения (19) получим
Пример 4. Найти угол между прямыми
и
Решение. Прямая (1.21) имеет нормальный вектор n1=(A1, B1)=(5, −2), а прямая (1.22) − n2=(A2, B2)=(1, 3). Задача определения угла между прямыми L1 и L2 сводится к определению угла между векторами n1 и n2. Из определения скалярного произведения векторов имеем: (n1,n2)=|n1||n2|cosφ. Тогда
Подставляя значения A1, B1, A2, B2 в (1.23), получим:
Упростим и решим:
Найдем угол φ:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
и
Решение. Прямая (1.26) имеет нормальный вектор n1=(A1, B1)=(4, 2), а прямая (1.27) − n2=(A2, B2)=(2, 1). Тогда подставляя значения A1, B1, A2, B2 в (1.24), получим
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
и
Решение. Прямая (1.29) имеет нормальный вектор n1=(A1, B1)=(4, −1), а прямая (1.30) − n2=(A2, B2)=(2, 8). Тогда подставляя значения A1, B1, A2, B2 в (28), получим
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
и
где q1=(m1, p1, l1) направляющий вектор прямой L1, а q2=(m2, p2, l2) направляющий вектор прямой L2.
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
Из определения скалярного произведения:
где |q1| и |q2| модули направляющих векторов q1 и q2 соответственно, φ -угол между векторами q1 и q2.
Из выражения (2.3) получим:
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
и
Решение. Прямая (2.5) имеет направляющий вектор q1=(m1, p1, l1)=(1, 1, 3), а прямая (2.6) − q2=(m2, p2, l2)=(− 3, 1, 2). Для определения угла между прямыми (2.5) и (2.6) подставим значения m1, p1, l1, m2, p2, l2 в (2.4):
Упростим и решим:
Найдем угол φ
Ответ.
Угол между прямыми равен:
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
и
Решение. Прямая (2.9) имеет направляющий вектор q1=(m1, p1, l1)=(3, 2, 4), а прямая (2.10) − q2=(m2, p2, l2)=(6, 4, 8). Тогда
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
и
Решение. Прямая (2.9) имеет направляющий вектор q1=(m1, p1, l1)=(1, 2, 0), а прямая (2.10) − q2=(m2, p2, l2)=(2, 4, 0). Подставляя значения m1, p1, l1, m2, p2, l2 в (2.8), получим
Выражение (2.13) нужно понимать так:
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
Пример 3. Определить, перпендикулярны ли прямые
и
Решение. Прямая (2.16) имеет направляющий вектор q1=(m1, p1, l1)=(3, 2, 1), а прямая (2.17) − q2=(m2, p2, l2)=(4, −6, 0). Тогда
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Угол между двумя прямыми
Угол φ между
двумя прямыми, заданными общими
уравнениями A1x
+ B1y
+ C1 =
0 и A2x
+ B2y
+ C2 =
0, вычисляется по формуле:
Угол φ между
двумя прямыми, заданными каноническими
уравнениями (x-x1)/m1 =
(y-y1)/n1 и
(x-x2)/m2 =
(y-y2)/n2,
вычисляется по формуле:
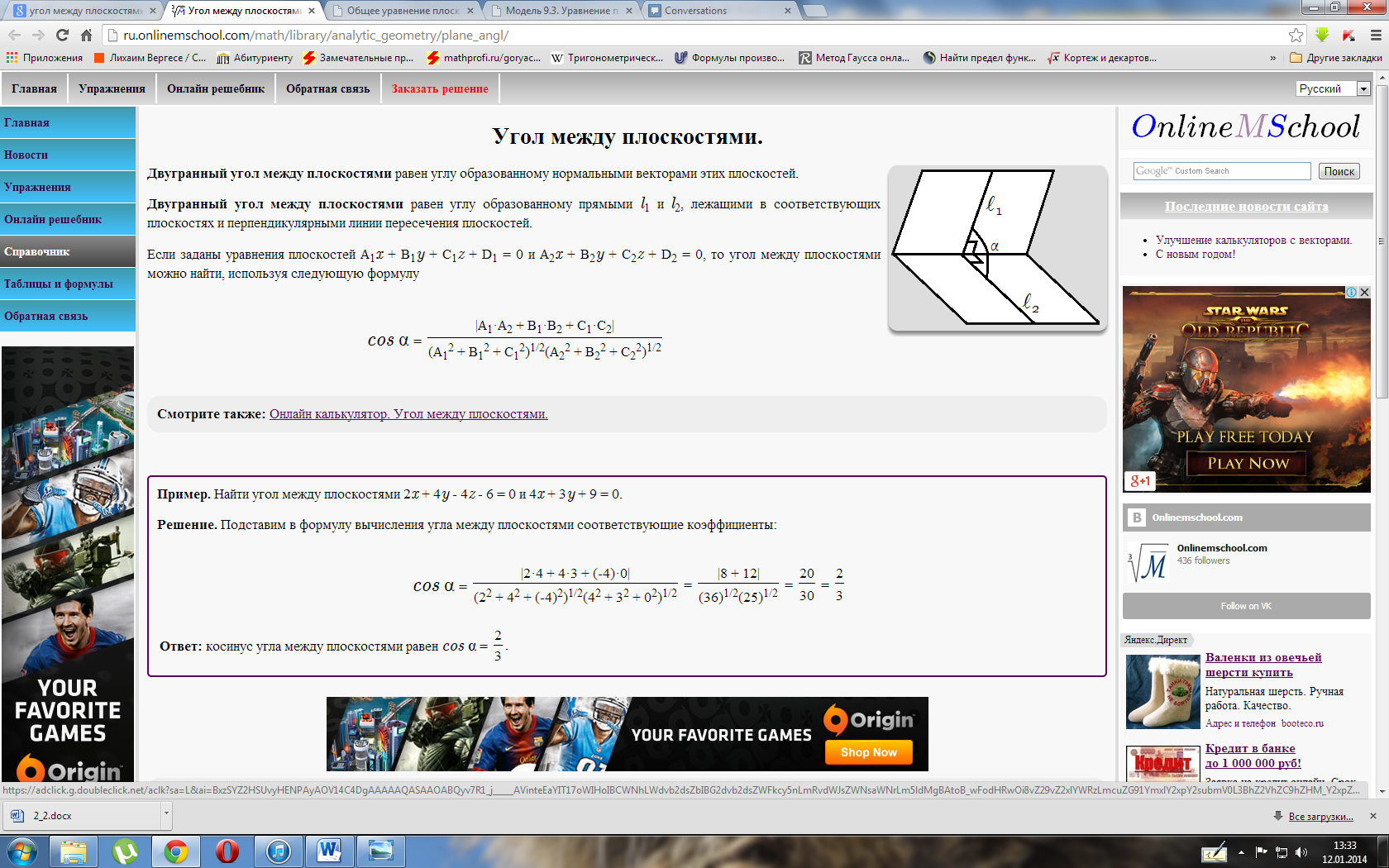
Расстояние от точки до прямой
3,2
Каждую
плоскость в пространстве можно представить
как линейное уравнение, называемое общим
уравнением плоскости
,
Частные
случаи.
o Если
в уравнении (8) ,
то плоскость проходит через начало
координат.
o При (
,
)
плоскость параллельна оси(оси
,
оси)
соответственно.
o При (
,
) плоскость
параллельна плоскости(плоскости
,
плоскости).
Решение:
используем (7)
,
.
Ответ:
общее уравнение плоскости .
-
Пример.
Плоскость
в прямоугольной системе координат Oxyz задана
общим уравнением плоскости .
Запишите координаты всех нормальных
векторов этой плоскости.
Решение.
Нам
известно, что коэффициенты при
переменных x, y и z в общем
уравнении плоскости являются
соответствующими координатами нормального
вектора этой плоскости. Следовательно,
нормальный вектор заданной
плоскостиимеет
координаты.
Множество всех нормальных векторов
можно задать как.
Ответ:
-
Пример.
Напишите
уравнение плоскости, если в прямоугольной
системе координат Oxyz в пространстве
она проходит через точку ,
а—
нормальный вектор этой плоскости.
Решение.
Приведем
два решения этой задачи.
Из
условия имеем .
Подставляем эти данные в общее уравнение
плоскости, проходящей через точку:
-
Пример.
Напишите
общее уравнение плоскости параллельной
координатной плоскости Oyz и
проходящей через точку .
Решение.
Плоскость,
которая параллельна координатной
плоскости Oyz, может быть задана общим
неполным уравнением плоскости вида .
Так как точкапринадлежит
плоскости по условию, то координаты
этой точки должны удовлетворять уравнению
плоскости,
то есть, должно быть справедливо
равенство.
Отсюда находим.
Таким образом, искомое уравнение имеет
вид.
Решение. Векторное
произведение по определению
10.26 ортогонально
векторам p и q.
Следовательно, оно ортогонально искомой
плоскости и вектор можно
взять в качестве ее нормального вектора.
Найдем координаты вектора n:
то
есть .
Используя формулу (11.1),
получим
Раскрыв
в этом уравнении скобки, приходим к
окончательному ответу.
Ответ: .
-
Найти
единичный нормальный вектор плоскости.
Перепишем
вектор нормали в виде и
найдём его длину:
Согласно
вышесказанному:
Ответ:
-
Построить
плоскость, проходящую через
точкупараллельно
плоскости.
У
параллельных плоскостей один и тот же
вектор нормали. 1) Из уравнения найдём
вектор нормали плоскости:.
2)
Уравнение плоскости составим
по точкеи
вектору нормали:
Ответ:
Векторное
уравнение плоскости в пространстве
Параметрическое
уравнение плоскости в пространстве
Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору
Пусть
в трехмерном пространстве задана
прямоугольная декартова система
координат. Сформулируем следующую
задачу:
Составить
уравнение плоскости, проходящей через
данную точку
M(x0,
y0,
z0) перпендикулярно
данному вектору
n =
{A, B, C}
.
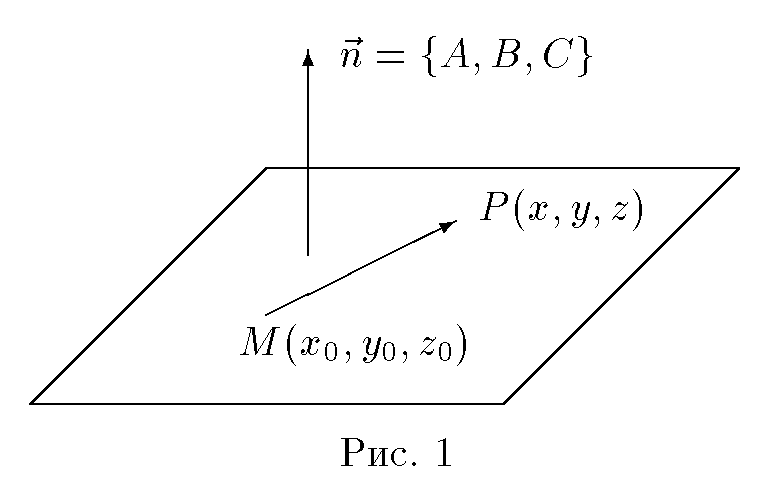
Решение. Пусть P(x, y, z)
— произвольная точка пространства.
Точка P принадлежит
плоскости тогда и только тогда, когда
вектор
MP =
{x − x0, y − y0, z − z0}
ортогонален вектору n =
{A, B, C}
(рис.1).
Написав
условие ортогональности этих векторов
(n, MP)
= 0 в координатной форме, получим:
|
A(x − x0) |
Уравнение
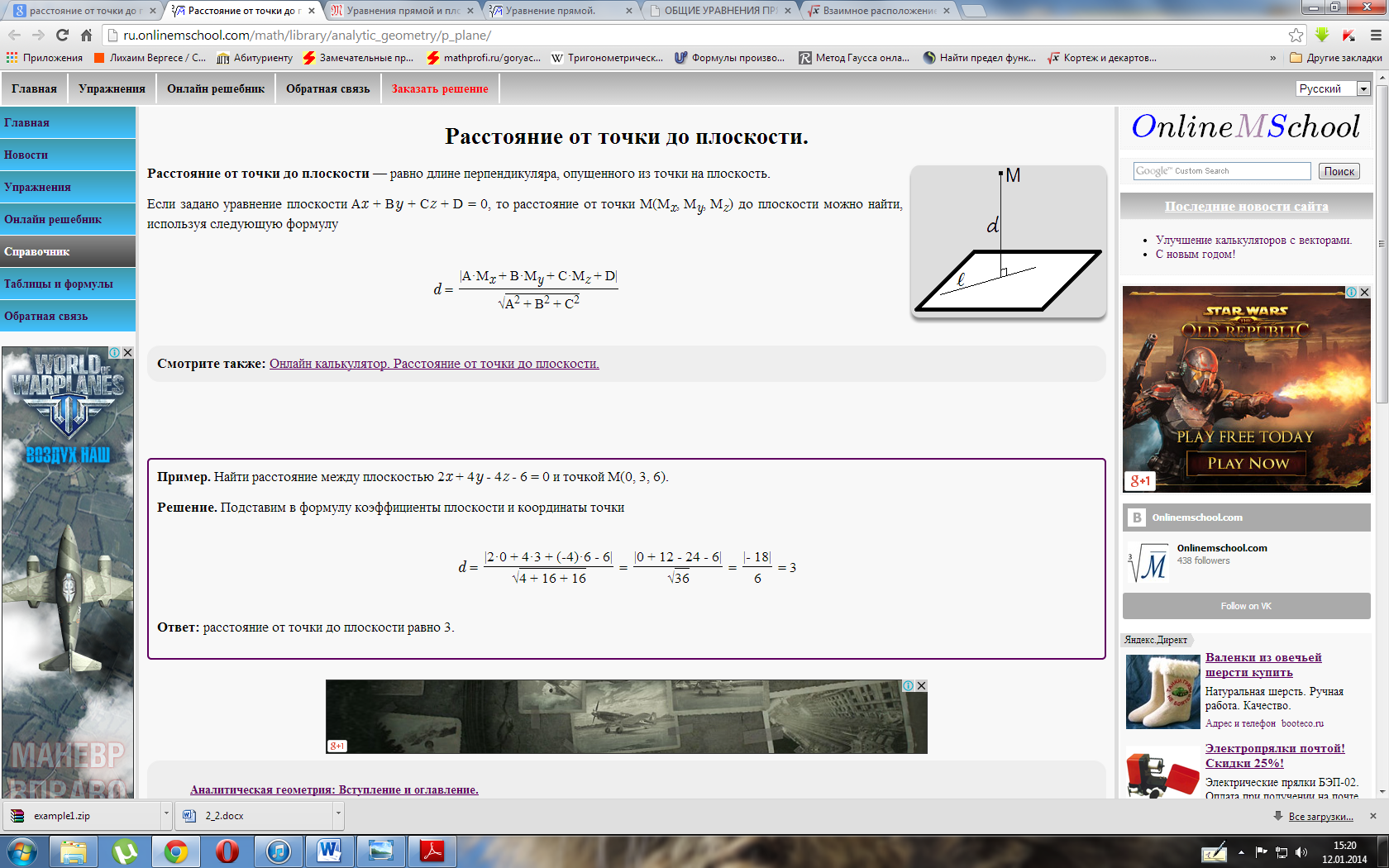
плоскости по трем точкам
В
векторном виде
В
координатах
Взаимное
расположение плоскостей в пространстве
Пусть
и
– общие уравнения двух
плоскостей. Тогда:
1)
если ,
то плоскости совпадают;
2)
если ,
то плоскости параллельны;
3)
если или
,
то плоскости пересекаются и системауравнений
(6)
является
уравнениями прямой пересечения данных
плоскостей.
3.3
Решение:
Ответ: |
Берём |
Составить
параметрические уравнения следующих
прямых:
Решение:
Прямые заданы каноническими уравнениями
и на первом этапе следует найти
какую-нибудь точку, принадлежащую
прямой, и её направляющий вектор.
а)
Из уравнений снимаем
точку и направляющий вектор: .
Точку можно выбрать и другую (как это
сделать – рассказано выше), но лучше
взять самую очевидную. Кстати, во
избежание ошибок, всегда подставляйте
её координаты в уравнения.
Составим
параметрические уравнения данной
прямой:
Удобство
параметрических уравнений состоит в
том, что с их помощью очень легко находить
другие точки прямой. Например, найдём
точку ,
координаты которой, скажем, соответствуют
значению параметра :
Таким
образом:
б)
Рассмотрим канонические уравнения .
Выбор точки здесь несложен, но
коварен: (будьте
внимательны, не перепутайте координаты!!!).
Как вытащить направляющий вектор? Можно
порассуждать, чему параллельна данная
прямая, а можно использовать простой
формальный приём: в пропорции находятся
«игрек» и «зет», поэтому запишем
направляющий вектор ,
а на оставшееся место поставим ноль: .
Составим
параметрические уравнения прямой:
в)
Перепишем уравнения в
виде ,
то есть «зет» может быть любым. А если
любым, то пусть, например, .
Таким образом, точка принадлежит
данной прямой. Для нахождения направляющего
вектора используем следующий формальный
приём: в исходных уравнениях находятся
«икс» и «игрек», и в направляющем векторе
на данных местах записываем нули: .
На оставшееся место ставим единицу: .
Вместо единицы подойдёт любое число,
кроме нуля.
Запишем
параметрические уравнения прямой:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Угол между прямыми онлайн
С помощью этого онлайн калькулятора можно найти угол между прямыми. Дается подробное решение с пояснениями. Для вычисления угла между прямыми, задайте размерность (2-если рассматривается прямая на плоскости, 3- если рассматривается прямая в пространстве), выберите вид уравнения (канонический, параметрический, общий (для двухмерного пространства)), введите данные в ячейки и нажмите на кнопку «Решить». Теоретическую часть и численные примеры смотрите ниже.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
1. Угол между прямыми на плоскости
Прямые заданы каноническими уравнениями
1.1. Определение угла между прямыми
Пусть в двухмерном пространстве прямые L1 и L2 заданы каноническими уравнениями
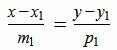 , , |
(1.1) |
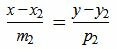 , , |
(1.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 (рис.1).
 , , |
(1.3) |
Из выражения (1.3) получим:
Таким образом, из формулы (1.4) можно найти угол между прямыми L1 и L2. Как видно из Рис.1 пересекающиеся прямые образуют смежные углы φ и φ1. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (1.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
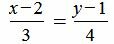 . . |
(1.5) |
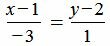 . . |
(1.6) |
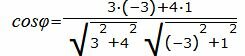
Упростим и решим:
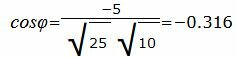
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
Угол между прямыми равен:
1.2. Условие параллельности прямых
Пусть φ=0. Тогда cosφ=1. При этом выражение (1.4) примет следующий вид:
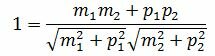 . . |
(1.7) |
Сделаем преобразования с выражением (1.7):
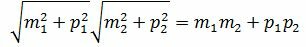
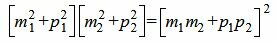
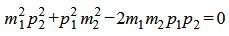
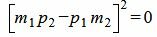
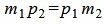 . . |
(1.8) |
Таким образом условие параллельности прямых L1 и L2 имеет вид (1.8). Если m2≠0 и p2≠0, то (1.8) можно записать так:
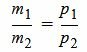 . . |
(1.9) |
Пример 2. Определить, параллельны ли прямые
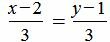 . . |
(1.10) |
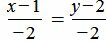 . . |
(1.11) |
Удовлетворяется равенство (1.9), следовательно прямые (1.10) и (1.11) параллельны.
Ответ. Прямые (1.10) и (1.11) параллельны.
1.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (1.4) примет следующий вид:
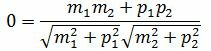 . . |
(1.12) |
Правая часть выражения (1.12) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
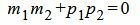 . . |
(1.13) |
Пример 3. Определить, перпендикулярны ли прямые
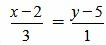 |
(1.14) |
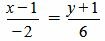 . . |
(1.15) |
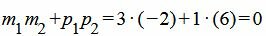 . . |
(16) |
Удовлетворяется условие (1.13), следовательно прямые (1.14) и (1.15) перпендикулярны.
Ответ. Прямые (1.14) и (1.15) перпендикулярны.
Прямые заданы общими уравнениями
1.4. Определение угла между прямыми
Пусть две прямые L1 и L2 заданы общими уравнениями
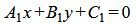 |
(1.17) |
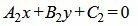 . . |
(1.18) |
Так как нормальным вектором прямой L1 является n1=(A1, B1), а нормальным вектором прямой L2 является n2=(A2, B2), то задача об определении угла между прямыми L1 и L2 сводится к определению угла φ между векторами n1 и n2 (Рис.2).
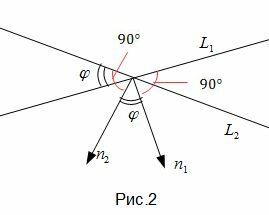
Из определения скалярного произведения двух векторов, имеем:
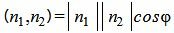 . . |
(1.19) |
Из уравнения (19) получим
Пример 4. Найти угол между прямыми
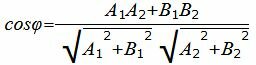 |
(23) |
Упростим и решим:
Данный угол больше 90°. Найдем минимальный угол между прямыми. Для этого вычтем этот угол из 180:
1.5. Условие параллельности прямых
Так как угол между паралленьными прямыми равен нулю, то φ=0, cos(φ)=1. Тогда сделав преобразования, представленные выше для канонических уравнений прямых получим условие параллельности:
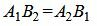 . . |
(1.24) |
С другой стороны условие параллельности прямых L1 и L2 эквивалентно условию коллинеарности векторов n1 и n2 и можно представить так:
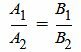 . . |
(1.25) |
Как видим уравнения (1.24) и (1.25) эквивалентны при A2≠0 и B2≠0. Если в координатах нормальных векторов существует нулевой коэффициент, то нужно использовать уравнение (1.24).
Пример 5. Определить, параллельны ли прямые
Удовлетворяется равенство (1.24), следовательно прямые (1.26) и (1.27) параллельны.
Ответ. Прямые (1.26) и (1.27) параллельны.
1.6. Условие перпендикулярности прямых
Условие перпендикулярности прямых L1 и L2 можно извлекать из формулы (1.20), подставляя cos(φ)=0. Тогда скалярное произведение (n1,n2)=0. Откуда
Таким образом условие перпендикулярности прямых определяется равенством (1.28).
Пример 6. Определить, перпендикулярны ли прямые
Удовлетворяется равенство (1.28), следовательно прямые (1.29) и (1.30) перпендикулярны.
Ответ. Прямые (1.29) и (1.30) перпендикулярны.
2. Угол между прямыми в пространстве
2.1. Определение угла между прямыми
Пусть в пространстве прямые L1 и L2 заданы каноническими уравнениями
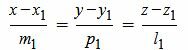 , , |
(2.1) |
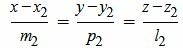 , , |
(2.2) |
Задача об определении угла между прямыми L1 и L2 сводится к задаче об определении угла между направляющими векторами q1 и q2 .
 , , |
(2.3) |
Из выражения (2.3) получим:
Таким образом, из формулы (2.4) можно найти угол между прямыми L1 и L2. Если найденный угол больше 90°, то можно найти минимальный угол между прямыми L1 и L2: φ1=180-φ.
Из формулы (2.4) можно вывести условия параллельности и перпендикулярности двух прямых.
Пример 1. Определить угол между прямыми
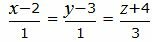 . . |
(2.5) |
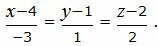 |
(2.6) |
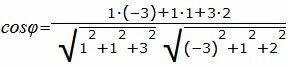
Упростим и решим:
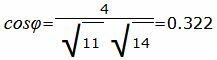
Угол между прямыми равен:
2.2. Условие параллельности прямых
Условие параллельности прямых эквивалентно условию коллинеарности направляющих векторов q1 и q2, т.е. соответствующие координаты этих векторов пропорциональны. Пусть
| m1=αm2, p1=αp2, l1=αl2 | (2.7) |
где α − некоторое число. Тогда соответствующие координаты векторов q1 и q2 пропорциональны, и, следовательно прямые L1 и L2 параллельны.
Условие параллельности прямых можно представить и так:
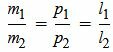 |
(2.8) |
Отметим, что любую пропорцию 
Пример 2. Определить, параллельны ли прямые
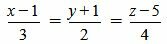 . . |
(2.9) |
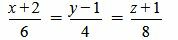 . . |
(2.10) |
Удовлетворяется равенство (2.8) (или (2.7)), следовательно прямые (2.9) и (2.10) параллельны.
Ответ. Прямые (2,9) и (2,10) параллельны.
Пример 3. Определить, параллельны ли прямые
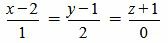 . . |
(2.11) |
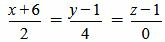 . . |
(2.12) |
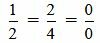 . . |
(2.13) |
Выражение (2.13) нужно понимать так:
Как мы видим из (2.14) условия (2.13) выполняются. Следовательно прямые (2.11) и (2.12) параллельны.
Ответ. Прямые (2.11) и (2.12) параллельны.
2.3. Условие перпендикулярности прямых
Пусть φ=90°. Тогда cosφ=0. При этом выражение (2.4) примет следующий вид:
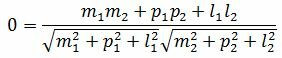 . . |
(2.15) |
Правая часть выражения (2.15) равно нулю тогда и только тогда, когда числитель равен нулю. Следовательно, для того, чтобы прямые L1 и L2 были перпендикулярны , должно выполняться условие
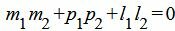 . . |
(2.16) |
Пример 3. Определить, перпендикулярны ли прямые
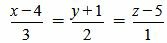 |
(2.17) |
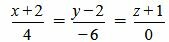 . . |
(2.18) |
Удовлетворяется условие (2.16), следовательно прямые (2.17) и (2.18) перпендикулярны.
Ответ. Прямые (2.17) и (2.18) перпендикулярны.
Угол между прямыми
Определение угла между прямыми
Угол между прямыми на плоскости
Угол между прямыми заданными уравнениями с угловым коэффициентом
то угол между ними можно найти, используя формулу:
Если знаменатель равен нулю (1 + k 1· k 2 = 0), то прямые перпендикулярны.
Соответственно легко найти угол между прямыми
tg γ = tg ( α — β ) = tg α — tg β 1 + tg α ·tg β = k 1 — k 2 1 + k 1· k 2
Угол между прямыми через направляющие векторы этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано параметрически
x = l t + a y = m t + b
то вектор направляющей имеет вид
Если уравнение прямой задано как
то для вычисления направляющего вектора, можно взять две точки на прямой.
Например, если C ≠ 0, A ≠ 0, C ≠ 0 , при x = 0 => y = — C B значит точка на прямой имеет координаты K(0, — C B ), при y = 0 => x = — C A значит точка на прямой имеет координаты M(- C A , 0). Вектор направляющей KM = .
Если дано каноническое уравнение прямой
то вектор направляющей имеет вид
Если задано уравнение прямой с угловым коэффициентом
то для вычисления направляющего вектора, можно взять две точки на прямой, например, при x = 0 => y = b значит точка на прямой имеет координаты K(0, b ), при x = 1 => y = k + b значит точка на прямой имеет координаты M(1, k + b ). Вектор направляющей KM =
Угол между прямыми через векторы нормалей этих прямых
cos φ = | a · b | | a | · | b |
Если уравнение прямой задано как
то вектор нормали имеет вид
Если задано уравнение прямой с угловым коэффициентом
то вектор нормали имеет вид
Угол между прямыми через направляющий вектор и вектор нормали этих прямых
sin φ = | a · b | | a | · | b |
Примеры задач на вычисления угла между прямыми на плоскости
Решение: Воспользуемся формулой для вычисления угла между прямыми заданными уравнениями с угловым коэффициентом:
tg γ = k 1 — k 2 1 + k 1· k 2 = 2 — (-3) 1 + 2·(-3) = 5 -5 = 1
Решение: Воспользуемся формулой для вычисления угла между прямыми у которых известны направляющие векторы.
Для первой прямой направляющий вектор <1; 2>, для второй прямой направляющий вектор
cos φ = |1 · 2 + 2 · 1| 1 2 + 2 2 · 2 2 + 1 2 = 4 5 · 5 = 0.8
Решение: Для решения этой задачи можно найти направляющие векторы и вычислить угол через направляющие векторы или преобразовать уравнения в уравнения с угловым коэффициентом и вычислить угол через угловые коэффициенты.
Преобразуем имеющиеся уравнения в уравнения с угловым коэффициентом.
2 x + 3 y = 0 => y = — 2 3 x ( k 1 = — 2 3 )
x — 2 3 = y 4 => y = 4 3 x — 8 3 ( k 2 = 4 3 )
tg γ = k 1 — k 2 1 + k 1· k 2 = — 2 3 — 4 3 1 + (- 2 3 )· 4 3 = — 6 3 1 — 8 9 = 18
Угол между прямыми в пространстве
cos φ = | a · b | | a | · | b |
Если дано каноническое уравнение прямой
то направляющий вектор имеет вид
Если уравнение прямой задано параметрически
x = l t + a y = m t + b z = n t + c
то направляющий вектор имеет вид
Решение: Так как прямые заданы параметрически, то <2; 1; -1>- направляющий вектор первой прямой, <1; -2; 0>направляющий вектор второй прямой.
cos φ = |2 · 1 + 1 · (-2) + (-1) · 0| 2 2 + 1 2 + (-1) 2 · 1 2 + (-2) 2 + 0 2 = 0 6 · 5 = 0
Решение: Для решения этой задачи найдем направляющие векторы этих прямых.
Уравнение первой прямой задано в канонической форме, поэтому направляющий вектор <3; 4; 5>.
Преобразуем второе уравнение к каноническому вид.
1 — 3 y = 1 + y -1/3 = y — 1/3 -1/3
3 z — 5 2 = z — 5/3 2/3
Получено уравнение второй прямой в канонической форме
x — 2 -2 = y — 1/3 -1/3 = z — 5/3 2/3
<-2; — 1 3 ; 2 3 >- направляющий вектор второй прямой.
cos φ = 3·(-2) + 4·(- 1 3 ) + 5· 2 3 3 2 + 4 2 + 5 2 · (-2) 2 + (- 1 3 ) 2 + ( 2 3 ) 2 = -6 — 4 3 + 10 3 9 + 16 + 25 · 4 + 1 9 + 4 9 = -4 50 · 41/9 = 12 5 82 = 6 82 205
Угол между двумя прямыми
Буду кратким. Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x1; y1; z1) и b = (x2; y2; z2), то сможете найти угол. Точнее, косинус угла по формуле:
Посмотрим, как эта формула работает на конкретных примерах:
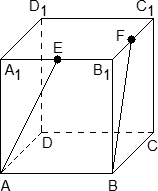
Задача. В кубе ABCDA1B1C1D1 отмечены точки E и F — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AE и BF.
Поскольку ребро куба не указано, положим AB = 1. Введем стандартную систему координат: начало в точке A, оси x, y, z направим вдоль AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1. Теперь найдем координаты направляющих векторов для наших прямых.
Найдем координаты вектора AE. Для этого нам потребуются точки A = (0; 0; 0) и E = (0,5; 0; 1). Поскольку точка E — середина отрезка A1B1, ее координаты равны среднему арифметическому координат концов. Заметим, что начало вектора AE совпадает с началом координат, поэтому AE = (0,5; 0; 1).
Теперь разберемся с вектором BF. Аналогично, разбираем точки B = (1; 0; 0) и F = (1; 0,5; 1), т.к. F — середина отрезка B1C1. Имеем:
BF = (1 − 1; 0,5 − 0; 1 − 0) = (0; 0,5; 1).
Итак, направляющие векторы готовы. Косинус угла между прямыми — это косинус угла между направляющими векторами, поэтому имеем:
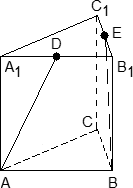
Задача. В правильной трехгранной призме ABCA1B1C1, все ребра которой равны 1, отмечены точки D и E — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AD и BE.
Введем стандартную систему координат: начало координат в точке A, ось x направим вдоль AB, z — вдоль AA1. Ось y направим так, чтобы плоскость OXY совпадала с плоскостью ABC. Единичный отрезок равен AB = 1. Найдем координаты направляющих векторов для искомых прямых.
Для начала найдем координаты вектора AD. Рассмотрим точки: A = (0; 0; 0) и D = (0,5; 0; 1), т.к. D — середина отрезка A1B1. Поскольку начало вектора AD совпадает с началом координат, получаем AD = (0,5; 0; 1).
Теперь найдем координаты вектора BE. Точка B = (1; 0; 0) считается легко. С точкой E — серединой отрезка C1B1 — чуть сложнее. Имеем:
Осталось найти косинус угла:
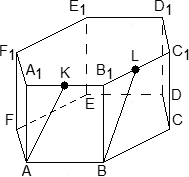
Задача. В правильной шестигранной призме ABCDEFA1B1C1D1E1F1, все ребра которой равны 1, отмечены точки K и L — середины ребер A1B1 и B1C1 соответственно. Найдите угол между прямыми AK и BL.
Введем стандартную для призмы систему координат: начало координат поместим в центр нижнего основания, ось x направим вдоль FC, ось y — через середины отрезков AB и DE, а ось z — вертикально вверх. Единичный отрезок снова равен AB = 1. Выпишем координаты интересующих нас точек:
Точки K и L — середины отрезков A1B1 и B1C1 соответственно, поэтому их координаты находятся через среднее арифметическое. Зная точки, найдем координаты направляющих векторов AK и BL:
Теперь найдем косинус угла:
Задача. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, отмечены точки E и F — середины сторон SB и SC соответственно. Найдите угол между прямыми AE и BF.
Введем стандартную систему координат: начало в точке A, оси x и y направим вдоль AB и AD соответственно, а ось z направим вертикально вверх. Единичный отрезок равен AB = 1.
Точки E и F — середины отрезков SB и SC соответственно, поэтому их координаты находятся как среднее арифметическое концов. Выпишем координаты интересующих нас точек:
A = (0; 0; 0); B = (1; 0; 0)
Зная точки, найдем координаты направляющих векторов AE и BF:
Координаты вектора AE совпадают с координатами точки E, поскольку точка A — начало координат. Осталось найти косинус угла:
http://ru.onlinemschool.com/math/library/analytic_geometry/lines_angle/
http://www.berdov.com/ege/solid_geometry/line/