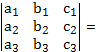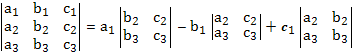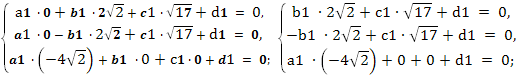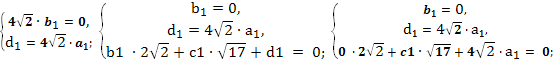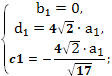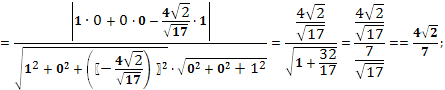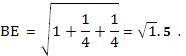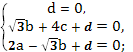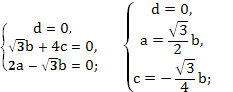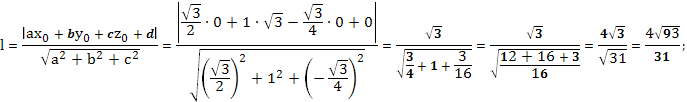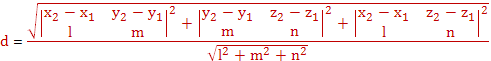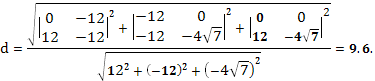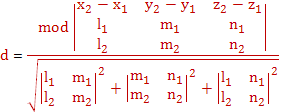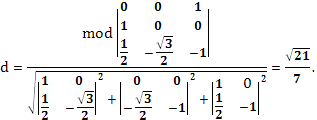11
Авг 2013
Категория: Справочные материалы
Углы в пространстве
2013-08-11
2014-03-03
Угол между пересекающимися прямыми
Углом между пересекающимися прямыми, называется наименьший из углов, образованных при пересечении этих прямых (если при пересечении образовались четыре равных угла, то прямые перпендикулярны).
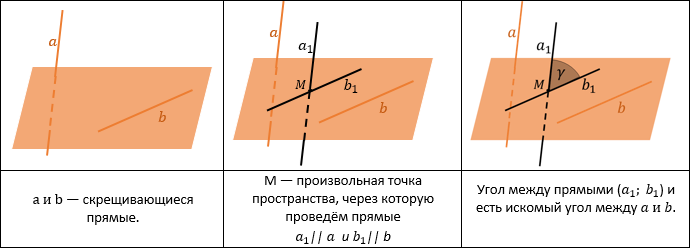
Угол между скрещивающимися прямыми
Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.
(Одну из прямых можно вполне и не переносить параллельно самой себе, а ограничиться только параллельным переносом одной из прямых до пересечения со второй).
Угол между прямой и плоскостью
Угол между прямой и плоскостью – угол между прямой и ее проекцией на плоскость
Угол между плоскостями
Угол между плоскостями равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.
Этот угол не зависит от выбора такой плоскости.
Угол между двумя параллельными плоскостями принимается равным нулю.
Автор: egeMax |
Нет комментариев
Углы
Классическим заданием с развернутым ответом на стереометрию является задача на нахождение угла. В стереометрии найти угол могут предложить между следующими комбинациями фигур:
Рассмотрим каждую комбинацию, чтобы понять, как искать разные виды углов и какие методы можно применять.
УГОЛ МЕЖДУ СКРЕЩИВАЮЩИМИСЯ ПРЯМЫМИ
Угол между скрещивающимися прямыми ― это угол между параллельными им прямыми, лежащими в одной плоскости.
Это значит, что никогда не пересекающиеся прямые в пространстве мы делаем «пересекающимися»: для этого нужно построить пересекающиеся прямые, параллельные данным. Угол между ними будет искомым.
Часто достаточно только к одной из скрещивающихся прямых построить параллельную прямую.
Например, если бы мы отметили точку M на прямой b и через точку M провели прямую $ a_1 parallel a $.
УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ
Угол между прямой и плоскостью — угол между прямой и ее проекцией на эту плоскость.
Для того, чтобы найти угол между прямой и плоскостью, нужно сначала получить проекцию этой прямой на плоскость, а потом найти угол.
|
|
|
|
|
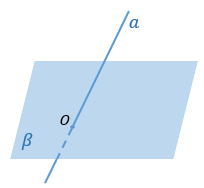
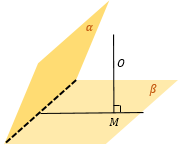
Прямая, пересекающая плоскость β в точке O |
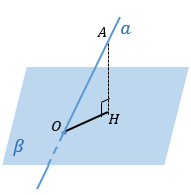
Из произвольной точки А на прямой опустим перпендикуляр AH на плоскость β. Тогда OH – проекция прямой на плоскость β. |
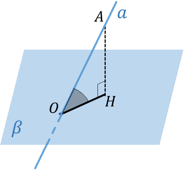
Угол между прямой и наклонной, то есть ∠ AOH и есть искомый угол между . |
УГОЛ МЕЖДУ ПЛОСКОСТЯМИ
Для начала вспомним пару определений:
Метод перпендикуляров к линии пересечения.Нахождения угла между плоскостями – одна из самых сложных задач на углы, поэтому тут мы можем воспользоваться несколькими методами.
Угол между плоскостями вычисляется как угол между прямыми, лежащими в этих плоскостях и перпендикулярными к линии их пересечения. Это основной способ нахождения угла между плоскостями.
|
|
|
|
|
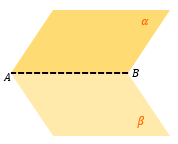
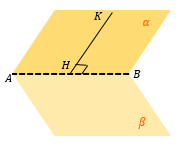
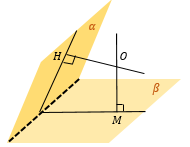
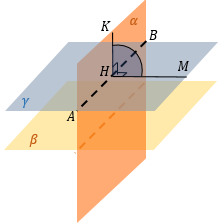
Находим линию пересечения плоскостей α и β – AB. |
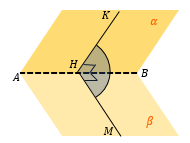
Из «удобной» точки К в плоскости α (это может быть вершина многогранника, середина ребра и т.д.) опускаем перпендикуляр KH на AB. |
В точку H опустим перпендикуляр из точки M в плоскости β. ∠ KHM – искомый угол между плоскостями α и β |
- Метод перпендикуляров к плоскостям.
Угол между плоскостями вычисляется как угол между перпендикулярами к данным плоскостям. Этот способ удобен, если перпендикуляр к плоскости построить удобнее, чем построить перпендикуляры к линии пересечения плоскостей (или перпендикуляр к плоскости уже есть по условию задачи).
|
|
|
|
|
Из произвольной точки O пространства опустим перпендикуляр OM на плоскость β. |
Из точки O опустим так же перпендикуляр OH на плоскость α. |
Любой из двух смежных углов между OM и OH может считать искомым, но так как угол между плоскостями измеряется от 0 до 90°, то берем острый. ∠ MOK – искомый угол между плоскостями α и β |
- Метод параллельных плоскостей.
Угол между плоскостями вычисляется как угол между плоскостями, параллельными данным плоскостям. Этот способ применим, когда угол между данными плоскостями по каким-то причинам искать неудобно, а удобнее найти угол между плоскостями, параллельными данным.
|
|
|
|
|
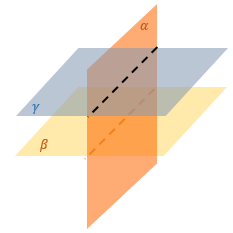
Угол между плоскостями α и β затруднительно искать (например, нет «удобных точек» или тяжело построить взаимные перпендикуляры). |
Построим плоскость γ, параллельную β (или в стереометрической фигуре она уже есть) |
По методу перпендикуляров к линии пересечения найдем угол между плоскостями α и γ. ∠ MНK – искомый угол между плоскостями α и β |
({color{red}{textbf{Факт 1. Про векторы}}})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), то вектор (overrightarrow{AB}) имеет координаты [overrightarrow{AB} = {x_2-x_1;y_2-y_1;z_2-z_1}]
(bullet) Если в пространстве заданы два вектора (vec{a}
={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}), то:
(qquad blacktriangleright) сумма этих векторов (vec{a}+vec{b}={x_1+x_2;y_1+y_2;z_1+z_2})
(qquad blacktriangleright) разность этих векторов (vec{a}-vec{b}={x_1-x_2;y_1-y_2;z_1-z_2})
(qquad blacktriangleright) произведение вектора на число (lambda
vec{a}={lambda x_1;lambda
y_1;lambda z_1})
(bullet) Если в пространстве заданы две точки (A(x_1;y_1;z_1)) и (B(x_2;y_2;z_2)), а точка (O) — середина отрезка (AB), то (O) имеет координаты [Oleft(dfrac{x_1+x_2}2;dfrac{y_1+y_2}2;dfrac{z_1+z_2}2right)]
(bullet) Длина вектора (vec{a}={x;y;z}) обозначается (|vec{a}|) и вычисляется по формуле [|vec{a}|=sqrt{x^2+y^2+z^2}]
(bullet) Заметим, что расстояние между двумя точками есть не что иное, как длина вектора с началом и концом в этих точках.
({color{red}{textbf{Факт 2. Про скалярное произведение}}})
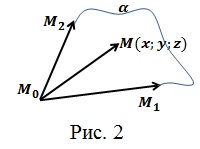
(bullet) Скалярным произведением двух векторов называется произведение длин этих векторов на косинус угла между ними: [{large{(vec{a},
vec{b})=|vec{a}|cdot|vec{b}|cdotcos angle (vec{a},
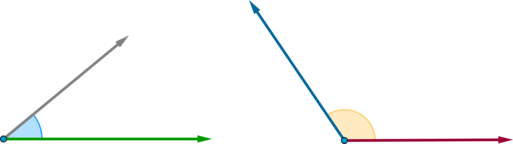
vec{b})}}] На рисунке показано, что такое угол между векторами:
(bullet) Справедливы следующие утверждения:
I. Скалярное произведение ненулевых векторов (их длины не равны нулю) равно нулю тогда и только тогда, когда они перпендикулярны: [(vec{a}, vec{b})=0 quadLeftrightarrowquad
vec{a}perp vec{b}]
II. Длина вектора равна квадратному корню из скалярного произведения вектора на себя: [|vec{a}|=sqrt{(vec{a},
vec{a})}]
III. Переместительный закон: [(vec{a}, vec{b})=(vec{b},
vec{a})]
IV. Распределительный закон: [(vec{a}+vec{b},
vec{c})=(vec{a}, vec{c})+(vec{b}, vec{c})]
V. Сочетательный закон ((lambda) – число): [lambda(vec{a}, vec{b})=(lambda
vec{a}, vec{b})]
(bullet) Скалярное произведение двух векторов (vec{a}
={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) можно вычислить с помощью координат этих векторов: [{large{(vec{a},
vec{b})=x_1x_2+y_1y_2+z_1z_2}}]
(bullet) Косинус угла между векторами (vec{a} ={x_1;y_1;z_1}) и (vec{b}= {x_2;y_2;z_2}) вычисляется по формуле: [{large{cosangle(vec{a}, vec{b})=dfrac{x_1x_2+y_1y_2+z_1z_2}
{sqrt{x^2_1+y^2_1+z^2_1}cdot
sqrt{x^2_2+y^2_2+z^2_2}}}}]
({color{red}{textbf{Факт 3. Про уравнение плоскости}}})
(bullet) Если (vec{n}={a;b;c}) – нормаль к плоскости, то уравнение плоскости имеет вид [ax+by+cz+d=0] Для того, чтобы найти (d), нужно подставить в уравнение плоскости вместо (x, y, z) координаты любой точки, лежащей в этой плоскости.
Пример: если (vec{n}={1;2;3}) – нормаль к плоскости, (O(4;5;6)) – точка из плоскости, то справедливо: (1cdot 4+2cdot 5+3cdot
6+d=0), откуда (d=-32), следовательно, уравнение плоскости имеет вид (x+2y+3z-32=0).
(bullet) Уравнение плоскости можно составить, используя три точки из плоскости, не лежащие на одной прямой.
Пусть (A(1;0;0),
B(0;3;4), C(2;0;5)) – точки из плоскости. Тогда уравнение плоскости можно найти, решив систему: [begin{cases}
1cdot a+0cdot b+0cdot c+d=0\
0cdot a+3cdot b+4cdot c+d=0\
2cdot a+0cdot b+5cdot c+d=0end{cases} quadRightarrowquad
begin{cases}
d=-a\
3b+4c-a=0\
a+5c=0end{cases}quadRightarrowquad begin{cases} d=-a\
a=-5c\
b=-3cend{cases}quadRightarrowquadbegin{cases}a=-5c\
b=-3c\
d=5cend{cases}] Следовательно, уравнение плоскости имеет вид: [-5ccdot x-3ccdot y+ccdot z+5c=0] Можно разделить обе части на (c), так как (cne 0) (иначе (a=b=c=d=0)), следовательно, уравнение плоскости имеет вид [-5x-3y+z+5=0]
({color{red}{textbf{Факт 4. Про углы между прямыми, плоскостями}}})
(bullet) Если векторы (vec{a} ={x_1;y_1;z_1}) и (vec{b}=
{x_2;y_2;z_2}) являются направляющими прямых (p) и (q), то косинус угла между этими прямыми равен: [cos phi=dfrac{|x_1x_2+y_1y_2+z_1z_2|}
{sqrt{x^2_1+y^2_1+z^2_1}cdot sqrt{x^2_2+y^2_2+z^2_2}}]
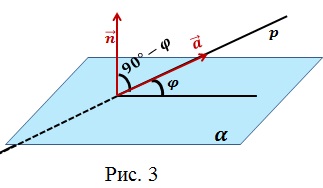
(bullet) Если (vec{a}) — направляющий вектор прямой (p), а (vec{n}) — нормаль к плоскости (phi) (перпендикуляр к плоскости), то синус угла между прямой (p) и плоскостью (phi) равен модулю косинуса угла между векторами (vec{a}) и (vec{n}): [sin
angle(p, phi)=|cos angle(vec{a}, vec{n})|]
(bullet) Если две плоскости заданы уравнениями (a_1x+b_1y+c_1z+d_1=0) и (a_2x+b_2y+c_2z+d_2=0), то косинус угла между плоскостями ищется по формуле: [{large{cos phi=left| dfrac{a_1a_2+b_1b_2+c_1c_2}
{sqrt{a^2_1+b^2_1+c^2_1}cdot
sqrt{a^2_2+b^2_2+c^2_2}}right|}}]
({color{red}{textbf{Факт 5. Про расстояния от точки до плоскости,
между скрещивающимися прямыми}}})
(bullet) Если (M(x_0;y_0;z_0)) — некоторая точка вне плоскости (phi), (ax+by+cz+d=0) — уравнение плоскости (phi), то расстояние от точки (M) до плоскости (phi) ищется по формуле: [rho(M, phi)=dfrac{|ax_0+by_0+cz_0+d|}{sqrt{a^2+b^2+c^2}}]
(bullet) Для того, чтобы найти расстояние между скрещивающимися прямыми, нужно
— построить плоскость, проходящую через одну из них и параллельную другой;
— найти уравнение этой плоскости;
— найти расстояние от любой точки первой прямой до этой плоскости.
Как вы знаете в задании С2 чаще всего требуется
найти:
1) угол между двумя скрещивающимися прямыми,
между прямой и плоскостью, между двумя
плоскостями;
2) расстояние между двумя скрещивающимися
прямыми, расстояние от точки до прямой, от точки
до плоскости.
Рассмотрим различные типы задач, решаемых
координатно-векторным методом.
Векторно-координатный метод — весьма
эффективный и универсальный способ нахождения
любых углов или расстояний между
стереометрическими объектами в пространстве.
1. Задача на нахождение угла между прямыми
Определение 1. Углом между скрещивающимися
прямыми в пространстве называется угол двумя
прямыми, параллельными данным, лежащими в одной
плоскости.
Градусная мера угла располагается в диапазоне
от 0° до 90°. Данный угол между двумя прямыми равен
углу между их направляющими векторами.
Определение 2. Направляющий вектор прямой —
это любой ненулевой вектор, лежащий на данной
прямой или на параллельной ей прямой.
Таким образом, если нам удастся найти
координаты направляющих векторов
и
, то сможем найти
угол.
Косинус угла
между ненулевыми векторами и
вычисляется по формуле:
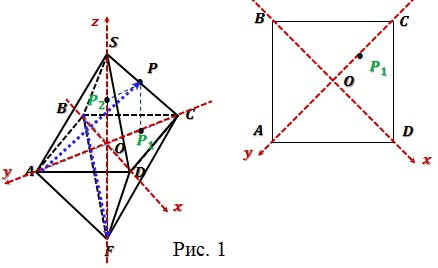
Задача 1 (Вариант 19). В правильном октаэдре SABCDF
(S и F – несмежные вершины) точка P –
середина ребра SC. Найдите косинус угла между
прямыми BF и AP.
Решение: Введем прямоугольную систему
координат, как показано на рисунке 1.
Пусть все ребра октаэдра равны 1. Найдем
координаты точек:
Пусть – угол между
и
– искомый угол между
прямыми BF и AP.
2. Задача на нахождение угла между прямой и
плоскостью
Определение 3. Углом между (пересекающимися)
прямой и плоскостью называется угол между прямой
и ее (ортогональной) проекцией на эту плоскость.
Определение 4. Определитель второго порядка
Определение 5. Определитель третьего порядка
Уравнение плоскости, проходящей через три
точки. не
лежащие на одной прямой.
.
Определение 6. Нормальный вектор плоскости —
это любой ненулевой вектор, лежащий на прямой
перпендикулярной к данной плоскости.
Пусть плоскость имеет нормальный вектор
А прямая
имеет
направляющий вектор .
Тогда синус угла между прямой и плоскостью
вычисляется по формуле:
Задача 2 (Вариант 14). В прямоугольном
параллелепипеде
Найдите угол между прямой
и плоскостью
.
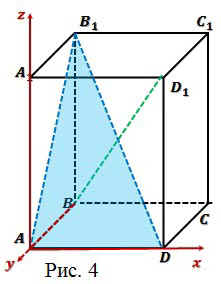
Решение: Введем прямоугольную систему
координат, как показано на рисунке 4.
Найдем координаты точек:
Определим координаты вектора .
Найдем координаты вектора , перпендикулярного
плоскости . Для этого составим уравнение
плоскости .
.
Пусть
– искомый угол между прямой и плоскостью
.
3. Задача на нахождение угла между плоскостями
Определение 7. Углом между (пересекающимися)
плоскостями называется угол между прямыми
пересечения этих плоскостей с плоскостью,
перпендикулярной прямой их пересечения.
Задачу о нахождении угла между плоскостями и
, заданными соответственно
уравнениями и
, можно свести к задаче о нахождении
угла
между их векторами нормали и
, а далее использовать
формулу
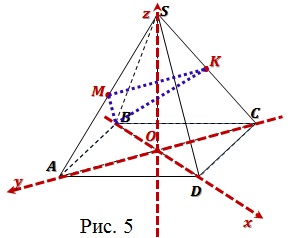
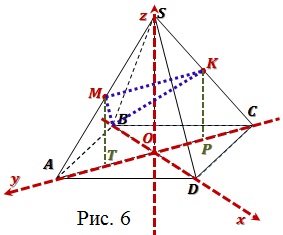
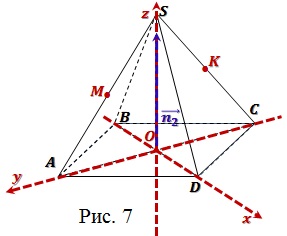
Задача 3. В правильной четырёхугольной
пирамиде SABCD точка S — вершина. Точка M
— середина ребра SA, точка K— середина
ребра SC. Найдите угол между плоскостями BMK
и ABC, если AB = 8, SC =10.
Решение: Введем прямоугольную систему
координат, как показано на рисунке 5.
;
.
4. Задача нахождение расстояние между двумя
точками.
Координаты середины отрезка
,
определяются по формулам:
Расстояние между точками и
вычисляется по формуле
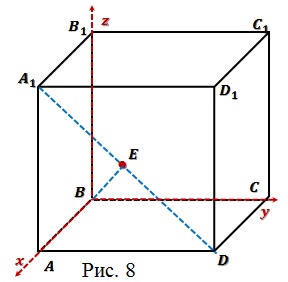
Задача 4. В кубе ABCDA1B1C1D1
с ребром 1 найти расстояние от точки B до
середины отрезка A1D.
Решение: Поместим наш куб в прямоугольную
систему координат как показано на рисунке 8.
Определим координаты точек:
Воспользуемся формулой расстояния между двумя
точками.
Пусть точка E – середина , тогда координаты
Ответ:
5. Задача на нахождение расстояние от точки до
плоскости
Чтобы найти расстояние от точки до плоскости,
необходимо опустить перпендикуляр из данной
точки на эту плоскость.
Расстояние от точки до плоскости, не содержащей
эту точку, есть длина отрезка перпендикуляра,
опущенного из этой точки на плоскость.
Пусть данная
точка,
уравнение
данной плоскости
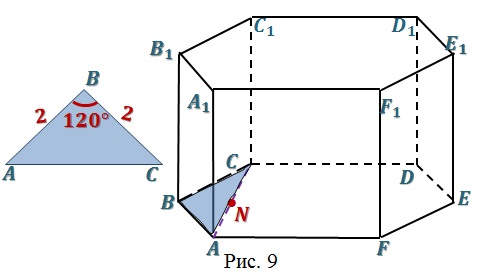
Задача 5 (Вариант 10). В правильной
шестиугольной призме стороны основания равны
, а боковые
ребра равны .
середина отрезка
. Найдите расстояние от
вершины
до плоскости
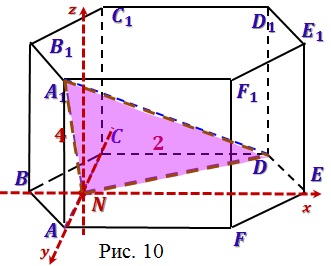
Решение: Введем прямоугольную систему
координат, как показано на рисунке 10.
Рассмотрим D АВС. По теореме косинусов:
Найдем координаты точек:
уравнение
данной плоскости
6. Задача на нахождение расстояния от точки до
прямой
Чтобы найти расстояние от точки до прямой,
необходимо опустить из точки перпендикуляр на
данную прямую.
Задача 6 (Вариант 18). Найдите расстояние от
вершины
основания правильной четырехугольной призмы до
диагонали , если сторона основания равна
, а боковое
ребро призмы .
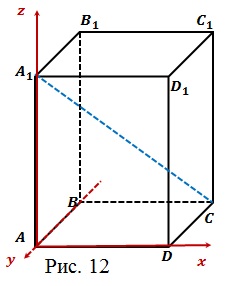
Решение: Введем прямоугольную систему
координат, как показано на рисунке 12.
Определим координаты точек:
Определим координаты вектора
7. Задача на нахождение расстояния между прямой
и плоскостью
- Расстояние от прямой до непараллельной ей
плоскости равно нулю. - Расстояние между прямой и параллельной ей
плоскостью равно длине отрезка их общего
перпендикуляра. - Расстояние от прямой до параллельной ей
плоскости равно расстоянию от любой точки
этой прямой до плоскости.
8. Задача на нахождение расстояния между двумя
прямыми
Чтобы найти расстояние между двумя
скрещивающимися прямыми, необходимо через одну
прямую провести плоскость, параллельную второй,
и найти расстояние от второй прямой до этой
плоскости.
Если скрещивающиеся прямые поместить в
параллельные плоскости, то расстояние между
этими прямыми будет равно расстоянию между
построенными плоскостями, а оно равно расстоянию
от любой точки одной прямой до плоскости,
содержащей вторую прямую.
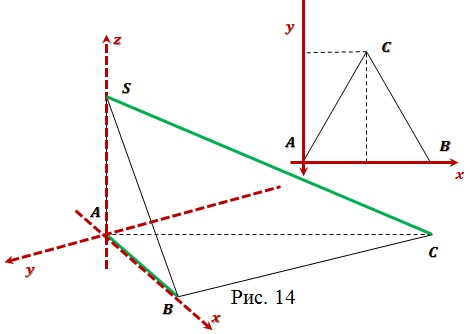
Задача 7 (Вариант 27). Основание пирамиды –
равносторонний треугольник со стороной 1.
Вершина проецируется
в точку ,
и .
Найдите расстояние между прямыми и
.
Решение: Введем прямоугольную систему
координат, как показано на рисунке 14.
Определим координаты точек:
Определим координаты векторов:
Знание различных подходов к решению
стереометрических задач позволяет выбрать
предпочтительный для любого учащегося способ, то
есть тот, которым ученик владеет уверенно,
помогает избежать ошибок, приводит к успешному
решению задачи и получению хорошего балла на
экзамене. Координатный метод имеет преимущество
перед другими способами.
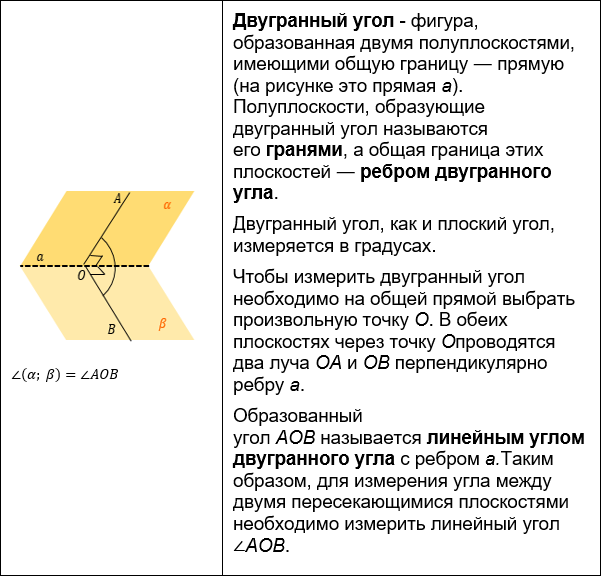
Угол между плоскостями. Перпендикулярность плоскостей
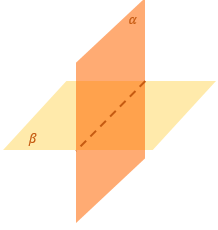
Пусть плоскости α и β пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.
Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.
Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны.
Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:
Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.
Читаем дальше: Угол и расстояние между скрещивающимися прямыми.
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Угол между плоскостями. Перпендикулярность плоскостей» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023