Как найти угол между векторами без координат - Исправление недочетов и поиск решений вместе с Examum.ru

Нахождение угла между векторами с помощью скалярного произведения

Косинус угла между векторами a⃗=(a1;a2)vec{a}=(a_{1};a_{2}) и b⃗=(b1;b2)vec{b}=(b_{1};b_{2}) может быть вычислен по формуле

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=a1⋅b1+a2⋅b2a12+a22⋅b12+b22.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}= frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}}{sqrt{a_{1}^{2}+a_{2}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}}}.

Следовательно, угол между векторами a⃗=(a1;a2)vec{a}=(a_{1};a_{2}) и b⃗=(b1;b2)vec{b}=(b_{1};b_{2}) может быть вычислен по формуле

(a⃗,b⃗^)=arccos⁡(a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣)=arccos⁡(a1⋅b1+a2⋅b2a12+a22⋅b12+b22).left(widehat{vec{a},vec{b}}right)=arccosleft(frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}right)=arccosleft(frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}}{sqrt{a_{1}^{2}+a_{2}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}}}right).

Пример 1

Найти угол между векторами a⃗=(1;−1)vec{a}=(1; -1) и b⃗=(1;2).vec{b}=(1; 2).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=1⋅1+(−1)⋅212+(−1)2⋅12+22=1−22⋅5=−110.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{1cdot1+(-1)cdot2}{sqrt{1^{2}+(-1)^{2}}cdot sqrt{1^{2}+2^{2}}}=frac{1-2}{sqrt{2}cdotsqrt{5}}=frac{-1}{sqrt{10}}.

(a⃗,b⃗^)=arccos⁡(−110)=arccos⁡(−1010).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{-1}{sqrt{10}} right )=arccosleft ( frac{-sqrt{10}}{10} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(−1010).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{-sqrt{10}}{10} right).

Пример 2

Найти угол между векторами a⃗=(2;3)vec{a}=(2; 3) и b⃗=(3;1).vec{b}=(3; 1).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=2⋅3+3⋅122+32⋅32+12=6+313⋅10=9130=9130130.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{2cdot3+3cdot1}{sqrt{2^{2}+3^{2}}cdot sqrt{3^{2}+1^{2}}}=frac{6+3}{sqrt{13}cdotsqrt{10}}=frac{9}{sqrt{130}}=frac{9sqrt{130}}{130}.

(a⃗,b⃗^)=arccos⁡(9130130).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{9sqrt{130}}{130} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(9130130).left ( widehat{vec{a},vec{b}} right )=arccos left ( frac{9sqrt{130}}{130} right ).

Косинус угла между векторами a⃗=(a1;a2;a3)vec{a}=(a_{1};a_{2};a_{3}) и b⃗=(b1;b2;b3)vec{b}=(b_{1};b_{2};b_{3}) может быть вычислен по формуле

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=a1⋅b1+a2⋅b2+a3⋅b3a12+a22+a32⋅b12+b22+b32.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}= frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}+a_{3}cdot b_{3}}{sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}.

Следовательно, угол между векторами a⃗=(a1;a2;a3)vec{a}=(a_{1};a_{2};a_{3}) и b⃗=(b1;b2;b3)vec{b}=(b_{1};b_{2};b_{3}) может быть вычислен по формуле

(a⃗,b⃗^)=arccos⁡(a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣)=arccos⁡(a1⋅b1+a2⋅b2+a3⋅b3a12+a22+a32⋅b12+b22+b32).left(widehat{vec{a},vec{b}}right)=arccosleft(frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}right)=arccosleft(frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}+a_{3}cdot b_{3}}{sqrt{a_{1}^{2}+a_{2}^{2}+ a_{3}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}+ b_{3}^{2}}}right).

Пример 3

Найти угол между векторами a⃗=(1;2;3)иb⃗=(1;−2;3).vec{a}=(1; 2; 3) и vec{b}=(1; -2; 3).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=1⋅1+2⋅(−2)+3⋅312+22+32⋅12+(−2)2+32=1−4+914⋅14=614=37.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{1cdot1+2cdot(-2)+3cdot3}{sqrt{1^{2}+2^{2}+3^{2}}cdot sqrt{1^{2}+(-2)^{2}+3^{2}}}=frac{1-4+9}{sqrt{14}cdotsqrt{14}}=frac{6}{14}=frac{3}{7}.

(a⃗,b⃗^)=arccos⁡(37).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{3}{7} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(37).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{3}{7} right ).

Пример 4

Найти угол между векторами a⃗=(2;−1;−2)vec{a}=(2; -1; -2) и b⃗=(1;3;−2).vec{b}=(1; 3; -2).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=2⋅1+(−1)⋅3+(−2)⋅(−2)22+(−1)2+(−2)2⋅12+32+(−2)2=2−3+49⋅14=33⋅14=114=1414.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{2cdot1+(-1)cdot3+(-2)cdot(-2)}{sqrt{2^{2}+(-1)^{2}+(-2)^{2}}cdot sqrt{1^{2}+3^{2}+(-2)^{2}}}=frac{2-3+4}{sqrt{9}cdotsqrt{14}}=frac{3}{3cdotsqrt{14}}=frac{1}{sqrt{14}}=frac{sqrt{14}}{14}.

(a⃗,b⃗^)=arccos⁡(1414).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{sqrt{14}}{14} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(1414).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{sqrt{14}}{14} right ).

Нахождение угла между векторами с помощью векторного произведения

Синус угла между векторами можно вычислить по формуле: sin⁡(a⃗,b⃗^)=∣a⃗×b⃗∣∣a⃗∣⋅∣b⃗∣.sin(widehat{vec{a},vec{b}})=frac{left | vec{a}times vec{b} right |}{left | vec{a} right |cdotleft | vec{b} right |}.

Пример 1

Найти угол между векторами a⃗=(2;−1;2)vec{a}=(2;-1;2) и b⃗=(3;0;1).vec{b}=(3;0;1).

a⃗×b⃗=∣ijk2−12301∣=(−1−0)i−(2−6)j+(0+3)k=−i+4j+3k.vec{a}times vec{b}=begin{vmatrix}i&j&k\2&-1&2\3&0&1end{vmatrix}=(-1-0)i-(2-6)j+(0+3)k=-i+4j+3k.

∣a⃗×b⃗∣=(−1)2+42+32=1+16+9=26.left | vec{a}times vec{b} right |=sqrt{(-1)^{2}+4^{2}+3^{2}}=sqrt{1+16+9}=sqrt{26}.

∣a⃗∣=22+(−1)2+22=4+1+4=9=3.left | vec{a} right |=sqrt{2^{2}+(-1)^{2}+2^{2}}=sqrt{4+1+4}=sqrt{9}=3.

∣b⃗∣=32+02+12=9+0+1=10.left | vec{b} right |=sqrt{3^{2}+0^{2}+1^{2}}=sqrt{9+0+1}=sqrt{10}.

sin⁡(a⃗,b⃗^)=26310=132325=1335=6515.sin(widehat{vec{a},vec{b}})=frac{sqrt{26}}{3sqrt{10}}=frac{sqrt{13}sqrt{2}}{3sqrt{2}sqrt{5}}=frac{sqrt{13}}{3sqrt{5}}=frac{sqrt{65}}{15}.

(a⃗,b⃗^)=arcsin⁡(6515).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{65}}{15} right ).

Ответ: (a⃗,b⃗^)=arcsin⁡(6515).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{65}}{15} right ).

Пример 2

Найти угол между векторами a⃗=(1;1;3)vec{a}=(1;1;3) и b⃗=(0;1;1).vec{b}=(0;1;1).

a⃗×b⃗=∣ijk113011∣=(1−3)i−(1−0)j+(1−0)k=−2i−j+k.vec{a}times vec{b}=begin{vmatrix}i&j&k\1&1&3\0&1&1end{vmatrix}=(1-3)i-(1-0)j+(1-0)k=-2i-j+k.

∣a⃗×b⃗∣=(−2)2+(−1)2+12=4+1+1=6.left | vec{a}times vec{b} right |=sqrt{(-2)^{2}+(-1)^{2}+1^{2}}=sqrt{4+1+1}=sqrt{6}.

∣a⃗∣=12+12+32=1+1+9=11.left | vec{a} right |=sqrt{1^{2}+1^{2}+3^{2}}=sqrt{1+1+9}=sqrt{11}.

∣b⃗∣=02+12+12=0+1+1=2.left | vec{b} right |=sqrt{0^{2}+1^{2}+1^{2}}=sqrt{0+1+1}=sqrt{2}.

sin⁡(a⃗,b⃗^)=6112=32112=311=3311.sin(widehat{vec{a},vec{b}})=frac{sqrt{6}}{sqrt{11}sqrt{2}}=frac{sqrt{3}sqrt{2}}{sqrt{11}sqrt{2}}=frac{sqrt{3}}{sqrt{11}}=frac{sqrt{33}}{11}.

(a⃗,b⃗^)=arcsin⁡(3311).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{33}}{11} right ).

Ответ: (a⃗,b⃗^)=arcsin⁡(3311).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{33}}{11} right ).

Тест по теме “Как найти угол между двумя векторами”

Источник

Скалярное произведение векторов (далее в тексте СП). Дорогие друзья! В состав экзамена по математике входит группа задач на решение векторов. Некоторые задачи мы уже рассмотрели. Можете посмотреть их в категории «Векторы». В целом, теория векторов несложная, главное последовательно её изучить. Вычисления и действия с векторами в школьном курсе математики просты, формулы не сложные. Загляните в справочник. В этой статье мы разберём задачи на СП векторов (входят в ЕГЭ). Теперь «погружение» в теорию:

Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты его начала

И ещё:

*Длина вектора (модуль) определяется следующим образом:

Данные формулы необходимо запомнить!!!

Покажем угол между векторами:

Понятно, что он может изменяться в пределах от 0 до 180⁰ (или в радианах от 0 до Пи).

Можем сделать некоторые выводы о знаке скалярного произведения. Длины векторов имеют положительное значение, это очевидно. Значит знак скалярного произведения зависит от значения косинуса угла между векторами.

Возможны случаи:

1. Если угол между векторами острый (от 0⁰ до 90⁰), то косинус угла будет иметь положительное значение.

2. Если угол между векторами тупой (от 90⁰ до 180⁰), то косинус угла будет иметь отрицательное значение.

*При нуле градусов, то есть когда векторы имеют одинаковое направление, косинус равен единице и соответственно результат будет положительным.

При 180^о, то есть когда векторы имеют противоположные направления, косинус равен минус единице, и соответственно результат будет отрицательным.

Теперь ВАЖНЫЙ МОМЕНТ!

При 90^о, то есть когда векторы перпендикулярны друг другу, косинус равен нулю, а значит и СП равно нулю. Этот факт (следствие, вывод) используется при решение многих задач, где речь идёт о взаимном расположении векторов, в том числе и в задачах входящих в открытый банк заданий по математике.

Сформулируем утверждение: скалярное произведение равно нулю тогда и только тогда, когда данные векторы лежат на перпендикулярных прямых.

Итак, формулы СП векторов:

Если известны координаты векторов или координаты точек их начал и концов, то всегда сможем найти угол между векторами:

Рассмотрим задачи:

27724 Найдите скалярное произведение векторов a и b.

100

Скалярное произведение векторов мы можем найти по одной из двух формул:

Угол между векторами неизвестен, но мы без труда можем найти координаты векторов и далее воспользоваться первой формулой. Так как начала обоих векторов совпадают с началом координат, то координаты данных векторов равны координатам их концов, то есть

Как найти координаты вектора изложено в этой статье.

Вычисляем:

Ответ: 40

Найдём координаты векторов и воспользуемся формулой:

Чтобы найти координаты вектора необходимо из координат конца вектора вычесть соответствующие координаты его начала, значит

Вычисляем скалярное произведение:

Ответ: 40

Найдите угол между векторами a и b. Ответ дайте в градусах.

101

Пусть координаты векторов имеют вид:

Для нахождения угла между векторами используем формулу скалярного произведения векторов:

Косинус угла между векторами:

Следовательно:

Координаты данных векторов равны:

Подставим их в формулу:

Угол между векторами равен 45 градусам.

Ответ: 45

Посмотреть решение

27710. Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов АВ и AD.

102

Посмотреть решение

27719. Диагонали ромба ABCD пересекаются в точке О и равны 12 и 16. Найдите скалярное произведение векторов AB и BO.

103

Посмотреть решение

27719. Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов AB и АС.

104

Посмотреть решение

На этом всё! Успехов вам!

С уважением, Александр Крутицких.

На уроке физкультуры: — Так, парни, кто из вас курит? Честно! Не врать! Так. … значит, ты… и ты. … Понятно… Значит, так: мы с вами покурим, остальным — пять кругов по стадиону.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Источник

Определение. Углом между двумя векторами, отложенными от одной точки, называется кратчайший угол, на который нужно повернуть один из векторов вокруг своего начала до положения сонаправленности с другим вектором.

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Пример 1. Найти угол между векторами a = {3; 4} и b = {4; 3}.

Решение: Найдем скалярное произведение векторов:

a·b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

|a| = √3² + 4² = √9 + 16 = √25 = 5
|b| = √4² + 3² = √16 + 9 = √25 = 5

Найдем угол между векторами:

cos α =	a · b	=	24	=	24	= 0.96
\|a\| · \|b\|	5 · 5	25

Пример 2. Найти угол между векторами a = {7; 1} и b = {5; 5}.

Решение: Найдем скалярное произведение векторов:

a·b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

|a| = √7² + 1² = √49 + 1 = √50 = 5√2
|b| = √5² + 5² = √25 + 25 = √50 = 5√2

Найдем угол между векторами:

cos α =	a · b	=	40	=	40	=	4	= 0.8
\|a\| · \|b\|	5√2 · 5√2	50	5

Примеры вычисления угла между векторами для пространственных задач

Пример 3. Найти угол между векторами a = {3; 4; 0} и b = {4; 4; 2}.

Решение: Найдем скалярное произведение векторов:

a·b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

|a| = √3² + 4² + 0² = √9 + 16 = √25 = 5
|b| = √4² + 4² + 2² = √16 + 16 + 4 = √36 = 6

Найдем угол между векторами:

cos α =	a · b	=	28	=	14
\|a\| · \|b\|	5 · 6	15

Пример 4. Найти угол между векторами a = {1; 0; 3} и b = {5; 5; 0}.

Решение: Найдем скалярное произведение векторов:

a·b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

|a| = √1² + 0² + 3² = √1 + 9 = √10
|b| = √5² + 5² + 0² = √25 + 25 = √50 = 5√2

Найдем угол между векторами:

cos α =

a · b|a| · |b|

5√10 · 5√2

12√5

√510

= 0.1√5

Источник

Скалярное произведение векторов
Справочник по высшей математике
- - Оглавление
python — Как узнать угол между двумя векторами?
Калькулятор угла между двумя векторами
- Вектор в математике
- Что такое угол между двумя векторами?
- Как найти угол между двумя векторами
- Формулы угла между двумя векторами
- Калькулятор угла между двумя векторами — как пользоваться?
- Угол между двумя векторами — пример

Скалярное произведение векторов

Не откладывайте! ЗАГОВОРИТЕ на Английском!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2013-11-30

Чтобы найти координаты вектора, нужно из координат его конца вычесть соответствующие координаты его начала

И ещё:

*Длина вектора (модуль) определяется следующим образом:

Данные формулы необходимо запомнить!!!

Покажем угол между векторами:

Понятно, что он может изменяться в пределах от 0 до 180⁰ (или в радианах от 0 до Пи).

Возможны случаи:

1. Если угол между векторами острый (от 0⁰ до 90⁰), то косинус угла будет иметь положительное значение.

2. Если угол между векторами тупой (от 90⁰ до 180⁰), то косинус угла будет иметь отрицательное значение.

Теперь ВАЖНЫЙ МОМЕНТ!

Сформулируем утверждение: скалярное произведение равно нулю тогда и только тогда, когда данные векторы лежат на перпендикулярных прямых.

Итак, формулы СП векторов:

Рассмотрим задачи:

27724 Найдите скалярное произведение векторов a и b.

Скалярное произведение векторов мы можем найти по одной из двух формул:

Как найти координаты вектора изложено в этой статье.

Вычисляем:

Ответ: 40

Найдём координаты векторов и воспользуемся формулой:

Вычисляем скалярное произведение:

Ответ: 40

Найдите угол между векторами a и b. Ответ дайте в градусах.

Пусть координаты векторов имеют вид:

Для нахождения угла между векторами используем формулу скалярного произведения векторов:

Косинус угла между векторами:

Следовательно:

Координаты данных векторов равны:

Подставим их в формулу:

Угол между векторами равен 45 градусам.

Ответ: 45

Посмотреть решение

27710. Две стороны прямоугольника ABCD равны 6 и 8. Найдите скалярное произведение векторов АВ и AD.

Посмотреть решение

27719. Диагонали ромба ABCD пересекаются в точке О и равны 12 и 16. Найдите скалярное произведение векторов AB и BO.

Посмотреть решение

27719. Стороны правильного треугольника ABC равны 3. Найдите скалярное произведение векторов AB и АС.

Посмотреть решение

На этом всё! Успехов вам!

С уважением, Александр Крутицких.

На уроке физкультуры: — Так, парни, кто из вас курит? Честно! Не врать! Так. … значит, ты… и ты. … Понятно… Значит, так: мы с вами покурим, остальным — пять кругов по стадиону.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.

Категория: Векторы | ЕГЭ-№1Углы

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.

Справочник по высшей математике

Выгодский М.Я. Справочник по высшей математике. Изд-во «Наука». М. 1977 г.

Справочник включает весь материал, входящий в программу основного курса математики высших учебных заведений. Детальная рубрикация и подробный предметный указатель позволяют быстро получать необходимую информацию.

Книга окажет неоценимую помощь студентам, инженерам и научным работникам.

ПРЕДИСЛОВИЕ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ
§ 1. Понятие о предмете аналитической геометрии
§ 2. Координаты
§ 3. Прямоугольная система координат
§ 4. Прямоугольные координаты
§ 5. Координатные углы
§ 6. Косоугольная система координат
§ 7. Уравнение линии
§ 8. Взаимное расположение линии и точки
§ 9. Взаимное расположение двух линий
§ 10. Расстояние между двумя точками
§ 11. Деление отрезка в данном отношении
§ 11а. Деление отрезка пополам
§ 12. Определитель второго порядка
§ 13. Площадь треугольника
§ 14. Прямая линия; уравнение, разрешенное относительно ординаты (с угловым коэффициентом)
§ 15. Прямая, параллельная оси
§ 16. Общее уравнение прямой
§ 17. Построение прямой по ее уравнению
§ 18. Условие параллельности прямых
§ 19. Пересечение прямых
§ 20. Условие перпендикулярности двух прямых
§ 21. Угол между двумя прямыми
§ 22. Условие, при котором три точки лежат на одной прямой
§ 23. Уравнение прямой, проходящей через две точки
§ 24. Пучок прямых
§ 25. Уравнение прямой, проходящей через данную точку параллельно данной прямой
§ 26. Уравнение прямой, проходящей через данную точку перпендикулярно данной прямой
§ 27. Взаимное расположение прямой и пары точек
§ 28. Расстояние от точки до прямой
§ 29. Полярные параметры прямой
§ 30. Нормальное уравнение прямой
§ 31. Приведение уравнения прямой к нормальному виду
§ 32. Отрезки на осях
§ 33. Уравнение прямой в отрезках
§ 34. Преобразование координат (постановка вопроса)
§ 35. Перенос начала координат
§ 36. Поворот осей
§ 37. Алгебраические линии и их порядок
§ 38. Окружность
§ 39. Нахождение центра и радиуса окружности
§ 40. Эллипс как сжатая окружность
§ 41. Другое определение эллипса
§ 42. Построение эллипса по его осям
§ 43.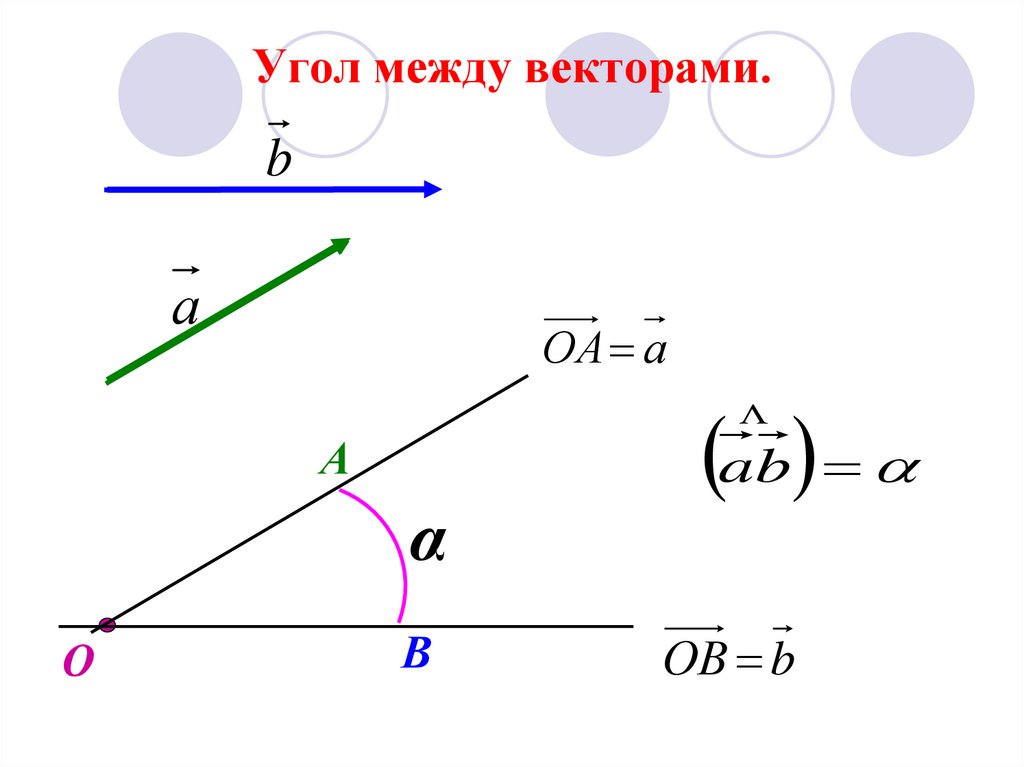 2+bx+c
§ 51. Директрисы эллипса и гиперболы
§ 52. Общее определение эллипса, гиперболы и параболы
§ 53. Конические сечения
§ 54. Диаметры конического сечения
§ 55. Диаметры эллипса
§ 56. Диаметры гиперболы
§ 57. Диаметры параболы
§ 58. Линии второго порядка
§ 59. Запись общего уравнения второй степени
§ 60. Упрощение уравнения второй степени; общие замечания
§ 61. Предварительное преобразование уравнения второй степени
§ 62. Завершающее преобразование уравнения второй степени
§ 63. О приемах, облегчающих упрощение уравнения второй степени
§ 64. Признак распадения линий второго порядка
§ 65. Нахождение прямых, составляющих распадающуюся линию второго порядка
§ 66. Инварианты уравнения второй степени
§ 67. Три типа линий второго порядка
§ 68. Центральные и нецентральные линии второго порядка
§ 69. Нахождение центра центральной линии второго порядка
§ 70. Упрощение уравнения центральной линии второго порядка
§ 71.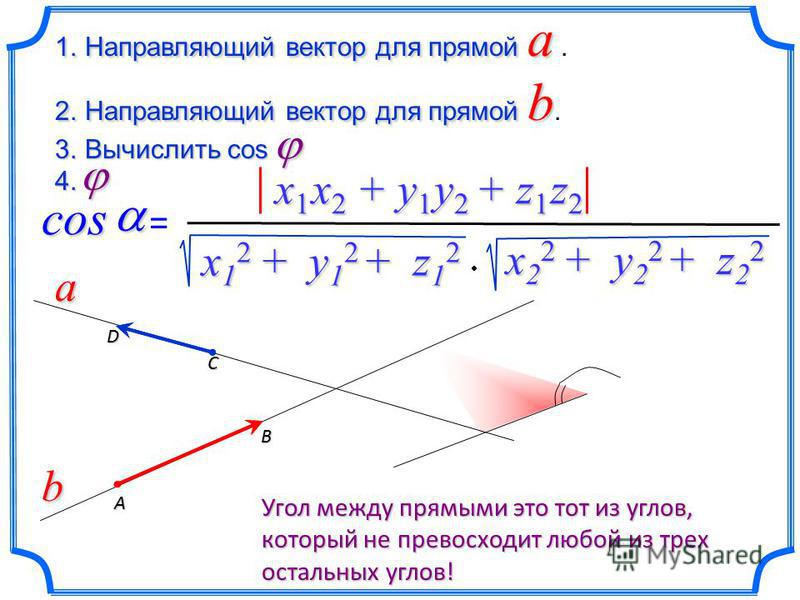 Равносторонняя гипербола как график уравнения y=k/x
§ 72. Равносторонняя гипербола как график уравнения y=(mx+n)/(px+q)
§ 73. Полярные координаты
§ 74. Связь между полярными и прямоугольными координатами
§ 75. Архимедова спираль
§ 76. Полярное уравнение прямой
§ 77. Полярное уравнение конического сечения
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ
§ 78. Понятие о векторах и скалярах
§ 79. Вектор в геометрии
§ 80. Векторная алгебра
§ 81. Коллинеарные векторы
§ 82. Нуль-вектор
§ 83. Равенство векторов
§ 84. Приведение векторов к общему началу
§ 85. Противоположные векторы
§ 86. Сложение векторов
§ 87. Сумма нескольких векторов
§ 88. Вычитание векторов
§ 89. Умножение и деление вектора на число
§ 90. Взаимная связь коллинеарных векторов (деление вектора на вектор)
§ 91. Проекция точки на ось
§ 92. Проекция вектора на ось
§ 93. Основные теоремы о проекциях вектора
§ 94. Прямоугольная система координат в пространстве
§ 95. Координаты точки
§ 96. Координаты вектора
§ 97. Выражения вектора через компоненты и через координаты
§ 98. Действия над векторами, заданными своими координатами
§ 99. Выражение вектора через радиусы-векторы его начала и конца
§ 100. Длина вектора. Расстояние между двумя точками
§ 101. Угол между осью координат и вектором
§ 102. Признак коллинеарности (параллельности) векторов
§ 103. Деление отрезка в данном отношении
§ 104. Скалярное произведение двух векторов
§ 104а. Физический смысл скалярного произведения
§ 105. Свойства скалярного произведения
§ 106. Скалярные произведения основных векторов
§ 107. Выражение скалярного произведения через координаты сомножителей
§ 108. Условие перпендикулярности векторов
§ 109. Угол между векторами
§ 110. Правая и левая системы трех векторов
§ 111. Векторное произведение двух векторов
§ 112. Свойства векторного произведения
§ 113. Векторные произведения основных векторов
§ 114. Выражение векторного произведения через координаты сомножителей
§ 115. Компланарные векторы
§ 116. Смешанное произведение
§ 117. Свойства смешанного произведения
§ 118. Определитель третьего порядка
§ 119. Выражение смешанного произведения через координаты сомножителей
§ 120. Признак компланарности в координатной форме
§ 121. Объем параллелепипеда
§ 122. Двойное векторное произведение
§ 123. Уравнение плоскости
§ 124. Особые случаи положения плоскости относительно системы координат
§ 125. Условие параллельности плоскостей
§ 126. Условие перпендикулярности плоскостей
§ 127. Угол между двумя плоскостями
§ 128. Плоскость, проходящая через данную точку параллельно данной плоскости
§ 129. Плоскость, проходящая через три точки
§ 130. Отрезки на осях
§ 131. Уравнение плоскости в отрезках
§ 132. Плоскость, проходящая через две точки перпендикулярно данной плоскости
§ 133. Плоскость, проходящая через данную точку перпендикулярно двум плоскостям
§ 134. Точка пересечения трех плоскостей
§ 135. Взаимное расположение плоскости и пары точек
§ 136. Расстояние от точки до плоскости
§ 137. Полярные параметры плоскости
§ 138. Нормальное уравнение плоскости
§ 139. Приведение уравнения плоскости к нормальному виду
§ 140. Уравнения прямой в пространстве
§ 141. Условие, при котором два уравнения первой степени представляют прямую
§ 142. Пересечение прямой с плоскостью
§ 143. Направляющий вектор
§ 144. Углы между прямой и осями координат
§ 145. Угол между двумя прямыми
§ 146. Угол между прямой и плоскостью
§ 147. Условия параллельности и перпендикулярности прямой и плоскости
§ 148. Пучок плоскостей
§ 149. Проекции прямой на координатные плоскости
§ 150. Симметричные уравнения прямой
§ 151. Приведение уравнений прямой к симметричному виду
§ 152. Параметрические уравнения прямой
§ 153. Пересечение плоскости с прямой, заданной параметрически
§ 154. Уравнения прямой, проходящей через две данные точки
§ 155. Уравнение плоскости, проходящей через данную точку перпендикулярно данной прямой
§ 156. Уравнения прямой, проходящей через данную точку перпендикулярно данной плоскости
§ 157. Уравнение плоскости, проходящей через данную точку и данную прямую
§ 158. Уравнение плоскости, проходящей через данную точку и параллельной двум данным прямым
§ 159. Уравнение плоскости, проходящей через данную прямую и параллельной другой данной прямой
§ 160. Уравнение плоскости, проходящей через данную прямую и перпендикулярной данной плоскости
§ 161. Уравнения перпендикуляра, опущенного из данной точки на данную прямую
§ 162. Длина перпендикуляра, опущенного из данной точки на данную прямую
§ 163. Условие, при котором две прямые пересекаются или лежат в одной плоскости
§ 164. Уравнения общего перпендикуляра к двум данным прямым
§ 165. Кратчайшее расстояние между двумя прямыми
§ 165а. Правые и левые пары прямых
§ 166. Преобразование координат
§ 167. Уравнение поверхности
§ 168. Цилиндрические поверхности, у которых образующие параллельны одной из осей координат
§ 169. Уравнения линии
§ 170. Проекция линии на координатную плоскость
§ 171. Алгебраические поверхности и их порядок
§ 172. Сфера
§ 173. Эллипсоид
§ 174. Однополостный гиперболоид
§ 175. Двуполостный гиперболоид
§ 176. Конус второго порядка
§ 177. Эллиптический параболоид
§ 178. Гиперболический параболоид
§ 179. Перечень поверхностей второго порядка
§ 180. Прямолинейные образующие поверхностей второго порядка
§ 181. Поверхности вращения
§ 182. Определители второго и третьего порядков
§ 183. Определители высших порядков
§ 184. Свойства определителей
§ 185. Практический прием вычисления определителей
§ 186. Применение определителей к исследованию и решению системы уравнений
§ 187. Два уравнения с двумя неизвестными
§ 188. Два уравнения с двумя неизвестными
§ 189. Однородная система двух уравнений с тремя неизвестными
§ 190. Два уравнения с двумя неизвестными
§ 190а. Система n уравнений с n неизвестными
ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОГО АНАЛИЗА
§ 192. Рациональные числа
§ 193. Действительные (вещественные) числа
§ 194. Числовая ось
§ 195. Переменные и постоянные величины
§ 196. Функция
§ 197. Способы задания функции
§ 198. Область определения функции
§ 199. Промежуток
§ 200. Классификация функций
§ 201. Основные элементарные функции
§ 202. Обозначение функции
§ 203. Предел последовательности
§ 204. Предел функции
§ 205. Определение предела функции
§ 206. Предел постоянной величины
§ 207. Бесконечно малая величина
§ 208. Бесконечно большая величина
§ 209. Связь между бесконечно большими и бесконечно малыми величинами
§ 210. Ограниченные величины
§ 211. Расширение понятия предепа
§ 212. Основные свойства бесконечно малых величин
§ 213. Основные теоремы о пределах
§ 214. Число е
§ 215. Предел sinx/x при x стремящемся к 0
§ 216. Эквивалентные бесконечно малые величины
§ 217. Сравнение бесконечно малых величин
§ 217а. Приращение переменной величины
§ 218. Непрерывность функции в точке
§ 219. Свойства функций, непрерывных в точке
§ 219а. Односторонний предел; скачок функции
§ 220. Непрерывность функции на замкнутом промежутке
§ 221. Свойства функций, непрерывных на замкнутом промежутке
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 223. Скорость
§ 224. Определение производной функции
§ 225. Касательная
§ 226. Производные некоторых простейших функций
§ 227. Свойства производной
§ 228. Дифференциал
§ 229. Механический смысл дифференциала
§ 230. Геометрический смысл дифференциала
§ 231. Дифференцируемые функции
§ 232. Дифференциалы некоторых простейших функций
§ 233. Свойства дифференциала
§ 234. Инвариантность выражения f'(x)dx
§ 235. Выражение производной через дифференциалы
§ 236. Функция от функции (сложная функция)
§ 237. Дифференциал сложной функции
§ 238. Производная сложной функции
§ 239. Дифференцирование произведения
§ 240. Дифференцирование частного (дроби)
§ 241. Обратная функция
§ 242. Натуральные логарифмы
§ 243. Дифференцирование логарифмической функции
§ 244. Логарифмическое дифференцирование
§ 245. Дифференцирование показательной функции
§ 246. Дифференцирование тригонометрических функций
§ 247. Дифференцирование обратных тригонометрических функций
§ 247а. Некоторые поучительные примеры
§ 248. Дифференциал в приближенных вычислениях
§ 249. Применение дифференциала к оценке погрешности формул
§ 250. Дифференцирование неявных функций
§ 251. Параметрическое задание линии
§ 252. Параметрическое задание функции
§ 253. Циклоида
§ 254. Уравнение касательной к плоской линии
§ 254а. Касательные к кривым второго порядка
§ 255. Уравнение нормали
§ 256. Производные высших порядков
§ 257. Механический смысл второй производной
§ 258. Дифференциалы высших порядков
§ 259. Выражение высших производных через дифференциалы
§ 260. Высшие производные функций, заданных параметрически
§ 261. Высшие производные неявных функций
§ 262. Правило Лейбница
§ 263. Теорема Ролля
§ 264. Теорема Лагранжа о среднем значении
§ 265. Формула конечных приращений
§ 266. Обобщенная теорема о среднем значении (Коши)
§ 267. Раскрытие неопределенности вида 0/0
§ 268. Раскрытие неопределенности вида бесконесность на бесконечность
§ 269. Неопределенные выражения других видов
§ 270. Исторические сведения о формуле Тейлора
§ 271. Формула Тейлора
§ 272. Применение формулы Тейлора к вычислению значений функции
§ 273. Возрастание и убывание функции
§ 274. Признаки возрастания и убывания функции в точке
§ 274а. Признаки возрастания и убывания функции в промежутке
§ 275. Максимум и минимум
§ 276. Необходимое условие максимума и минимума
§ 277. Первое достаточное условие максимума и минимума
§ 278. Правило нахождения максимумов и минимумов
§ 279. Второе достаточное условие максимума и минимума
§ 280. Нахождение наибольшего и наименьшего значений функции
§ 281. Выпуклость плоских кривых; точка перегиба
§ 282. Сторона вогнутости
§ 283. Правило для нахождения точек перегиба
§ 284. Асимптоты
§ 285. Нахождение асимптот, параллельных координатным осям
§ 286. Нахождение асимптот, не параллельных оси ординат
§ 287. Приемы построения графиков
§ 288. Решение уравнений. Общие замечания
§ 289. Решение уравнений. Способ хорд
§ 290. Решение уравнений. Способ касательных
§ 291. Комбинированный метод хорд и касательных
ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
§ 293. Первообразная функция
§ 294. Неопределенный интеграл
§ 295. Геометрический смысл интегрирования
§ 296. Вычисление постоянной интегрирования по начальным данным
§ 297. Свойства неопределенного интеграла
§ 298. Таблица интегралов
§ 299. Непосредственное интегрирование
§ 300. Способ подстановки (интегрирование через вспомогательную переменную)
§ 301. Интегрирование по частям
§ 302. Интегрирование некоторых тригонометрических выражений
§ 303. Тригонометрические подстановки
§ 304. Рациональные функции
§ 304а. Исключение целой части
§ 305. О приемах интегрирования рациональных дробей
§ 306. Интегрирование простейших рациональных дробей
§ 307. Интегрирование рациональных функций (общий метод)
§ 308. О разложении многочлена на множители
§ 309. Об интегрируемости в элементарных функциях
§ 310. Некоторые интегралы, зависящие от радикалов
§ 311. Интеграл от биномиального дифференциала
§ 312. Интегралы вида …
§ 313. Интегралы вида S R(sinx, cosx)dx
§ 314. Определенный интеграл
§ 315. Свойства определенного интеграла
§ 316. Геометрический смысл определенного интеграла
§ 317. Механический смысл определенного интеграла
§ 318. Оценка определенного интеграла
§ 318а. Неравенство Буняковского
§ 319. Теорема о среднем интегрального исчисления
§ 320. Определенный интеграл как функция верхнего предела
§ 321. Дифференциал интеграла
§ 322. Интеграл дифференциала. Формула Ньютона — Лейбница
§ 323. Вычисление определенного интеграла с помощью неопределенного
§ 324. Определенное интегрирование по частям
§ 325. Способ подстановки в определенном интеграле
§ 326. О несобственных интегралах
§ 327. Интегралы с бесконечными пределами
§ 328. Интеграл функции, имеющей разрыв
§ 329. О приближенном вычислении интеграла
§ 330. Формулы прямоугольников
§ 331. Формула трапеций
§ 332. Формула Симпсона (параболических трапеций)
§ 333. Площади фигур, отнесенных к прямоугольным координатам
§ 334. Схема применения определенного интеграла
§ 335. Площади фигур, отнесенных к полярным координатам
§ 336. Объем тела по поперечным сечениям
§ 337. Объем тела вращения
§ 338. Длина дуги плоской линии
§ 339. Дифференциал дуги
§ 340. Длина дуги и ее дифференциал в полярных координатах
§ 341. Площадь поверхности вращения
ОСНОВНЫЕ СВЕДЕНИЯ О ПЛОСКИХ И ПРОСТРАНСТВЕННЫХ ЛИНИЯХ
§ 342.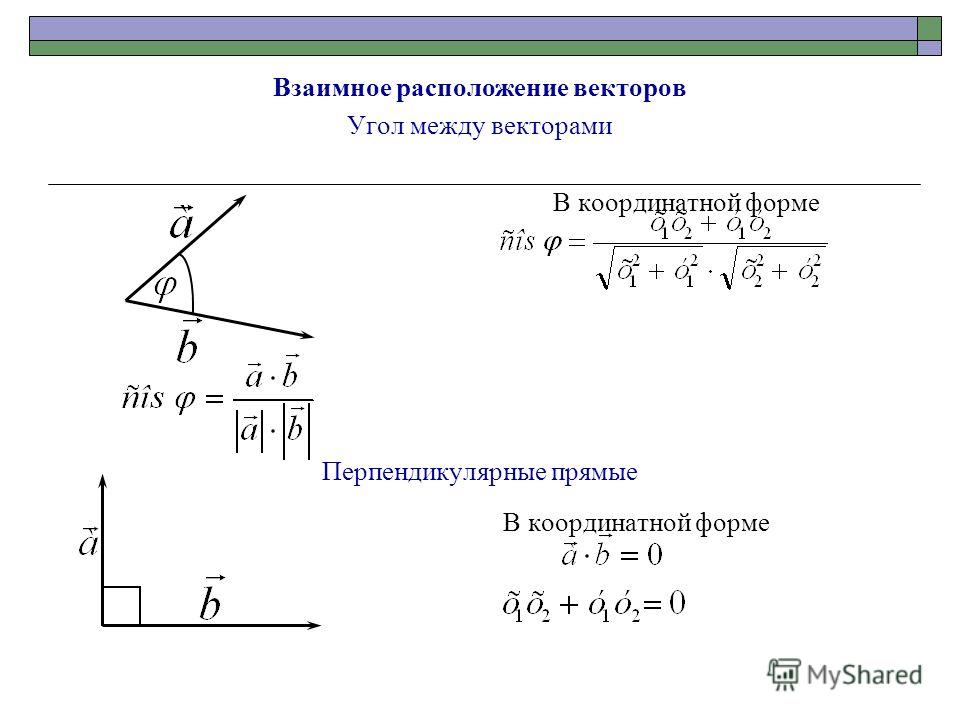 Кривизна
§ 343. Центр, радиус и круг кривизны плоской линии
§ 344. Формулы для кривизны, радиуса и центра кривизны плоской линии
§ 345. Эволюта плоской линии
§ 346. Свойства эволюты плоской линии
§ 347. Развертка (эвольвента) плоской линии
§ 348. Параметрическое задание пространственной линии
§ 349. Винтовая линия
§ 350. Длина дуги пространственной линии
§ 351. Касательная к пространственной линии
§ 352. Нормальная плоскость
§ 353. Вектор-функция скалярного аргумента
§ 354. Предел вектор-функции
§ 355. Производная вектор-функции
§ 356. Дифференциал вектор-функции
§ 357. Свойства производной и дифференциала вектор-функции
§ 358. Соприкасающаяся плоскость
§ 359. Главная нормаль. Сопутствующий трехгранник
§ 360. Взаимное расположение линии и плоскости
§ 361. Основные векторы сопутствующего трехгранника
§ 362. Центр, ось и радиус кривизны пространственной линии
§ 363. Формулы для кривизны, радиуса и центра кривизны пространственной линии
§ 364. О знаке кривизны
§ 365. Кручение
РЯДЫ
§ 367. Определение ряда
§ 368. Сходящиеся и расходящиеся ряды
§ 369. Необходимое условие сходимости ряда
§ 370. Остаток ряда
§ 371. Простейшие действия над рядами
§ 372. Положительные ряды
§ 373. Сравнение положительных рядов
§ 374. Признак Даламбера для положительного ряда
§ 375. Интегральный признак сходимости
§ 376. Знакопеременный ряд. Признак Лейбница
§ 377. Абсолютная и условная сходимость
§ 378. Признак Даламбера для произвольного ряда
§ 379. Перестановка членов ряда
§ 380. Группировка членов ряда
§ 381. Умножение рядов
§ 382. Деление рядов
§ 383. Функциональный ряд
§ 384. Область сходимости функционального ряда
§ 385. О равномерной и неравномерной сходимости
§ 386. Определение равномерной и неравномерной сходимости
§ 387. Геометрический смысл равномерной и неравномерной сходимости
§ 388. Признак равномерной сходимости; правильные ряды
§ 389. Непрерывность суммы ряда
§ 390. Интегрирование рядов
§ 391. Дифференцирование рядов
§ 392. Степенной ряд
§ 393. Промежуток и радиус сходимости степенного ряда
§ 394. Нахождение радиуса сходимости
§ 395. Область сходимости ряда, расположенного по степеням х – х0
§ 396. Теорема Абеля
§ 397. Действия со степенными рядами
§ 398. Дифференцирование и интегрирование степенного ряда
§ 399. Ряд Тейлора
§ 400. Разложение функции в степенной ряд
§ 401. Разложение элементарных функций в степенные ряды
§ 402. Применение рядов к вычислению интегралов
§ 403. Гиперболические функции
§ 404. Обратные гиперболические функции
§ 405. Происхождение наименований гиперболических функций
§ 406. О комплексных числах
§ 407. Комплексная функция действительного аргумента
§ 408. Производная комплексной функции
§ 409. Возведение положительного числа в комплексную степень
§ 410. Формула Эйлера
§ 411. Тригонометрический ряд
§ 412. Исторические сведения о тригонометрических рядах
§ 413.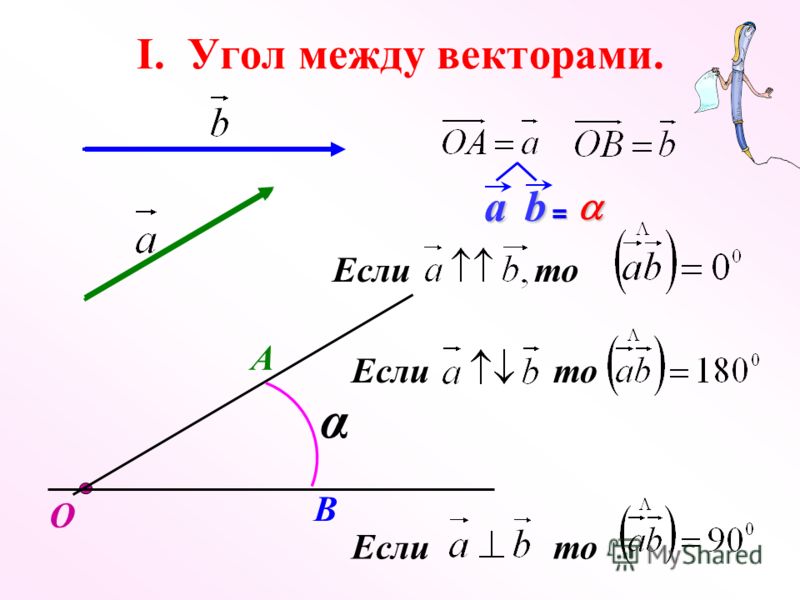 Ортогональность системы функций cos nx, sin nx
§ 414. Формулы Эйлера-Фурье
§ 415. Ряд Фурье
§ 416. Ряд Фурье для непрерывной функции
§ 417. Ряд Фурье для четной и нечетной функции
§ 418. Ряд Фурье для разрывной функции
ДИФФЕРЕНЦИРОВАНИЕ И ИНТЕГРИРОВАНИЕ ФУНКЦИЙ НЕСКОЛЬКИХ АРГУМЕНТОВ
§ 420. Функция трех и большего числа аргументов
§ 421. Способы задания функций нескольких аргументов
§ 422. Предел функции нескольких аргументов
§ 424. Непрерывность функции нескольких аргументов
§ 425. Частные производные
§ 426. Геометрический смысл частных производных для случая двух аргументов
§ 427. Полное и частное приращения
§ 428. Частный дифференциал
§ 429. О выражении частной производной через дифференциал
§ 430. Полный дифференциал
§ 431. Геометрический смысл полного дифференциала (случай двух аргументов)
§ 432. Инвариантность выражения … полного дифференциала
§ 433. Техника дифференцирования
§ 434. Дифференцируемые функции
§ 435. Касательная плоскость и нормаль к поверхности
§ 436. Уравнение касательной плоскости
§ 437. Уравнения нормали
§ 438. Дифференцирование сложной функции
§ 439. Замена прямоугольных координат полярными
§ 440. Формулы для производных сложной функции
§ 441. Полная производная
§ 442. Дифференцирование неявной функции нескольких переменных
§ 443. Частные производные высших порядков
§ 444. Полные дифференциалы высших порядков
§ 445. Техника повторного дифференцирования
§ 446. Условное обозначение дифференциалов
§ 447. Формула Тейлора для функции нескольких аргументов
§ 448. Экстремум (максимум и минимум) функции нескольких аргументов
§ 449. Правило нахождения экстремума
§ 450. Достаточные условия экстремума (случай двух аргументов)
§ 451. Двойной интеграл
§ 452. Геометрический смысл двойного интеграла
§ 453. Свойства двойного интеграла
§ 454. Оценка двойного интеграла
§ 455. Вычисление двойного интеграла (простейший случай)
§ 456. Вычисление двойного интеграла (общий случай)
§ 457. Функция точки
§ 458. Выражение двойного интеграла через полярные координаты
§ 459. Площадь куска поверхности
§ 460. Тройной интеграл
§ 461. Вычисление тройного интеграла (простейший случай)
§ 462. Вычисление тройного интеграла (общий случай)
§ 463. Цилиндрические координаты
§ 464. Выражение тройного интеграла через цилиндрические координаты
§ 465. Сферические координаты
§ 466. Выражение тройного интеграла через сферические координаты
§ 467. Схема применения двойного и тройного интегралов
§ 468. Момент инерции
§ 471. Криволинейный интеграл
§ 472. Механический смысл криволинейного интеграла
§ 473. Вычисление криволинейного интеграла
§ 474. Формула Грина
§ 475. Условие, при котором криволинейный интеграл не зависит от пути
§ 476. Другая форма условия предыдущего параграфа
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
§ 478. Уравнение первого порядка
§ 479. Геометрический смысл уравнения первого порядка
§ 480. Изоклины
§ 481. Частное и общее решения уравнения первого порядка
§ 482. Уравнения с разделенными переменными
§ 483. Разделение переменных. Особое решение
§ 484. Уравнение в полных дифференциалах
§ 484а. Интегрирующий множитель
§ 485. Однородное уравнение
§ 486. Линейное уравнение первого порядка
§ 487. Уравнение Клеро
§ 488. Огибающая
§ 489. Об интегрируемости дифференциальных уравнений
§ 490. Приближенное интегрирование уравнений первого порядка по методу Эйлера
§ 491. Интегрирование дифференциальных уравнений с помощью рядов
§ 492. О составлении дифференциальных уравнений
§ 493. Уравнение второго порядка
§ 494. Уравнение n-го порядка
§ 495. Случаи понижения порядка
§ 496. Линейное уравнение второго порядка
§ 497. Линейное уравнение второго порядка с постоянными коэффициентами
§ 498. Линейное уравнение второго порядка с постоянными коэффициентами без правой части
§ 498а. Связь между случаями 1 и 3 § 498
§ 499. Линейное уравнение второго порядка с постоянными коэффициентами с правой частью
§ 500. Линейные уравнения любого порядка
§ 501. Метод вариации постоянных
§ 502. Системы дифференциальных уравнений. Линейные системы
НЕКОТОРЫЕ ЗАМЕЧАТЕЛЬНЫЕ КРИВЫЕ
§ 503. Строфоида
§ 504. Циссоида Диокла
§ 505. Декартов лист
§ 506. Верзьера Аньези
§ 507. Конхоида Никомеда
§ 508. Улитка Паскаля; кардиоида
§ 509. Линия Кассини
§ 510. Лемниската Бернулли
§ 511. Архимедова спираль
§ 512. Эвольвента (развертка) круга
§ 513. Логарифмическая спираль
§ 514. Циклоиды
§ 515. Эпициклоиды и гипоциклоиды
§ 516. Трактриса
§ 517. Цепная линия

python — Как узнать угол между двумя векторами?

В общем, угол вектора (x, y) можно вычислить с помощью math.atan2(y, x) . Вектор может быть задан двумя точками (x1, y1) и (x2, y2) на линии. Следовательно, угол линии равен math. atan2(y2-y1, x2-x1) .
Имейте в виду, что ось Y необходимо перевернуть ( -y соответственно y1-y2 ), потому что ось Y обычно указывает вверх, но в системе координат PyGame ось Y указывает вниз. Единица угла в Python 9Модуль 0005 math — это радианы, но единицей измерения угла в функциях PyGame, таких как pygame.transform.rotate() , является градус. Следовательно, угол должен быть преобразован из радианов в градусы с помощью math.degrees :

 import math
определение угла_вектора (х, у):
    вернуть math.степени(math.atan2(-y, x))
определение угла_линии (x1, y1, x2, y2):
    вернуть math.степени(math.atan2(-(y2-y1), x2-x1))

Это можно упростить, используя метод angle_to из pygame.math.Vector2 объект. Этот метод вычисляет угол между двумя векторами в системе координат PyGame в градусах. Поэтому нет необходимости переворачивать ось Y и преобразовывать радианы в градусы. Просто вычислите угол между вектором и (1, 0) :

 def angle_of_vector(x, y):
    вернуть pygame. math.Vector2 (x, y).angle_to ((1, 0))
определение угла_линии (x1, y1, x2, y2):
    вернуть angle_of_vector (x2-x1, y2-y1)

Минимальный пример:

 import pygame
импортировать математику
определение угла_вектора (х, у):
    #return math.степени(math.atan2(-y, x)) # 1: с math.atan
    return pygame.math.Vector2(x, y).angle_to((1, 0)) # 2: с pygame.math.Vector2.angle_to
    
определение угла_линии (x1, y1, x2, y2):
    #return math.степени(math.atan2(-y1-y2, x2-x1)) # 1: math.atan
    вернуть angle_of_vector(x2-x1, y2-y1) # 2: pygame.math.Vector2.angle_to
    
pygame.init()
окно = pygame.display.set_mode((400, 400))
часы = pygame.time.Clock()
шрифт = pygame.font.SysFont (нет, 50)
угол = 0
радиус = 150
vec = (радиус, 0)
запустить = Истина
во время работы:
    часы.тик(60)
    для события в pygame.event.get():
        если event.type == pygame.ВЫЙТИ:
            запустить = Ложь
    cpt = окно.get_rect().центр
    pt = cpt[0] + vec[0], cpt[1] + vec[1]
    угол = угол_вектора(*vec)
    окно. заполнить((255, 255, 255))
    pygame.draw.circle (окно, (0, 0, 0), cpt, радиус, 1)
    pygame.draw.line (окно, (0, 255, 0), cpt, (cpt [0] + радиус, cpt [1]), 3)
    pygame.draw.line (окно, (255, 0, 0), cpt, pt, 3)
    text_surf = font.render(str(round(angle/5)*5) + "°", True, (255, 0, 0))
    text_surf.set_alpha(127)
    window.blit(text_surf, text_surf.get_rect(нижний левый = (cpt[0]+20, cpt[1]-20)))
    pygame.display.flip()
    угол = (угол + 1)% 360
    vec = радиус * math.cos(угол*math.pi/180), радиус * -math.sin(угол*math.pi/180)
pygame.выйти()
Выход()

angle_to можно использовать для вычисления угла между двумя векторами или линиями:

 def angle_between_vectors(x1, y1, x2, y2):
    вернуть pygame.math.Vector2 (x1, y1).angle_to ((x2, y2))

Минимальный пример:

 импорт pygame
импортировать математику
def angle_between_vectors (x1, y1, x2, y2):
    вернуть pygame.math.Vector2 (x1, y1).angle_to ((x2, y2))
определение угла_вектора (х, у):
    вернуть pygame. math.Vector2 (x, y).angle_to ((1, 0))
    
pygame.init()
окно = pygame.display.set_mode((400, 400))
часы = pygame.time.Clock()
шрифт = pygame.font.SysFont (нет, 50)
угол = 0
радиус = 150
vec1 = (радиус, 0)
vec2 = (радиус, 0)
запустить = Истина
во время работы:
    часы.тик(60)
    для события в pygame.event.get():
        если event.type == pygame.ВЫЙТИ:
            запустить = Ложь
    cpt = окно.get_rect().центр
    pt1 = cpt[0] + vec1[0], cpt[1] + vec1[1]
    pt2 = cpt[0] + vec2[0], cpt[1] + vec2[1]
    угол = угол_между_векторами(*vec2, *vec1)
    окно.заполнить((255, 255, 255))
    pygame.draw.circle (окно, (0, 0, 0), cpt, радиус, 1)
    pygame.draw.line (окно, (0, 255, 0), cpt, pt1, 3)
    pygame.draw.line(окно, (255, 0, 0), cpt, pt2, 3)
    text_surf = font.render(str(round(angle/5)*5) + "°", True, (255, 0, 0))
    text_surf.set_alpha(127)
    window.blit(text_surf, text_surf.get_rect(нижний левый = (cpt[0]+20, cpt[1]-20)))
    pygame.display.flip()
    угол1 = (угол_вектора(*vec1) + 1/3)% 360
    vec1 = радиус * math. cos(угол1*math.pi/180), радиус * -math.sin(угол1*math.pi/180)
    угол2 = (угол_вектора(*vec2) + 1)% 360
    vec2 = радиус * math.cos(угол2*math.pi/180), радиус * -math.sin(угол2*math.pi/180)
pygame.выйти()
Выход()

Калькулятор угла между двумя векторами

Калькулятор угла между двумя векторами — это бесплатный инструмент, простой в использовании, он очень быстро вычисляет угол между двумя векторами. Однако, если вас интересует не только результат, но и получение знаний, чувствуйте себя как дома и ознакомьтесь с содержанием на этой странице, а также на нашем сайте.

Наши предложения для закладки фундамента в линейной алгебре: Калькулятор векторной проекции, Калькулятор векторной величины, Калькулятор единичного вектора, Калькулятор векторного произведения и, конечно же, эта статья. Также ознакомьтесь с другими нашими калькуляторами и оставьте отзыв. Нам всегда приятно узнать о ваших впечатлениях о нашей работе.

Многие студенты подходят к линейной алгебре со страхом и разочарованием. Если вы один из них, вот почему это происходит с вами. Не новость, что первый взгляд на законы и теоремы, особенно на рисунки, относящиеся к линейной алгебре, сбивает с толку. Точнее, от всех этих символов, новых терминов и запутанных векторов у вас затуманивается голова, и вы теряете интерес даже к попыткам ее выучить.

Что, если мы пообещаем, что эта статья предоставит вам все необходимые детали, оставаясь при этом легко читаемой? Мы думаем, что вам бы это понравилось. Именно поэтому команда калькуляторов CalCon решила вашу проблему. Решение, о котором мы говорим, — это калькулятор, за которым следует статья.

Вектор в математике

Чтобы выполнить наше обещание, во-первых, мы объясним, что представляет собой вектор в математике. Термин «вектор » увидел свет в математике, чтобы различать величины в природе, имеющие величину и направление. Напротив, те, у которых есть только величина, называются скаляров . Таким образом, векторные величины определяются двумя или более параметрами.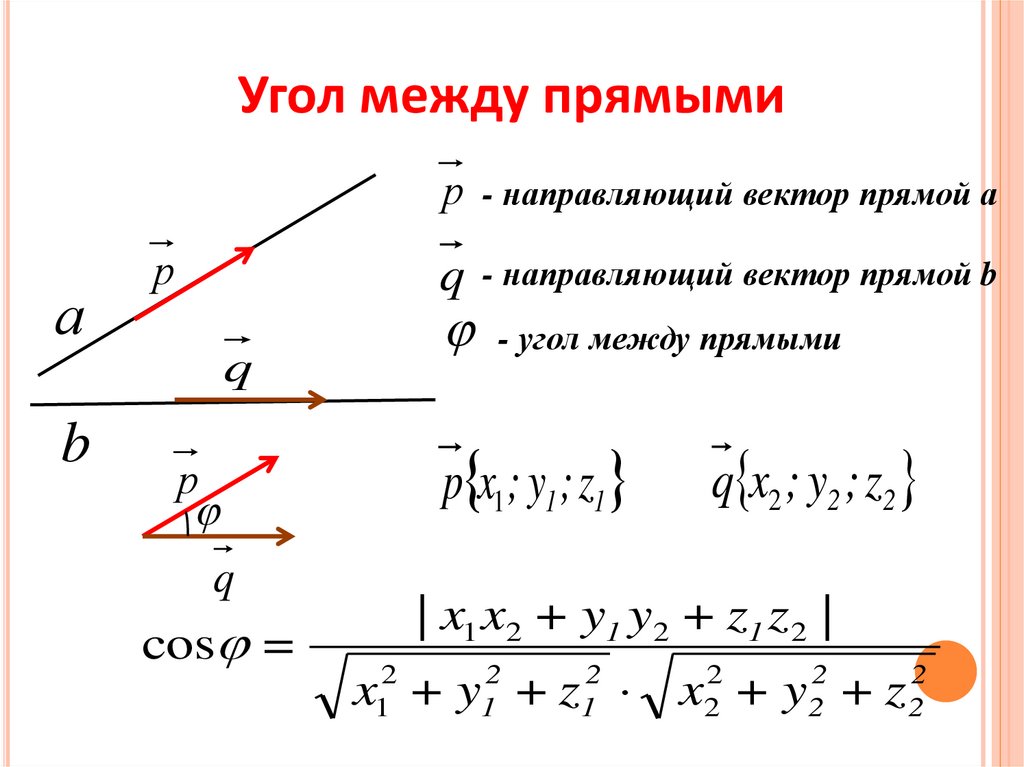

Наиболее распространенные примеры связаны с геометрией пространства, где вектор, лежащий на прямой линии, определяется направлением и величиной. Указывающая стрелка определяет свое направление вдоль прямой линии, а ее длина пропорциональна ее величине.

В заключение, вектор в n-мерном пространстве описывается n параметрами (где n — любое число). Но давайте посмотрим на евклидов вектор, у которого есть величина и направление, и, согласно предыдущему предложению, это двумерный вектор. Этот вектор обычно представляет собой отрезок линии с определенным направлением или, графически, стрелку, соединяющую начальную точку (А) с конечной точкой (В). Обозначается как vec{AB}.

Если в любом случае это было недостаточно ясно, мы считаем, что Пример из реальной жизни подстегнет ваше воображение и поможет понять термины, упомянутые ранее. Для иллюстрации представим себе бегуна, стоящего на стартовой линии и готового пробежать марафон на пятьдесят метров по прямой трассе.

Так как этот маршрут может быть продлен в обоих направлениях, при этом образуя прямую линию , часть, выбранная в качестве длины марафона, лежит на этой прямой. Таким образом, линиями старта и финиша являются стартовых (А) и конечных (В) точек вектора. Итак, величина вектора — это длина маршрута, а направление определяется направлением бегуна, бегущего к финишу.

Что такое угол между двумя векторами?

Угол между двумя векторами — это векторный угол, образованный соединением хвостов двух векторов. Важно подчеркнуть, что угол образуется только путем соединения векторов решками, а не решками или решка-голова. Что касается возможности того, что это может сбивать с толку, мы покажем это на картинке.

Угол между двумя векторами

Также важно отметить, что для соединения хвостов векторов мы используем параллельный сдвиг.

Как найти угол между двумя векторами

Нахождение угла между двумя векторами будет описано в следующих шагах:

Мы начнем с нахождения скалярного произведения наших векторов:

 vec{a } cdot vec{b} = |vec{a}| cdot|vec{b}| cdot cos(alpha)

Скалярное произведение двух векторов является скалярным произведением двух векторов и применимо только к набору векторов с одинаковым числом измерений. Символ скалярного произведения — толстая точка. 9{2}}}

Кроме того, если вы знаете начальную и конечную точки векторов, вам необходимо преобразовать их в стандартную нотацию векторов. Например, если вектор описывается начальной точкой A=[x_1, y_1] и конечной точкой B=[x_2, y_2] , то вектор vec {a} может быть выражен как: vec {a} = [ x_2 — x_1, y_2 — y_1]

Формулы угла между двумя векторами

Для лучшего понимания и работы с формулами в этом параграфе мы разделим формулы для угла между двумя векторами в 2D и 3D пространстве. 9{2}}}

Если вектор описывается начальной и конечной точкой , то сначала нужно получить их координаты:

Вектор в двумерном пространстве

Для вектора vec {a} : A = [x_ {1}, y_{1}], B = [x_{2}, y_{2}], поэтому вектор vec {a} = [x_{2} — x_{1}, y_{2} — y_{ 1}]

Для вектора vec {b}: C = [x_{3}, y_{3}] , D = [x_{4}, y_{4}] , поэтому вектор vec {b} = [ x_{4} — x_{3}, y_{4} — y_{3}]

Теперь подставим эти координаты в формулу угла между двумя векторами: 9{2}}}

Если геометрия вектора описывается начальной и конечной точкой , то сначала нужно получить их координаты:

Вектор в трехмерном пространстве

Для вектора vec {a}: A = [ x_1, y_1, z_1], B = [x_2, y_2, z_2] , поэтому vec {a} = [x_2 — x_1, y_2 — y_1, z_2 — z_1]

Для вектора vec {b}: C = [ x_3, y_3, z_3], D = [x_4, y_4, z_4] , поэтому vec {b} = [x_4 — x_3, y_4 — y_3, z_4 — z_3]

Как только мы познакомимся с координатами наших векторов, подставляем их в формулу угла между двумя векторами: 9{2}}}

Калькулятор угла между двумя векторами — как пользоваться?

Учитывая сложность задачи, мы преуспели в том, чтобы сделать этот калькулятор максимально простым в использовании. Соответственно, следующие инструкции также нетребовательны и удобоваримы для новичка:

В самом начале выберите, находится ли вектор в 2D или 3D пространстве,
Теперь выберите один из вариантов для каждого вектора: вектор представлен с координатами или по начальной и конечной точкам.
После этого введите в указанные поля калькулятора значения, описывающие положение векторов.
После выполнения последнего шага калькулятор измерит угол между двумя векторами, и появится результат.

Угол между двумя векторами — пример

В этом примере нам нужно найти угол между двумя векторами vec{a}=[7,1] и vec{b}=[5,5] . Чтобы получить угол между двумя векторами, нам нужно пройти следующие шаги:

9{2}}=5кв{2}

И, наконец, угол между векторами:

угол = arccos frac { vec {a} cdot vec {b}} }{| vec {a} | cdot |vec{b}|}=arccosfrac{40}{5sqrt{2} cdot 5sqrt{2}}=36,87 градус

Использование калькулятора угла между двумя векторами избавляет вас от ручных расчетов и в то же время является простым в использовании.

Источник

Содержание:

Формула
Примеры вычисления угла между векторами

Формула

Чтобы найти угол $phi$ между векторами нужно вначале найти
косинус угла, а затем от него найти арккосинус, то есть:

$$phi=arccos (cos phi)$$

Косинус угла между векторами равен
скалярному произведению этих векторов, деленному на произведение их
длин.
В случае если векторы заданны на плоскости и имеют координаты
$bar{a}=left(a_{x} ; a_{y}right)$, $bar{b}=left(b_{x} ; b_{y}right)$, то косинус между ними вычисляется по формуле:

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$$

В случае, если векторы заданы в пространстве, то есть
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то косинус угла между ними равен:

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$

Примеры вычисления угла между векторами

Пример

Задание. Найти угол $phi$ между векторами
$bar{a}=(1 ; 3)$ и $bar{b}=(4 ; 2)$

Решение. Сначала по формуле

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}}{sqrt{a_{x}^{2}+a_{y}^{2}} sqrt{b_{x}^{2}+b_{y}^{2}}}$$

найдем косинус угла между заданными векторами:

$$begin{aligned} cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=& frac{1 cdot 4+3 cdot 2}{sqrt{1^{2}+3^{2}} cdot sqrt{4^{2}+2^{2}}}=frac{4+6}{sqrt{1+9} cdot sqrt{16+4}}=\ &=frac{10}{sqrt{10} cdot sqrt{20}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2}} end{aligned}$$

Тогда искомый угол равен

$$phi=arccos left(frac{sqrt{2}}{2}right)=45^{circ}$$

Ответ. $phi=45^{circ}$

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример

Задание. Найти угол $phi$ между векторами
$bar{a}=(8 ;-7 ;-2)$ и $bar{b}=(7 ;-11 ; 8)$

Решение. Найдем сначала косинус угла между заданными векторами, для этого воспользуемся формулой

$$cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}}$$

Подставляя координаты векторов
$bar{a}$ и $bar{b}$, получим

$$begin{aligned} cos phi=frac{(bar{a}, bar{b})}{|bar{a}| cdot|bar{b}|}=frac{8 cdot 7+(-7) cdot(-11)+(-2) cdot 8}{sqrt{8^{2}+(-7)^{2}+(-2)^{2}} sqrt{7^{2}+(-11)^{2}+8^{2}}} &=\=frac{56+77-16}{sqrt{64+49+4} sqrt{49+121+64}}=frac{117}{sqrt{117} sqrt{234}}=\=frac{117}{117 sqrt{2}}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} end{aligned}$$

Угол же будет равен

$$phi=arccos left(frac{sqrt{2}}{2}right)=45^{circ}$$

Ответ. $phi=45^{circ}$

Читать дальше: как найти косинус угла между векторами.

Источник

Нахождение угла между векторами с помощью скалярного произведения

Пример 1

Пример 2

Пример 3

Пример 4

Нахождение угла между векторами с помощью векторного произведения

Пример 1

Пример 2

Тест по теме “Как найти угол между двумя векторами”

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Примеры вычисления угла между векторами для пространственных задач

Скалярное произведение векторов

Справочник по высшей математике

Оглавление

python — Как узнать угол между двумя векторами?

Калькулятор угла между двумя векторами

Вектор в математике

Что такое угол между двумя векторами?

Как найти угол между двумя векторами

Формулы угла между двумя векторами

Калькулятор угла между двумя векторами — как пользоваться?

Угол между двумя векторами — пример

Формула

Примеры вычисления угла между векторами