Как найти угол между векторами по уравнению

Угол между векторами.

Формула вычисления угла между векторами

cos α =	a · b
| a |·| b |

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5

Найдем угол между векторами:

cos α =	a · b	=	24	=	24	= 0.96
| a | · | b |	5 · 5	25

Решение: Найдем скалярное произведение векторов:

a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α =	a · b	=	40	=	40	=	4	= 0.8
| a | · | b |	5√ 2 · 5√ 2	50	5

Примеры вычисления угла между векторами для пространственных задач

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6

Найдем угол между векторами:

cos α =	a · b	=	28	=	14
| a | · | b |	5 · 6	15

Решение: Найдем скалярное произведение векторов:

a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Нахождение угла между векторами

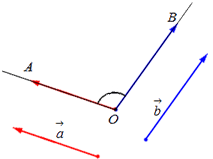
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

1. Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

1. Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Как найти угол между векторами

Вы будете перенаправлены на Автор24

Угол между векторами

Для того, чтобы мы могли ввести формулу для вычисления угла между векторами через координаты, нужно сначала разобраться с самим понятием угла между этими векторами.

Пусть нам даны два вектора $overline<α>$ и $overline<β>$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline<α>=overline$ и $overline<β>=overline$, тогда угол $AOB$ будет носить название угол между двумя векторами. (рис. 1).

Рисунок 1. Угол между векторами. Автор24 — интернет-биржа студенческих работ

Причем мы будем считать, что если векторы $overline<α>$ и $overline<β>$ будут сонаправленными, или один или оба из них будет нулевым вектором, то угол между этими векторами будет равняться $0^circ$.

Нахождение угла между векторами в пространстве с помощью скалярного произведения

Вспомним сначала, что называется скалярным произведением и каким образом его можно находить.

Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.

Скалярное произведение двух данных векторов $overline<δ>$ и $overline<β>$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, равняется сумме произведений их соответствующих координат.

Математически выглядит следующим образом

$overline<δ>cdot overline<β>=δ_1 δ_2+β_1 β_2+γ_1 γ_2$

Готовые работы на аналогичную тему

Обозначение: $overline<δ>cdot overline<β>$.

С помощью скалярного произведения мы можем найти косинус угла между векторами. Пусть нам даны векторы $overline<δ>$ и $overline<β>$ с координатами $(δ_1,β_1,γ_1)$ и $(δ_2,β_2,γ_2)$, соответственно. Из определения 2 получим, что

Из теоремы 1 мы знаем, что $overline<δ>cdot overline<β>=δ_1 δ_2+β_1 β_2+γ_1 γ_2$, следовательно

Расписывая по формуле длины вектора значения $|overline<δ>|$ и $|overline<β>|$, окончательно получим

Найдя значение косинуса, мы легко найдем и значение самого угла.

Найти косинус угла между векторами $overline<δ>$ и $overline<β>$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.

Решение.

Найдем скалярное произведение между данными векторами через координаты:

$overline<δ>cdot overline<β>=1cdot 3+(-2)cdot 0+2cdot 4=11$

Найдем длины этих векторов:

В результате, получим

Нахождение угла между векторами с помощью векторного произведения

Вспомним сначала, определение векторного произведения и каким образом его можно находить.

Векторным произведением двух векторов называется такой вектор, который будет перпендикулярен обоим данным векторам, и его длина равна произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют ту же ориентацию, как и декартова система координат.

Математически это выглядит следующим образом:

1. $|overline<δ>хoverline<β>|=|overline<δ>||overline<β>|sin⁡∠(overline<δ>,overline<β>)$
2. $overline<δ>хoverline<β>⊥overline<δ>$, $overline<δ>хoverline<β>⊥overline<β>$
3. $(overline<δ>хoverline<β>,overline<δ>,overline<β>)$ и $(overline,overline,overline)$ одинаково ориентированы (рис. 2)

Рисунок 2. Векторное произведение. Автор24 — интернет-биржа студенческих работ

Для нахождения вектора векторного произведения можно пользоваться следующей формулой:

С помощью векторного произведения мы можем найти синус угла между данными векторами. Пусть нам даны векторы $overline<δ>$ и $overline<β>$ с координатами $(δ_1,δ_2,δ_3)$ и $(β_1,β_2,β_3)$, соответственно. Из определения 3 получим, что

Найдем вектор векторного произведения по формуле:

$overline<δ>хoverline<β>=beginoverline&overline&overline\δ_1&δ_2&δ_3\β_1&β_2&β_3end=(δ_2 β_3-δ_3 β_2,δ_3 β_1-δ_1 β_3,δ_1 β_2-δ_2 β_1)$

Расписывая по формуле длины вектора значения $|overline<δ>|$, $|overline<β>|$ и $|overline<δ>хoverline<β>|$, окончательно получим

Найдя значение синуса, мы легко найдем и значение самого угла между векторами через координаты через формулу.

Найти синус угла между векторами $overline<δ>$ и $overline<β>$, имеющими координаты $(1,-2,2)$ и $(3,0,4)$, соответственно.

Решение.

Найдем вектор векторного произведения между данными векторами по формуле:

Найдем длины этих векторов:

В результате, получим

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 20 07 2021

источники:

http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/

http://spravochnick.ru/geometriya/metod_koordinat_v_prostranstve/kak_nayti_ugol_mezhdu_vektorami/

Угол между векторами

Иногда студенты при решении задач аналитической геометрии сталкиваются с вопросом: «Как найти угол между векторами?». Чтобы решить такую задачу нужно сначала найти косинус угла между ними, а затем и сам угол. Для этого применяется такая формула: $$ phi = arccos(cos phi) $$

Если воспользоваться данной формулой, то сначала нужно найти угол между векторами $ cos phi $. Затем находим арккосинус от косинуса угла $ phi $. А чему равен $ cos phi $? Для его нахождения необходимо воспользоваться следующими формулами.

Формула

Если векторы расположены на плоскости и координаты их заданы в виде: $ overline{a} = (a_x; a_y) $ и $ overline{b} = (b_x; b_y) $, то найти угол между ними можно так:

$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{a_xcdot b_x + a_y cdot b_y}{sqrt{a_x ^2 + a_y ^2}cdot sqrt{b_x ^2 + b_y ^2}} $$

Если вектора находятся в пространстве и координаты каждого из них заданы в виде: $ overline{a} = (a_x; a_y; a_z) $ и $ overline{b} = (b_x; b_y; b_z) $, то вычислить косинус угла следует по формуле:

$$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{a_xcdot b_x + a_y cdot b_y + a_z cdot b_z}{sqrt{a_x ^2 + a_y ^2 + a_z ^2}cdot sqrt{b_x ^2 + b_y ^2 + b_z ^2}} $$

Пояснение. В числителе расположено скалярное произведение векторов $ overline{a} $ и $ overline{b} $. Оно равно сумме произведений соответствующих координат. В знаменателе перемножаются модули (длины) векторов.

Примеры решений

Пример 1

Найти угол между векторами $ overline{a} = (2;4) $ и $ overline{b} = (3;1) $

Решение

Сначала находим косинус угла между векторами по формуле: $$ cos phi = frac{(overline{a},overline{b})}{|overline{a}| cdot |overline{b}|} = frac{2cdot 3 + 4 cdot 1}{sqrt{2^2 + 4^2} cdot sqrt{3^2 + 1^2} } = frac{10}{sqrt{20} cdot sqrt{10}} = $$ $$ = frac{10}{sqrt{200}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Теперь искомый угол $ phi $ находим по другой формуле: $$ phi = arccos (cos phi) = arccos (cos frac{sqrt{2}}{2}) = 45^0 $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

Угол между двумя векторами равен $ phi = 45^0 $

Пример 2

Найти угол $ phi $ между двумя векторами $ overline{a} = (8;-11;7) $ и $ overline{b} = (-2;-7;8) $

Решение

Подставляем координаты в формулу и вычисляем: $$ cos phi = frac{8cdot (-2) + (-11)cdot (-7) + 7cdot 8}{sqrt{8^2+(-11)^2+7^2} cdot sqrt{(-2)^2+(-7)^2+8^2} } = $$ $$ = frac{-16+77+56}{sqrt{234} cdot sqrt{117}} = frac{117}{sqrt{234} cdot sqrt{117}} = $$ $$ = frac{sqrt{117}}{sqrt{234}} = frac{1}{sqrt{2}} = frac{sqrt{2}}{2} $$ Далее находим сам угол $ phi $ с помощью арккосинуса: $$ phi = arccos frac{sqrt{2}}{2} = 45^0 $$

Ответ

Угол $ phi = 45^0 $

Нахождение угла между векторами с помощью скалярного произведения

Косинус угла между векторами a⃗=(a1;a2)vec{a}=(a_{1};a_{2}) и b⃗=(b1;b2)vec{b}=(b_{1};b_{2}) может быть вычислен по формуле

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=a1⋅b1+a2⋅b2a12+a22⋅b12+b22.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}= frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}}{sqrt{a_{1}^{2}+a_{2}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}}}.

Следовательно, угол между векторами a⃗=(a1;a2)vec{a}=(a_{1};a_{2}) и b⃗=(b1;b2)vec{b}=(b_{1};b_{2}) может быть вычислен по формуле

(a⃗,b⃗^)=arccos⁡(a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣)=arccos⁡(a1⋅b1+a2⋅b2a12+a22⋅b12+b22).left(widehat{vec{a},vec{b}}right)=arccosleft(frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}right)=arccosleft(frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}}{sqrt{a_{1}^{2}+a_{2}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}}}right).

Пример 1

Найти угол между векторами a⃗=(1;−1)vec{a}=(1; -1) и b⃗=(1;2).vec{b}=(1; 2).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=1⋅1+(−1)⋅212+(−1)2⋅12+22=1−22⋅5=−110.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{1cdot1+(-1)cdot2}{sqrt{1^{2}+(-1)^{2}}cdot sqrt{1^{2}+2^{2}}}=frac{1-2}{sqrt{2}cdotsqrt{5}}=frac{-1}{sqrt{10}}.

(a⃗,b⃗^)=arccos⁡(−110)=arccos⁡(−1010).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{-1}{sqrt{10}} right )=arccosleft ( frac{-sqrt{10}}{10} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(−1010).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{-sqrt{10}}{10} right).

Пример 2

Найти угол между векторами a⃗=(2;3)vec{a}=(2; 3) и b⃗=(3;1).vec{b}=(3; 1).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=2⋅3+3⋅122+32⋅32+12=6+313⋅10=9130=9130130.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{2cdot3+3cdot1}{sqrt{2^{2}+3^{2}}cdot sqrt{3^{2}+1^{2}}}=frac{6+3}{sqrt{13}cdotsqrt{10}}=frac{9}{sqrt{130}}=frac{9sqrt{130}}{130}.

(a⃗,b⃗^)=arccos⁡(9130130).left ( widehat{vec{a},vec{b}} right )=arccosleft ( frac{9sqrt{130}}{130} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(9130130).left ( widehat{vec{a},vec{b}} right )=arccos left ( frac{9sqrt{130}}{130} right ).

Косинус угла между векторами a⃗=(a1;a2;a3)vec{a}=(a_{1};a_{2};a_{3}) и b⃗=(b1;b2;b3)vec{b}=(b_{1};b_{2};b_{3}) может быть вычислен по формуле

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=a1⋅b1+a2⋅b2+a3⋅b3a12+a22+a32⋅b12+b22+b32.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}= frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}+a_{3}cdot b_{3}}{sqrt{a_{1}^{2}+a_{2}^{2}+a_{3}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}+b_{3}^{2}}}.

Следовательно, угол между векторами a⃗=(a1;a2;a3)vec{a}=(a_{1};a_{2};a_{3}) и b⃗=(b1;b2;b3)vec{b}=(b_{1};b_{2};b_{3}) может быть вычислен по формуле

(a⃗,b⃗^)=arccos⁡(a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣)=arccos⁡(a1⋅b1+a2⋅b2+a3⋅b3a12+a22+a32⋅b12+b22+b32).left(widehat{vec{a},vec{b}}right)=arccosleft(frac{vec{a}cdotvec{b}}{|vec{a}|cdot|vec{b}|}right)=arccosleft(frac{a_{1}cdot b_{1}+a_{2}cdot b_{2}+a_{3}cdot b_{3}}{sqrt{a_{1}^{2}+a_{2}^{2}+ a_{3}^{2}}cdotsqrt{b_{1}^{2}+b_{2}^{2}+ b_{3}^{2}}}right).

Пример 3

Найти угол между векторами a⃗=(1;2;3)иb⃗=(1;−2;3).vec{a}=(1; 2; 3) и vec{b}=(1; -2; 3).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=1⋅1+2⋅(−2)+3⋅312+22+32⋅12+(−2)2+32=1−4+914⋅14=614=37.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{1cdot1+2cdot(-2)+3cdot3}{sqrt{1^{2}+2^{2}+3^{2}}cdot sqrt{1^{2}+(-2)^{2}+3^{2}}}=frac{1-4+9}{sqrt{14}cdotsqrt{14}}=frac{6}{14}=frac{3}{7}.

(a⃗,b⃗^)=arccos⁡(37).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{3}{7} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(37).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{3}{7} right ).

Пример 4

Найти угол между векторами a⃗=(2;−1;−2)vec{a}=(2; -1; -2) и b⃗=(1;3;−2).vec{b}=(1; 3; -2).

cos⁡(a⃗,b⃗^)=a⃗⋅b⃗∣a⃗∣⋅∣b⃗∣=2⋅1+(−1)⋅3+(−2)⋅(−2)22+(−1)2+(−2)2⋅12+32+(−2)2=2−3+49⋅14=33⋅14=114=1414.cosleft(widehat{vec{a},vec{b}}right)=frac{vec{a}cdot vec{b}}{left | vec{a} right |cdot left | vec{b} right |}=frac{2cdot1+(-1)cdot3+(-2)cdot(-2)}{sqrt{2^{2}+(-1)^{2}+(-2)^{2}}cdot sqrt{1^{2}+3^{2}+(-2)^{2}}}=frac{2-3+4}{sqrt{9}cdotsqrt{14}}=frac{3}{3cdotsqrt{14}}=frac{1}{sqrt{14}}=frac{sqrt{14}}{14}.

(a⃗,b⃗^)=arccos⁡(1414).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{sqrt{14}}{14} right ).

Ответ: (a⃗,b⃗^)=arccos⁡(1414).left(widehat{vec{a},vec{b}}right)=arccosleft ( frac{sqrt{14}}{14} right ).

Нахождение угла между векторами с помощью векторного произведения

Синус угла между векторами можно вычислить по формуле: sin⁡(a⃗,b⃗^)=∣a⃗×b⃗∣∣a⃗∣⋅∣b⃗∣.sin(widehat{vec{a},vec{b}})=frac{left | vec{a}times vec{b} right |}{left | vec{a} right |cdotleft | vec{b} right |}.

Пример 1

Найти угол между векторами a⃗=(2;−1;2)vec{a}=(2;-1;2) и b⃗=(3;0;1).vec{b}=(3;0;1).

a⃗×b⃗=∣ijk2−12301∣=(−1−0)i−(2−6)j+(0+3)k=−i+4j+3k.vec{a}times vec{b}=begin{vmatrix}i&j&k\2&-1&2\3&0&1end{vmatrix}=(-1-0)i-(2-6)j+(0+3)k=-i+4j+3k.

∣a⃗×b⃗∣=(−1)2+42+32=1+16+9=26.left | vec{a}times vec{b} right |=sqrt{(-1)^{2}+4^{2}+3^{2}}=sqrt{1+16+9}=sqrt{26}.

∣a⃗∣=22+(−1)2+22=4+1+4=9=3.left | vec{a} right |=sqrt{2^{2}+(-1)^{2}+2^{2}}=sqrt{4+1+4}=sqrt{9}=3.

∣b⃗∣=32+02+12=9+0+1=10.left | vec{b} right |=sqrt{3^{2}+0^{2}+1^{2}}=sqrt{9+0+1}=sqrt{10}.

sin⁡(a⃗,b⃗^)=26310=132325=1335=6515.sin(widehat{vec{a},vec{b}})=frac{sqrt{26}}{3sqrt{10}}=frac{sqrt{13}sqrt{2}}{3sqrt{2}sqrt{5}}=frac{sqrt{13}}{3sqrt{5}}=frac{sqrt{65}}{15}.

(a⃗,b⃗^)=arcsin⁡(6515).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{65}}{15} right ).

Ответ: (a⃗,b⃗^)=arcsin⁡(6515).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{65}}{15} right ).

Пример 2

Найти угол между векторами a⃗=(1;1;3)vec{a}=(1;1;3) и b⃗=(0;1;1).vec{b}=(0;1;1).

a⃗×b⃗=∣ijk113011∣=(1−3)i−(1−0)j+(1−0)k=−2i−j+k.vec{a}times vec{b}=begin{vmatrix}i&j&k\1&1&3\0&1&1end{vmatrix}=(1-3)i-(1-0)j+(1-0)k=-2i-j+k.

∣a⃗×b⃗∣=(−2)2+(−1)2+12=4+1+1=6.left | vec{a}times vec{b} right |=sqrt{(-2)^{2}+(-1)^{2}+1^{2}}=sqrt{4+1+1}=sqrt{6}.

∣a⃗∣=12+12+32=1+1+9=11.left | vec{a} right |=sqrt{1^{2}+1^{2}+3^{2}}=sqrt{1+1+9}=sqrt{11}.

∣b⃗∣=02+12+12=0+1+1=2.left | vec{b} right |=sqrt{0^{2}+1^{2}+1^{2}}=sqrt{0+1+1}=sqrt{2}.

sin⁡(a⃗,b⃗^)=6112=32112=311=3311.sin(widehat{vec{a},vec{b}})=frac{sqrt{6}}{sqrt{11}sqrt{2}}=frac{sqrt{3}sqrt{2}}{sqrt{11}sqrt{2}}=frac{sqrt{3}}{sqrt{11}}=frac{sqrt{33}}{11}.

(a⃗,b⃗^)=arcsin⁡(3311).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{33}}{11} right ).

Ответ: (a⃗,b⃗^)=arcsin⁡(3311).(widehat{vec{a},vec{b}})=arcsinleft ( frac{sqrt{33}}{11} right ).

Тест по теме “Как найти угол между двумя векторами”

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a→ и b→ , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы OA→=b→ и OB→=b→

Углом между векторами a→ и b→ называется угол между лучами ОА и ОВ.

Полученный угол будем обозначать следующим образом: a→,b→^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a→,b→^=0, когда векторы являются сонаправленными и a→,b→^=π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π2 радиан.

Если хотя бы один из векторов является нулевым, то угол a→,b→^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a→, b→=a→·b→·cosa→,b→^.

Если заданные векторы a→ и b→ ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cosa→,b→^=a→,b→a→·b→

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a→=(ax, ay), b→=(bx, by) выглядит так:

cosa→,b→^=ax·bx+ay·byax2+ay2·bx2+by2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a→=(ax, ay, az), b→=(bx, by, bz) будет иметь вид: cosa→,b→^=ax·bx+ay·by+az·bzax2+ay2+az2·bx2+by2+bz2

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы OA→=a→ и OB→=b→ , тогда, согласно теореме косинусов в треугольнике ОАВ, будет верным равенство:

AB2=OA2+OB2-2·OA·OB·cos(∠AOB) ,

что равносильно:

b→-a→2=a→+b→-2·a→·b→·cos(a→, b→)^

и отсюда выведем формулу косинуса угла:

cos(a→, b→)^=12·a→2+b→2-b→-a→2a→·b→

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

cos(a→, b→)^=a→, b→a→·b→

Содержание:

• Формула
• Примеры вычисления угла между векторами

Формула

Чтобы найти угол $phi$ между векторами нужно вначале найти
косинус угла, а затем от него найти арккосинус, то есть:

$$phi=arccos (cos phi)$$

Косинус угла между векторами равен
скалярному произведению этих векторов, деленному на произведение их
длин.
В случае если векторы заданны на плоскости и имеют координаты
$bar{a}=left(a_{x} ; a_{y}right)$, $bar{b}=left(b_{x} ; b_{y}right)$, то косинус между ними вычисляется по формуле:

В случае, если векторы заданы в пространстве, то есть
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и $bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$, то косинус угла между ними равен:

Примеры вычисления угла между векторами

Читать дальше: как найти косинус угла между векторами.