Как найти угол между высотами треугольника? Зависит ли величина угла от вида треугольника?
Утверждение.
Один из углов, образованный высотами треугольника, проведёнными из двух его вершин, равен углу при третьей вершине.
Другой угол равен сумме углов треугольника, из вершин которых проведены высоты.
Доказательство:
1 способ
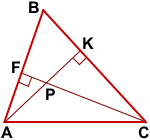
Рассмотрим остроугольный треугольник ABC.
Пусть AK и CF — его высоты.
Тогда ∠BFC=∠BKA=90°.
Так как сумма углов четырёхугольника равна 360°, то в 4-угольнике BKPF
∠BFP+∠FPK+∠BKP+∠FBK=360°,
откуда ∠FPK+∠FBK=180° и ∠FPK=180°-∠FBK.
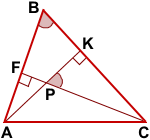
∠KPC=180°-∠FPK=180°-(180° -∠FBK)=∠FBK.
Так как сумма углов треугольника равна 180°,
∠BAC+∠FBK+∠ACB=180°,
∠FBK=180°-(∠BAC+∠ACB),
∠FPK=180°-∠FBK=180° -(180° -(∠BAC+∠ACB))=∠BAC+∠ACB.
2 способ
Прямоугольные треугольники BCF и PKC подобны по общему острому углу C. Следовательно, ∠KPC=∠FBC.
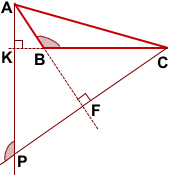
Если треугольник ABC — тупоугольный, рассуждения и вывод аналогичны.
Утверждение верно и для прямоугольного треугольника.
То есть для любого треугольника ABC один из углов между высотами, проведёнными из вершин A и C, равен углу B, другой — сумме углов A и C.
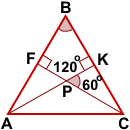
∠KPC=60°,
∠FPK=120°.
Угол между высотами треугольника
Как найти угол между высотами треугольника? Зависит ли величина угла от вида треугольника?
Один из углов, образованный высотами треугольника, проведёнными из двух его вершин, равен углу при третьей вершине.
Другой угол равен сумме углов треугольника, из вершин которых проведены высоты.
Рассмотрим остроугольный треугольник ABC.
Пусть AK и CF — его высоты.
Так как сумма углов четырёхугольника равна 360°, то в 4-угольнике BKPF
откуда ∠FPK+∠FBK=180° и ∠FPK=180°-∠FBK.
∠FPK+∠KPC=180° (как смежные).
∠FPK=180°-∠FBK=180° -(180° -(∠BAC+∠ACB))=∠BAC+∠ACB.
Прямоугольные треугольники BCF и PKC подобны по общему острому углу C. Следовательно, ∠KPC=∠FBC.
Если треугольник ABC — тупоугольный, рассуждения и вывод аналогичны.
Утверждение верно и для прямоугольного треугольника.
То есть для любого треугольника ABC один из углов между высотами, проведёнными из вершин A и C, равен углу B, другой — сумме углов A и C.
В частности, один угол между высотами равностороннего треугольника равен 60°, другой — 120°:
Найдите угол между высотами треугольника, проведенными из вершин его меньших внутренних углов?
Геометрия | 5 — 9 классы
Найдите угол между высотами треугольника, проведенными из вершин его меньших внутренних углов.
Если внешние углы этого треугольника пропорциональны числам 6, 7 и 11.
Сумма внешних углов равна 360 гр
Составим уравнение 6х + 7х + 11х = 360
Значит внешние углы соответственно равны 90 гр, 105 гр, 165 гр
Тогда углы внутренние у треугольника равны 90 гр, 75 гр, 15 гр соотвественно
Высоты прведены из острых углов, то есть из углов 75 и 15 гр.
Так как треугольник прямоугольный, то угол между высотами 90 гр.
Внешний угол треугольника при вершине В в три раза больше его внутреннего угла А и на 40(градусов)больше внутреннего угла С?
Внешний угол треугольника при вершине В в три раза больше его внутреннего угла А и на 40(градусов)больше внутреннего угла С.
Найдите углы треугольника.
Внутренние углы треугольника пропорциональны числам 2, 5, 8 а)найдите угла треугольника АBC б)найдите внешние углы треугольника ABC?
Внутренние углы треугольника пропорциональны числам 2, 5, 8 а)найдите угла треугольника АBC б)найдите внешние углы треугольника ABC.
В треугольнике ABC угол A меньше угла B в 3 раза, а внешний угол при вершине A больше внешнего угла при вершине B на 40 градусов?
В треугольнике ABC угол A меньше угла B в 3 раза, а внешний угол при вершине A больше внешнего угла при вершине B на 40 градусов.
Найдите внутренние углы треугольника ABC.
Внешний угол при основании равнобедренного треугольника на 40 градусов больше смежного с ним внутреннего угла треугольника?
Внешний угол при основании равнобедренного треугольника на 40 градусов больше смежного с ним внутреннего угла треугольника.
Найдите величину угла при вершине треугольника.
В прямоугольном треугольнике угол между высотой и медианой проведенным из вершины поимого угла равен 14градусах, найдите меньший из двух острых углов треугольника?
В прямоугольном треугольнике угол между высотой и медианой проведенным из вершины поимого угла равен 14градусах, найдите меньший из двух острых углов треугольника.
В треугольнике АВС угол А меньше угла В в три раза , а внешний угол при вершине А больше внешнего угла при вершине В на 40 градусов ?
В треугольнике АВС угол А меньше угла В в три раза , а внешний угол при вершине А больше внешнего угла при вершине В на 40 градусов .
Найдите внутренние углы треугольника АВС ?
Один из внутренних углов треугольника на 18 градусов меньше от другого, а внешний угол при вершине третьего угла равняется 126 градусов?
Один из внутренних углов треугольника на 18 градусов меньше от другого, а внешний угол при вершине третьего угла равняется 126 градусов.
Найдите углы треугольника.
Один из внешних углов треугольника в два раза больше другого внешнего угла этого треугольника?
Один из внешних углов треугольника в два раза больше другого внешнего угла этого треугольника.
Найдите меньший из них, если внутренний угол треугольника, не смежный с указанными внешними углами, равен 60 гр.
Один из внутренних углов треугольника на 14° больше другого, а внешний угол при вершине 3 — го угла равен110°?
Один из внутренних углов треугольника на 14° больше другого, а внешний угол при вершине 3 — го угла равен110°.
Найдите углы треугольника.
Помогите пожалуйста внешний угол треугольника при вершине B в 3 раза больше его внутреннего угла А и на 40 градусов больше внутреннего угла С найдите углы треугольника?
Помогите пожалуйста внешний угол треугольника при вершине B в 3 раза больше его внутреннего угла А и на 40 градусов больше внутреннего угла С найдите углы треугольника.
Вы находитесь на странице вопроса Найдите угол между высотами треугольника, проведенными из вершин его меньших внутренних углов? из категории Геометрия. Уровень сложности вопроса рассчитан на учащихся 5 — 9 классов. На странице можно узнать правильный ответ, сверить его со своим вариантом и обсудить возможные версии с другими пользователями сайта посредством обратной связи. Если ответ вызывает сомнения или покажется вам неполным, для проверки найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте новый вопрос, используя ключевые слова: введите вопрос в поисковую строку, нажав кнопку в верхней части страницы.
Одно из свойствы треугольника : Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон : a Существует ли четырех угольник зл сторонами 2см 6 см 9см 17см?
Треугольник. Числовые зависимости между элементами треугольника (сторон, высот, медиан).
Теорема.
Если стороны прямоугольного треугольника измерены одной единицей, то квадрат числа, выражающего гипотенузу равен сумме квадратов чисел, выражающих катеты.
Эту теорему обыкновенно выражают сокращенно так:
Квадрат гипотенузы равен сумме квадратов катетов.
Это соотношение было впервые замечено греческим геометром Пифагором (VI в. до н.э.) и носит поэтому его имя — теорема Пифагора.
В треугольнике квадрат стороны, лежащей против острого угла, равен сумме квадратов двух других сторон без удвоенного произведения какой-нибудь из этих сторон на ее отрезок от вершины острого угла до высоты.
Пусть BС — сторона треугольника ABС (черт. 1 и черт. 2), лежащая против острого угла A , и BD — высота опущенная на какую-либо из остальных сторон, например, на AС (или на ее продолжение).Требуется доказать, что:
Из прямоугольных треугольников BDС и ABD выводим:
Подставив в равенство [1] вместо BD 2 и DС 2 их выражения из равенств [2] и [3] , получим:
Это равенство, после сокращения членов -AD 2 и +AD 2 , и есть то самое, которое требовалось доказать.
Замечание. Доказанная теорема остается верной и тогда, когда угол С прямой. Тогда отрезок СD обратится в ноль, т.е. AС станет равна AD, и мы будем иметь:
Что согласуется с теоремой о квадрате гипотенузы.
Теорема.
В треугольнике квадрат стороны, лежащей против тупого угла, равен сумме квадратов двух других сторон, сложенных с удвоенным произведением какой-нибудь из этих сторон на отрезок ее продолжения от вершины тупого угла до высоты. Доказательство аналогично предыдущему.
Следствие.
Из трех последних теорем выводим, что квадрат стороны треугольника равен, меньше или больше суммы квадратов других сторон, смотря по тому, будет ли противолежащий угол прямой, острый или тупой.
Отсюда следует обратное предложение: Угол треугольника окажется прямым, острым или тупым, смотря по тому, будет ли квадрат противолежащей стороны равен, меньше или больше суммы квадратов других сторон.
Вычисление высоты треугольника по его сторонам.
Обозначим высоту, опущенную на сторону а треугольника ABС , через ha. Чтобы вычислить ее, предварительно из уравнения:
находим отрезок основания с’:
.
После чего из DABD определяем высоту, как катет:
.
Таким же путем можно определить высоты hb и hс , опущенные на стороны b и с.
Вычисление медиан треугольника по его сторонам.
Пусть даны стороны треугольника ABС и требуется вычислить его медиану BD. Для этого продолжим ее на расстояние DE = BD и точку E соединим с A и С. Тогда получим параллелограмм ABCE.
Тогда .
http://geometria.my-dict.ru/q/1127275_najdite-ugol-mezdu-vysotami-treugolnika-provedennymi/
http://www.calc.ru/Chislovyye-Zavisimosti-Mezhdu-Elementami-Treugolnika-Storon-.html
Высота треугольника — подробнее
Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).
На этом рисунке ( displaystyle BH) – высота.
Но иногда высота (в отличие от биссектрисы и медианы) ведёт себя, как непослушный ребенок – «выбегает» из треугольника. Это бывает в тупоугольном треугольнике.
И тогда получается так:
В общем, не нужно пугаться, если основание высоты оказалось не на стороне треугольника, а «за» треугольником, на продолжении стороны.
Как же решать задачи, в которых участвует высота?
Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.
Но попадаются задачи и похитрее, при решении которых лучше обладать дополнительными знаниями заранее, а не выводить их «с нуля». Сейчас мы обсудим некоторые из них.
Но для начала решим простенькую задачку на высоту в тупоугольном треугольнике:
В треугольнике ( displaystyle ABC) с тупым углом ( displaystyle C) проведена высота ( displaystyle BH). Найти ( displaystyle AC), если ( AB=2sqrt{10}), ( BC=sqrt{13}), ( BH=2).
Смотри: из-за того, что угол ( C) – тупой, высота ( BH) опустилась на продолжение стороны ( AC), а не на саму сторону.
Теперь давай увидим во всём этом два прямоугольных треугольника.
Смотри их целых два:
Применяем теорему Пифагора к треугольнику ( BCH):
( B{{C}^{2}}=B{{H}^{2}}+C{{H}^{2}}), то есть ( 13=4+C{{H}^{2}}); ( CH=3).
А теперь теорема Пифагора для ( Delta ABH):
( A{{B}^{2}}=A{{H}^{2}}+B{{H}^{2}}); то есть ( 40=A{{H}^{2}}+4); ( AH=6).
Теперь осталось только заметить, что ( AC=AH-CH=6-3=3).
Нашли!
А теперь давай вернемся к нашим высотам!
Остроугольный треугольник и высота
Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:
Что видим теперь? Ещё подобные треугольники!
Как от двух линий вообще могут получиться столько подобных треугольников?!
Но тем не менее…
( Delta C{{H}_{C}}Bsim Delta C{{H}_{A}}Hsim Delta A{{H}_{A}}Bsim Delta A{{H}_{C}}H)
Видишь, какое богатство? И всё это может быть использовано в задачах!
Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.
Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…
Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.
И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!
Элементы треугольника. Высоты, медианы, биссектрисы
Высоты, медианы и биссектрисы треугольника постоянно встречаются нам в задачах по геометрии. Мы начнем с таблицы, в которой показано, что такое высоты, медианы и биссектрисы, и какими свойствами они обладают. Затем — подробные объяснения и решение задач.
Высотой треугольника называется перпендикуляр,
опущенный из вершины треугольника
на противоположную сторону.
В тупоугольном треугольнике высота
опускается на продолжение стороны.
Три высоты треугольника всегда
пересекаются в одной точке.
В случае тупого угла пересекаются
продолжения высот.
Медианой треугольника называют отрезок,
соединяющий вершину треугольника с
серединой противоположной стороны.
Три медианы треугольника пересекаются в
одной точке и делятся в ней в отношении
2 : 1 , считая от вершины.
Биссектриса треугольника делит
угол треугольника пополам.
Три биссектрисы пересекаются в одной точке,
которая является центром окружности,
вписанной в треугольник.
Напомним, что высота треугольника — это перпендикуляр, опущенный из его вершины на противоположную сторону.
Три высоты треугольника всегда пересекаются в одной точке. Вот как это выглядит в случае остроугольного треугольника.
Попробуйте провести три высоты в тупоугольном треугольнике. Получилось? Да, редкий выпускник справляется с этим заданием. Действительно, мы не можем опустить перпендикуляр из точки A на отрезок BC, зато можем опустить его на прямую BC — то есть на продолжение стороны BC.
В этом случае в одной точке пересекаются не сами высоты, а их продолжения.
В прямоугольном треугольнике каждый катет является высотой к другому катету. Три высоты прямоугольного треугольника пересекаются в вершине прямого угла.
Как доказать, что три высоты треугольника пересекаются в одной точке?
Доказательство здесь: Свойство высот треугольника.
Медиана треугольника — отрезок, соединяющий его вершину с серединой противоположной стороны.
Три медианы треугольника пересекаются в одной точке и делятся в ней в отношении 2 : 1, считая от вершины.
Доказательство этой теоремы смотрите здесь: Свойства медиан треугольника.
Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.
У биссектрисы угла есть замечательное свойство — точки, принадлежащие ей, равноудалены от сторон угла. Поэтому три биссектрисы треугольника пересекаются в одной точке, равноудаленной от всех сторон треугольника. Эта точка является центром окружности, вписанной в треугольник.
Читайте доказательство теоремы о том, что три биссектрисы треугольника пересекаются в одной точке:
Свойства биссектрис треугольника.
Еще одно свойство биссектрисы часто применяется при решении задач.
Теорема. Биссектриса треугольника делит противоположную сторону в отношении длин прилежащих сторон:
Доказательство этой теоремы здесь: Свойство биссектрисы треугольника.
Разберем несколько задач, в которых речь идет о высотах, медианах и биссектрисах треугольника. Все задачи взяты из Банка заданий ФИПИ.
Задача 1. Найдите острый угол между биссектрисами острых углов прямоугольного треугольника.
Ответ дайте в градусах.
Решение:
Пусть биссектрисы треугольник ABC (в котором угол C равен ) пересекаются в точке M.
Рассмотрим треугольник ABM.
,
, тогда
.
Острый угол между биссектрисами на рисунке обозначен .
Угол смежный с углом
, следовательно,
.
Поскольку треугольник — прямоугольный, то
.
Тогда .
Ответ: 45.
Задача 2. Острые углы прямоугольного треугольника равны и
. Найдите угол между высотой и биссектрисой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Пусть CH — высота, проведенная из вершины прямого угла C, CK — биссектриса угла C.
Тогда ;
.
Угол между высотой и биссектрисой — это угол .
.
Ответ: 16.
Задача 3. Острые углы прямоугольного треугольника равны и
. Найдите угол между высотой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Рассмотрим треугольник АВС, в котором угол С – прямой, CD – высота, СМ – медиана.
Требуется найти угол МСD.
Треугольник CMB – равнобедренный, т.к. медиана СМ равна половине гипотенузы АВ.
Следовательно,
Искомый
Ответ: 42.
Задача 4. Острые углы прямоугольного треугольника равны и
. Найдите угол между биссектрисой и медианой, проведенными из вершины прямого угла. Ответ дайте в градусах.
Решение:
Рассмотрим треугольник АВС, в котором угол С – прямой, CL – биссектриса, СМ – медиана.
. Требуется найти угол МСL.
Треугольник CMB – равнобедренный, т.к. медиана СМ равна половине гипотенузы АВ.
Следовательно,
т.к. CL – биссектриса.
Искомый
Ответ: 22.
Задача 5. Два угла треугольника равны и
. Найдите тупой угол, который образуют высоты треугольника, выходящие из вершин этих углов. Ответ дайте в градусах.
Решение:
Из треугольника ACH (угол H — прямой) найдем угол CAH. Он равен .
Из треугольника ACK ( K — прямой) найдем угол ACK. Он равен .
В треугольнике AOC известны два угла. Найдем третий, то есть угол AOC, который и является тупым углом между высотами треугольника ABC:
.
Ответ: 130.
Задача 6. В треугольнике ABC угол С равен , AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Решение:
Пусть в треугольнике ABC угол BAC равен A, угол ABC равен B.
Рассмотрим треугольник AOB.
,
, тогда
.
Из треугольника ABC получим, что .
Тогда .
Ответ: 119.
Задача 7. В треугольнике ABC угол A равен , угол B равен
. AD, BD и CF — биссектрисы, пересекающиеся в точке O. Найдите угол AOF. Ответ дайте в градусах.
Решение:
Найдем угол ACB. Он равен
Тогда
Из треугольника ACF найдем угол . Он равен
.
Рассмотрим треугольник AOF.
,
. Значит
.
Ответ: 49.
Задача 8. В треугольнике ABC, CD — медиана, угол ACB равен , угол B равен
. Найдите угол ACD. Ответ дайте в градусах.
Решение:
В прямоугольном треугольнике медиана равна половине гипотенузы.
Поэтому
Треугольник ADC равнобедренный, следовательно, углы при основании равны:
Поскольку в прямоугольном треугольнике сумма острых углов равна 90 градусов, получим:
Ответ: 32.
Задача 9. В треугольнике АВС АD — биссектриса, угол С равен . Угол САD равен
. Найдите угол В. Ответ дайте в градусах.
Решение:
Поскольку AD – биссектриса, то
Сумма углов треугольника равна , следовательно,
Ответ: 74.
Задача 10. В треугольнике АВС CH – высота, AD – биссектриса, О – точка пересечения прямых CH и AD, угол BAD равен . Найдите угол АОС. Ответ дайте в градусах.
Решение:
Угол АОС – внешний в треугольнике АНО, следовательно,
Ответ: 116.
Задача 11. В треугольнике АВС проведена биссектриса AD и AB = AD = CD. Найдите меньший угол треугольника АВС. Ответ дайте в градусах.
Решение:
AD = CD, следовательно, треугольник ADC – равнобедренный и
AD — биссектриса, следовательно,
AB = AD, следовательно, треугольник ABD – равнобедренный и
– внешний в треугольнике ADC, следовательно,
Таким образом, наименьшим углом треугольника АВС является , два других угла – в два раза больше.
Воспользуемся тем, что сумма углов треугольника АВС равна :
, откуда получаем:
Наименьший угол треугольника АВС равен .
Ответ: 36.
Задача 12. Биссектриса треугольника делит противоположную сторону на отрезки 2,8 и 4,2. Периметр треугольника равен 22. Найдите стороны треугольника.
Решение:
Пусть стороны треугольника равны и
. Биссектриса делит сторону c на отрезки 2,8 и 4,2.
Значит,
В соответствии со свойством биссектрисы:
Или:
Одновременно выполнено условие для периметра:
Тогда
Ответ: 9, 6, 7.
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Элементы треугольника. Высоты, медианы, биссектрисы» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Задача 11797 В равностороннем треугольнике АВС…
Условие
В равностороннем треугольнике АВС найдите величину острого угла между его высотами.
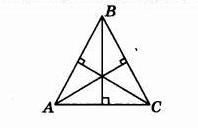
математика 8-9 класс
20200
Решение
Тогда угол между высотами будет равен 90 — 60 :2 = 90 — 30 = 60 (градусов).
Ответ: 60
Все решения

Точка пересечения высот треугольника является вершиной шести равных углов, сумма которых равна 360*. Отсюда искомый угол равен 360*:6=60*
Ответ: 60*