По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде?
Найдите правильный ответ на вопрос ✅ «По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде? …» по предмету 📘 Геометрия, а если вы сомневаетесь в правильности ответов или ответ отсутствует, то попробуйте воспользоваться умным поиском на сайте и найти ответы на похожие вопросы.
Смотреть другие ответы
Дано треугольник OBS угол B=90 градусов угол S=45 градусов OB=1008 СМ Найти SB
Ответы (1)
Дано abcd-параллелограмм, BCA=31 градусов, BAC=25 градусов
Ответы (1)
Один угол параллелограмма в 4 разОдин угол параллелограмма в 4 раза больше другого. Найдите больший угол. Ответ дайте в градусах. а больше другого. Найдите больший угол.
Ответы (1)
NK на 19 см. больше MN, MK = 81 см. Найти : MK, NK
Ответы (1)
Начертите угол AOB и лучи ОК и ОМ, проходящие между сторонами этого угла, так, чтобы угол AOB = 90, AOK = 40, MOB = 30, Найдите KOM
Ответы (1)
Главная » Геометрия » По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде?
поделиться знаниями или
запомнить страничку
- Все категории
-
экономические
43,663 -
гуманитарные
33,654 -
юридические
17,917 -
школьный раздел
611,987 -
разное
16,906
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде?
Вы открыли страницу вопроса По какой формуле найти угол наклона диагонали к плоскости основания в прямоугольном параллипипеде?. Он относится к категории
Геометрия. Уровень сложности вопроса – для учащихся 10 — 11 классов.
Удобный и простой интерфейс сайта поможет найти максимально исчерпывающие
ответы по интересующей теме. Чтобы получить наиболее развернутый ответ,
можно просмотреть другие, похожие вопросы в категории Геометрия,
воспользовавшись поисковой системой, или ознакомиться с ответами других
пользователей. Для расширения границ поиска создайте новый вопрос, используя
ключевые слова. Введите его в строку, нажав кнопку вверху.
Ответ: 10√2, 45°
Объяснение:
a = 6, b = 8, c = 10.
Диагональ прямоугольного параллелепипеда находится по формуле:
d = √(6² + 8² + 10²) = √(36 + 64 + 100) = √200 = 10√2
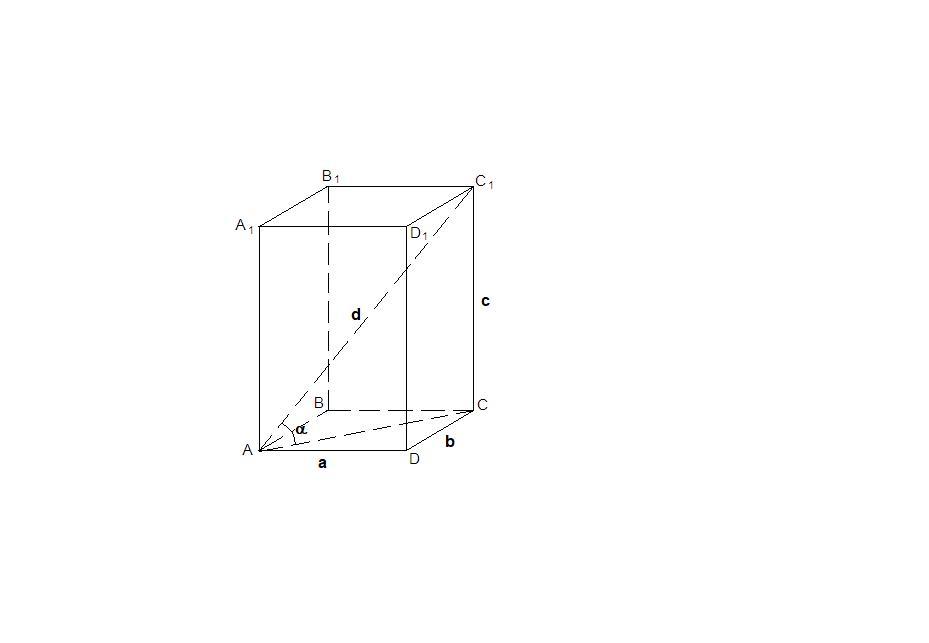
AC — проекция диагонали АС₁ на плоскость основания, значит ∠С₁АС — угол наклона диагонали к плоскости основания.
ΔС₁АС: ∠С₁СА = 90°,
sinα = c / d = 10 / (10√2) = 1/√2 = √2/2, ⇒
α = 45°
Приложения:
Советы к решению задач на призму
1. Если в условии задачи говорится диагональ боковой грани прямой призмы, то помните, что:
— Проекцией этой диагонали на плоскость основания будет соответствующая сторона основы призмы. Диагональ боковой грани прямой призмы, соответствующая ей сторона основания и боковое ребро призмы выходит с конца диагонали, образуют прямоугольный треугольник;
— Углом наклона диагонали боковой грани к плоскости основания будет угол между этой диагональю и соответствующей стороной основы призмы;
Если заданы или найдены диагональ боковой грани призмы и угол ее наклона к плоскости основания, или это диагональ и соответствующая ей сторона основы, то можно найти высоту призмы с помощью тригонометрических соотношений в прямоугольном треугольнике или последствий теоремы Пифагора.
2. Если в условии задачи говорится диагональ прямой призмы, то помните, что:
— Проекцией этой диагонали на плоскость основы будет соответствующая ей диагональ основания призмы. При этом большей диагонали основы соответствует большая диагональ призмы, меньшей — меньше диагональ призмы. Диагональ прямой призмы, соответствующая ей диагональ основания и боковое ребро призмы выходит с конца диагонали, образуют прямоугольный треугольник;
— Углом наклона диагонали прямой призмы к плоскости основания будет угол между этой диагональю и соответствующей диагональю основания призмы;
Если заданы или найдены диагональ прямой призмы и угол ее наклона к плоскости основания, или это диагональ и соответствующая ей диагональ основания основы, то можно найти высоту призмы с помощью тригонометрических соотношений в прямоугольном треугольнике или последствий теоремы Пифагора.
3. Если в условии задачи говорится сечение прямой призмы плоскостью, то помните, что:
— Если секущая плоскость проходит, например, через сторону основания прямой треугольной призмы и противоположную ей вершину призмы, принадлежащего другой основе, то сечением будет треугольник, ортогональной проекцией которого на плоскость основы будет треугольник, лежащий в основе призмы. Если известна площадь такого сечения и угол наклона плоскости сечения к плоскости основания, то можно найти площадь основания призмы. Площадь основания в таком случае будет равна площади сечения, помноженной на косинус угла между плоскостями сечения и основания. Соответственно площадь такого сечения будет равна площади основания, деленной на косинус угла между плоскостями сечения и основания.
Чтобы найти угол между плоскостью сечения и плоскостью основания, надо в одной из этих плоскостей провести перпендикуляр к общей прямой плоскостей и из основания перпендикуляра, во второй плоскости провести перпендикуляр к общей прямой плоскостей.
В случае правильной треугольной призмы угол наклона плоскости сечения, проходящей через сторону основания прямой треугольной призмы и противоположную ей вершину призмы к плоскости основания, будет угол между соответствующими высотами сечения и основы призмы.
