Как найти угол наклона плоскости формула

Правильный ответ такой: все эти случаи можно озаглавить геометрическим понятием «пересечение плоскости прямой под некоторым углом». Об этом мы сегодня и поговорим, а именно:

• рассмотрим главные определения и примеры;

• изучим свойства и теоремы по теме;

• научимся находить угол между прямой и плоскостью.

Определение угла между прямой и плоскостью

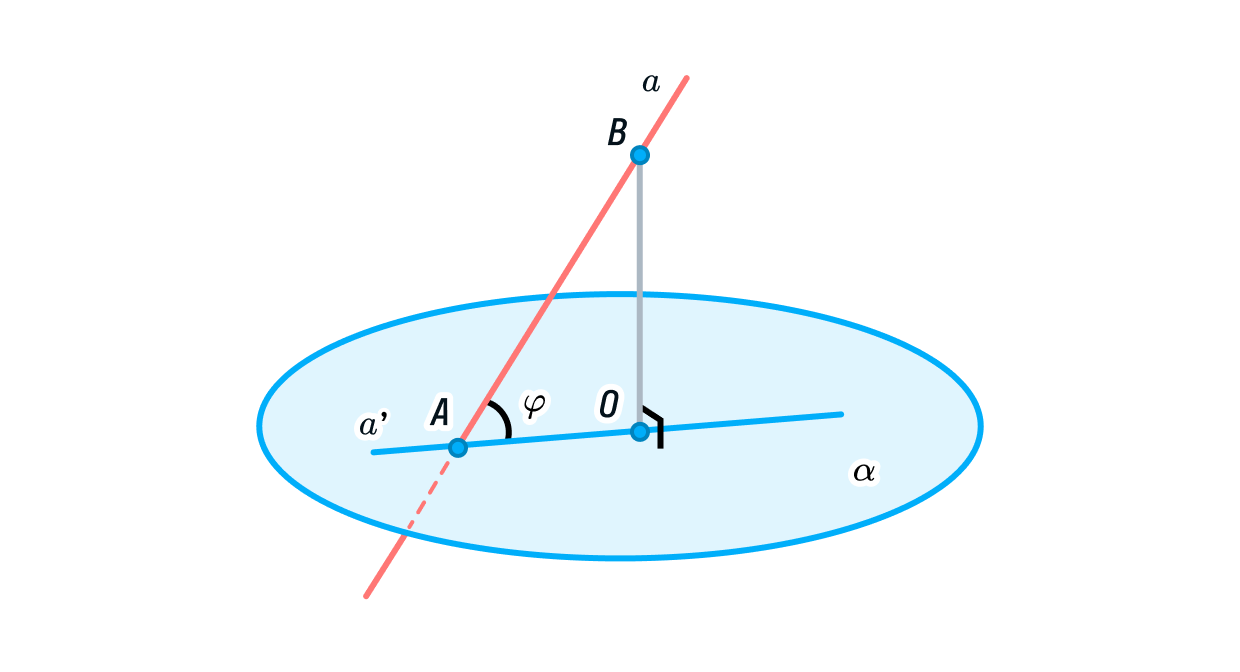
Угол между прямой и плоскостью — это угол между прямой и её проекцией на эту плоскость.

Мы уже знакомы с понятиями «угол», «прямая» и «плоскость» (если подзабыли, то можете повторить по нашим материалам). А сейчас давайте вспомним, что такое проекция.

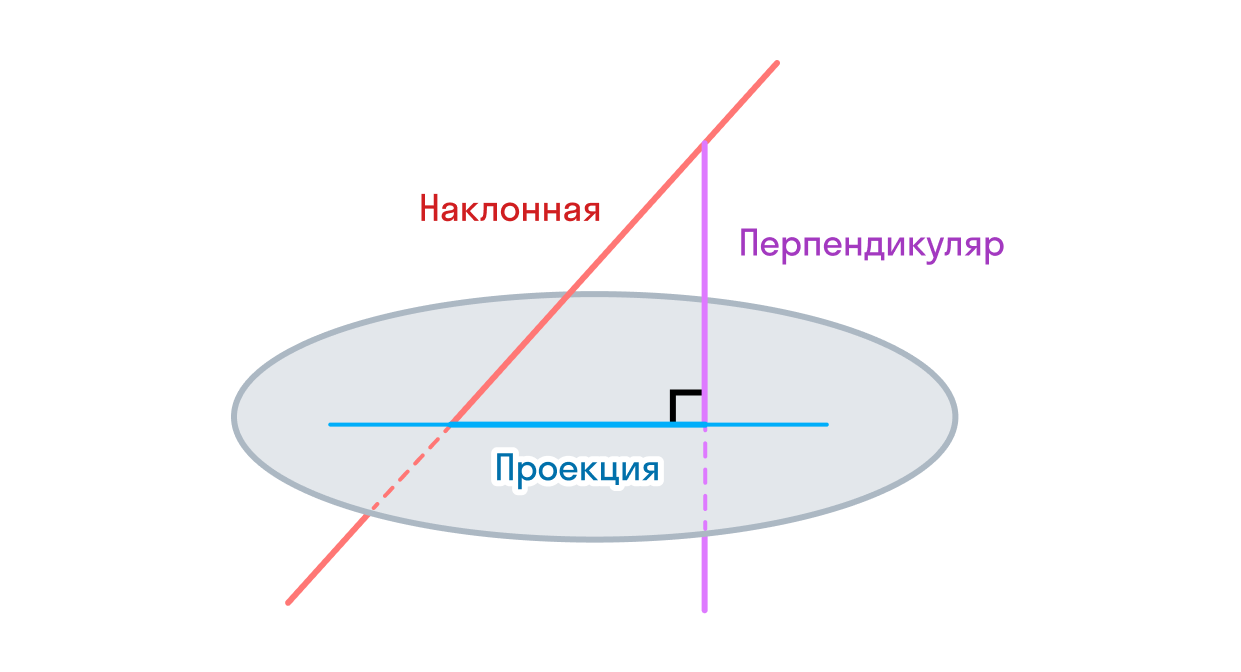
Проекция — это геометрическое изображение на плоскости, полученное проведением перпендикуляров из всех точек данного тела на плоскость.

То есть под углом между прямой и плоскостью в пространстве мы подразумеваем угол между прямой и её отображением на плоскость.

Также стоит заметить, что если прямая параллельна плоскости, то у них нет ни одной общей прямой, а значит, угол между ними не определяется.

Как вы думаете, какой тип имеет угол между прямой и плоскостью? Верно, он может быть только острым. Попробуйте доказать это самостоятельно 😊

Свойства и теоремы

Свойство угла между прямой и плоскостью

Углом между прямой и плоскостью называется наименьший из углов между прямой и произвольной прямой в плоскости.

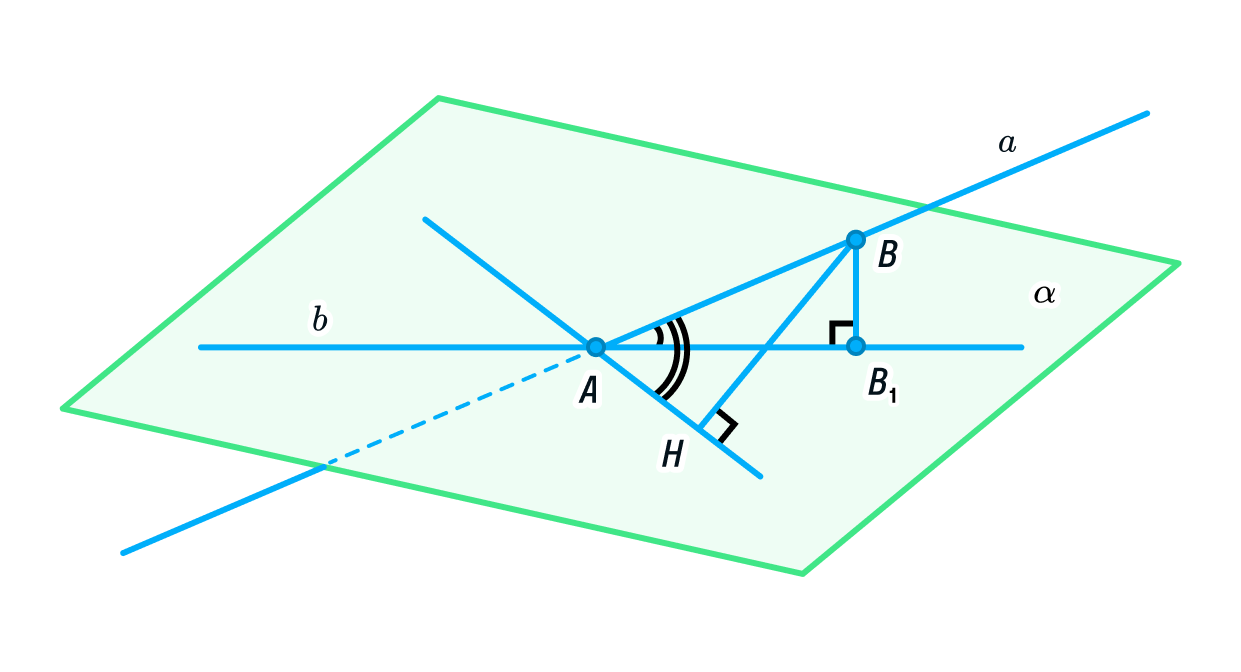
Попробуем привести доказательство. Для этого нарисуем плоскость и проведём к ней прямую АВ, являющуюся наклонной. Тогда АВ₁ — проекция прямой на плоскость, АН — произвольная прямая, принадлежащая плоскости, а ВН и ВВ₁ — перпендикуляры к плоскости (ВН ⟂ АН, ВВ₁ ⟂ АВ). Чтобы лучше представить себе этот объёмный чертеж, можно сделать небольшой макет из сложенного листа бумаги, прислонив его к поверхности стола или тетради.

Чтобы проверить истинность свойства, нам необходимо доказать, что угол ∠ВАВ₁ намного меньше, чем угол ∠ВАН.

Обозначим проблему: значения этих углов, как и других исходных, нам неизвестны. А значит, на помощь может прийти тригонометрия, ведь сравнить углы можно и через их синусы.

Синус — это отношение противолежащего угла к гипотенузе. В таком случае,

.

Оба перпендикуляра ВВ₁ и ВН проведены из точки В, но только один из них является кратчайшим расстоянием от точки по плоскости, и это перпендикуляр ВВ1. Так как значения синусов представляют собой дроби с одинаковыми знаменателями, большей будет та, у которой больше знаменатель.

Следовательно, sin ∠BAB1 < sin ∠BAH, ∠BAB1 < ∠BAH.

Теорема

Из двух наклонных, проведённых из одной точки к плоскости, меньшая образует с плоскостью больший угол, и наоборот: угол, образованный большей наклонной, будет меньшим из двух.

Существует множество разных доказательств этой теоремы, но мы сосредоточимся на одном из них.

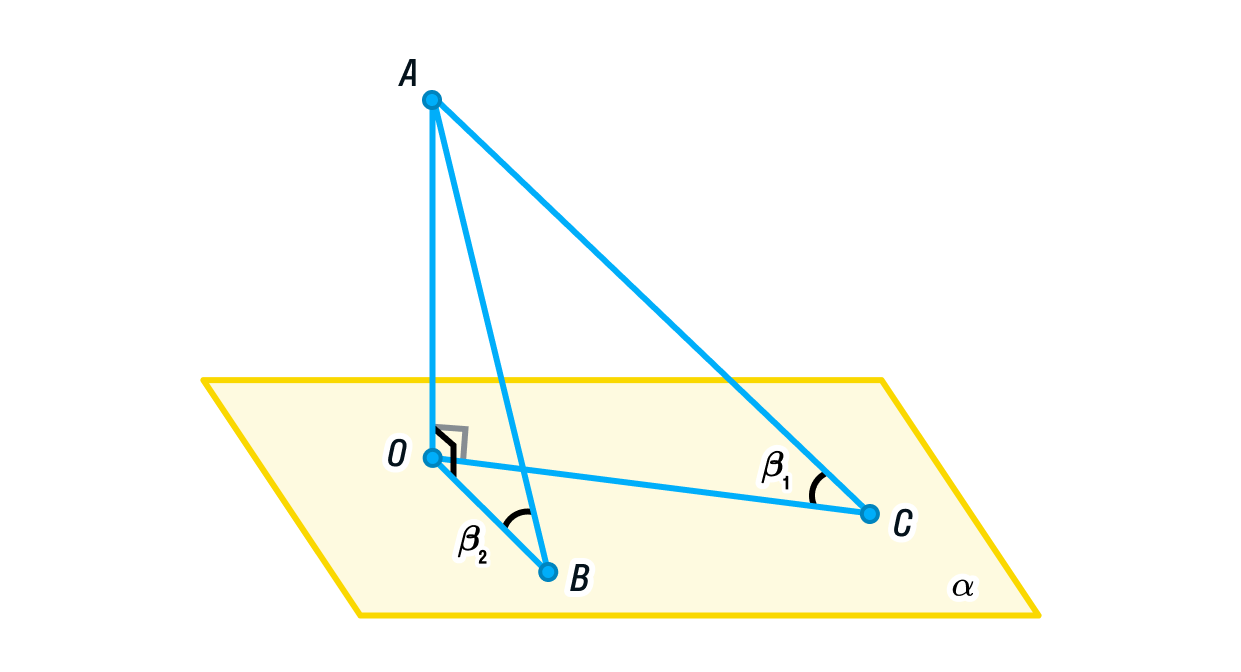
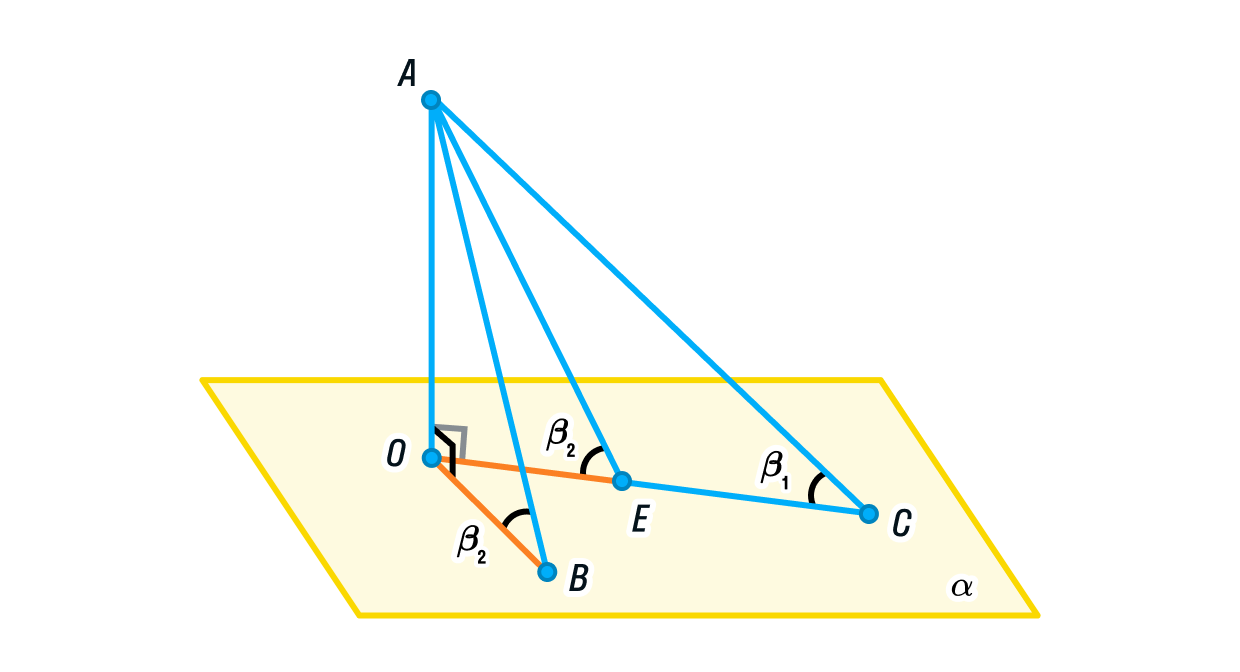
Для этого изобразим плоскость и точку

. Из точки А проведём две наклонные прямые, причем АВ < АС, а также перпендикуляр к плоскости АО.
Докажем, что ∠АВО > ∠АСО.

Стороны ОВ и ОС являются проекциями АВ и АС соответственно. Меньшая прямая имеет меньшую проекцию, а значит, ОВ < ОС.

Отложим на стороне ОС отрезок ОЕ, равный ОВ. Можно ли доказать равенство треугольников АОВ и АОЕ?

В данных треугольниках:

• ОВ = ОЕ (по построению),

• АО — общий катет.

Следовательно, треугольники АОВ и АОЕ равны по двум катетам (или по первому признаку: две стороны и угол между ними). В таком случае равны и соответственные углы: ∠АВО = ∠АЕО.

Угол АЕО является внешним для треугольника АЕС, и по свойству внешнего угла ∠АЕО = ∠АСЕ + ∠САЕ. Не трудно догадаться: раз угол АЕО равен сумме двух других углов треугольника, не смежных с ним, то он больше любого из этих двух углов.

∠АЕО > ∠АСЕ, и так как ∠АЕО = ∠АВО, то ∠АВО > ∠АСЕ.

Что и требовалось доказать. 😎

Как найти угол между прямой и плоскостью

От теории переходим к практике: а как же можно вычислить угол между прямой и плоскостью? Вопрос лёгкий и сложный одновременно. Дело в том, что задач на нахождение угла очень много, и в каждой из них применяется свой алгоритм решения. Большую роль играет предмет и раздел, в котором эта задача приведена: это может быть стереометрия, векторная алгебра и даже физика. Но все эти алгоритмы сводятся к двум методам: геометрическому и алгебраическому или координатному методу. Давайте подробно рассмотрим каждый из них.

Геометрический метод

Чтобы применить геометрический метод, необходимо опустить перпендикуляр на плоскость из точки, принадлежащей исходной прямой. Выясним, чем в этом задании является перпендикуляр, наклонная и проекция, и решим планиметрическую задачку (чаще всего в таких задачах нам будет необходимо найти один из углов прямоугольного треугольника).

Задача 1

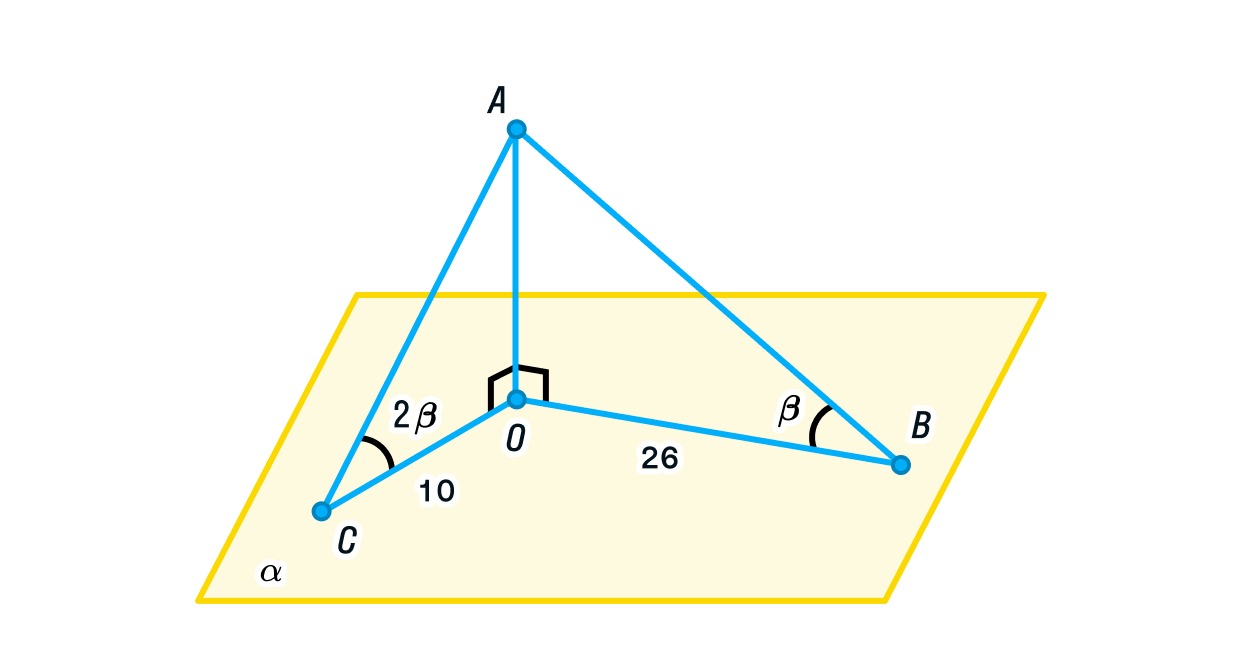
Из точки А на плоскость проведены две наклонные АВ и АС и перпендикуляр АО, причём О, В и С — точки пересечения с плоскостью

.

Определите, чему равен АО, если СО = 10, ВО = 26, а угол АСО в два раза больше угла АВО.

Решение:

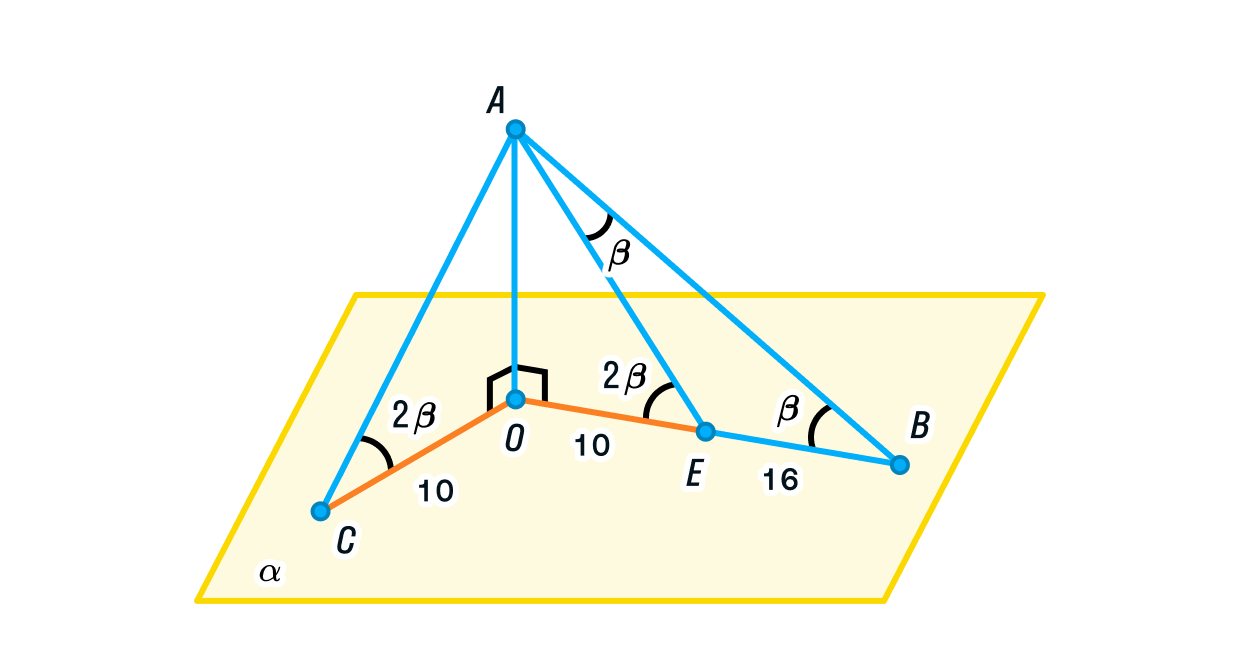
Отметим на стороне ОВ отрезок, равный ОС. Тогда ОС = ОЕ = 10, а ЕВ = 26 – 10 = 16.

Рассмотрим треугольники АСО и АЕО:

• СО = ОЕ (по построению),

• АО — общий катет.

Следовательно, треугольники равны по двум катетам. А значит, угол АСО равен углу АЕО.

Угол АЕО является внешним для треугольника АЕВ, а значит, ∠АЕО = ∠АВЕ + ∠ВАЕ. Так как ∠ АВЕ = , значит, ∠ ВАЕ = 2-=, и треугольник АЕВ — равнобедренный.

Тогда найдём АО через прямоугольный треугольник АОЕ по теореме Пифагора:

.

Ответ:

.

Алгебраический метод

Алгебраический метод или метод координат для нахождения угла между прямой и плоскостью основывается на особой формуле. Чтобы использовать его, необходимо определить координаты двух точек, принадлежащих прямой, описать уравнение плоскости и применить формулу. По сути в этом методе мы находим угол между вектором и плоскостью.

,

где (x₁, y₁, z₁) — это координаты первой точки,

(x₂, y₂, z₂) — координаты второй точки,

А, В и С — это координаты в уравнении плоскости Ax + By + Cz + D = 0.

Иначе эти числа называют координатами вектора нормали плоскости.

Тут может возникнуть вопрос: а что, если в задаче даны не координаты точек, а координаты вектора?

В этом случае вспомним, что координаты вектора находятся через разность координат начала и конца. А значит, мы со спокойно душой подставляем эти координаты в формулу вместо (х₂ – х₁), (y₂ – y₁) и (z₂ – z₁).

В некоторых задачах для нахождения угла между прямой и плоскостью вводят понятие направляющего вектора прямой. Направляющий вектор прямой — это любой вектор, не равный нулю, который размещается на данной прямой или же на прямой, параллельной ей.

Координаты этого вектора можно получить из канонического уравнения прямой:

, где направляющий вектор а имеет координаты (a_x, a_y).

Тогда угол между прямой и плоскостью можно вычислить по формуле:

.

Задача 2

Найдите угол между прямой

и плоскостью 3x – y – z + 1 = 0.

Решение:

1. Определим координаты направляющего вектора для прямой: (2; –1; 3).

2. Определим координаты вектора нормали плоскости: (3; –1; –1).

3. Подставим координаты в формулу для расчёта синуса угла между плоскостью и прямой:

   .

Задача 3

Найдите угол между плоскостью, заданной уравнением x + 2y + 2z – 4 = 0, и прямой, которой принадлежат точки А (0, 2, –1) и В (–2, 4, –1).

Решение:

1. Определим координаты вектора нормали плоскости: (1; 2; 2).

2. Подставим координаты вектора нормали и координаты точек прямой в формулу:

   .

За короткий промежуток времени мы изучили понятие угла между прямой и плоскостью, доказали теоремы, разобрали способы нахождения угла и решили практические задания. Мы — молодцы! 💪

Думаем, вы понимаете, что эта тема очень важна — с её помощью решаются сложные стереометрические задачи, которые встречаются на ОГЭ и ЕГЭ. Подготовиться к таким серьёзным заданиям помогут курсы профильной математики в онлайн-школе Skysmart. На уроках мы сможем более подробно разобрать задачи с пирамидами и параллелепипедами, а ещё научимся составлять уравнения для любой плоскости. Узнать свои сильные и слабые стороны, составить план обучения и познакомиться с онлайн-платформой можно на вводном уроке — это бесплатно.

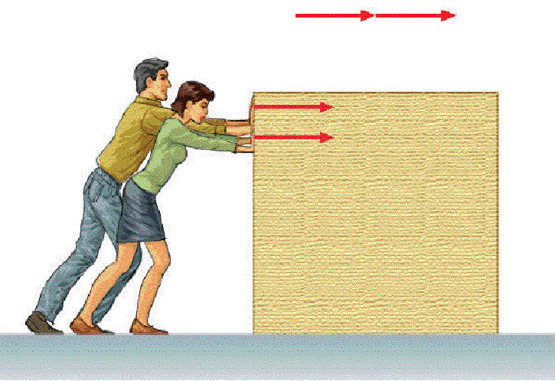
Наклонная плоскость — это плоская поверхность, установленная под углом, отличным от прямого и/или нулевого, к горизонтальной поверхности. Наклонная плоскость позволяет преодолевать значительное сопротивление, прилагая сравнительно малую силу на большем расстоянии, чем то, на которое нужно поднять груз.

Наклонная плоскость — один из широко известных простых механизмов.

Примеры наклонных плоскостей

Примерами наклонных плоскостей служат:

• пандусы и трапы;
• инструменты: стамеска, топор, молоток, плуг, клин и так далее;

Наиболее канонический пример наклонной плоскости — наклонная поверхность, например, въезд на мост с перепадом высоты.

История

Пандусы, или наклонные плоскости, широко использовались при строительстве ранних каменных сооружений, дорог и акведуков. Также они применялись при штурме военных укреплений.

Эксперименты с наклонными плоскостями помогли средневековым физикам (таким, как Галилео Галилей) изучить законы природы, связанные с гравитацией, массой, ускорением и т. д.

Глубокое понимание наклонных плоскостей и их использования помогло прийти к осознанию того, как векторные величины, такие как силы, можно успешно анализировать и управлять ими с помощью математики^{[источник не указан 1035 дней]}. Концепция суперпозиции и декомпозиции очень важна для многих областей современной науки, техники и технологии.

Формулы для наклонной плоскости

здесь  — коэффициент трения тела о поверхность,  — угол наклона плоскости.

Предельным является случай, когда угол наклона плоскости равен 90^o градусам, то есть тело падает, скользя по стене. В этом случае: , то есть сила трения никаким образом не влияет на тело, оно находится в свободном падении. Другим предельным случаем является ситуация, когда угол наклона плоскости равен нулю, т.е. плоскость параллельна земле; в этом случае тело не может двигаться без приложения внешней силы. Надо заметить, что, следуя из определения, в обеих ситуациях плоскость уже не будет являться наклонной — угол наклона не должен быть равен 90^o или 0^o.

Критический угол

Род передвижения тела зависит от критического угла. Тело покоится, если угол наклона плоскости меньше критического угла, покоится или движется равномерно, если угол наклона плоскости равен критическому углу, и движется равноускоренно, при условии что угол наклона плоскости больше критического угла.

Далее описаны все три возможные ситуации, в них:  — коэффициент трения,  — угол наклона плоскости, β — критический угол.

Можно отметить, что .

См. также

• Клин
• Коэффициент трения

Динамика и кинематика — это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I — моменты силы и инерции, соответственно, α — угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀ ± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ — значение начальной скорости тела, S — пройденный за время t путь вдоль прямолинейной траектории. Знак «+» следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак «-«. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀ ± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω — угловые ускорение и скорость, соответственно, θ — угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r — радиус вращения.

Движение по наклонной плоскости: силы

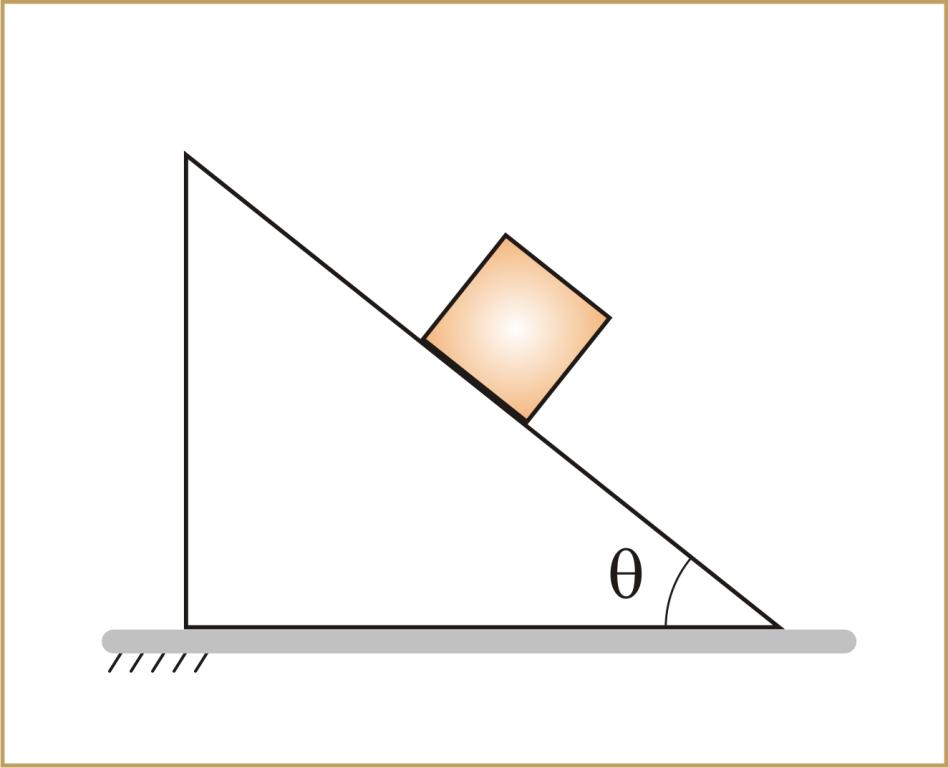
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

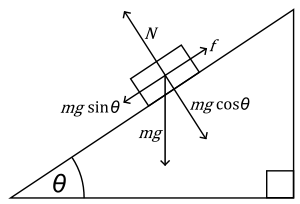
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N — реакция опоры, µ — коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) — µ*m*g*cos(φ) = m*g*(sin(φ) — µ*cos(φ)) = m*a

Здесь φ — это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) — F_r = m*a

Где F_r — сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) — µ*cos(φ)) = m*a =>

a = g*(sin(φ) — µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

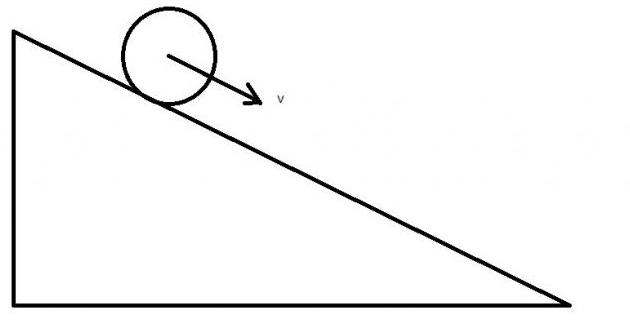
Задача со скатывающимся по плоскости цилиндром

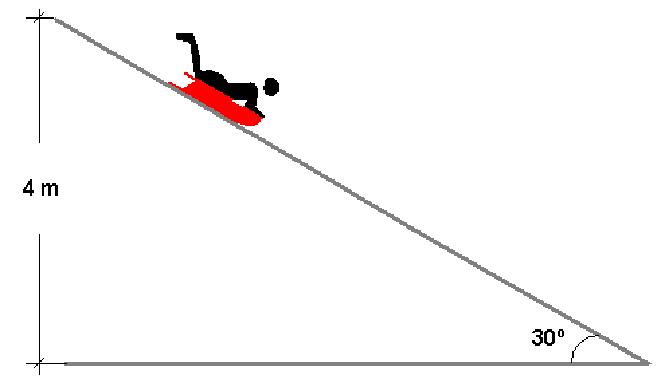
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) — F_r = m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) — 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.