Как найти угол наклона прямой к оси - Исправление недочетов и поиск решений вместе с Examum.ru

Загрузить PDF

Нахождение угла наклона прямой – это один из важнейших навыков в геометрии, необходимый для построения графика линейной функции или для определения координат точек пересечения прямой с осями X и Y. Угол наклона прямой определяет скорость ее роста или убывания,^[1] то есть как быстро прямая перемещается по вертикали в зависимости от движения по горизонтали. Угол наклона прямой легко вычисляется по координатам двух точек, лежащих на этой прямой.

1

Уясните формулу для вычисления углового коэффициента. Угловой коэффициент равен тангенсу угла наклона прямой, который она образует с осью Х, и вычисляется как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между двумя точками.
2

Выберите две точки и найдите их координаты. Можно выбрать любые две точки, лежащие на прямой.
3

Задайте порядок точек (относительно друг друга). Одна точка будет первой точкой, а другая – второй. Не имеет значения, какая точка будет первой, а какая второй – главное не перепутать их порядок в процессе вычисления.^[2]
4

Запишите формулу для вычисления углового коэффициента. Формула: ${frac {VR}{GR}}={frac {y_{{2}}-y_{{1}}}{x_{{2}}-x_{{1}}}}$ , где VR – вертикальное расстояние, определяемое изменением координаты «у», GR – горизонтальное расстояние, определяемое изменением координаты «х».^[3]

Реклама

1

В формулу для вычисления углового коэффициента подставьте координаты «у». Не перепутайте их с координатами «х» и убедитесь, что подставляете правильные координаты первой и второй точек.
2

В формулу для вычисления углового коэффициента подставьте координаты «х». Не перепутайте их с координатами «у» и убедитесь, что подставляете правильные координаты первой и второй точек.
3

Вычтите координаты «у». Вы найдете вертикальное расстояние.
4

Вычтите координаты «х». Вы найдете горизонтальное расстояние.
5

Если возможно, сократите дробь. Вы найдете угловой коэффициент.
6
Обращайте внимание на отрицательные числа. Угловой коэффициент может быть положительным или отрицательным. В случае положительного значения прямая возрастает (движется вверх слева направо); в случае отрицательного значения прямая убывает (движется вниз слева направо).
- Помните, что если и в числителе, и в знаменателе стоят отрицательные числа, то результат будет положительным.
- Если в числителе или в знаменателе стоит отрицательное число, то результат будет отрицательным.
7
Проверьте ответ. Для этого измерьте или посчитайте (по шкалам осей) вертикальное и горизонтальное расстояния. Если они совпали с вычисленными, то ответ правильный.
- Если измеренные или посчитанные вертикальное и горизонтальное расстояния не совпали с вычисленными, то ответ не правильный.
Реклама

Советы

Об этой статье

Эту страницу просматривали 90 508 раз.

Была ли эта статья полезной?

Источник

Угол наклона прямой

Решение функций

Для построения графика линейной функции или определения координат точек пересечения прямой с осью Ох и Оy важно уметь находить угол наклона прямой.

Углом наклона прямой к оси Ох является угол, который считают против часовой стрелки от положительного направления Ох к прямой.

В уравнении y = kх + b, где b — координата «у» — точки пересечения прямой с Оy, коэффициент k при х — коэффициент наклона прямой.
Этот коэффициент равняется тангенсу угла а, образованного между прямой и положительным направлением оси Ох: k = tg а.

Если прямая наклонена вправо, то угол, образованный между прямой и осью Ох, будет острым, тангенс угла (tgа) и коэффициент наклона k больше нуля. Угол определяем по формуле: a = arctg k.

Если наклон прямой влево, то угол между прямой и осью Ох будет тупым, а тангенс угла (tgа) и коэффициент k меньше нуля. Угол a = Пи — arctg |k|.

Угол наклона равняется 0, если прямая расположена параллельно Ох или совпадает с ней.

Зная координаты 2-х точек, расположенных на прямой, можно легко рассчитать угол наклона как отношение вертикального расстояния между двумя точками к горизонтальному расстоянию между ними.

Пусть координаты первой точки (х1,y1), координаты второй (х2,y2), тогда угловой коэффициент будет равняться: (y2 — y1): (х2 — х1),
где (y2 — y1) — величина изменения координаты «у», (х2 — х1) — изменение координаты «х». Из полученной величины возьмем арктангенс и определим угол наклона прямой.

Быстро определить угол наклона прямой, вам поможет онлайн калькулятор.

Источник

Калькулятор углового коэффициента прямой может не только рассчитать коэффициент, но и найдет точки пересечения прямой с осями абсцисс и ординат (x и y), а также покажет решение и построит график прямой.

Содержание:

калькулятор углового коэффициента прямой
определение углового коэффициента прямой
формула углового коэффициента прямой
геометрический смысл углового коэффициента
1. k>0
2. k<0
3. k=0
4. k не определен (k=∞)
5. угловой коэффициент параллельных прямых
6. угловой коэффициент перпендикулярных прямых
примеры расчета углового коэффициента прямой по заданным координатам точек

Определение углового коэффициента прямой

Угловой коэффициент прямой — это число, которое определяет наклон прямой относительно положительного направления оси OX. Численно он равен тангенсу угла (отсчитываемого против часовой стрелки) между положительным направлением оси OX и прямой.

Угловой коэффициент прямой обозначается буковой k.

Угловой коэффициент показывает, как быстро прямая меняет свое положение по оси OX при изменении координаты y и является ключевым понятием в геометрии и физике, используемым для описания многих физических явлений, например, движения тела в пространстве или распространение света.

В геометрии, угловой коэффициент прямой используется для определения угла наклона прямой относительно оси абсцисс и для вычисления ее точек пересечения с осями координат. Также угловой коэффициент прямой используется для записи уравнения прямой в общем виде. Знание углового коэффициента прямой является необходимым при решении многих задач геометрии, таких как построение перпендикуляров и параллельных линий, определение углов между прямыми и плоскостями, а также решение задач на поиск расстояний между прямыми и плоскостями.

Формула углового коэффициента прямой

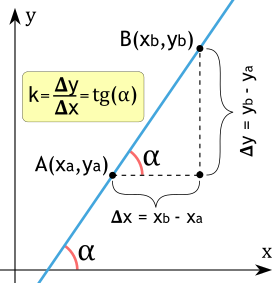
Формула вычисления углового коэффициента прямой определяется как отношение изменения координаты y к изменению координаты x между любыми двумя точками на прямой. Математически это можно записать следующим образом:

{k=dfrac{y_b — y_a}{x_b — x_a} = tg(alpha)}

k — угловой коэффициент прямой,

x_a, y_a — координаты точки A,

x_b, y_b — координаты точки B

α — угол между осью OX и прямой (против часовой стрелки).

Если прямая задана уравнением в общем виде y = kx + b, то угловой коэффициент прямой равен коэффициенту при x, то есть k.

Геометрический смысл углового коэффициента прямой

Рассмотрим возможные значения углового коэффициента и какой геометрический смысл он несет.

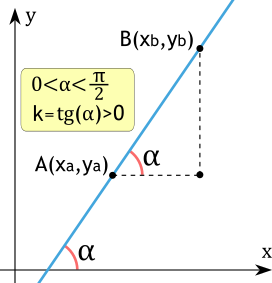
Угловой коэффициент прямой больше нуля

Если угловой коэффициент прямой больше нуля (k>0), то угол между осью OX и прямой является острым, а график прямой возрастающий. Обратное утверждение также справедливо — если график прямой возрастает, то ее угловой коэффициент больше нуля.

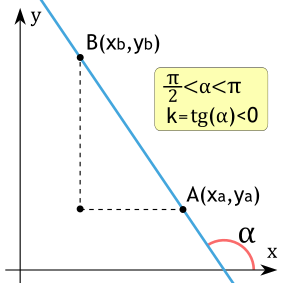
Угловой коэффициент прямой меньше нуля

Если угловой коэффициент прямой меньше нуля (k<0), то угол между осью OX и прямой является тупым, а график прямой убывающий. И наоборот — если график прямой убывает, то ее угловой коэффициент меньше нуля.

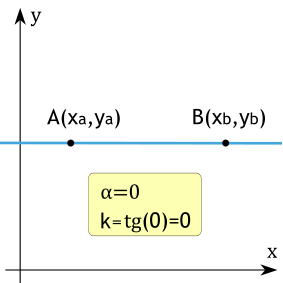
Угловой коэффициент равен нулю

Если угловой коэффициент прямой равен нулю (k=0), то это значит, что прямая параллельна оси x.

Угловой коэффициент не определен (равен бесконечности)

Если угловой коэффициент прямой не определен (или можно сказать обращается в бесконечность) (k=∞), то это значит, что прямая параллельна оси y.

Угловой коэффициент параллельных прямых

Если прямые параллельны, то их угловые коэффициенты равны и наоборот — если у прямых равные угловые коэффициенты, то они параллельны друг другу.

Угловой коэффициент перпендикулярных прямых

Если прямые перпендикулярны, то их угловые коэффициенты обратно пропорциональны и имеют противоположный знак.

Для примера рассмотрим две прямые, заданные угловыми коэффициентами:

y = k_{m} x + b_m

y = k_{n} x + b_n

Прямые будет перпендикулярны, если k_{m} = — dfrac{1}{k_{n}}

Как рассчитать угловой коэффициент прямой по заданным координатам точек

Чтобы закрепить материал, рассмотрим решение задачи.

Задача 1

Найдите угловой коэффициент прямой, проходящей через точки A(5, -2) и B(-3, 1).

Решение

Воспользуемся формулой углового коэффициента прямой. Для начала найдем разницу между соответствующими координатами двух точек:

{Delta x = x_b — x_a = -3 -5 -= -8}

{Delta y = y_b — y_a = 1 — -(2) = 3}

Осталось применить формулу и поделить Delta y на Delta x:

k = dfrac{Delta y}{Delta x} = dfrac{3}{-8} = — dfrac{3}{8} approx -0.375

Это и есть угловой коэффициент прямой AB.

А если вы внимательно читали статью, то, учитывая, что полученный угловой коэффициент отрицательный, можно сказать, что прямая AB убывающая.

Ответ: k = — dfrac{3}{8} approx -0.375

Проверить ответ нам поможет калькулятор .

Источник

Что такое линейная функция и как выглядит ее график мы подробно разбирали здесь.

В этой статье мы остановимся на том, как находить коэффициент наклона прямой.

Как мы знаем, уравнение прямой имеет вид y=kx+b . В этом уравнении коэффициент при отвечает за наклон прямой и называется коэффициентом наклона. Он равен тангенсу угла между прямой и положительным направлением оси .

Внимание! Не просто между прямой и осью , а именно между прямой и положительным направлением оси .

Например, в прямой y=3x-1 коэффициент наклона равен , в прямой y=2-5x коэффициент наклона равен .

В уравнении прямой y=-1 слагаемое, содержащее отсутствует, следовательно, коэффициент при равен нулю. Угол наклона этой прямой к оси равен нулю — прямая y=-1 параллельна оси .

Если прямая наклонена вправо, то угол между прямой и положительным направлением оси — острый, соответственно, тангенс этого угла больше нуля, и коэффициент k>0 .

Например:

Здесь

Если прямая наклонена влево, то угол между прямой и положительным направлением оси — тупой, соответственно, тангенс этого угла меньше нуля, и коэффициент k<0 :

Здесь .

Решим две задачи на нахождение коэффициента наклона прямой.

1. Найдите угловой коэффициент прямой, проходящей через точки с координатами (-1;-1) и (1;3).

Решим эту задачу двумя способами.

А). Так как прямая проходит через точки (-1;-1) и (1;3), координаты этих точек удовлетворяют уравнению прямой y=kx+b . То есть если мы координаты каждой точки подставим в уравнение прямой, то получим верное равенство. Так как у нас две точки, получаем систему:

или

Вычтем из второго уравнения первое, и получим 2k=4 , отсюда k=2 .

Б). Построим график этой функции. Для этого нанесем данные точки А(-1;-1) и В(1;3) на координатную плоскость и проведем через них прямую:

Коэффициент равен тангенсу угла наклона между прямой и положительным направлением оси , на чертеже это угол alpha :

Чтобы найти рассмотрим прямоугольный треугольник АВС с вершинами в данных точках.

Угол beta прямоугольного треугольника АВС равен углу alpha (соответственные углы, полученный при пересечении параллельных прямых АС и ОХ секущей АВ):

равен отношению противолежащего катета к прилежащему, то есть

Отсюда

2. Найдите угловой коэффициент прямой, проходящей через точки с координатами (4;0) и (0;8).

Решение с помощью системы уравнений абсолютно аналогично решению предыдущей задачи, можете воспроизвести его самостоятельно.

Выполним это задание с помощью графика.

Нанесем данные токи на координатную плоскость и проведем через них прямую:

Угол между прямой и положительным направлением оси ОХ — это угол alpha :

Коэффициент наклона прямой . Чтобы найти , построим прямоугольный треугольник ВОА:

В этом прямоугольном треугольнике угол alpha — внешний. Мы можем найти тангенс внутреннего угла beta . .

. Отсюда .

Еще раз! Если прямая наклонена влево, то коэффициент наклона прямой отрицательный.

И.В. Фельдман, репетитор по математике.

Источник

В декартовых координатах каждая прямая
определяется уравнением первой степени
и, обратно, каждое уравнение первой
степени определяет прямую.

Уравнение
вида

(1)

называется
общим уравнением прямой.

Угол ,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:

Уравнение называется
уравнением прямой с угловым коэффициентом;
k — угловой коэффициент, b — величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.

Если
прямая задана общим уравнением

то
ее угловой коэффициент определяется
по формуле

Уравнение является
уравнением прямой, которая проходит
через точку (, )
и имеет угловой коэффициент k.

Если
прямая проходит через точки (, ), (, ),
то ее угловой коэффициент определяется
по формуле

Уравнение

является
уравнением прямой, проходящей через
две точки (, )
и (, ).

Если
известны угловые коэффициенты и двух
прямых, то один из углов между
этими прямыми определяется по формуле

Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:.

Признаком
перпендикулярности двух прямых является
соотношение
,
или .

Иначе говоря, угловые коэффициенты
перпендикулярных прямых обратны по
абсолютной величине и противоположны
по знаку.

4.Общее уравнение прямой

Уравнение

Ах+Ву+С=0

(где А, В, Смогут иметь любые
значения, лишь бы коэффициентыА,
Вне были нулями оба сразу)
представляетпрямую
линию. Всякую прямую можно
представить уравнением этого вида.
Поэтому его называютобщим уравнением
прямой.

Если А=0, то есть уравнение не
содержитх, то оно представляет
прямую,параллельную
оси ОХ.

Если В=0, то есть уравнение не
содержиту, то оно представляет
прямую,параллельную
оси ОY.

Когла Вне равно нулю, то общее
уравнение прямой можноразрешить
относительно ординаты у,
тогда оно преобразуется к виду

y=ax+b

(где a=-A/B; b=-C/B).

Аналогично, при Аотличным от
нуля общее уравнение прямой можно
разрешить относительнох.

Если С=0, то есть общее уравнение
прямой не содержит свободного члена,
то оно представляет прямую, проходящую
через начало координат

5. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом

Уравнение прямой, проходящей
через данную точку A(x₁, y₁)
в данном направлении, определяемом
угловым коэффициентом k,

y — y₁ = k(x — x₁). (1)

Это уравнение определяет
пучок прямых, проходящих через
точку A(x₁, y₁),
которая называется центром пучка.

6. уравнение прямой,
проходящей через две данные точки.

. Уравнение
прямой, проходящей через две точки: A(x₁, y₁)
и B(x₂, y₂),
записывается так:

(2)

Угловой коэффициент прямой, проходящей
через две данные точки, определяется
по формуле

(3)

7.
Уравнение прямой в отрезках

Если в общем уравнении
прямой ,
то разделив (1) на ,
получаем уравнение прямой в отрезках

где  ,  .
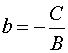
Прямая пересекает ось   в
точке  ,
ось   в
точке  .

8.
Формула: Угол между прямыми на плоскости

Уголα между
двумя прямыми, заданными
уравнениями: y=k₁x+b₁ (первая
прямая) и y=k₂x+b₂ (вторая
прямая), может быть вычислен по формуле
(угол отсчитывается от 1^й прямой
ко 2^й против
часовой стрелки):

tg(α)=(k₂-k₁)/(1+k₁k₂)

9. Взаимное
расположение двух прямых на плоскости.

Пусть сейчас
оба уравнения прямых
записаны в общем виде.

Теорема. Пусть

– общие уравнения двух
прямых на координатной плоскости
Оху. Тогда

1) если ,
то прямые и совпадают;

2) если ,
то прямые и

параллельные;

3) если ,
то прямые пересекаются.

Доказательство.
Условие равносильно
коллинеарности нормальных векторов данных
прямых:

.
Поэтому, если ,
то и прямыепересекаются.

Если же ,
то , , иуравнение прямой принимает
вид:

или ,
т.е. прямые совпадают.
Заметим, что коэффициент пропорциональности ,
иначе все коэффициенты общего уравнения были
бы равны нулю, что невозможно.