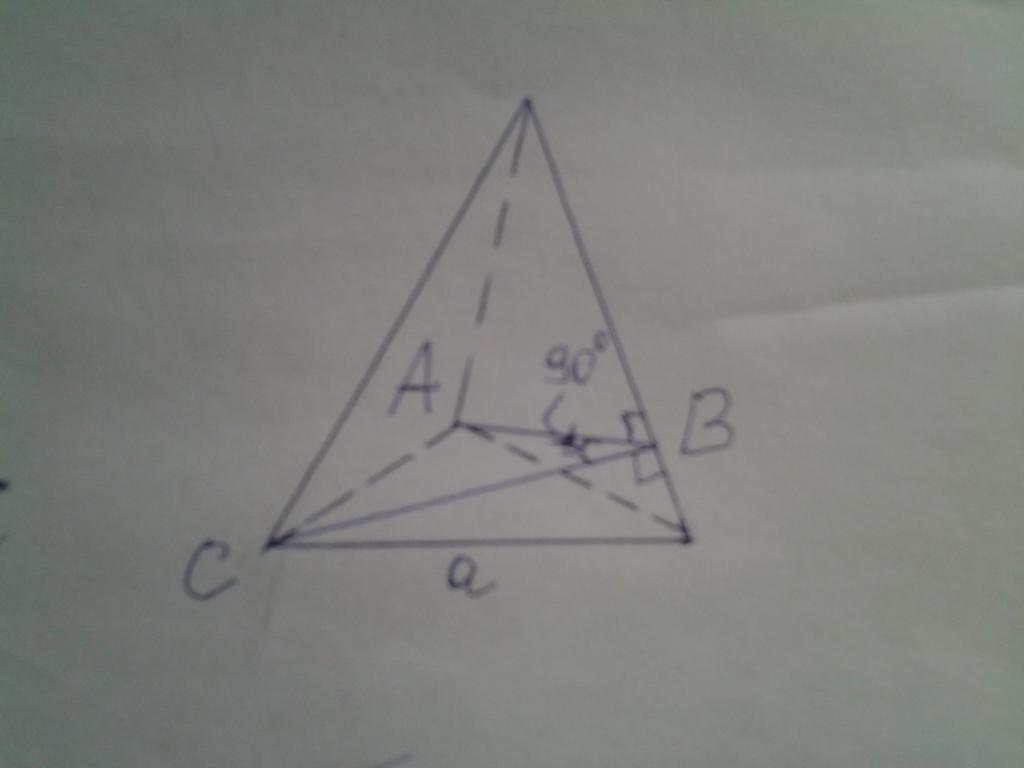Как найти угол наклона ребра к плоскости

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания.

Треугольник, у которого все сторны равны, называется правильным.

Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром правильного треугольника.

В правильном треугольнике медиана, высота и биссектриса, проведённые к основанию, совпадают.

Высота треугольника — перпендикуляр, проведённый из вершины треугольника к основанию.

В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов

Тангенс угла tg(A) — есть отношение противолежащего катета a к прилежащему катету b

Задача

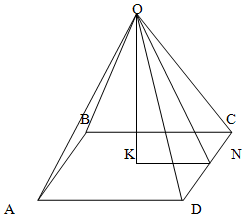
В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.
Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.

Найдем угол наклона ребер к плоскости основания.
Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это — квадрат. Поскольку высота пирамиды проецируется в центр основания, то это — точка пересечения диагоналей. Откуда KN = а/2

Треугольник OKN — прямоугольный, OK — высота, равная 3а.
Найдем тангенс угла KNO, обозначив его как α .

tg α = OK / KN
tg α = 3a / (a/2) = 6
α = arctg 6 ≈ 80.5377°

Найдем угол наклона ребра пирамиды.
Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.

Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как β ) равен

tg β = OK / KC
tg β = 3a / (а√2/2) = 6 / √2
β = arctg 6/√2 ≈ 76.7373°

Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°

Двугранные углы пирамиды и методика их расчета

Типичными линейными параметрами любой пирамиды являются длины сторон ее основания, высота, боковые ребра и апофемы. Тем не менее существует еще одна характеристика, которая связана с отмеченными параметрами, — это двугранный угол. Рассмотрим в статье, что он собой представляет и как его находить.

Пространственная фигура пирамида

Каждый школьник хорошо представляет, о чем идет речь, когда слышит слово «пирамида». Геометрически построить ее можно так: выбрать некоторый многоугольник, затем зафиксировать точку в пространстве и соединить ее с каждым углом многоугольника. Получившаяся объемная фигура будет пирамидой произвольного типа. Многоугольник, который ее образует, называется основанием, а точка, с которой соединены все его углы, является вершиной фигуры. Ниже на рисунке схематически показана пятиугольная пирамида.

Вам будет интересно: Популяция людей: определение, виды, свойства и примеры

Видно, что ее поверхность образована не только пятиугольником, но и пятью треугольниками. В общем случае число этих треугольников будет равно количеству сторон многоугольного основания.

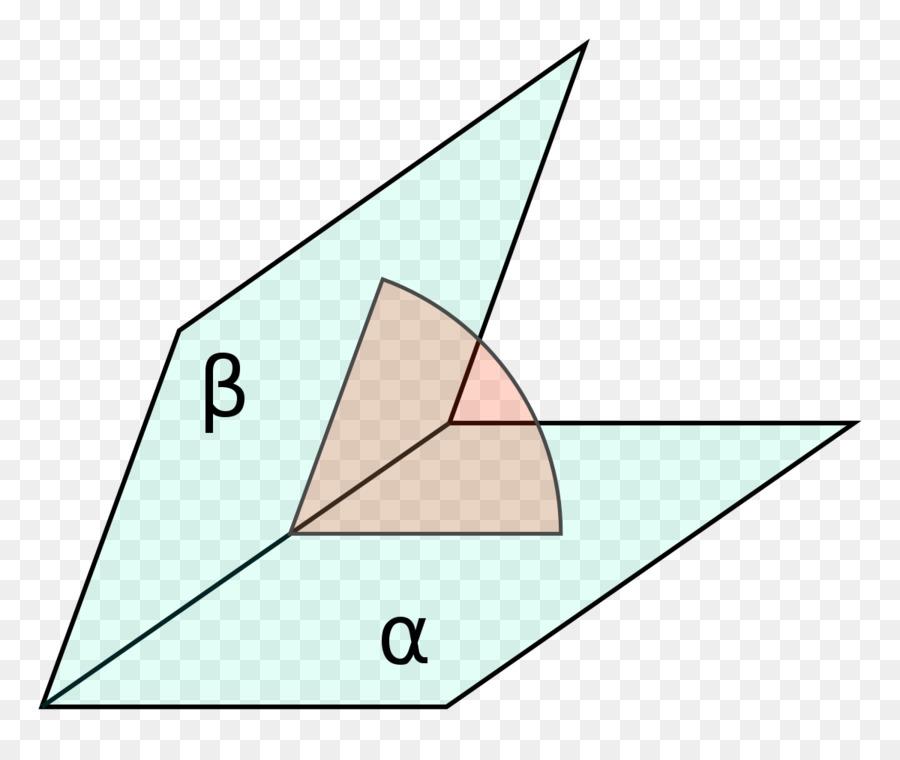
Двугранные углы фигуры

Вам будет интересно: «Дурачок» или «дурачек»: как не проспорить в Интернете из-за орфографии?

Когда рассматриваются геометрические задачи на плоскости, то любой угол образован двумя пересекающимися прямыми, или отрезками. В пространстве же к этим линейным углам добавляются двугранные, образованные пересечением двух плоскостей.

Если отмеченное определение угла в пространстве применить к рассматриваемой фигуре, то можно сказать, что существует два вида двугранных углов:

• При основании пирамиды. Он образован плоскостью основания и любой из боковых граней (треугольником). Это означает, что углов при основании у пирамиды n, где n — число сторон многоугольника.
• Между боковыми сторонами (треугольниками). Количество этих двугранных углов также составляет n штук.

Заметим, что первый тип рассматриваемых углов строится на ребрах основания, второй тип — на боковых ребрах.

Как рассчитать углы пирамиды?

Линейный угол двугранного угла является мерой последнего. Вычислить его непросто, поскольку грани пирамиды, в отличие от граней призмы, пересекаются не под прямыми углами в общем случае. Надежнее всего проводить расчет значений двугранных углов с использованием уравнений плоскости в общем виде.

В трехмерном пространстве плоскость задается следующим выражением:

A*x + B*y + C*z + D = 0

Где A, B, C, D — это некоторые действительные числа. Удобством этого уравнения является то, что первые три отмеченных числа являются координатами вектора, который перпендикулярен заданной плоскости, то есть:

Если известны координаты трех точек, принадлежащих плоскости, то, взяв векторное произведение двух векторов, построенных на этих точках, можно получить координаты n¯. Вектор n¯ называется направляющим для плоскости.

Согласно определению, двугранный угол, образованный пересечением двух плоскостей, равен линейному углу между их направляющими векторами. Предположим, что мы имеем две плоскости, нормальные векторы которых равны:

Для вычисления угла φ между ними можно воспользоваться свойством произведения скалярного, тогда соответствующая формула принимает вид:

Или в координатной форме:

φ = arccos(|A1*A2 + B1*B2 + C1*C2|/(√(A12 + B12+C12)*√(A22 + B22 + C22)))

Покажем, как использовать изложенную методику расчета двугранных углов при решении геометрических задач.

Углы правильной пирамиды четырехугольной

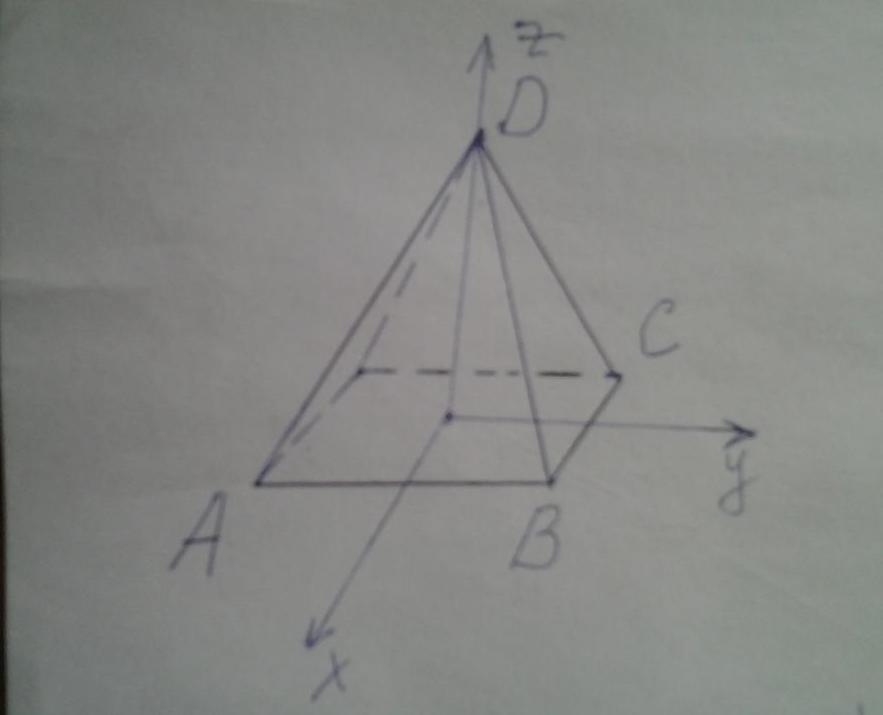
Предположим, что имеется правильная пирамида, в основании которой находится квадрат со стороной 10 см. Высота фигуры равна 12 см. Необходимо вычислить, чему равны двугранные углы при основании пирамиды и для ее боковых сторон.

Поскольку заданная в условии задачи фигура является правильной, то есть обладает высокой симметрией, то все углы при основании равны друг другу. Также являются одинаковыми углы, образованные боковыми гранями. Чтобы вычислить необходимые двугранные углы, найдем направляющие векторы для основания и двух боковых плоскостей. Обозначим длину стороны основания буквой a, а высоту h.

Рисунок выше показывает четырехугольную правильную пирамиду. Выпишем координаты точек A, B, C и D в соответствии с введенной системой координат:

Теперь найдем направляющие векторы для плоскостей основания ABC и двух боковых сторон ABD и BCD в соответствии с изложенной в пункте выше методикой:

Теперь остается применить соответствующую формулу для угла φ и подставить значения стороны и высоты из условия задачи:

Угол между ABC и ABD:

Угол между ABD и BDC:

φ = arccos(a4/(4*a2*(h2+a2/4)) = arccos(a2/(4*(h2+a2/4))) = 81,49o

Мы вычислили значения углов, которые требовалось найти по условию задачи. Полученные при решении задачи формулы можно использовать для определения двугранных углов четырехугольных правильных пирамид с любыми значениями a и h.

Углы треугольной правильной пирамиды

На рисунке ниже дана пирамида, основанием которой является правильный треугольник. Известно, что двугранный угол между боковыми сторонами является прямым. Необходимо вычислить площадь основания, если известно, что высота фигуры равна 15 см.

Двугранный угол, равный 90o, на рисунке обозначен как ABC. Решить задачу можно, применяя изложенную методику, однако в данном случае поступим проще. Обозначим сторону треугольника a, высоту фигуры — h, апофему — hb и боковое ребро — b. Теперь можно записать следующие формулы:

Поскольку два боковых треугольника в пирамиде являются одинаковыми, то стороны AB и CB равны и являются катетами треугольника ABC. Обозначим их длину x, тогда:

Приравнивая площади боковых треугольников и подставляя апофему в соответствующее выражение, имеем:

Площадь равностороннего треугольника рассчитывается так:

Подставляем значение высоты из условия задачи, получаем ответ: S = 584,567 см2.

Пирамида и ее элементы

Здесь собраны основные сведения о пирамидах и связанных с ней формулах и понятиях. Все они изучаются с репетитором по математике при подготовке к ЕГЭ.

Рассмотрим плоскость , многоугольник , лежащий в ней и точку S, не лежащую в ней. Соединим S со всеми вершинами многоугольника. Полученный при этом многогранник называется пирамидой. Отрезки называются боковыми ребрами. Многоугольник называется основанием, а точка S — вершиной пирамиды. В зависимости от числа n пирамида называется треугольной (n=3), четырехугольной (n=4), птяиугольной (n=5) и так далее. Альтернативное название треугольной пирамиды – тетраэдр. Высотой пирамиды называется перпендикуляр, опущенный из ее вершины к плоскости основания.

Пирамида называется правильной, если правильный многоугольник, а основание высоты пирамиды (основание перпендикуляра) является его центром.

Комментарий репетитора:
Не путайте понятие «правильная пирамида» и «правильный тетраэдр». У правильной пирамиды боковые ребра совсем не обязательно равны ребрам основания, а в правильном тетраэдре все 6 ребер ребра равные. Это его определение. Легко доказать, что из равенства следует совпадение центра P многоугольника с основанием высоты, поэтому правильный тетраэдр является правильной пирамидой.

Что такое апофема?
Апофемой пирамиды называется высота ее боковой грани. Если пирамида правильная, то все ее апофемы равны. Обратное неверно.

Репетитор по математике о своей терминологии: работа с пирамидами на 80% строится через два вида треугольников:
1) Содержащий апофему SK и высоту SP
2) Содержащий боковое ребро SA и его проекцию PA

Чтобы упростить ссылки на эти треугольники репетитору по математике удобнее называть первый из них апофемным, а второй реберным. К сожалению, этой терминологии вы не встретите ни в одном из учебников, и преподавателю приходится вводить ее в одностороннем порядке.

Формула объема пирамиды:
1) -высота пирамиды
2) – радиус вписанного шара, а – площадь полной поверхности пирамиды.
3) – площадь параллелограмма, образованного серединами четырех оставшихся ребер.

Свойство основания высоты пирамиды:

Точка P (смотри рисунок) совпадает с центром вписанной окружности в основание пирамиды, если выполняется одно из следующих условий:
1) Все апофемы равны
2) Все боковые грани одинаково наклонены к основанию
3) Все апофемы одинаково наклонены к высоте пирамиды
4) Высота пирамиды одинаково наклонена ко всем боковым граням

Комментарий репетитора по математике: обратите внимание, что все пункты объединяет одно общее свойство: так или иначе везде участвуют боковые грани (апофемы — это их элементы). Поэтому репетитор может предложить менее точную, но более удобную для заучивания формулировку: точка P совпадает с центром вписанной окружности основание пирамиды, если имеется любая равная информация о ее боковых гранях. Для доказательства достаточно показать, что все апофемные треугольники равны.

Точка P совпадает с центром описанной около основания пирамиды окружностью, если верно одно их трех условий:
1) Все боковые ребра равны
2) Все боковые ребра одинаково наклонены к основанию
3) Все боковые ребра одинаково наклонены к высоте

Комментарий репетитора. Аналогично предыдущему пункту текст можно упростить и вместо этих условий произнести : «если имеется любая равная информация о боковых ребрах». При этом все апофемные треугольники будут равны все проекции боковых ребер будет равны P будет равноудалена от всех вершин основания и поэтому окажется центром описанной окружности.

Площадь полной поверхности пирамиды:
Полощадью поверности пирамиды называется сумма площадей всех ее граней .
Если все апофемы равны (например в правильной пирамиде), то площадь ее боковой поверхности вычисляется по формуле , где p — полупериметр основания, а SK-апофема.

Правильная треугольная пирамида однозначно определяется двумя параметрами: один плоский, а другой пространственный: к плоскому я отношу любой элемент правильного треугольника (кроме угла), а к пространственному любой связующий параметр между основанием и точкой S: апофема, высота, углы наклона ребер, граней, объем, площадь поверхности и др. При наличие в условии задачи этих двух начальных данных репетитор с учеником может найти у такой пирамиды все что угодно.

Пирамида — обязательный пункт подготовки к ЕГЭ по математике. Програмный минимум по стереометрии включает в себя все вышеуказанные сведения, кроме третьей формулы вычисления объема пирамиды.

Колпаков Александр,
репетитор по математике в Москве. Строгино

Для
определения истинных размеров ребер
многогранников и углов наклона ребер
к плоскости проекций можно воспользоваться
тремя способами:

• способом
  прямоугольного треугольника;

• способом
  перемены плоскостей проекции;

• способом
  вращения вокруг оси, перпендикулярной
  к плоскости

проекции.

Рассмотрим
применение данных способов на примере
определения натуральных величин ребер
и их углов наклона к плоскостям проекций
для треугольной пирамиды SABC
(рис. 6а).

Основание
АВС
пирамиды лежит в горизонтальной плоскости
уровня. Поэтому его стороны па П₁
проецируются в натуральную величину.
Ребра SА, SB,
SC пирамиды
относительно плоскостей проекций
изображены с искажением, так как это
отрезки прямых общего положения.
Определим натуральные величины ребер
и углы наклона этих ребер к плоскостям
проекций.

Способ
прямоугольного треугольника.

Для
установления зависимости между
натуральной величиной отрезка прямой
и его проекциями на комплексном чертеже
достаточно построить прямоугольный
треугольник, взяв за один его катет
горизонтальную (фронтальную, профильную)
проекцию отрезка, а за другой катет
разницу – расстояний концов отрезка
до горизонтальной (или соответственно
фронтальной, профильной) плоскости
проекций.

На
рис. 6а
показано определение натуральной
величины ребра SС
и его угла наклона к плоскости проекций
П₁.
Приняв S₁С₁
за катет прямоугольного треугольника,
и восстановив из точки S₁
перпендикуляр S₁S₀,
равный по величине разности Z_S
– Z_C
=
Z
(разницу
замеряем на фронтальной проекции),
получим на горизонтальной плоскости
проекций прямоугольный 
S₁C₁S₀.
Гипотенуза этого треугольника равна
натуральной величине ребра SC,
а угол, образованный гипотенузой C₁S
₀ с катетом
S₁C₁
– 
натуральная величина угла наклона ребра
SC
к плоскости проекций П₁.

а)
б)

Рис.6

Способ перемены
плоскостей проекций.

Особенностью
способа перемены плоскостей проекций,
является переход от одной системы
(старой), в которой заданы проекции
объекта, к новой системе взаимно-перпендикулярных
плоскостей, выбранных определенным
образом.

Например,
для определения натуральной величины
ребра SА
пирамиды SABC
(рис. 6б) новая плоскость проекций П₄
должна быть расположена параллельно
ему (П₄
||
SА)
и перпендикулярно плоскости проекций
П₁
(П₄

П₁).
Новая ось проекций Х₁₄
располагается параллельно проекции S₁
А₁.
Затем через проекции А₁
и S₁
точек А
и S
проводим новые линии связи и откладываем
на них высоты точек А
и S
(Z_А,
Z_S),
строим новые проекции А₄
и S₄.
Соединим эти точки, получим новую
проекцию ребра А₄S₄,
которое в новой системе плоскостей
проекции (П₁
/ П₄)
стало линией уровня. Следовательно,
проекция ребра А₄S₄
равна
натуральной величине ребра АS,
а угол 
равен углу наклона ребра к плоскости
проекций П₁.

Для
определения натуральной величины ребра
SА
пирамиды SABC
(рис. 6б) может быть применена новая
плоскость проекций П₅.
Плоскость проекций П₅
должна
быть расположена параллельно SА
(П₅
||
SА)
и перпендикулярно плоскости проекций
П₂
(П₅

П₂).
Новая ось проекций Х₂₅
располагается параллельно проекции
S₂А₂.
Далее построения выполняются аналогично,
рассмотренным выше.

Способ
вращения вокруг оси, перпендикулярной
к плоскости проекций.

Способ
вращения нагляден и в ряде случаев
наиболее удобен для определения
натуральных величин отрезков и углов
наклона прямой к плоскости. Отрезок
проецируется без искажения, если в
результате перемещения он станет
параллельным какой-либо из плоскостей
проекций. При этом вращение отрезка
должно осуществляться таким образом,
чтобы угол наклона прямой к одной из
плоскостей проекций не изменялся.
Последнее требование вынуждает вращать
отрезок вокруг осей, перпендикулярных
к плоскостям проекций.

Пусть,
например, требуется определить натуральную
величину ребра SА
пирамиды SABC
(рис. 6а).

Сокращая
количество построений, проведем ось
i(i_1,i₂)
через один из концов ребра – через точку
S.
Из точки S₁
радиусом S₁А₁
описываем дугу окружности до пересечения
с прямой, проведенной из точки S₁
параллельно оси Х₁₂
. Точка пересечения А₁
– новая
горизонтальная проекция точки А.
Фронтальную проекцию А₁
точки А
находим, проведя вертикальную линию
связи из точки
до пересечения с прямой, проведенной
из точки А₂
параллельно оси Х₁₂.
Соединив точки А₂
и S₂
на плоскости П₂,
получим натуральную величину длины
S₂А₂
ребра SА,
а угол 
есть угол наклона ребра к плоскости П₂.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Примечание. Это урок с решениями задачам по геометрии (раздел стереометрия, пирамида с четырехугольником в основании). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. В задачах вместо символа «квадратный корень» применяется функция sqrt(), в которой sqrt — символ квадратного корня, а в скобках указано подкоренное выражение. Для простых подкоренных выражений может использоваться знак «√».

Задача

В правильной четырёхугольной пирамиде сторона основания равна а, высота равна 3а.

Найдите углы наклона боковых рёбер и боковых граней к плоскости основания.

Решение.



Найдем угол наклона ребер к плоскости основания.

Поскольку в основании правильной пирамиды лежит правильный четырехугольник, то, в данном случае, это — квадрат. Поскольку высота пирамиды проецируется в центр основания, то это — точка пересечения диагоналей. Откуда KN = а/2

Треугольник OKN — прямоугольный, OK — высота, равная 3а.

Найдем тангенс угла KNO, обозначив его как

α.

tg

α = OK / KN

tg α = 3a / (a/2) = 6

α = arctg 6 ≈ 80.5377°

Найдем угол наклона ребра пирамиды.

Диагональ квадрата со стороной а равна а√2. Поскольку высота проецируется в центр основания, то в этой точке диагонали делятся пополам.

Таким образом, для прямоугольного треугольника OKC тангенс угла KCO (обозначим его как

β ) равен

tg

β = OK / KC

tg β = 3a / (а√2/2) = 6 / √2

β = arctg 6/√2 ≈ 76.7373°

Ответ: угол наклона граней arctg 6 ≈ 80.5377°; угол наклона ребер arctg 6/√2 ≈ 76.7373°

0
 

 Правильная пирамида с четырехугольником в основании (часть 3) |

Описание курса

| Нахождение величины наклона боковых граней правильной прамиды 

Очень просто. Для этого достаточно знать, что на любой окружности можно отметить

лишь 6 точек без остатка, на расстоянии равном радиусу этой оеружности.

Если эти точки соединить прямыми линиями — получим правильный вписанный шестиугольник сторона которого равна радиусу этой окружности.

Теперь, можем смело разрезать (рассечь) нашу призму, через вершину и две

противолежащие верщины шести угольника — в сечении получим треугольник

со сторонами 6м, 6м и основанием равным двум радиусам 3+3=6м.

В итоге выясняется, что все стороны треугла равны — а у равностороннего треугла,

из основ геометрии извесно, что все углы равны меж собой, и равны 60 градусам.

Отсюда и угол наклона ребра к основанию призмы = 60 градусам.