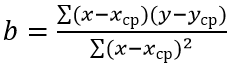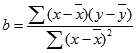Как найти угол наклона в excel

Функция НАКЛОН в Excel предназначена для определения угла наклона прямой, используемой для аппроксимации данных методом линейной регрессии, и возвращает значение коэффициента a из уравнения y=ax+b. Для определения наклона используются две любые точки на прямой. При этом вычисляется частное от деления длины отрезка, полученного при проецировании этих двух точек на ось Ординат (OY), на длину отрезка, образованного проекциями этих же двух точек на ось Абсцисс (OX).

Фактически, функция НАКЛОН вычисляет значение, которое характеризует скорость изменения данных вдоль линии регрессии. Зная наклон (коэффициент a) и значение коэффициента b можно рассчитать приближенные будущие значения какого-либо свойства y, которое меняется при изменении характеристики x.

Примеры использования функции НАКЛОН в Excel

Для расчета наклона линии регрессии используется уравнение:

где:

• x_ср – среднее значение для диапазона известных значений независимой переменной;
• y_ср – среднее значение для диапазона известных значений зависимой переменной.

Функция НАКЛОН не может быть использована для анализа коллинеарных данных и будет возвращать код ошибки #ДЕЛ/0! в отличие от функции ЛИНЕЙН, которая использует иной алгоритм расчета и возвращает как минимум одно полученное значение.

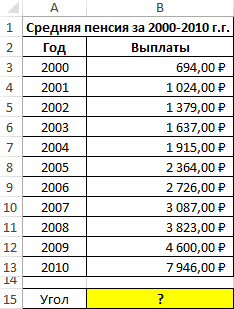
Пример 1. Определить наклон аппроксимирующей прямой для показателей средней пенсии на протяжении нескольких лет.

Вид исходной таблицы данных:

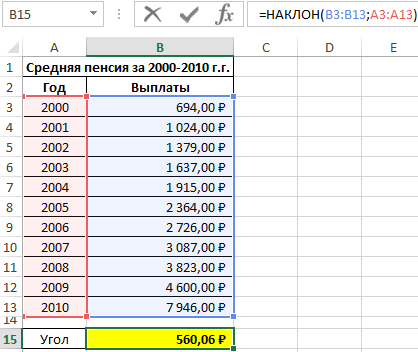
Для нахождения наклона используем следующую формулу:

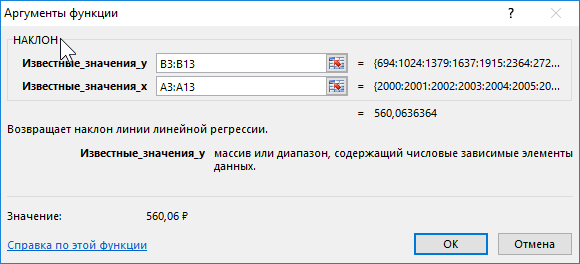
Описание аргументов:

• B3:B13 – ссылка на диапазон ячеек, содержащих данные о средней пенсии, характеризующие зависимую переменную y;
• A3:A13 – диапазон ячеек с данными об отчетных периодах (годах), характеризующие независимую переменную x.

В результате вычислений получим:

Полученное значение свидетельствует о том, что на протяжении обозначенного периода размер пенсионных выплат в среднем увеличивался примерно на 560 рублей.



Прогноз объема продаж по линейно регрессии в Excel

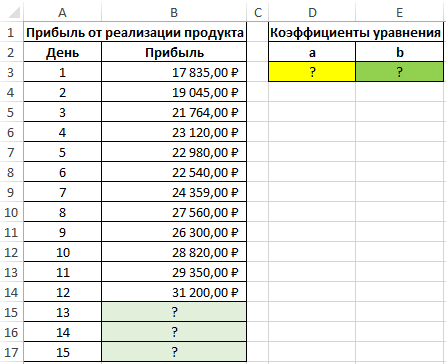
Пример 2. В таблице Excel содержатся данные о прибыли за продажи некоторого продукта компании на протяжении последних нескольких дней. Рассчитать коэффициенты a и b уравнения прямой y=ax+b, аппроксимирующей данные. На основе полученного уравнения спрогнозировать данные о продажах для трех последующих дней.

Вид таблицы с данными:

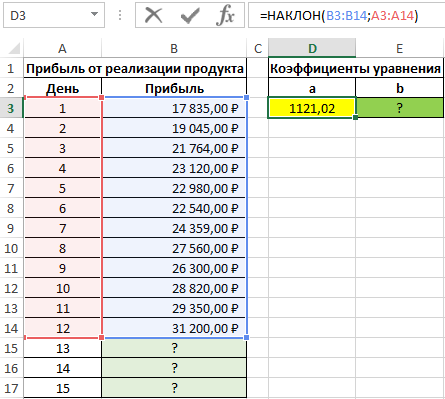
Для нахождения коэффициента a используем следующую формулу:

=НАКЛОН(B3:B14;A3:A14)

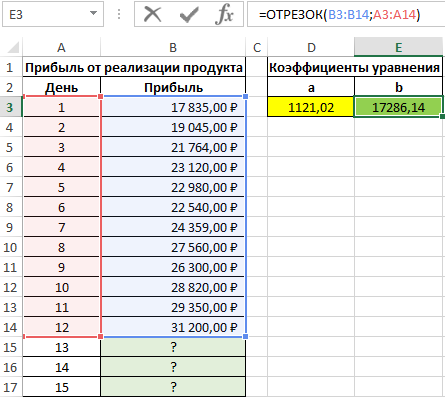
Коэффициент b рассчитывается с помощью следующей функции:

=ОТРЕЗОК(B3:B14;A3:A14)

Искомое уравнение имеет вид:

y=1121,02x+17286,14

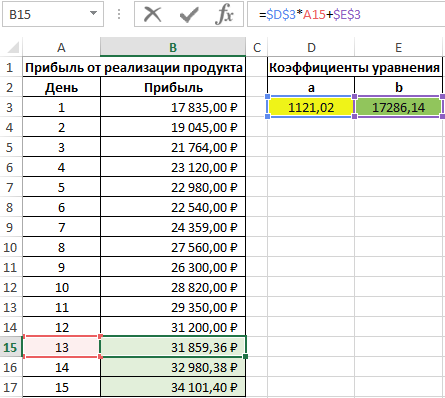
Для определения последующих значений y достаточно лишь подставить требуемое значение x. Выполним расчет предполагаемой прибыли для 13-го дня:

=$D$3*A15+$E$3

Описание аргументов:

• D3 – полученное значение коэффициента a;
• A15 – новое значение x;
• E3 – значение коэффициента b.

Используем функцию автозаполнения чтобы получить значения для остальных дней:

Анализ корреляции спроса и объема производства в Excel

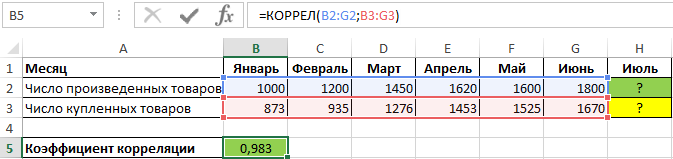
Пример 3. В таблице содержатся данные о количестве произведенной продукции за месяц, а также о числе приобретенных товаров данной марки покупателями. Отобразить взаимосвязь между данными графически, определить, целесообразно ли использовать уравнение линейно регрессии для описания корреляции между спросом и числом произведенных товаров.

Вид таблицы данных:

Для определения зависимости между двумя рядами числовых данных рассчитаем коэффициент корреляции по формуле:

=КОРРЕЛ(B2:G2;B3:G3)

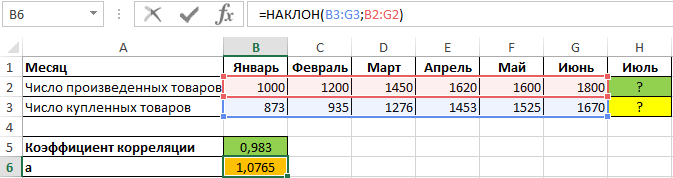
Полученное значение (0,983) свидетельствует о том, что между двумя числовыми диапазонами существует сильная прямая взаимосвязь. Поэтому целесообразно использовать аппроксимирующую прямую, для нахождения коэффициентов уравнения которой используем формулы:

=НАКЛОН(B3:G3;B2:G2)

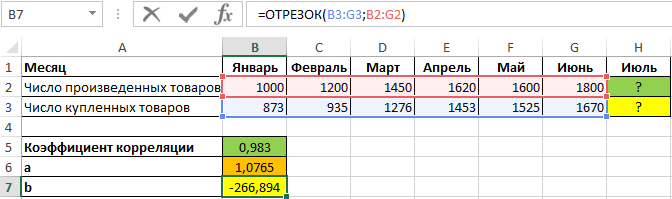
=ОТРЕЗОК(B3:G3;B2:G2)

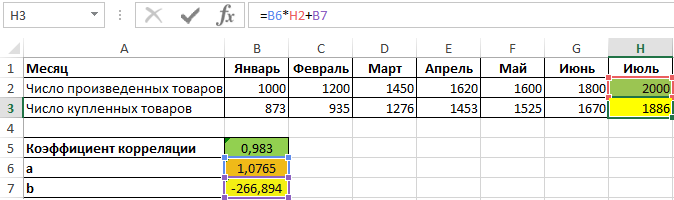
Для нахождения спроса на товары за июль при условии, что будет произведено, например, 2000 единиц продукции, используем полученное уравнение:

=B6*H2+B7

Полученное значение:

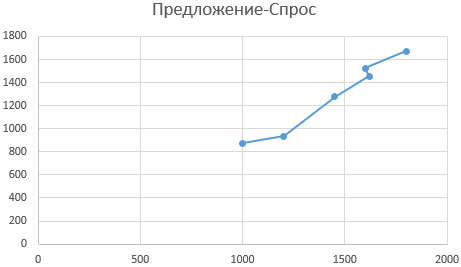
Альтернативным использованию функции НАКЛОН вариантом нахождения наклона в Excel является графический метод. Построим график на основе имеющихся данных, при этом для значений X выберем диапазон ячеек со значениями числа произведенных товаров, а для Y – с числом купленных товаров:

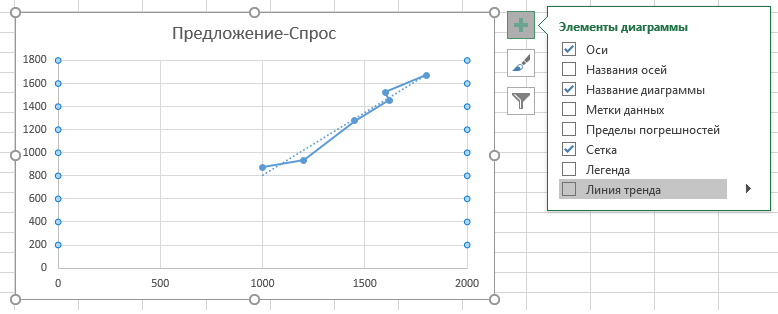
Отобразим на графике линию тренда:

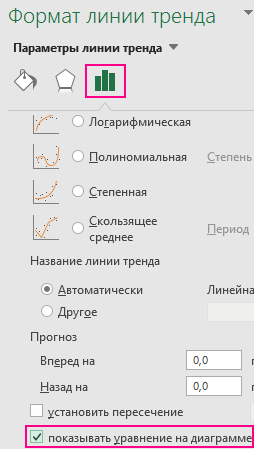
В меню «Формат линии тренда» установим флажок напротив пункта «показывать уравнение на диаграмме»:

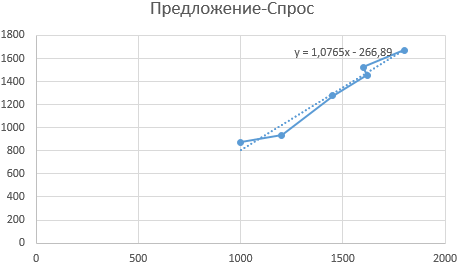
График примет следующий вид:

Как видно, найденные коэффициенты a и b соответствуют отображаемым на графике.

Особенности использования функции НАКЛОН в Excel

Функция имеет следующий синтаксис:

=НАКЛОН(известные_значения_y;известные_значения_x)

Описание аргументов (все являются обязательными для заполнения):

• известные_значения_y – аргумент, принимающий массив числовых значений или ссылку на диапазон ячеек, которые содержат числа, характеризующие значения зависимой переменной y, которые определены для известных значений x;
• известные_значения_x – аргумент, который может быть указан в виде массива чисел или ссылки на диапазон ячеек, содержащих числовые значения, которые характеризуют известные значения независимой переменной x.

Примечания:

1. В качестве аргументов должны быть переданы массивы чисел либо ссылки на диапазоны ячеек с числовыми значениями или текстовыми строками, которые могут быть преобразованы к числам. Строки, не являющиеся текстовыми представлениями числовых данных, а также логические ИСТИНА и ЛОЖЬ в расчете не учитываются.
2. Если в качестве аргументов были переданы массивы, содержащие разное количество элементов, или ссылки на диапазоны с разным количеством ячеек, функция НАКЛОН вернет код ошибки #Н/Д. Аналогичный код ошибки будет возвращен в случае, если оба аргумента принимают пустые массивы или ссылки на диапазоны пустых ячеек.
3. Если оба аргумента ссылаются на нечисловые данные, функция НАКЛОН вернет код ошибки #ДЕЛ/0!.
4. Если в диапазоне, переданном в качестве любого из аргументов, содержатся пустые ячейки, они игнорируются в расчете. Однако ячейки, содержащие значение 0 (нуль) будут учтены.

В этой статье описаны синтаксис формулы и использование функции НАКЛОН в Microsoft Excel.

Описание

Возвращает наклон линии линейной регрессии для точек данных в аргументах известные_значения_y и известные_значения_x. Наклон определяется как частное от деления расстояния по вертикали на расстояние по горизонтали между двумя любыми точками прямой; иными словами, наклон — это скорость изменения значений вдоль прямой.

Синтаксис

НАКЛОН(известные_значения_y;известные_значения_x)

Аргументы функции НАКЛОН описаны ниже.

• Известные_значения_y    Обязательный. Массив или диапазон ячеек, содержащих зависимые числовые точки данных.

• Известные_значения_x    Обязательный. Множество независимых точек данных.

Замечания

• Аргументы могут быть либо числами, либо содержащими числа именами, массивами или ссылками.

• Если аргумент, который является массивом или ссылкой, содержит текст, логические значения или пустые ячейки, эти значения игнорируются; ячейки, содержащие нулевые значения, учитываются.

• Если аргументы известные_значения_y и известные_значения_x пусты или количество содержащихся в них точек не совпадает, функция НАКЛОН возвращает значение ошибки #Н/Д.

• Уравнение наклона линии регрессии имеет следующий вид:

  

  где x и y — выборочные средние значения СРЗНАЧ(массив1) и СРЗНАЧ(массив2).

• Основной алгоритм, используемый в функциях НАКЛОН и ОТРЕЗОК, отличается от основного алгоритма функции ЛИНЕЙН. Разница между алгоритмами может привести к различным результатам при неопределенных и коллинеарных данных. Например, если точки данных аргумента известные_значения_y равны 0, а точки данных аргумента известные_значения_x равны 1, то справедливо указанное ниже.

  • Наклон и ОТОКП возвращают #DIV/0! ошибку «#ВЫЧИС!». Алгоритм НАКЛОН и ОТОКП предназначен для поиска одного и только одного ответа, и в этом случае может быть несколько ответов.

  • Функция ЛИНЕЙН возвращает значение, равное 0. Алгоритм, используемый в функции ЛИНЕЙН, предназначен для возврата правдоподобных результатов для коллинеарных данных, а в этом случае может быть найдено по меньшей мере одно решение.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Данные
Известные значения y	Известные значения x
02.01.1900	6
03.01.1900	5
09.01.1900	11
01.01.1900	7
08.01.1900	5
07.01.1900	4
05.01.1900	4
Формула	Описание	Результат
=НАКЛОН(A3:A9;B3:B9)	Наклон линии линейной регрессии для точек данных в диапазонах A3:A9 и B3:B9.	0,305556

In this article, we will look into how to calculate the slope of a line in an Excel graph.

Slope of a line basically determines two parameters :

1. The direction of a line.
2.  The steepness of a line (rise or fall).

It is generally denoted by the letter “m”. The equation of a line is given by the expression :

Where,

• m: Slope
• c: Intercept

The mathematical formula for the slope of a line is given by the ratio of rise and run and in geometry, it is denoted using tan theta.

In this article we are going to discuss various methods on how to find the slope of a line in Excel using a few examples.

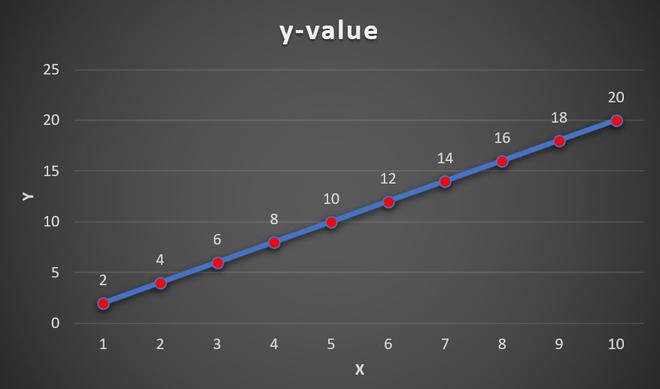
Example 1 : Consider the dataset having x and y coordinates of a particle moving in 2-D plane.

Finding Slope:

There are three methods :

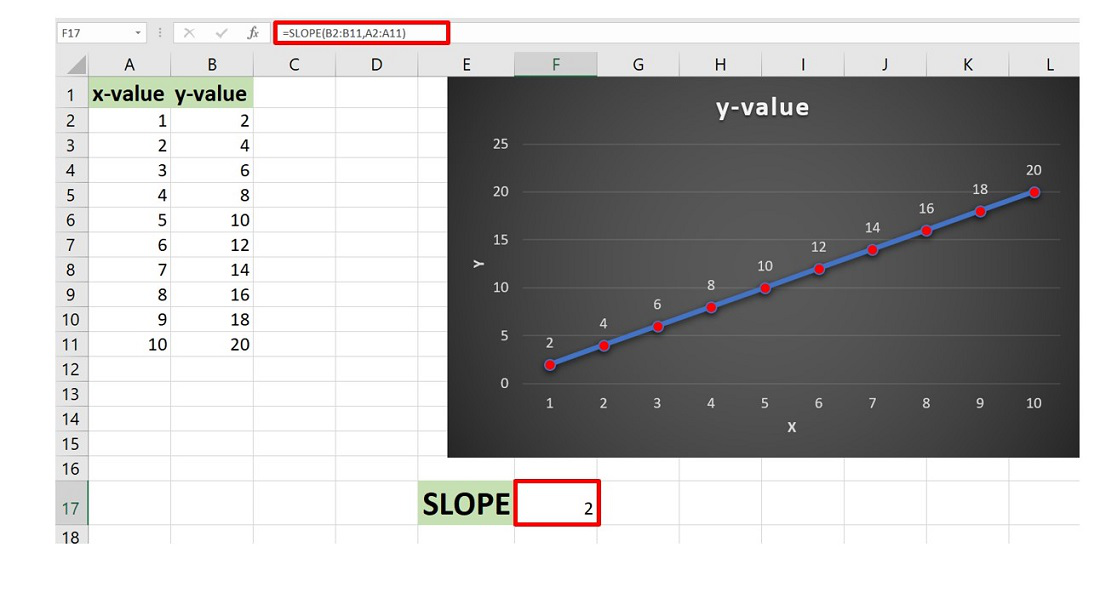
1. By using the Excel in-built function SLOPE. The syntax is :

=SLOPE(known_ys,knownx_s)

known_ys : An array of numeric data points which are dependent. These are dependent on value of horizontal axis.
known_xs : An array of numeric data points which are independent.

2. By using the slope formula as discussed. 

The steps are :

• From the data set take any pair of points.
• The points are (x1, y1) and (x2, y2).
• Use the formula and “-“,”/” operators to find the slope, m.

3. By plotting a trendline on the line graph and find its equation. From the equation of the trendline we can easily get the slope.

Method 1: Using Slope function

Here, Y-axis array is stored in B column. The array ranges from B2 to B11.

The X-axis array is stored in A column of the Excel sheet. The array ranges from A2 to A11.

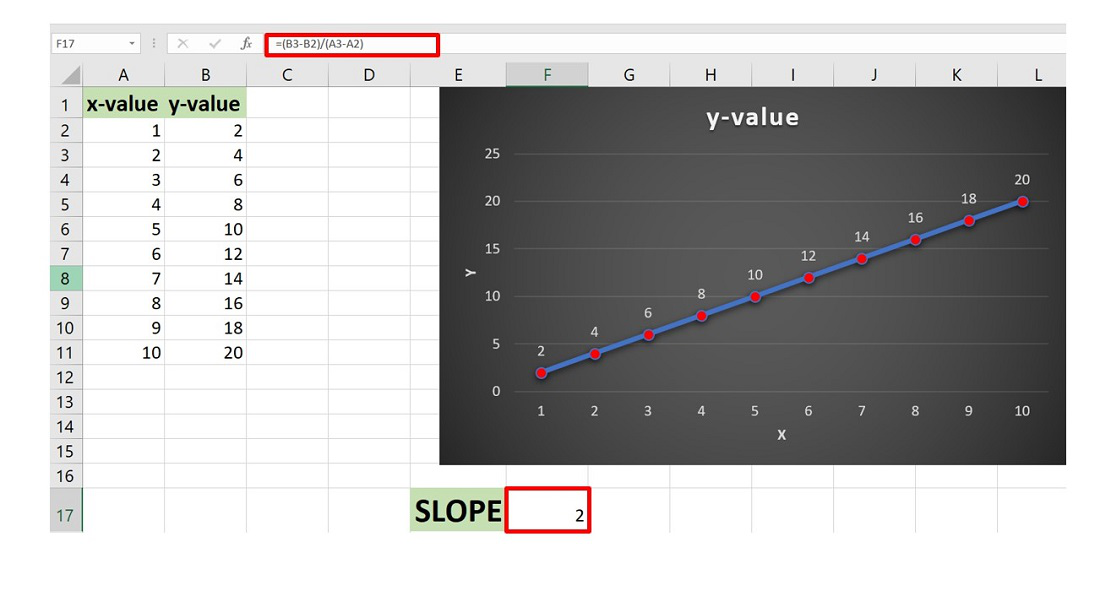
Method 2: Using Slope formula

Consider the points (1,2) and (2,4). Here, y1=2 and stored in the location B2 and y2=4 stored in location B3 and x1=1 stored in the location A2 and x2=2 stored in the location A3 of the worksheet.

Method 3:

The steps are :

• Plot the line graph by selecting the dataset and then go to the Insert Tab and then click on Insert Line or Area Chart.
• The line chart is plotted.
• Now select the chart and then click on the “+” button in the top right corner of the Chart.
• The Chart Elements dialog box appears. In this check the Trendline option. This will add the trendline to the existing line graph.

• Now select the Trendline in the chart and right-click on it and then click on Format Trendline.

• The Format Trendline dialog box opens. By default, the trendline will be linear.
• Now, check the box “Display Equation on the chart”.

• This will add the equation of the line on the chart.

The equation of the line is 

y=2x

By comparing with the general equation y = mx + c, we get

m=2, c=0

The slope is 2 for the given line.

Example 2: Consider the dataset shown below :

Similarly, by using the trendline and its equation you can easily find the slope of the line is -0.5.

Last Updated :
18 Jul, 2021

Like Article

Save Article

---

Часто вам может понадобиться найти наклон линии тренда в Excel.

К счастью, это довольно легко сделать, и следующий пошаговый пример показывает, как это сделать.

Шаг 1: Создайте данные

Во-первых, давайте создадим поддельный набор данных для работы:

Шаг 2: Создайте диаграмму рассеяния

Далее давайте создадим диаграмму рассеяния для визуализации данных.

Для этого выделите данные:

Затем щелкните вкладку « Вставка » на верхней ленте и выберите первый параметр в параметре « Вставить точечный» (X, Y) в группе « Диаграммы ». Это даст следующую диаграмму рассеяния:

Шаг 3: Добавьте линию тренда

Далее добавим линию тренда на диаграмму рассеяния.

Для этого щелкните в любом месте диаграммы рассеяния. Затем щелкните зеленый значок плюса (+) в правом верхнем углу графика и установите флажок рядом с линией тренда :

Шаг 4: Отображение наклона линии тренда

Чтобы найти наклон линии тренда, щелкните стрелку вправо рядом с линией тренда и выберите « Дополнительные параметры »:

В появившемся окне в правой части экрана поставьте галочку рядом с Display Equation on chart :

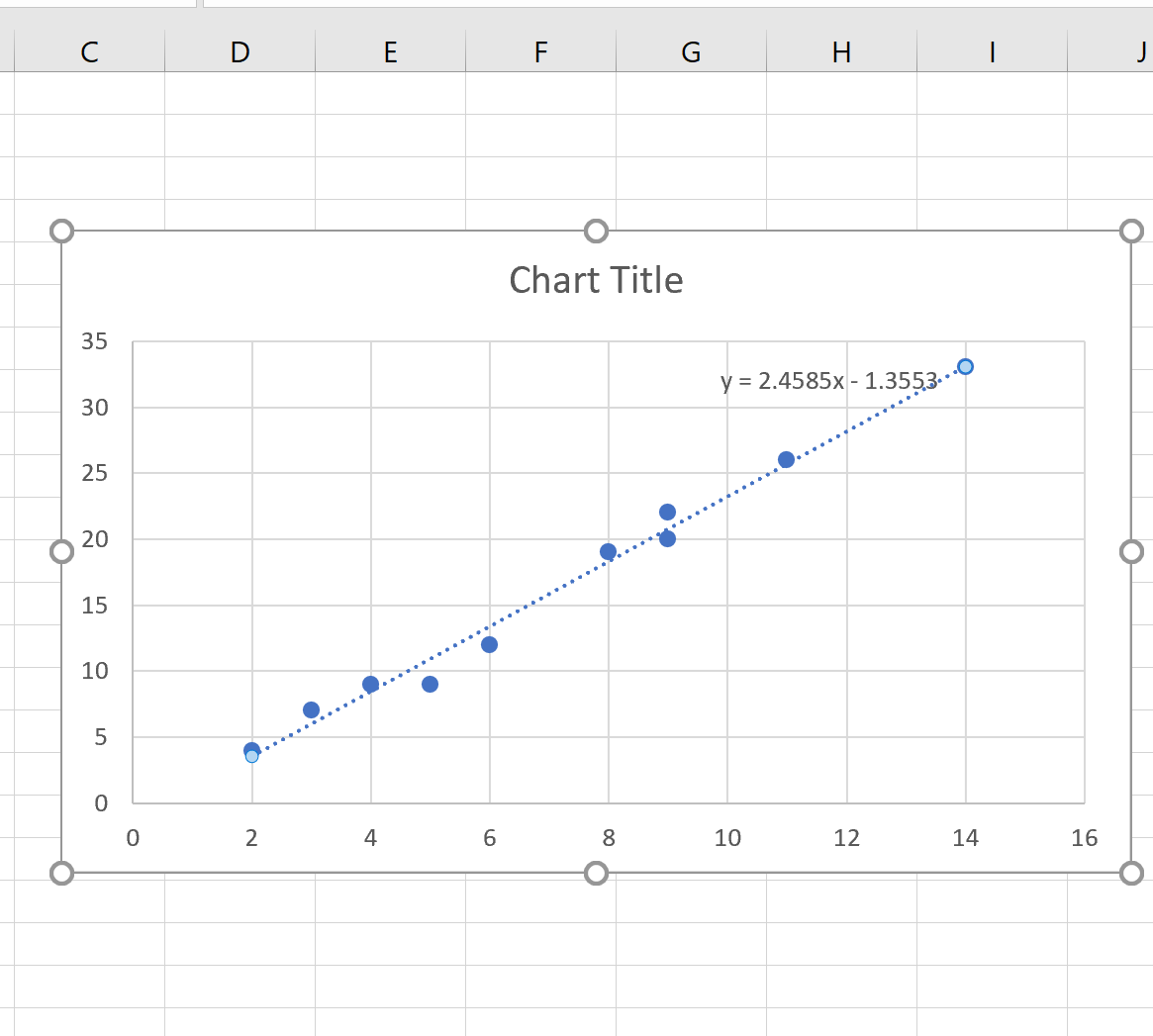
Уравнение линии тренда автоматически появится на диаграмме рассеяния:

Уравнение линии тренда оказывается y = 2,4585x – 1,3553 .

Это означает, что точка пересечения равна -1,3553 , а наклон равен 2,4585 .

---

Вы можете найти больше руководств по Excel на этой странице .