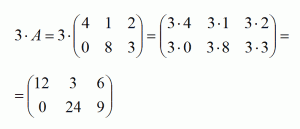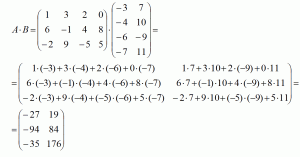Как найти угол наклона вектора к оси

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π — a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = — 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = — 1 3 0 , тогда необходимо применить формулу α = π — a r c t g k При подстановке получим выражение:

α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .

Ответ: 5 π 6 .

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , — 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , — 2 ) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · ( x — x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , — 1 ) , с угловым коэффициентом равным — 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · ( x — x 1 ) ⇔ y — ( — 1 ) = — 2 · ( x — 4 ) ⇔ y = — 2 x + 7 .

Ответ: y = — 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x — 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y — y 1 = k · ( x — x 1 ) ⇔ y — 5 = 2 · ( x — 3 ) ⇔ y = 2 x — 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3

Ответ: x 1 = y — 12 — 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = ( — 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = ( — 1 , 7 ) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .

Результат и является уравннием с угловым коэффициентом, который равняется — A B .

Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .

Ответ: y = 3 2 x — 3 .

Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x — 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x — 2 ) = 2 · ( y + 1 ) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x — 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x — 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

Координатная форма векторов

Введем понятия компоненты и проекции вектора на координатную ось Ох.

Пусть координатная ось Ох задана началом координат (точкой О), положительным направлением оси Ох и единичным масштабным отрезком. Масштаб и положительное направление оси зададим в виде единичного вектора-орта , имеющего единичную длину и направленного вдоль положительного направления координатной оси.

Из начала и конца вектора опустим на ось Ох перпендикуляры. Координаты хн, хк — являются координатами проекций Ах и Bx начала и конца вектора.

Определение: Компонентой (или составляющей) вектора на координатную ось Ох называется вектор: , идущий из проекции начала в проекцию конца вектора.

Определение: Проекцией (или координатой) вектора на координатную ось Ох называется число: , равное длине его компоненты , взятое со знаком «+», если направление компоненты совпадает с положительным направлением координатной оси и со знаком «-«, если направление компоненты противоположно положительному направлению координатной оси Ох.

Если известны координаты начала хн и конца хк вектора, то проекция или координата вектора определяется как разность координат конца и начала . Если известен угол наклона вектора к координатной оси Ох, то проекция вектора , где — модуль (длина) вектора, — угол наклона.

Компоненту вектора на координатную ось можно выразить через проекцию в виде: — это формула связи компоненты и проекции вектора.

Рассмотрим вектор на плоскости в прямоугольной системе координат Оху, которая задана началом координат (точкой О) и единичными векторами-ортами , определяющими масштаб и положительные направления координатных осей.

Взаимно перпендикулярные (ортогональные) единичные векторы-орты образуют прямоугольный базис.

Любой вектор в этой системе может быть разложен на две составляющие компоненты и представлен в виде их суммы: .

Выразим компоненты вектора через соответствующие проекции

где — единичные векторы-орты;

и — проекции вектора на оси и , которые называются координатами вектора.

Тогда вектор на плоскости можно выразить в координатной форме в виде:

где () и () -координаты начала и конца вектора. Это полная координатная форма векторов.

Можно использовать сокращенную координатную форму векторов:

Если рассматривать вектор в трехмерном пространстве, то в прямоугольной системе координат Охуz вектор раскладывается на три составляющие компоненты и представляется в виде их суммы:

Выразим компоненты через координаты вектора:

где — единичные векторы-орты, определяющие масштаб и положительные направления координатных осей,и ;

, , — проекции или координаты вектора.

Получим координатную форму вектора в трехмерном пространстве:

Можно также использовать сокращенную координатную форму вектора:

Далее для простоты и удобства построения в линейных операциях будем рассматривать векторы на плоскости. При переходе к трехмерному пространству добавляется лишь третья координата вектора.

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.

Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Произведение вектора на число:

Скалярное произведение векторов:

Косинус угла между векторами:

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами и . Для этого нужны их координаты.

Запишем координаты векторов:

и найдем косинус угла между векторами и :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

Из прямоугольного треугольника AOS найдем

Координаты вершины пирамиды:

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

Найдем координаты векторов и

и угол между ними:

Покажем теперь, как вписать систему координат в треугольную призму:

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

Найдем координаты векторов и , а затем угол между ними:

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

То есть A + C + D = 0.

Аналогично для точки K:

Получили систему из трех уравнений:

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

Выразим C и B через A и подставим в третье уравнение:

Решив систему, получим:

Уравнение плоскости MNK имеет вид:

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку имеет вид:

Угол между плоскостями равен углу между нормалями к этим плоскостям:

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть:

Напишем уравнение плоскости AEF.

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

Координаты вектора — тоже:

Находим угол между плоскостями, равный углу между нормалями к ним:

Зная косинус угла, находим его тангенс по формуле

Получим:

Ответ:

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

Находим координаты вектора .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

Ответ:

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Чтобы найти угол вектора с осью Ох, берут х-координату и делят на длину вектора. Полученное значение равно косинусу искомого угла. Используя функцию arccos находят угол. Аналогично действуют, чтобы найти угол вектора с осью Оу, только на длину вектора делят у-координату. Такие же вычисления производятся в случае трёхмерных векторов, а также при определении углов с осями координат векторов произвольной размерности.

Пример, пусть вектор имеет координаты (3; -4).

Длина данного вектора:

(3^2+(-4)^2)^(1/2) = 5.

Угол с осью Ох:

arccos(3/5) = 0,9273 рад = 53,13°.

Угол с осью Оу:

arccos(-4/5) = 2,5 рад = 143,13°.

Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x₁-x₂) никак не разделить и т.д.

Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.

Коэффициенты А, B, C

Все помним со школы формулу:

Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):

Те же фаберже, только сбоку.

В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.

Загвоздка в том, что мы не знаем коэффициенты для обеих линий.

В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:

Путем несложных операций приходим к следующей записи:

Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:

Пока все идет отлично, нигде вероятного деления на ноль не встретилось.

Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.

Система уравнений

Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.

Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.

Сразу же запишем метод под нашу систему.

Имеем следующую систему:

Определители будут такими:

Исходя из метода, решение выглядит так:

Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности).  В коде, естественно, этот момент надо учитывать.

Практика 1

Частные случаи

• Прямые параллельны: ∆_ab = 0
  • (A₁B₂ – B₁A₂ = 0);
• Прямые совпадают:  ∆_ab = ∆_X = ∆_Y = 0 
  • (A₁B₂ – B₁A₂ = 0) И (A₁C₂ — A₂C₁ = 0) И (C₁B₂ -B₁C₂ = 0);
• Прямые перпендикулярны:
  • (A₁ A₂ + B₁ B₂ = 0).

Принадлежность точки отрезку

В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:

1. Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
2. Проверить факт нахождения точки между концами отрезка.

Займемся пунктом 2. Данный факт можно установить двумя способами:

• Логически, т.е. (x₁ <= x <= x₂) ИЛИ (x₁ >= x >= x₂). На случай «вертикальности» линии добавить проверку на Y:
  • (y₁ <= y <= y₂) ИЛИ (y₁ >= y >= y₂).
• Арифметически. Сумма отрезков |x-x₁| + |x-x₂| должна быть равна длине отрезка |x₁-x₂|. Аналогично, на случай «вертикальности» , добавить проверку:
  • |y-y₁| + |y-y₂| = |y₁-y₂|

Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.

Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.

Угол пересечения прямых

Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p₁ и p₂, получим направляющий вектор V(p₁,p₂), и аналогично второй вектор M(p₃,p₄). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.

Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:

α — угол наклона вектора к оси X, который можно найти, как:

α = arctan (A₁ / B₁)

Где расстояния:

A₁ = (y₁ — y₂)

B₁ = (x₂ — x₁)

Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…

Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.

Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.

По рисунку явно видно, что угол между векторам это γ = (β — α).

В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.

От теории к практике

Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.

Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.

Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:

Тут ситуация с вертикальной прямой, т.е. когда теоретически происходит деление на ноль, явно не обрабатывается. Она корректно обрабатывается функцией ArcTan2, которая вернет в этом случае и знак, и 90 градусов.  

Практика 2

В дополнение к функции нахождения точки пересечения, напишем «продвинутую» функцию, которая находит эту точку, определяет нахождение на каждом из отрезков, и определяет угол между направляющими векторами. Или же определяет, что прямые параллельны/совпадают.

Исходники

Небольшие комментарии по интерфейсу.

Скачать (219 Кб): Исходники (Delphi XE 7-10)

Скачать (1.14 Мб): Исполняемый файл

При запуске генерируется случайным образом 4 точки, по две на прямую. Точки и отрезки можно перетаскивать мышкой. Также, слева присутствует панель, на которой можно ввести координаты точек или коэффициенты уравнения прямой. При нажатии «Enter» или когда элемент ввода теряет фокус, происходит перерасчет и перерисовка.

Внизу есть 4 кнопки переключения режимов отображения. Начиная со второй, помимо координат точки пересечений в верхнем левом углу будет отображаться текущий угол пересечения между направляющими векторами.

Если точка пересечений попадает в какой-либо из отрезков, соответствующий заголовок линии отрезка станет жирным. На рисунке это зеленая линия 2.

По умолчанию, рабочее поле системы координат имеет размерность [-10..10], которую можно изменить ползунком в нижнем правом углу.

1.Определителем
второго порядка
называется число равное разности
произведений элементов главной и второй
диагонали: Определителем
третьего порядка называется следующее
выражение: 

Определитель
третьего порядка вычислить
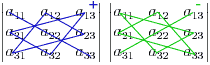
легко, если учесть следующее правило:
со знаком плюс идут произведения троек
чисел, расположенных на главной диагонали
матрицы, и в вершинах треугольников с
основанием параллельным этой диагонали
и вершиной в противоположого угла
матрицы. Со знаком минус идут тройки из
второй диагонали и из треугольноков,
построенных относительно этой диагонали.
Следующая схема демонстрирует это
правило, называемое правилом треугольников.
В схеме синим (слева) отмечены элементы,
чьи произведения идут со знаком плюс,
а зеленым (справа) — со знаком минус. 

Свойство
1.
Определитель не меняется при
транспонировании.
Это означает, что определитель матрицы
равен определителю транспонированной
матрицы (матрицы, в которой строки
заменены соответствующими столбцами).

Исходя
из первого свойства, в остальных свойствах
мы можем говорить только о строках,
подразумевая, что эти свойства применими
также и к столбцам.

Свойство
2.
Если одна из строк определителя состоит
из нулей, то определитель равен нулю.

Свойство
3.
От перестановки двух строк определитель
меняет свой знак.

Свойство
4.
Определитель, содержащий две одинаковые
строки, равен нулю.

Свойство
5.
Если все элементы некоторой строки
умножить на некое число, то сам определитель
умножится на это число.

Свойство
6.
Определитель, содержащий две
пропорциональные строки, равен нулю.

Свойство
7.
Если все элементы i-й строки определителя
n-го порядка представлен в виде суммы
двух слагаемых: a_ij=b_j+c_j,
j = 1, …, n, то определитель
равен сумме двух определителей, у которых
все строки, кроме i-й, — такие же, как и в
заданом определителе, а i-я строка в
одном из слагаемых состоит из элементов
b_j,
в другом — из элементов c_j.

Свойство
8.
Если одна из строк определителя есть
линейная комбинация его других строк,
то определитеь равен нулю..

Свойство
9.
Определитель не меняется, если к одной
из его строк прибавляется любая линейная
комбинация других строк.

2.
Алгебраическим
дополнением элемента  матрицы  называется
число

,где  — дополнительный
минор, определитель матрицы,
получающейся из исходной матрицы  путем
вычёркивания i -й
строки и j -го
столбца..Минор  матрицы A ― определитель квадратной
матрицы порядка k (который
называется также порядком этого минора),
элементы которой стоят в матрице A на
пересечении строк с номерами  и
столбцов с номерами 

3.
Метод Крамера (правило Крамера) —
способ решения квадратных систем
линейных алгебраических уравнений с
ненулевым определителем основной
матрицы (причём
для таких уравнений решение существует
и единственно)
Определители:
Решение:

4.
Сумма
двух матриц: Разность двух матриц
Умножение на число.

:

Найдем
произведение этих матриц:

5.
^{Обра́тная
ма́трица —
такая матрица A−1,
при умножении на которую исходная
матрица A даёт
в результате единичную
матрицу E:}

матричным уравнением.

5)
Обра́тная ма́трица —
такая матрица A⁻¹,
при умножении на которую исходная
матрица A даёт
в результате единичную
матрицу E:

. Матричная
запись системы линейных уравнений 
AX
= B,гдеМатрицу A называют
матрицей (или основной матрицей) системы.
Матрицуназывают
расширенной матрицей системы, а
матрицу  для
которой AС
= В,
— вектор-решением системы.6)тоже
самое)

7)
Это пространство называется
трёхмерным, так оно имеет три
однородных измерения — высоту, ширину и длину,
то есть трёхмерное пространство
описывается тремя
единичными ортогональными векторами..(
направленный отрезок, то есть отрезок,
у которого указаны начало, называемое
также точкой приложения В. и конец)

Линейные
операции: сложение
векторовПусть
даны два вектора  и .
Приложим вектор  к
точке  (концу
вектора )
и получим вектор  (рис.1.7,а;
здесь и далее равные векторы отмечены
одинаковыми засечками).
Вектор  называется суммой
векторов  и  и
обозначается .
Это нахождение суммы называется правилом
треугольника Вычитание векторов
:
Разностью векторов  и  называется
сумма вектора  с
вектором ,
противоположным вектору :
Умножение
векторов
Произведением ненулевого вектора а на
действительное число  называется
вектор ,
удовлетворяющий условиям:1)
длина вектора  равна ,
т.е. 2)
векторы  и  коллинеарные ;3)
векторы  и  одинаково
направлены, если ,
и противоположно направлены, если .

Набор
векторов  называется системой
векторов.Система
из  векторов  называется линейно
зависимой,
если существуют такие числа ,
не все равные нулю одновременно, что
Система
из  векторов  называется линейно
независимой, если
равенство (1.1) возможно только при ,
т.е. когда линейная комбинация в левой
части (1.1) тривиальная.

9)
Пусть  –
произвольный вектор,  –
произвольная система векторов.
Если выполняется равенство

,
(1)то говорят, что вектор  представлен
в виде линейной комбинации
данной системы векторов.
Если данная система векторов  является
базисом векторного пространства,
то равенство (1)
называется разложением вектора  по
базису . Коэффициенты
линейной комбинации  называются
в этом случае координатами
вектора  относительно
базиса ..(Теорема.
(О разложении вектора по базису.)Любой
вектор векторного пространства можно
разложить по его базису и притом
единственным способом)

10)Проекцией
вектора  на
ось  называется
разность проекций конца вектора и его
начала.
Проекция на ось суммы векторов равна
сумме их проекций. Проекция на ось суммы
векто
Проекцией вектора b на
вектор a,  ,
будем называть проекцию вектора b на
любую ось, параллельную вектору a и
имеющую направление, совпадающее с
направлением вектора a.
        Проекция
вектора b на
вектор a обозначается  .Очевидно,
что  ,
где   —
угол между векторами a и b.

ров
равна сумме их проекций.

Проекцией
вектора на ось u называется число, равное
величине отрезка оси u, где точка
является проекцией точки А на ось u, а
— проекцией точки В на эту ось.

Проекция
вектора на ось u обозначается символом
. Если вектор обозначен символом , то
его проекцию на ось u принято обозначать:
.

Проекция
вектора на ось u выражается через его
модуль и угол наклона к оси u формулой

Проекции
произвольного вектора на оси некоторой
заданной системы координат в дальнейшем
обозначаются буквами X, Y, Z. Равенство
={X, Y, Z} означает, что числа X, Y, Z являются
проекциями вектора на координатные
оси. Вектор, для которого X=Y=Z=0, называется
нулевым и обозначается Проекции вектора
на координатные оси называются также
его (декартовыми) координатами. Если
даны две точки (, , ) и (, , ), являющиеся
соответственно началом и концом вектора
, то его координаты X, Y, Z определяются
по формулам , , .

11.Скалярное произведение векторов. Его свойства.

Скалярное
произведение векторов. __ __

Угол
между ненулевыми векторами AB и CD – это
угол, образованный векторами при их
параллельном переносе до совмещения
точек A и C. Скалярным произведением
векторов a и b называется число, равное
произведению их длин на косинус угла
между ними:

Если
один из векторов нулевой, то их скалярное
произведение в соответствии с определением
равно нулю:

(
a , 0 ) = ( 0 , b ) = 0 .

Если
оба вектора ненулевые, то косинус угла
между ними вычисляется по формуле:

Скалярное
произведение ( a , a ), равное | a | 2, называется
скалярным квадратом. Длина вектора a
и его скалярный квадрат связаны
соотношением

Скалярное
произведение двух векторов:

—
положительно, если угол между векторами
острый ;

—
отрицательно, если угол между векторами
тупой .

Скалярное
произведение двух ненулевых векторов
равно нулю тогда и только тогда, когда
угол между ними прямой, т.е. когда эти
векторы перпендикулярны (ортогональны):

Свойства
скалярного произведения. Для любых
векторов a , b , c и любого числа m справедливы
следующие соотношения:

I.
( a , b ) = ( b , a ) . ( П е р е м е с т и т е
л ь н ы й закон )

II.
( m a , b ) = m ( a , b ) .

III.
( a + b , c ) = ( a , c ) + ( b , c ). (
Р а с п р е д е л и т е л ь н ы й закон )

Единичные
ортогональные векторы. В любой
прямоугольной системе координат можно
ввести единичные попарно ортогональные
векторы i, j и k, связанные с координатными
осями: i – с осью Х, j – с осью Y и k – с
осью Z. В соответствии с этим определением:

(
i , j ) = ( i , k ) = ( j , k ) = 0,

|
i | = | j | = | k | = 1.

Любой
вектор a может быть выражен через эти
векторы единственным образом: a = x i + y
j + z k . Другая форма записи: a = ( x, y, z ).
Здесь x, y, z — координаты вектора a в
этой системе координат. В соответствии
с последним соотношением и свойствами
единичных ортогональных векторов i,
j , k скалярное произведение двух векторов
можно выразить иначе.

Пусть
a = ( x, y, z ); b = ( u, v, w ). Тогда
( a , b ) = xu + yv + zw.

Скалярное
произведение двух векторов равно сумме
произведений соответствующих координат.

Длина
(модуль) вектора a = ( x, y, z )

Кроме
того, теперь мы получаем возможность
проведения алгебраических операций
над векторами, а именно, сложение и
вычитание векторов можетвыполняться
по координатам:

a
+ b = ( x + u , y + v , z + w ) ;

a
– b = ( x – u , y – v , z – w ) .

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Here a little program in Python that uses the angle between vectors to determine if a point is inside or outside a certain polygon

import sys
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
from shapely.geometry import Point, Polygon
from pprint import pprint

# Plot variables
x_min, x_max = -6, 12
y_min, y_max = -3, 8
tick_interval = 1
FIG_SIZE = (10, 10)
DELTA_ERROR = 0.00001
IN_BOX_COLOR = 'yellow'
OUT_BOX_COLOR = 'black'


def angle_between(v1, v2):
    """ Returns the angle in radians between vectors 'v1' and 'v2'
        The sign of the angle is dependent on the order of v1 and v2
        so acos(norm(dot(v1, v2))) does not work and atan2 has to be used, see:
        https://stackoverflow.com/questions/21483999/using-atan2-to-find-angle-between-two-vectors
    """
    arg1 = np.cross(v1, v2)
    arg2 = np.dot(v1, v2)
    angle = np.arctan2(arg1, arg2)
    return angle


def point_inside(point, border):
    """ Returns True if point is inside border polygon and False if not
        Arguments:
        :point: x, y in shapely.geometry.Point type
        :border: [x1 y1, x2 y2, ... , xn yn] in shapely.geomettry.Polygon type
    """    
    assert len(border.exterior.coords) > 2,
        'number of points in the polygon must be > 2'

    point = np.array(point)
    side1 = np.array(border.exterior.coords[0]) - point
    sum_angles = 0
    for border_point in border.exterior.coords[1:]:
        side2 = np.array(border_point) - point
        angle = angle_between(side1, side2)
        sum_angles += angle
        side1 = side2

    # if wn is 1 then the point is inside
    wn = sum_angles / 2 / np.pi
    if abs(wn - 1) < DELTA_ERROR:
        return True
    else:
        return False


class MainMap():

    @classmethod
    def settings(cls, fig_size):
        # set the plot outline, including axes going through the origin
        cls.fig, cls.ax = plt.subplots(figsize=fig_size)
        cls.ax.set_xlim(-x_min, x_max)
        cls.ax.set_ylim(-y_min, y_max)
        cls.ax.set_aspect(1)
        tick_range_x = np.arange(round(x_min + (10*(x_max - x_min) % tick_interval)/10, 1),
            x_max + 0.1, step=tick_interval)
        tick_range_y = np.arange(round(y_min + (10*(y_max - y_min) % tick_interval)/10, 1), 
            y_max + 0.1, step=tick_interval)
        cls.ax.set_xticks(tick_range_x)
        cls.ax.set_yticks(tick_range_y)
        cls.ax.tick_params(axis='both', which='major', labelsize=6)
        cls.ax.spines['left'].set_position('zero')
        cls.ax.spines['right'].set_color('none')
        cls.ax.spines['bottom'].set_position('zero')
        cls.ax.spines['top'].set_color('none')

    @classmethod
    def get_ax(cls):
        return cls.ax

    @staticmethod
    def plot():
        plt.tight_layout()
        plt.show()


class PlotPointandRectangle(MainMap):

    def __init__(self, start_point, rectangle_polygon, tolerance=0):

        self.current_object = None
        self.currently_dragging = False
        self.fig.canvas.mpl_connect('key_press_event', self.on_key)
        self.plot_types = ['o', 'o-']
        self.plot_type = 1
        self.rectangle = rectangle_polygon

        # define a point that can be moved around
        self.point = patches.Circle((start_point.x, start_point.y), 0.10,
            alpha=1)
        if point_inside(start_point, self.rectangle):
            _color = IN_BOX_COLOR
        else:
            _color = OUT_BOX_COLOR
        self.point.set_color(_color)
        self.ax.add_patch(self.point)
        self.point.set_picker(tolerance)
        cv_point = self.point.figure.canvas
        cv_point.mpl_connect('button_release_event', self.on_release)
        cv_point.mpl_connect('pick_event', self.on_pick)
        cv_point.mpl_connect('motion_notify_event', self.on_motion)

        self.plot_rectangle()

    def plot_rectangle(self):
        x = [point[0] for point in self.rectangle.exterior.coords]
        y = [point[1] for point in self.rectangle.exterior.coords]
        # y = self.rectangle.y
        self.rectangle_plot, = self.ax.plot(x, y,
            self.plot_types[self.plot_type], color='r', lw=0.4, markersize=2)

    def on_release(self, event):
        self.current_object = None
        self.currently_dragging = False

    def on_pick(self, event):
        self.currently_dragging = True
        self.current_object = event.artist

    def on_motion(self, event):
        if not self.currently_dragging:
            return
        if self.current_object == None:
            return

        point = Point(event.xdata, event.ydata)
        self.current_object.center = point.x, point.y
        if point_inside(point, self.rectangle):
            _color = IN_BOX_COLOR
        else:
            _color = OUT_BOX_COLOR
        self.current_object.set_color(_color)

        self.point.figure.canvas.draw()

    def remove_rectangle_from_plot(self):
        try:
            self.rectangle_plot.remove()
        except ValueError:
            pass

    def on_key(self, event):
        # with 'space' toggle between just points or points connected with
        # lines
        if event.key == ' ':
            self.plot_type = (self.plot_type + 1) % 2
            self.remove_rectangle_from_plot()
            self.plot_rectangle()
            self.point.figure.canvas.draw()


def main(start_point, rectangle):

    MainMap.settings(FIG_SIZE)
    plt_me = PlotPointandRectangle(start_point, rectangle)  #pylint: disable=unused-variable
    MainMap.plot()

if __name__ == "__main__":
    try:
        start_point = Point([float(val) for val in sys.argv[1].split()])
    except IndexError:
        start_point= Point(0, 0)

    border_points = [(-2, -2),
                     (1, 1),
                     (3, -1),
                     (3, 3.5),
                     (4, 1),
                     (5, 1),
                     (4, 3.5),
                     (5, 6),
                     (3, 4),
                     (3, 5),
                     (-0.5, 1),
                     (-3, 1),
                     (-1, -0.5),
                    ]               

    border_points_polygon = Polygon(border_points)
    main(start_point, border_points_polygon)