Как найти угол наклонной плоскости формулы

Расчет угла наклона плоскости

Плоскость — это поверхность, содержащая прямые, соединяющие две любые ее точки.

Угол наклона плоскости — это угол вершины противоположный высоте плоскости.

Для расчета угла наклона плоскости используются тригонометрические формулы.

Быстро выполнить эту простую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета угла наклона плоскости, если известны основание и высота. С помощью этого калькулятора вы в один клик сможете вычислить угол наклона плоскости.

Научная электронная библиотека

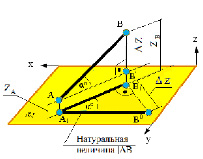
Прямая общего положения на плоскости проекций отображается с искажением (рис.4.6). Для того чтобы найти её натуральную величину, необходимо воспользоваться правилом прямоугольного треугольника, согласно которому на комплексном чертеже натуральной величиной прямой является гипотенуза прямоугольного треугольника, построенного на двух катетах. Один из этих двух катетов – это проекция рассматриваемой прямой, а вторым катетом является разность координат начала и конца этой прямой или разность координат z точек А и В (Δz = zA – zB).

Углы наклона прямой общего положения к плоскостям проекций по двум ее проекциям находят при определении действительной величины этой прямой способом прямоугольного треугольника. Если взять прямую общего положения АВ и спроецировать ее на горизонтальную плоскость проекций, а через точку А провести линию, параллельную плоскости, то в пространстве получится прямоугольный треугольник, один из катетов которого (AB’) равен длине проекции прямой АВ, а угол между прямой и этим катетом будет углом наклона заданной прямой к горизонтальной плоскости проекций (рис. 4.6), что можно подтвердить известным математическим соотношением:

Прямая А1В0 представляет натуральную величину прямой общего положения АВ.

Для определения натуральной величины прямой общего положения АВ и угла наклона её к плоскости проекций на эпюре (комплексном чертеже) необходимо построить прямоугольный треугольник:

— первый катет этого треугольника равен проекции прямой, на плоскости проекций;

— для построения второго катета необходимо из проекции любого конца проекции прямой линии под прямым углом к проекции провести луч, на котором отложить длину второго катета, равную разности расстояний от концов прямой до данной плоскости проекций;

— гипотенуза полученного прямоугольного треугольника будет равна действительной величине заданной прямой;

— угол наклона прямой линии к той или иной плоскости проекций равен углу между гипотенузой – натуральной величиной и катетом – проекцией прямой на эту плоскость проекций.

Углы наклона прямой линии общего положения к плоскости, всегда меньше их ортогональных проекций.

Рис. 4.6. Определение угла наклона и натуральной величины отрезка

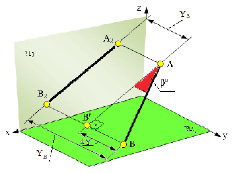
Учитывая сказанное выше и рассмотрев рис. 4.7, можно утверждать, что длина отрезка АВ равна гипотенузе треугольника, катетами которого являются фронтальная проекция отрезка А2В2 и разность координат Y точек А и В (ΔY = YB – YA). Угол этого треугольника, лежащий против катета ΔY, равен углу наклона отрезка АВ к фронтальной плоскости проекций π2 (угол β°).

По аналогии длина отрезка АВ может быть определена и как гипотенуза треугольника, катеты которого профильная проекция отрезка А3В3 и разность координат Х (Δ Х = ХА – ХВ) точек А и В. Угол γ° этого треугольника, лежащий против катета Δ Х, определяет угол наклона отрезка АВ к профильной плоскости проекций π3.

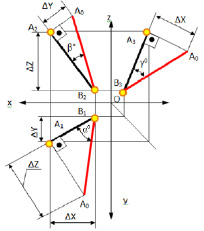
На рис. 4.8 показан пример определения натуральной (действительной) длины прямой АВ и углов её наклона к плоскостям проекций.

Рис. 4.7. Определение угла наклона и натуральной величины отрезка

Рис. 4.8. Определение длины отрезка и углов наклона к плоскостям проекций на комплексном чертеже

Угол αº, получен при построении прямоугольного треугольника на горизонтальной проекции прямой. Углы β и γ определены с использованием фронтальной и профильной проекций прямой соответственно. Натуральная величина, указанной прямой, обозначена гипотенузами прямоугольных треугольников, построенных на трёх плоскостях проекций.

Построение плоскости, проходящей через заданную прямую линию

Через произвольную прямую линию общего положения можно провести сколько угодно плоскостей общего положения. Для примера на рис. 4.25 плоскость задана двумя пересекающимися прямыми: заданной А В и произвольной А С.

Через прямую линию общего положения, например АВ, можно провести три проецирующие плоскости: горизонтально проецирующую (рис. 4.26, а), фронтально проецирующую (рис. 4.26, б) и профильно проецирующую (рис. 4.26, в).

Плоскость уровня через прямую общего положения провести невозможно.

Определение углов наклона плоскости к основным плоскостям проекций

Угол между заданной плоскостью и плоскостью проекций проецируется без искажения только в том случае, если она занимает проецирующее положение. Для плоскостей общего положения углы наклона определяют с помощью замены плоскостей проекций. При этом плоскость общего положения в новой системе должна быть перпендикулярна новой плоскости проекций.

Чтобы плоскость заняла проецирующее положение, необходимо одну из ее линий уровня спроецировать на новую плоскость проекций в виде точки. Это объясняется тем, что только проецирующие плоскости содержат проецирующие прямые.

Для определения угла наклона плоскости общего положения а (ЛВС) к горизонтальной плоскости проекций ее нужно превратить в горизонтально проецирующую, проведя горизонтальную прямую А1 (рис. 4.27) и задав новую плоскость 71₄ перпендикулярно А1, а следовательно, и к плоскости проекций щ: (тс₄± а) _1_ 711 => Х ± А ‘ 1 И а).

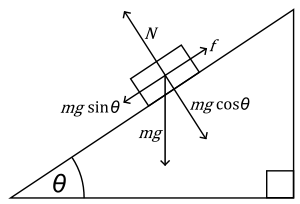
Наклонная плоскость — это плоская поверхность, установленная под углом, отличным от прямого и/или нулевого, к горизонтальной поверхности. Наклонная плоскость позволяет преодолевать значительное сопротивление, прилагая сравнительно малую силу на большем расстоянии, чем то, на которое нужно поднять груз.

Наклонная плоскость — один из широко известных простых механизмов.

Примеры наклонных плоскостей

Примерами наклонных плоскостей служат:

• пандусы и трапы;
• инструменты: стамеска, топор, молоток, плуг, клин и так далее;

Наиболее канонический пример наклонной плоскости — наклонная поверхность, например, въезд на мост с перепадом высоты.

История

Пандусы, или наклонные плоскости, широко использовались при строительстве ранних каменных сооружений, дорог и акведуков. Также они применялись при штурме военных укреплений.

Эксперименты с наклонными плоскостями помогли средневековым физикам (таким, как Галилео Галилей) изучить законы природы, связанные с гравитацией, массой, ускорением и т. д.

Глубокое понимание наклонных плоскостей и их использования помогло прийти к осознанию того, как векторные величины, такие как силы, можно успешно анализировать и управлять ими с помощью математики^{[источник не указан 1035 дней]}. Концепция суперпозиции и декомпозиции очень важна для многих областей современной науки, техники и технологии.

Формулы для наклонной плоскости

здесь  — коэффициент трения тела о поверхность,  — угол наклона плоскости.

Предельным является случай, когда угол наклона плоскости равен 90^o градусам, то есть тело падает, скользя по стене. В этом случае: , то есть сила трения никаким образом не влияет на тело, оно находится в свободном падении. Другим предельным случаем является ситуация, когда угол наклона плоскости равен нулю, т.е. плоскость параллельна земле; в этом случае тело не может двигаться без приложения внешней силы. Надо заметить, что, следуя из определения, в обеих ситуациях плоскость уже не будет являться наклонной — угол наклона не должен быть равен 90^o или 0^o.

Критический угол

Род передвижения тела зависит от критического угла. Тело покоится, если угол наклона плоскости меньше критического угла, покоится или движется равномерно, если угол наклона плоскости равен критическому углу, и движется равноускоренно, при условии что угол наклона плоскости больше критического угла.

Далее описаны все три возможные ситуации, в них:  — коэффициент трения,  — угол наклона плоскости, β — критический угол.

Можно отметить, что .

См. также

• Клин
• Коэффициент трения

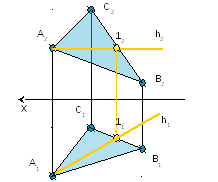
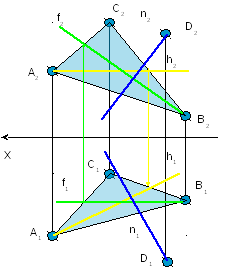
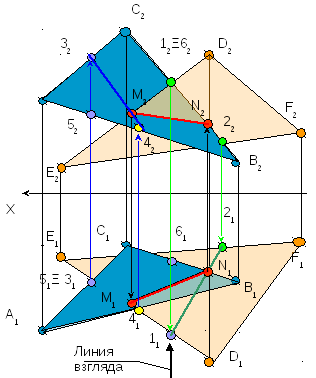
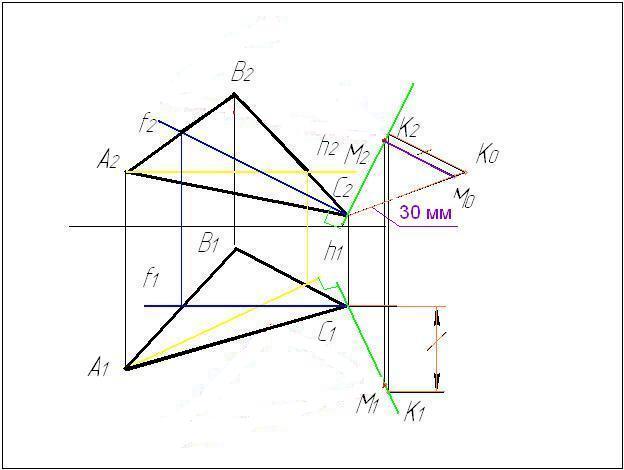
Задача № 1.

Условие задачи:

Определить
углы наклона плоскости ΔАВС к плоскостям
проекций П₁,
П₂,
П₃.Исходные
данные к задаче представлены в таблице
1.

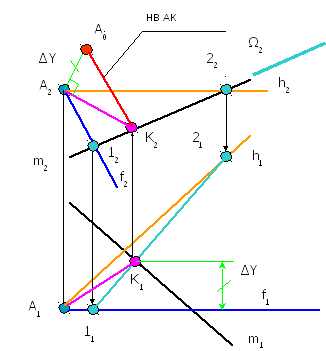
Рисунок 1

Решение:

Задачу рассмотрим
на примере нахождения угла наклона
плоскости ΔАВС к плоскостям проекций
П₁.

Алгоритм решения
задачи следующий:

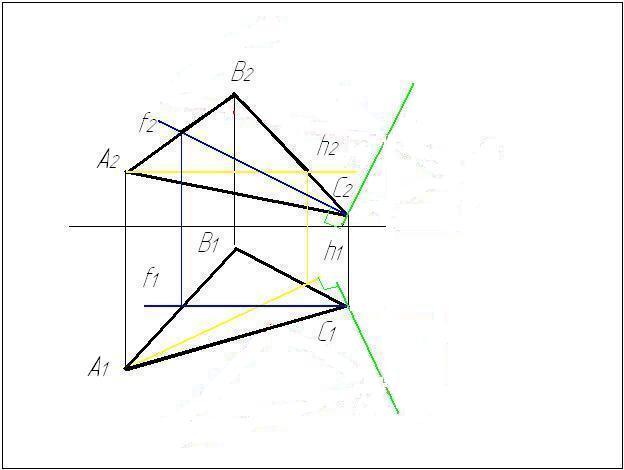
1 Проводим главную
линию плоскости (линию уровня), угол
наклона к которой хотим определить,
т.е. горизонталь

h₂
║x;

h₂
→ h₁

2 Проводим линию
ската перпендикулярно горизонтали

C₁2₁
┴ h₁

2₁
→ 2₂

3 Определяем
натуральную величину линии ската

2₁2₀
┴ С₁2₁,

2₀2₁
= ∆Z

C₁2₀
– НВ линии ската

4 Определяем искомый
угол

<α
= < (С₁2₁;
С₁2₀)
; <α
– искомый

Аналогичным образом
находятся углы наклона плоскости к
фронтальной и профильной плоскостям
проекций, для чего проводятся фронталь
и профиль соответственно. Алгоритм
решения задачи сохраняется.

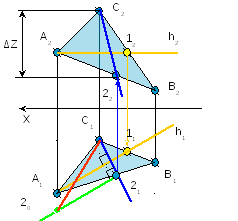
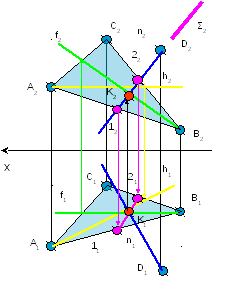
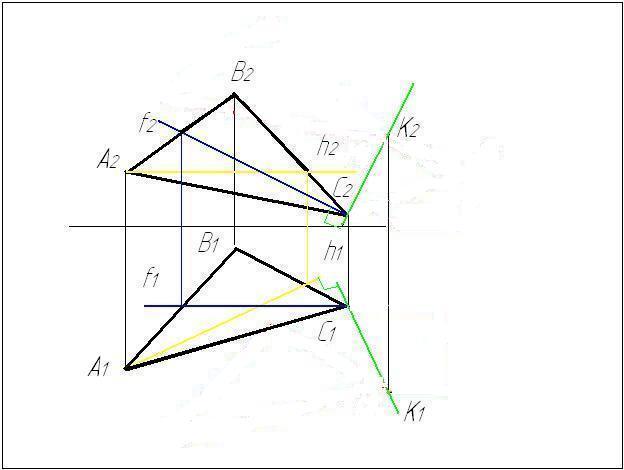
Задача № 2.

Условие задачи:

Найти расстояние
от точки D
до плоскости треугольника АВС.

Исходные данные
к задаче представлены в таблице 1.

Рисунок 2

Решение:

Алгоритм решения
задачи:

1 Через точку
проводим прямую, перпендикулярную
плоскости

n
┴ P(∆ABC)
: n₁┴
h₁;
n₂
┴ f₂;
h₂||х;
f₁||х

2 Определяем
основание перпендикуляра, т.е. точку
пересечения прямой и плоскости

n₂
ЄΣ₂,
Σ┴П₂

12= Σ
∩ Р(АВС);

К₁=1₁2₁
∩ n₁

K₁
→ K₂

(·)K=n
∩ P(ABC)

3 Находим натуральную
величину полученного отрезка

Из ∆К2D₂D₀
:

D₂D₀=
∆Y

K₂D₂
– проекция KD

значит – K₂D₀
– НВ отрезка KD

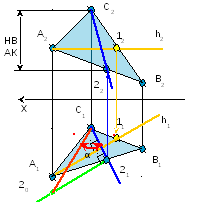
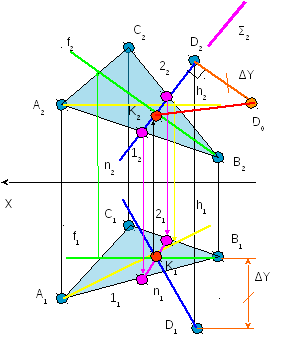
Задача № 3.

Условие задачи:

Определить
линию пересечения плоскостей, заданных
треугольниками ΔАВС и ΔDEF.
Определить видимость.

Исходные данные
к задаче представлены в таблице 1.

Рисунок 3

Решение:

Существует несколько
способов решения данной задачи.
Использовать можно любой из них. Мы
рассмотрим только один.

Для определения
линии пересечения треугольников дважды
решается задача на нахождение точки
пересечения плоскости треугольника с
прямой, принадлежащей другому треугольнику.
Через две найденные точки проводят
линию пересечения треугольников.

Алгоритм решения
задачи следующий:

1 Заключить одну
из сторон треугольника в проецирующую
плоскость. Определить точку пересечения
прямой, принадлежащей плоскости Р с
плоскостью Q.

С₂В₂
ЄΣ₂
; Σ(Σ₂)
┴ П₂

1₂2₂
→ 1₁2₁

N₁=1₁2₁
∩ C₁B₁ N₁
→ N₂

2 То же самое
проделать с другой прямой.

E₁D₁
Є Θ₁
;

Θ(Θ₁)
┴ П₁

3₁4₁
→ 3₂4₂

M₂=3₂4₂
∩E₂D₂

M₂
→ M₁

3 Соединить
полученные точки – это будет NM

N₁M₁,
N₂M₂
– проекции искомой линии пересечения
плоскостей

4 Определить
видимость плоскостей

Видимость на П₁
:

5,3 –конкурирующие
точки. Видимой будет точка, которая
находится дальше от оси Х, т.е. 3₂
дальше, чем 5₂,
следовательно, точка 3₁
принадлежащая отрезку А₁С₁
будет видна.

Видимость на П₂
:

1,6 –конкурирующие
точки. Видимой будет точка, которая
находится дальше от оси Х, т.е. 1₁
дальше, чем 6₁,
следовательно, точка 1₂
принадлежащая отрезку Е₂D₂
будет видна.

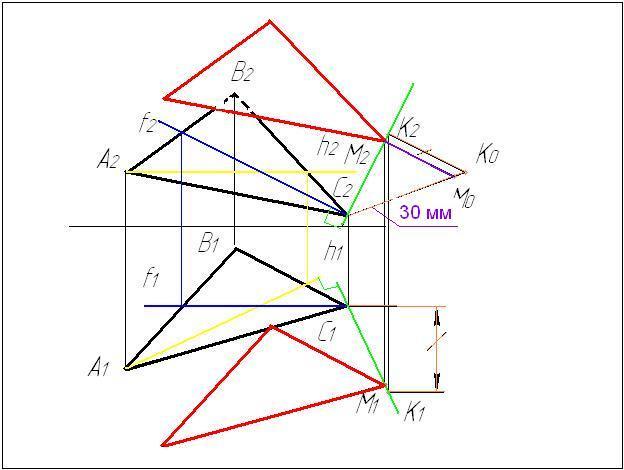
Задача № 4.

Условие задачи:

Построить
плоскость равную и параллельную плоскости
ΔАВС и отстоящую от нее на расстоянии
30 мм. Определить видимость.Исходные
данные к задаче представлены в таблице
1.

Решение:

Алгоритм решения
задачи следующий:

1 Из любой вершины
треугольника проводим прямую,
перпендикулярно плоскости ΔАВС.

n
┴ P(∆ABC)
: n₁┴
h₁;
n₂
┴ f₂;
h₂||х;
f₁||х

2 На прямой выбираем
произвольную точку К (К₁,К₂).

К₁€n₁,
K₂€n₂

3 Находим натуральную
величину отрезка СК

Из ∆К₂С₂К₀
:

К₂К₀=
∆Y

K₂С₂
– проекция KС

значит – С₂К₀
– НВ отрезка KС

4 На натуральной
величине откладываем нужное нам
расстояние 30 мм и находим проекции новой
точки на прямой n.

5 Через найденную
точку проводим прямые, параллельно
сторонам ΔАВС. Необходимо проконтролировать,
чтобы вершины построенного треугольника
находились в проекционной связи.

6 Определяем
видимость треугольников.

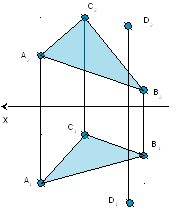
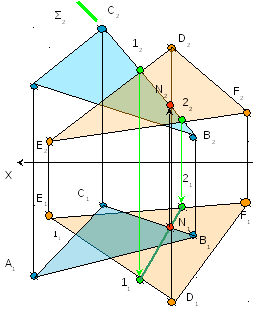
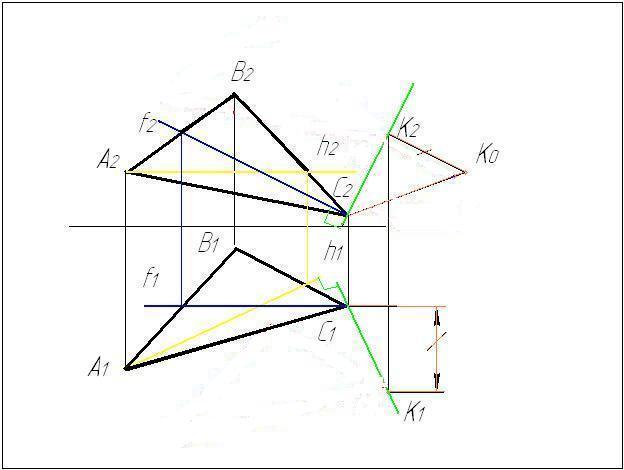
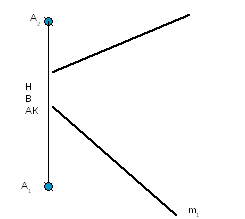
Задача № 5.

Условие задачи:

Найти расстояние
от точки А до прямой m
заданной отрезком ВС. Исходные данные
к задаче представлены в таблице 1.

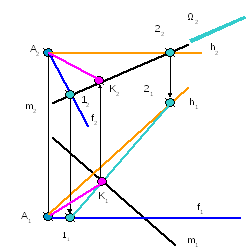
Рисунок 4

Решение:

Алгоритм решения
задачи следующий:

1 Через точку А
проводим плоскость, перпендикулярную
прямой m
(ВС).

Σ(h
∩ f):
f₂
┴m₂,
f₁║x

h₁
┴m₁,
h₂║x

Σ(h
∩ f)
┴ m

2 Находим точку
пересечения прямой m
и плоскости Σ(h
∩ f)

m₂
Є Ω₂,
Ω
┴ П₂

Ω₂
∩ Σ₂
= 1₂2₂,
1₂2₂
→1₁2₁

1₁2₁
∩ m₁
=K₁,
K₁
→K₂

3 Определяем НВ
отрезка АК – расстояние от точки А до
прямой m

Из ∆А₂К₂А₀
:

А₂А₀
= ∆Y
(A₁K₁)

A₂K₂
– проекция АК,

значит – А₀К₂
– НВ АК

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Угловой коэффициент касательной как тангенс угла наклона

(blacktriangleright) Если уравнение прямой задано в виде (>) , то число (k) называется угловым коэффициентом.

(blacktriangleright) Угол (alpha) наклона прямой – это угол между этой прямой и положительным направлением оси (Ox) ( (0leqslant alpha 0) ,

если (alpha>90^circ) , то (k

Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.

Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.

Основные моменты

Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции, она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.

Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.

тангенс угла наклона аппроксимационной прямой

Зависимость max расстояния, на которое может укатиться лыжник от начала горки, от угла наклона горки
Не могу додуматься как забить в Matlab. Если есть хоть какие-то предположения!!Пишите)) Буду очень.

Угол наклона прямой
Здравствуйте! У меня такой вопрос: при построении прямой получается угол наклона b=-1,19 а, по.

Как найти тангенс угла наклона. Электромагнитная индукция
Найти тангенс наклона = дельта l/ дельта v При v=-10 l=-0,3 v=-8 l=-0,24 v=-6 l=-0,18 .

Определение угла наклона прямой
Доброго времени суток. Задача возникла. Для наглядности вывожу на панель линию по двум точкам и.

Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.

Вычисление угла наклона одной прямой относительно другой
Как узнать угол наклона одной прямой относительно другой, если обе прямые заданы координатами двух.

Тангенс угла в прямоугольном треугольнике зная тангенс другого угла
Пускай имеем прямоугольный треугольник. Знаем тангенс одного из не прямых углов. Как найти тангенс.

Изменение координат прямой при изменение угла наклона
Есть прямая координаты точек то есть линия лежит на оси х как изменятся координаты если один конец.

Расчет угла наклона плоскости через углы наклона к осям координат и обратно
Добрый вечер уважаемые математики, возможно вам нетрудно будет подсказать ламеру пару формулок. .

Ввести с клавиатуры радианную меру угла. Определить, что больше: тангенс или котангенс этого угла
Ввести с клавиатуры радианную меру угла. Определить, что больше значение тангенса или котангенса.

Определение угла наклона прямой

Определение угла наклона отрезка
Есть отрезок, который имеет координаты начала (x,y) и конца (x1,y1). Как вычислить угол наклона.

Класс “Прямая”, определить поля с коэффициентом наклона прямой и ее смещением
В классе определить поля с коэффициентом наклона прямой и смещением ее (параметры k и b из.

Определение угла поворота изображения
Всем привет! Столкнулся с следующей проблемой: имеется сканированное изображение (после.

определение азимута и угла места на геостационарный спутник
пищу программу для определение азимута и угла места на геостационарный спутник. есть готовая.

Заказываю контрольные, курсовые, дипломные и любые другие студенческие работы здесь.

тангенс угла наклона аппроксимационной прямой
Добрый вечер. Собственно есть точки по оси абсцисс и ординат. Надо найти тангенс угла наклона.

Вычисление угла наклона одной прямой относительно другой
Как узнать угол наклона одной прямой относительно другой, если обе прямые заданы координатами двух.

Определение угла наклона плоскости по которому скользит тело
По наклонной плоскости скользит тело и в конце третьей секунды достигает скорости 10,9м/с2.

Изменение координат прямой при изменение угла наклона
Есть прямая координаты точек то есть линия лежит на оси х как изменятся координаты если один конец.

Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач

Содержание:

Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.

Угол наклона прямой и угловой коэффициент прямой

Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.

Угол наклона прямой к оси О х , расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.

Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π ) .

Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.

Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.

Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.

Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.

Посчитать угловой коэффициент прямой при угле наклона равном 120 ° .

Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = – 3 .

Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k 0 , тогда угол тупой, что дает право определить его по формуле α = π – a r c t g k .

Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .

Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .

Ответ: α = a r c t g 3 .

Найти угол наклона прямой к оси О х , если угловой коэффициент = – 1 3 .

Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х . Отсюда k = – 1 3 0 , тогда необходимо применить формулу α = π – a r c t g k При подстановке получим выражение:

α = π – a r c t g – 1 3 = π – a r c t g 1 3 = π – π 6 = 5 π 6 .

Ответ: 5 π 6 .

Уравнение с угловым коэффициентом

Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси О у .

Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М , M 1 ( x 1 , y 1 ) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.

Задана прямая с угловым коэффициентом y = 1 3 x – 1 . Вычислить, принадлежат ли точки M 1 ( 3 , 0 ) и M 2 ( 2 , – 2 ) заданной прямой.

Необходимо подставить координаты точки M 1 ( 3 , 0 ) в заданное уравнение, тогда получим 0 = 1 3 · 3 – 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.

Если подставим координаты точки M 2 ( 2 , – 2 ) , тогда получим неверное равенство вида – 2 = 1 3 · 2 – 1 ⇔ – 2 = – 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.

Ответ: М 1 принадлежит прямой, а М 2 нет.

Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 ( 0 , b ) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х , где k = t g α .

Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x – 1 . Получим, что прямая пройдет через точку с координатой 0 , – 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х . Отсюда видно, что коэффициент равен 3 .

Уравнение прямой с угловым коэффициентом, проходящей через заданную точку

Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 ( x 1 , y 1 ) .

Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 ( x 1 , y 1 ) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y – y 1 = k · ( x – x 1 ) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 ( x 1 , y 1 ) .

Составьте уравнение прямой, проходящей через точку М 1 с координатами ( 4 , – 1 ) , с угловым коэффициентом равным – 2 .

Решение

По условию имеем, что x 1 = 4 , y 1 = – 1 , k = – 2 . Отсюда уравнение прямой запишется таким образом y – y 1 = k · ( x – x 1 ) ⇔ y – ( – 1 ) = – 2 · ( x – 4 ) ⇔ y = – 2 x + 7 .

Ответ: y = – 2 x + 7 .

Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами ( 3 , 5 ) , параллельную прямой y = 2 x – 2 .

По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x – 2 , отсюда следует, что k = 2 . Составляем уравнение с угловым коэффициентом и получаем:

y – y 1 = k · ( x – x 1 ) ⇔ y – 5 = 2 · ( x – 3 ) ⇔ y = 2 x – 1

Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно

Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.

Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x – x 1 a x = y – y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y – b = k · x ⇔ k · x k = y – b k ⇔ x 1 = y – b k .

Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.

Привести уравнение прямой с угловым коэффициентом y = – 3 x + 12 к каноническому виду.

Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:

y = – 3 x + 12 ⇔ – 3 x = y – 12 ⇔ – 3 x – 3 = y – 12 – 3 ⇔ x 1 = y – 12 – 3

Ответ: x 1 = y – 12 – 3 .

Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x – y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.

Дано уравнение прямой вида y = 1 7 x – 2 . Выяснить, является ли вектор с координатами a → = ( – 1 , 7 ) нормальным вектором прямой?

Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:

y = 1 7 x – 2 ⇔ 1 7 x – y – 2 = 0

Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , – 1 , отсюда 1 7 x – y – 2 = 0 . Понятно, что вектор a → = ( – 1 , 7 ) коллинеарен вектору n → = 1 7 , – 1 , так как имеем справедливое соотношение a → = – 7 · n → . Отсюда следует, что исходный вектор a → = – 1 , 7 – нормальный вектор прямой 1 7 x – y – 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x – 2 .

Решим задачу обратную данной.

Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ – A B · x – C B .

Результат и является уравннием с угловым коэффициентом, который равняется – A B .

Задано уравнение прямой вида 2 3 x – 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.

Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:

2 3 x – 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .

Ответ: y = 1 6 x + 1 4 .

Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x – x 1 a x = y – y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:

x a + y b = 1 ⇔ y b = 1 – x a ⇔ y = – b a · x + b .

Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:

x – x 1 a x = y – y 1 a y ⇔ a y · ( x – x 1 ) = a x · ( y – y 1 ) ⇔ ⇔ a x · y = a y · x – a y · x 1 + a x · y 1 ⇔ y = a y a x · x – a y a x · x 1 + y 1

Имеется прямая, заданная уравнением x 2 + y – 3 = 1 . Привести к виду уравнения с угловым коэффициентом.

Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на – 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:

y – 3 = 1 – x 2 ⇔ – 3 · y – 3 = – 3 · 1 – x 2 ⇔ y = 3 2 x – 3 .

Ответ: y = 3 2 x – 3 .

Уравнение прямой вида x – 2 2 = y + 1 5 привести к виду с угловым коэффициентом.

Необходимо выражение x – 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · ( x – 2 ) = 2 · ( y + 1 ) . Теперь необходимо полностью его разрешить, для этого:

5 · ( x – 2 ) = 2 · ( y + 1 ) ⇔ 5 x – 10 = 2 y + 2 ⇔ 2 y = 5 x – 12 ⇔ y = 5 2 x

Ответ: y = 5 2 x – 6 .

Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.

Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = – 1 + 2 · λ .

Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:

x = λ y = – 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .

Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:

x 1 = y + 1 2 ⇔ 2 · x = 1 · ( y + 1 ) ⇔ y = 2 x – 1

Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .

Как найти угол наклона головы по отношению к камере?

Я работаю над проектом, который требует, чтобы я нашел угол между телом человека w.r.t. камера. У меня уже есть координаты позы человека, но я не знаю, как найти угол. Как вы думаете, мне нужно использовать некоторые параметры камеры, такие как фокусное расстояние и внутренние параметры камеры? Я был бы признателен за ваши предложения или любые рекомендации. Спасибо.

круг в центре – это голова человека и камера с другой стороны

Если я создаю геометрию только с одной гранью (треугольник), как это: [CoffeeScript синтаксис] geometry = new THREE.Geometry() geometry.vertices.push(new THREE.Vector3(0, 0, 0)) geometry.vertices.push(new THREE.Vector3(0, 10, 0)) geometry.vertices.push(new THREE.Vector3(0, 10, 10)).

Вы можете получить доступ к следующему коду по этой ссылке: jsfiddle.net/2NPxV Мой код css : .custom_content < display: block, width:200px, height: 30px, margin: 5px 0, padding: 0 0, border: 1px solid #000000, >.left-border-red < border-left: 5px solid red, >Мой код html :

Короче говоря, вы должны знать координаты 3D некоторых точек человека и его проекции 2D на плоскости датчика камеры, а затем использовать PnP (Perspective-n-Point) algoritm для оценки положения камеры относительно человека. Лучше знать калибровку камеры, но вы можете использовать DLT (прямое линейное преобразование) algoritm, если у вас нет этих данных.

Теги: #Как найти угол наклона