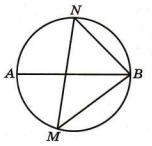
Как найти угол nmb - Исправление недочетов и поиск решений вместе с Examum.ru

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA  =  43°. Найдите угол NMB. Ответ дайте в градусах.

Спрятать решение

Решение.

Угол NBA  — вписанный, поэтому он равен половине дуги, на которую он опирается. Следовательно, дуга AN  =  2∠NBA  =  2 · 43°  =  86°. Диаметр AB делит окружность на две равные части, поэтому величина дуги ANB равна 180°. Откуда дуга NB  =  180° − 86°  =  94°. Угол NMB  — вписанный, поэтому он равен половине дуги, на которую он опирается, то есть равен 94°/2  =  47°.

Ответ: 47.

Источник

Решение:

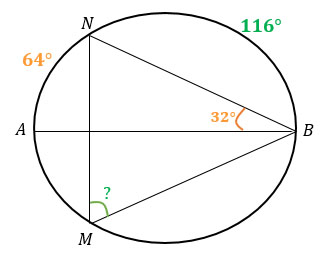
Угол NBA, равный 32°, опирается на дугу AN и является вписанным. Как известно, вписанный угол равен половине дуги, на которую он опирается. Значит, дуга AN в 2 раза больше угла NBA и равна 64°.

Т.к. АВ — диаметр, то он делит окружность на 2 дуги, равные 180° каждая. Найдем дугу NB.

дуга NB = 180° — дуга AN = 180° — 64° = 116°.

Угол NMB опирается на дугу NB и является вписанным, значит он меньше дуги NB в 2 раза и равен 116° : 2 = 58°.

Ответ: 58 (градусы в бланк ответов не пишутся).

Не можешь найти нужную задачу? Предложи свою! Наша группа в VK.

#460

Источник

Размещено 3 года назад по предмету
Математика
от leaderboy98

Ответ на вопрос

Ответ на вопрос дан
таня90

Вписанные углы <NMA=<NBA=43°, т.как опираются на одну дугу АN
<AMB=90°,т.как опирается на диаметр АВ.
Искомый <NMB=<AMB — <NMA=90-43=47°
Ответ на вопрос

Ответ на вопрос дан
katyafink98

Вписанный угол равен половине дуги, на которую он опирается.
дуга NA=43 * 2 = 86⇒дуга NB=180-86=94
Угол NBA = 94/2=47

Информация

Посетители, находящиеся в группе Гости, не могут оставлять комментарии к данной публикации.

Источник

Способ №1
Решение:

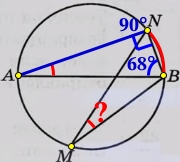
Достроим ΔANB он прямоугольный (вписан в окружность, АВ – гипотенуза и диаметр окружности).
В нём ∠ANB прямой равен 90°. Сумма углов любого треугольника равна 180°. Найдём ∠NAB:

∠NAB = 180° – ∠ANB – ∠NBA = 180° – 90° – 68° = 22°

∠NAB = ∠NMB = 22° как вписанные опирающиеся на одну и туже дугу ‿NB.

Ответ: 22.

Способ №2
Решение:

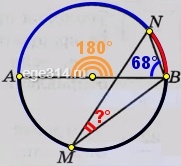
AB – диаметр, делит окружность на две равные части по:

360°/2 = 180°

Заметим, что дуги на которые опираются ∠NBA и ∠NMB в сумме дают 180°:

‿AN + ‿NB = 180°

Дуга ‿AN в два раза больше угла который на неё опирается:

‿AN = 2·∠NBA = 2·68º = 136°

Тогда:

136° + ‿NB = 180°
‿NB = 180° – 136° = 44°

∠NMB равен половине дуги ‿NB на которую опирается:

∠NMB = ‿NB/2 = 44°/2 = 22°

Ответ: 22.

Источник

Задание:

На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол NBA = 41º. Найдите угол NMB. Ответ дайте в градусах.

Решение:

Дуга AN = 41º * 2 = 82º.
Дуга ANB = 180º, так как лежит на развернутом угле.
Тогда дуга NB = дуга ANB — дуга AN = 180º — 82º = 98º.
Тогда угол NMB = 98º / 2 = 49º.

Ответ: 49.

Оценка: 2.7 из 7

Комментарии

Всего комментариев: 0

Источник