Как найти угол образованный двумя высотами

Как найти угол между высотами треугольника? Зависит ли величина угла от вида треугольника?

Утверждение.

Один из углов, образованный высотами треугольника, проведёнными из двух его вершин, равен углу при третьей вершине.

Другой угол равен сумме углов треугольника, из вершин которых проведены высоты.

Доказательство:

1 способ

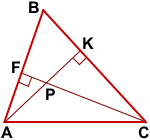
Рассмотрим остроугольный треугольник ABC.

Пусть AK и CF — его высоты.

Тогда ∠BFC=∠BKA=90°.

Так как сумма углов четырёхугольника равна 360°, то в 4-угольнике BKPF

∠BFP+∠FPK+∠BKP+∠FBK=360°,

откуда ∠FPK+∠FBK=180° и ∠FPK=180°-∠FBK.

∠FPK+∠KPC=180° (как смежные).

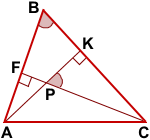
∠KPC=180°-∠FPK=180°-(180° -∠FBK)=∠FBK.

Так как сумма углов треугольника равна 180°,

∠BAC+∠FBK+∠ACB=180°,

∠FBK=180°-(∠BAC+∠ACB),

∠FPK=180°-∠FBK=180° -(180° -(∠BAC+∠ACB))=∠BAC+∠ACB.

2 способ

Прямоугольные треугольники BCF и PKC подобны по общему острому углу C. Следовательно, ∠KPC=∠FBC.

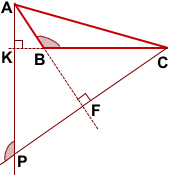
Если треугольник ABC — тупоугольный, рассуждения и вывод аналогичны.

Утверждение верно и для прямоугольного треугольника.

То есть для любого треугольника ABC один из углов между высотами, проведёнными из вершин A и C, равен углу B, другой — сумме углов A и C.

В частности, один угол между высотами равностороннего треугольника равен 60°, другой — 120°:

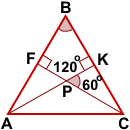
∠KPC=60°,

∠FPK=120°.

Высота треугольника — подробнее

Высота – линия, проведённая из вершины треугольника перпендикулярно противоположной стороне (прямой, которая эту сторону содержит).

На этом рисунке ( displaystyle BH) – высота.

Но иногда высота (в отличие от биссектрисы и медианы) ведёт себя, как непослушный ребенок – «выбегает» из треугольника. Это бывает в тупоугольном треугольнике.

И тогда получается так:

В общем, не нужно пугаться, если основание высоты оказалось не на стороне треугольника, а «за» треугольником, на продолжении стороны.

Как же решать задачи, в которых участвует высота?

Нужно стремиться применить какие-нибудь знания о прямоугольном треугольнике – ведь где высота – там и прямой угол.

Но попадаются задачи и похитрее, при решении которых лучше обладать дополнительными знаниями заранее, а не выводить их «с нуля». Сейчас мы обсудим некоторые из них.

Но для начала решим простенькую задачку на высоту в тупоугольном треугольнике:

В треугольнике ( displaystyle ABC) с тупым углом ( displaystyle C) проведена высота ( displaystyle BH). Найти ( displaystyle AC), если ( AB=2sqrt{10}), ( BC=sqrt{13}), ( BH=2).

Смотри: из-за того, что угол ( C) – тупой, высота ( BH) опустилась на продолжение стороны ( AC), а не на саму сторону.

Теперь давай увидим во всём этом два прямоугольных треугольника.

Смотри их целых два:

Применяем теорему Пифагора к треугольнику ( BCH):

( B{{C}^{2}}=B{{H}^{2}}+C{{H}^{2}}), то есть ( 13=4+C{{H}^{2}}); ( CH=3).

А теперь теорема Пифагора для ( Delta ABH):

( A{{B}^{2}}=A{{H}^{2}}+B{{H}^{2}}); то есть ( 40=A{{H}^{2}}+4); ( AH=6).

Теперь осталось только заметить, что ( AC=AH-CH=6-3=3).

Нашли!

А теперь давай вернемся к нашим высотам!

Остроугольный треугольник и высота

Вернёмся–ка к остроугольному треугольнику. Отметим на рисунке равные углы:

Что видим теперь? Ещё подобные треугольники!

Как от двух линий вообще могут получиться столько подобных треугольников?!

Но тем не менее…

( Delta C{{H}_{C}}Bsim Delta C{{H}_{A}}Hsim Delta A{{H}_{A}}Bsim Delta A{{H}_{C}}H)

Видишь, какое богатство? И всё это может быть использовано в задачах!

Ну вот, теперь ты узнал что-то новенькое про высоты треугольника.

Теперь пробуй применять в задачах всё это – и соображение о том, что высота образует прямоугольный треугольник, и простые подобия прямоугольных треугольников, получающихся при пересечении двух высот, и подобие похитрее — которое с косинусом, и то, что угол между высотами равен углу между сторонами…

Главное, ты не старался просто запоминать все эти факты, а осознай, что их можно очень просто вывести.

И тогда, если ты будешь точно знать, например, что две проведённые высоты приносят кучу бонусов в виде всяких подобий, то ты непременно и сам получишь все эти бонусы, а заодно – решение своей задачи!

Спрятать решение

Что такое двугранный угол

Двугранным углом называют геометрическую фигуру, которая сформирована парой полуплоскостей, выходящие из общей прямой.

Заметим, что угол, измеряемый в градусах, разделяющий пару плоскостей, является минимальным из количества двугранных углов, которые сформированы в результате пересечения плоскостей.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Источник: ru.wikipedia.org

Как найти

В поиске ответов на различные примеры из геометрии следует руководствоваться основными понятиями. Введем несколько обозначений для элементов двугранного угла.

Грани двугранного угла представляют собой полуплоскости, которые образовали данный угол.

Ребро двугранного угла является единой прямой для рассматриваемых полуплоскостей.

В процессе измерения двугранных углов используют величины линейных углов, то есть тех, что образованы при пересечении двугранного угла и плоскости, расположенной под прямым углом к ребру рассматриваемого угла. В результате для поиска величины двугранного угла рекомендуется следовать следующему алгоритму действий:

• следует определить какую-либо точку на его ребре;
• далее под прямым углом к ребру нужно опустить из определенной ранее точки лучи ко всем граням;
• угол, который разделяет изображенные лучи, соответствует величине искомого двугранного угла.

Запишем в табличной форме значения двугранных углов, характерные для правильных многогранников:

В данном случае следует считать (phi) равным (frac{1+sqrt{5}}{2}), то есть золотым сечением.

Виды двугранных углов

Тупой двугранный угол представляет собой такой угол, градусная величина которого превышает значение в 90°.

Тупой двугранный угол:

Источник: rusinfo.info

Прямой двугранный угол является таким двугранным углом, градусная мера которого соответствует 90°.

Прямой двугранный угол:

Источник: rusinfo.info

Острым двугранным углом называют двугранный угол с градусной мерой, равной 90°.

Острый двугранный угол:

Источник: rusinfo.info

Задачи

Решение

Предположим, что искомая пирамида имеет следующее название SABCD. Пусть S играет роль вершины геометрической фигуры, а ее ребра соответствуют а. Тогда, согласно условию задания, требуется найти угол, разделяющий грани SAD и SCD.

Источник: shkolkovo.net

Построим (CHperp SD). Заметим, что:

(triangle SAD=triangle SCD)

В этом случае AH также играет роль высоты в (triangle SAD). Таким образом, исходя из определения:

(angle AHC=alpha)

Заметим, что (alpha) является линейным углом, разделяющим грани SAD и SCD. При условии квадратного основания в пирамиде запишем следующее:

(AC=asqrt2)

Кроме того, имеет место такое равенство:

CH=AH

Высота AH находится в треугольнике с одинаковыми сторонами, равными а. Таким образом:

(CH=AH=frac{sqrt3}2a)

Воспользуемся теоремой косинусов применительно к (triangle AHC):

(cos alpha=dfrac{CH^2+AH^2-AC^2}{2CHcdot AH} =-dfrac13 quadRightarrowquad 6cosalpha=-2.)

Ответ: -2.

Решение

Источник: shkolkovo.net

Заметим, что треугольник AMN обладает прямым углом, тогда:

(AN^2 = AM^2 + MN^2)

В результате:

(AM^2 = 39^2 — 15^2 = 36^2)

Прямоугольным также является треугольник BMN. В таком случае:

(BN^2 = BM^2 + MN^2)

Исходя из этого, получим:

(BM^2 = 17^2 — 15^2 = 8^2)

Воспользуемся теоремой косинусов применительно к треугольнику AMB:

(AB^2 = AM^2 + MB^2 — 2cdot AMcdot MBcdotcosangle AMB)

Таким образом:

(40^2 = 36^2 + 8^2 — 2cdot 36cdot 8cdotcosangle AMBqquadLeftrightarrowqquad cosangle AMB = -dfrac{5}{12})

Исходя из того, что угол (alpha), разделяющий плоскости, является острым, а угол (angle AMB) определяется как тупой, получим следующее равенство:

(cosalpha=dfrac5{12})

(3cosalpha = dfrac54=1,25)

Ответ: 1,25.

Решение

Источник: shkolkovo.net

Геометрические фигуры в виде треугольников с прямыми углами (triangle SAO) и (triangle SDO) являются идентичными, согласно паре сторон и углу, который их разделяет:

(SO perp ABC Rightarrow angle SOA = angle SOD = 90^circ)

AO = DO

Записанные выше равенства являются справедливыми, так как в точке O пересекаются диагонали квадрата, а SO служит общей стороной.

(Rightarrow AS = SD Rightarrow triangle ASD)

(triangle ASD) является равнобедренным. Точка K делит пополам AD. В таком случае SK представляет собой высоту в треугольнике (triangle ASD), а OK обозначает высоту в треугольнике AOD. Таким образом, плоскость SOK расположена под прямым углом к плоскостям ASD и ABC. Можно сделать вывод о том, что (angle SKO)  является линейным углом, который соответствует искомому двугранному углу.

Источник: shkolkovo.net

Рассмотрим треугольник (triangle SKO):

(OK = frac{1}{2}cdot AB = frac{1}{2}cdot 10 = 5 = SO)

Таким образом, (triangle SOK) является равнобедренным прямоугольным треугольником. Тогда:

(angle SKO = 45^circ.)

Ответ: (45^circ.)

Как найти угол между высотами треугольника? Зависит ли величина угла от вида треугольника?

Утверждение.

Один из углов, образованный высотами треугольника, проведёнными из двух его вершин, равен углу при третьей вершине.

Другой угол равен сумме углов треугольника, из вершин которых проведены высоты.

Доказательство:

1 способ

Рассмотрим остроугольный треугольник ABC.

Пусть AK и CF — его высоты.

Тогда ∠BFC=∠BKA=90°.

Так как сумма углов четырёхугольника равна 360°, то в 4-угольнике BKPF

∠BFP+∠FPK+∠BKP+∠FBK=360°,

откуда ∠FPK+∠FBK=180° и ∠FPK=180°-∠FBK.

∠FPK+∠KPC=180° (как смежные).

∠KPC=180°-∠FPK=180°-(180° -∠FBK)=∠FBK.

Так как сумма углов треугольника равна 180°,

∠BAC+∠FBK+∠ACB=180°,

∠FBK=180°-(∠BAC+∠ACB),

∠FPK=180°-∠FBK=180° -(180° -(∠BAC+∠ACB))=∠BAC+∠ACB.

2 способ

Прямоугольные треугольники BCF и PKC подобны по общему острому углу C. Следовательно, ∠KPC=∠FBC.

Если треугольник ABC — тупоугольный, рассуждения и вывод аналогичны.

Утверждение верно и для прямоугольного треугольника.

То есть для любого треугольника ABC один из углов между высотами, проведёнными из вершин A и C, равен углу B, другой — сумме углов A и C.

В частности, один угол между высотами равностороннего треугольника равен 60°, другой — 120°:

∠KPC=60°,

∠FPK=120°.

Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.

Угол треугольника через три стороны

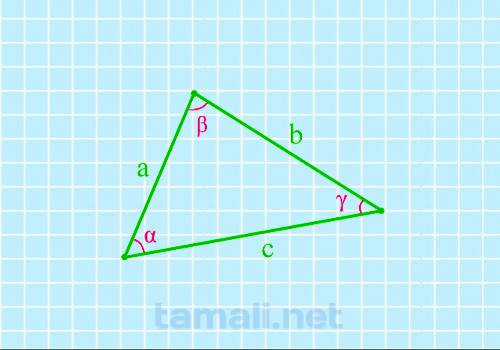
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить

cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb

где a, b, c — стороны треугольника.

Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.

Угол прямоугольного треугольника через две стороны

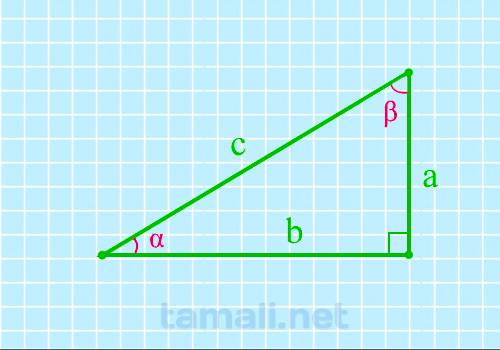
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.

sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a

где a, b — катеты, c — гипотенуза.

Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.

Острый угол прямоугольного треугольника через катет и площадь

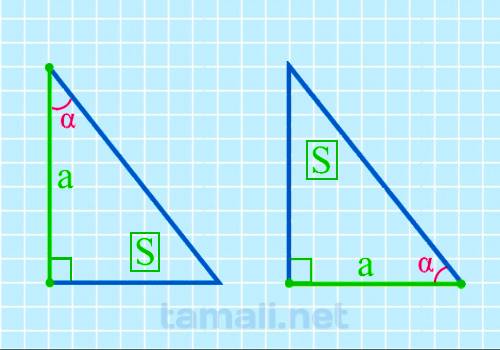
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:

tg(α) = a² / 2S

где a — катет, S — площадь прямоугольного треугольника.

Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.

Угол треугольника через высоту и катет

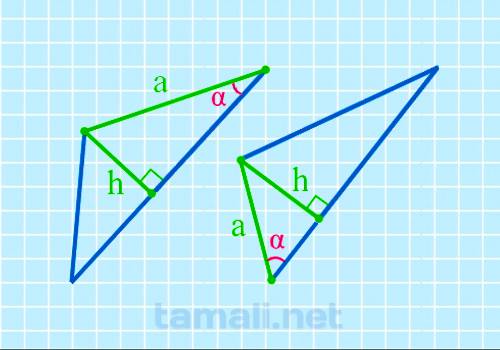
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.

sin α = h / a

где h — высота, a — катет.

Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°

Угол при основании равнобедренного треугольника через биссектрису и основание

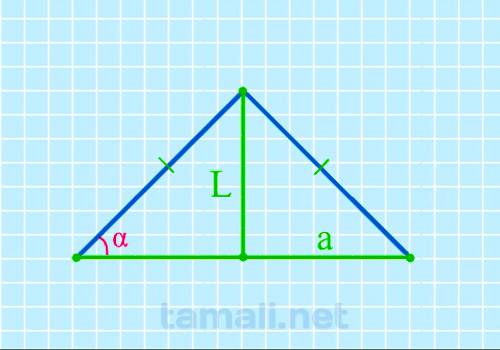
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:

tg α = L / (a/2)

где L — биссектриса, a — основание.

Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º

Угол при основании равнобедренного треугольника через биссектрису и боковую сторону

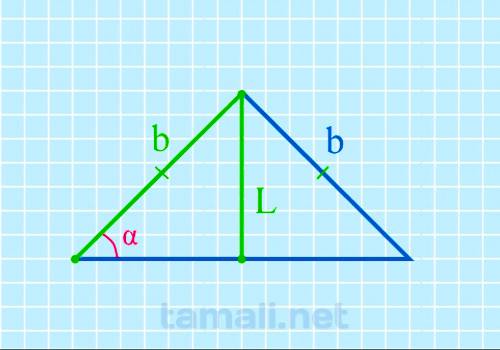
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:

sin α = L / b

где L — биссектриса, b — боковая сторона.

Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.

Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону

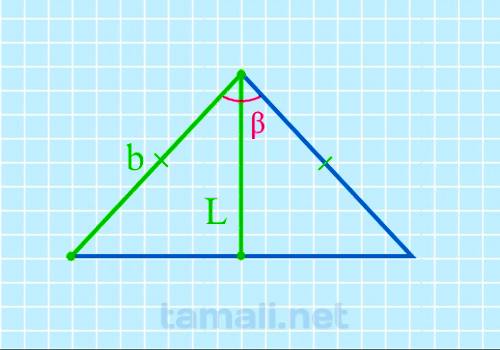
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).

2cos(β) = L / b

где L — биссектриса, b — боковая сторона.

Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º

Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону

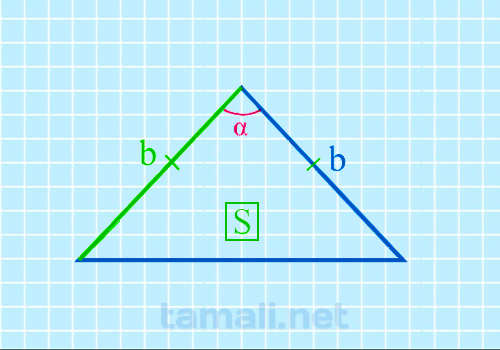
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:

sin(α) = 2S / b²

где b — боковая сторона равнобедренного треугольника, S — площадь.

Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º

Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.

Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.