Как найти угол осколка

2016-09-17   

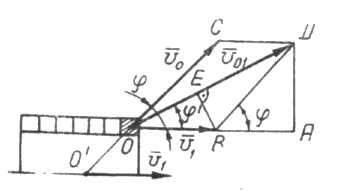
В результате взрыва снаряда массой $m$, летевшего со скоростью $v$, образовались два одинаковых осколка. Пренебрегая массой взрывчатого вещества, найдите максимальный угол разлёта осколков, если сразу после взрыва их общая кинетическая энергия увеличилась на величину $Delta W$.

Решение:

В системе отсчёта, движущейся вместе со снарядом, в соответствии с законом сохранения импульса скорости осколков сразу после взрыва одинаковы: $vec{v}_{1c} = — vec{v}_{2c}$. В неподвижной системе отсчёта скорости первого и второго осколков равны $vec{v}_{1} = vec{v} + vec{v}_{1c}$ и $vec{v}_{2} = vec{v} + vec{v}_{2c}$ соответственно (см. рис.). Согласно условию задачи,

$Delta W = frac{mv_{1}^{2}}{4} + frac{mv_{2}^{2}}{4} — frac{mv^{2}}{2}$.

Из записанных соотношений получаем: $v_{1c}^{2} = 2 Delta W /m$.

Обозначим через $alpha$ угол разлёта осколков, а через $beta$ между векторами $vec{v}$ и $vec{v}_{1c}$. Тогда по теореме косинусов рис.)

$v_{1}^{2} = v^{2} + v_{1c}^{2} + 2vv_{1c} cos beta$,

$v_{2}^{2} = v^{2} + v_{1c}^{2} — 2vv_{1c} cos beta$,

$(2v_{1c})^{2} = v_{1}^{2} + v_{2}^{2} — 2v_{1}v_{2} cos alpha$,

откуда получаем:

$cos alpha = frac{v^{2} — v_{1c}^{2}}{ sqrt{(v^{2} + v_{1c}^{2})^{2} — 4v^{2}v_{1c}^{2} cos^{2} beta}}$.

Максимальный угол разлёта осколков $alpha_{max}$ лежит в пределах от $0$ до $pi$, a $cos alpha_{max}$ — в пределах от 1 до —1. Если $v < v_{1c} = sqrt{2 Delta W/m}$, то из полученной формулы следует, что $cos alpha < 0$, и $alpha_{max} = pi$ достигается при $beta = 0$, то есть осколки летят в разные стороны вдоль первоначального направления полёта снаряда. Если $v = v_{1c}$, то $alpha = pi/2$ при всех $beta$, кроме $beta = 0$, когда один из осколков останавливается $(v_{2} = 0)$, и угол разлёта не определён. Если же $v > v_{1c} = sqrt{2 Delta W /m}$, то $cos alpha > 0$, и $alpha_{max}$ достигается при минимальном значении $cos alpha$, то есть при $beta = pi/2$. При этом

$cos alpha_{max} = frac{v^{2} — v_{1c}^{2}}{v^{2} + v_{1c}^{2}} = frac{mv^{2} — 2 Delta W}{mv^{2} + 2 Delta W}$.

Снаряд, летевший в
горизонтальном направлении со скоростью 20 м/с , разорвался на два осколка
массами 10 кг и 5 кг. Скорость меньшего осколка равна 20 м/с и направлена
вертикально вверх. Определите модуль и направление скорость движения большего
осколка.

Решение.

Материальными объектами
задачи являются: снаряд, два осколка, поверхность Земли, гравитационное поле
Земли и воздух. Снаряд и осколки примем за материальные точки.

Систему отсчета свяжем
с поверхностью Земли и будем считать ее инерциальной. Начало координат выберем
на поверхности Земли. Ось OX
направим горизонтально в направлении движения снаряда, ось OY – вертикально вверх.

В физическую систему
включим

снаряд и осколки. Земля и воздух по отношению к выделенной физической
системе являются внешними телами. Даже если не учитывать взаимодействие
физической системы с воздухом, она будет незамкнутой. Это обусловлено действием
на тела системы ничем не скомпенсированной силы тяжести.

Можно выделить два
состояния системы: начало взрыва и конец взрыва. Если учесть, что промежуток
времени между началом и концом взрыва небольшой, а внутренние силы, возникающие
при этом, велики по сравнению с силой тяжести, то выделенную физическую систему
можно считать практически замкнутой и описать законом сохранения импульса.

Начальный импульс
физической системы равен p₁ = (m₁ + m₂)v , а ее конченый импульс – p₂ = m₁v₁ + m₂v₂ .

Согласно закону сохранения
импульса: p
= p₂ или

.

Если спроецировать
векторные величины на оси координат, получим

.

Откуда

.

Расчеты дают: v₁ = 32 м/с, α = 19° . Таким образом, скорость большого осколка
равна 32 м/с и направлена вниз под углом α = 19° к горизонту.

Ответ: v₁ = 32 м/с, α = 19° .

Источник: Физика. Полный курс подготовки к ЦТ.  Под общей редакцией проф. В.А. Яковенко.

При
взрыве ЬЧ образуется осколочное поле
— поток оскол­ков, характеризующихся
направлением и скоростью движения, а
также плотностью, т. е. количеством
осколков, приходящихся единицу той
площади, которую они пересекают. Плотность
потока осколков является одной из
важнейших характеристик, определяющих
возможность попадания осколков в цель.
Так как сама цель в общем случае может
находиться под совер­шенно произвольным
направлением по отношению к оси БЧ, то
при решении задачи по определению
вероятности попадания ос­колков в
цель необходимо прежде всего знать,
сколько вообще осколков летит в данном
направлении. Ответ на данный вопрос
дает так называемый закон разлета
осколков. Он представля­ет собой
зависимость относительного числа
осколков, летящих в заданном направлении
относительно оси БЧ. Обычно это
на­правление задается в сферичес­кой
системе координат двумя уг­лами —
углом

в экваториаль­ной и углом

в меридианной плоскостях (рисунок
9.10).

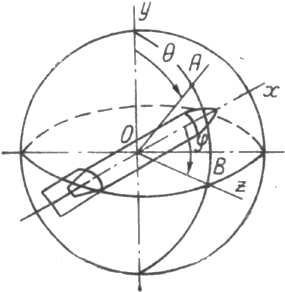
Рисунок.
9.10. Углы

и

,
определя­ющие закон

разлета
осколков

Угол

отсчитывается от оси БЧ и мо­жет
изменяться от 0 до

..
Угол

изменяется от 0 до 2
,
а на­чало его отсчета выбирается
про­извольно ввиду симметрии БЧ и,
следовательно, постоянной плотности
потока осколков для всех направлений,
определяемых этим углом. Таким образом,
за­дача нахождения закона разлета
сводится к определению относи­тельного
количества осколков, летящих в
направлениях, определяемых углом

в меридиан­ной плоскости. Решение
этой задачи может быть получено как
теоретически, так и опытным путем.
Теоретический способ определения закона
разлета основан на некоторых исходных
предпосылках. Например, из чисто
фи­зических представлений ясно, что
сферическая боевая часть при инициировании
заряда из центра образует осколочное
поле, имеющее по крайней мере в начальный
момент разлета вид сферической поверхности
с постоянной плотностью потока ос­колков.
В этом случае зависимость

характеризует распре­деление
относительного количества осколков,
летящих в нап­равлениях, определяемых
углом

(рисунок 9.11) и приходящих­ся на единичный
угол. В самом деле, если общее количество
осколков равно

,
то на сфере радиуса

создается плотность потока осколков,
равная

.
Размер площадки, опре­деляемой углами

и

,
в этом случае будет равен

.

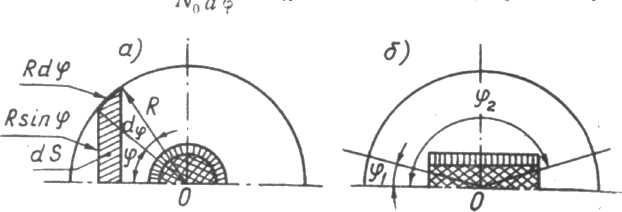
Рисунок
9.11. Определение законов разлета:

а
— сферической и б — цилиндрической БЧ

Тогда
относительное число осколков
приходящихся на площадку

,
будет равно

,
что дает

при

(9.14)

Точно
так же можно поступить и при рассмотрении
цилин­дрической БЧ. Можно предположить,
что к моменту взрыва цилиндрическая
оболочка приобретает бочкообразную
форму, поверхность которой близка к
сферической. Можно также счи­тать,
что плотность потока осколков является
постоянной. Тогда, находя углы

и

,
определяющие относительно оси БЧ, так
называемые «мертвые зоны», в соответствии
с (5.14) можно получить

0
при

при

(9.15)

0
при

В
выражении (9.15) нормирующий множитель
находится из условия

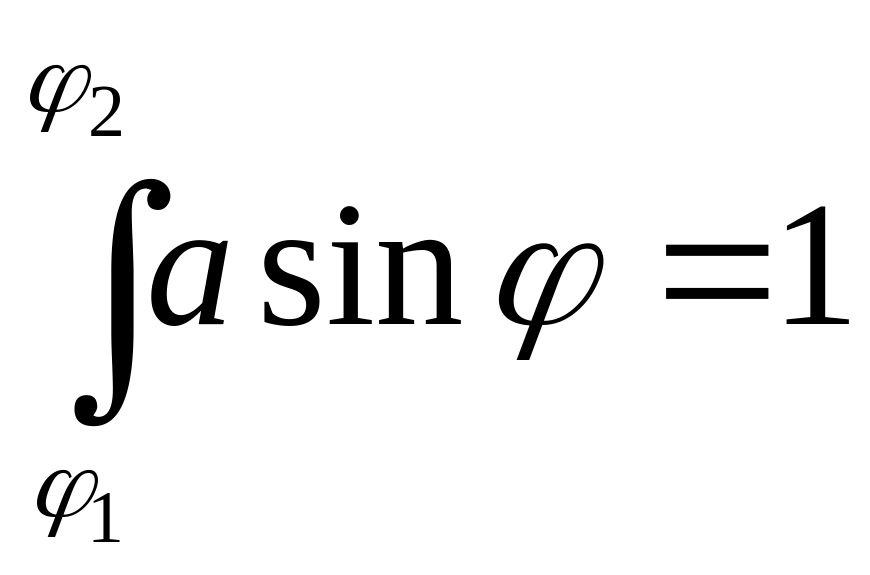
что
дает

Экспериментальный
способ определения законов разлета
осколков предполагает подрыв БЧ в
специальной мишенной обстановке,
представляющей собой полуцилиндр,
улавливаю­щий часть осколков, летящих
в направлении, определяемом двугранным
углом

(рисунок 9.12).

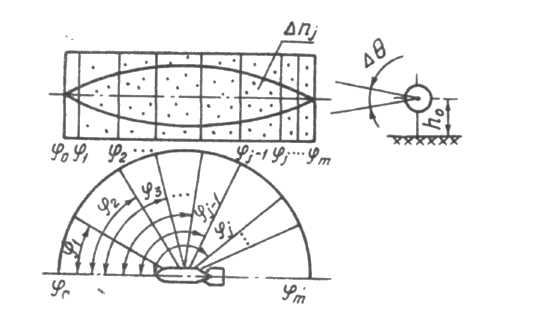
Рисунок
9.12. Мишенная обстановка для определения
закона

разлета осколков

Щиты
полуцилиндра уста­навливаются на
одинаковом расстоянии R
от центра БЧ. Угол

разбивается на угловые секторы шириной

,
границы которых на щитах обозначены
верти­кальными линиями. Линии
пересечения полуцилиндра плоскостя­ми
двугранного угла вместе с вертикальными
линиями образу­ют площадки, улавливающие
осколки, летящие в направлениях,
ограниченных углами

и

.
При взрыве БЧ в щитах обра­зуются
пробоины, число

,
которых подсчитывается в каждой площадке.
Число

.
увеличивается в

раз и тем са­мым определяется количество
осколков

,
летящих в угло­вом секторе шириной

,
примыкающем к углу

,.
Далее находится относительное число
осколков

и рассчиты­вается соответствующая
высота столбца гистограммы

(9.16)

Примерный
вид гистограммы (5.16), а также сглаживаю­щая
кривая

приведены на рисунке. 9.13, а.

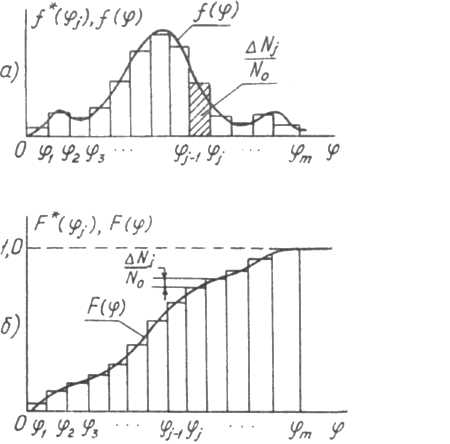
Рисунок
9.13. Гистограммы

и выравнивающие кривые

диффе­ренциального
а) и интегрального б) за­конов
распределения осколков по напра­влениям
разлета

Аналогичным
образом можно построить статистическую
за­висимость

(5.17)

в
которой

количество осколков, летящих в конусе,
определяемом углом

,
относительно оси БЧ.

На
рис 9.13, б приведены примерный вид
гистограммы (9.17), а также сглаживающая
кривая

.
Функции

и

принято называть соответственно
дифференциальным и интегральным законами
распределения осколков по направлениям
разлета. Между собой они связаны
соотношениями

,

(5.18)

Наличие
гистограмм и соответствующих
сглаживающих кривых позволяет решать
следующие задачи:

—
находить количество осколков

,
летящих между коническими поверхностями,
определяемыми углами

и

;

—
определять среднее направление разлета
осколков

;

—
рассчитывать плотность потока осколков
в заданной точ­ке осколочного поля.

При
наличии законов распределения

и

величи­ны

и

определяются следующими зависимостями:

(5.19)

(5.20)

При

зависимость (5.19) определяет количество
ос­колков, летящих в конусе, определяемом
углом

.

Важным
вопросом, с которым приходится сталкиваться
при проектировании осколочных БЧ,
является изыскание способов уп­равления
законами разлета ос­колков. На рисунке
9.14 показаны зависимости, характеризующие
изменение характера функций J{f)
при изменении положения точки инициирования
цилиндри­ческой БЧ и изменении формы
самой БЧ.

Следует
подчеркнуть, что наличие аналитических
выражений для законов разлета осколков
дает возможность решать целый ряд
обратных задач. Например, может оказаться
необ­ходимым определить такую форму
БЧ, при которой в данном направлении
обеспечивается требуемая плотность
потока ос­колков.

Рассмотренные
законы распределения характеризуют
отно­сительное количество осколков,
летящих в указанных направ­лениях,
относятся к случаю взрыва неподвижных
БЧ. Поэтому их принято называть законами
разлета осколков в статике. В реальных
условиях взрыва БЧ может иметь скорость
движе­ния

,
поэтому общая абсолютная скорость

каждого ос­колка, а следовательно, и
его направление

,
будут отличаться от тех значений

и

,
которые он имел бы при подрыве не­подвижной
БЧ (рисунок 9.15).

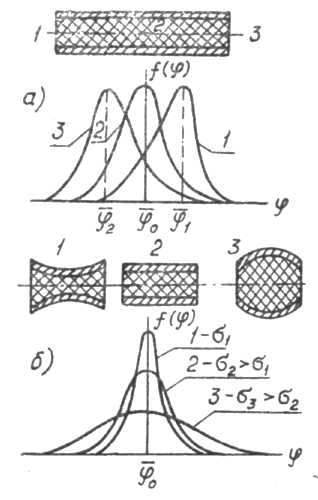
Рисунок
9.14. Управление законом разлета осколков
путем изменения:

а-
точки инициирования 1, 2, 3 и 6 — формы БЧ

Рисунок
9.15. Учет скорости БЧ при оп­ределении
направления и скорости разлета
осколков

В
таком случае необходимо не только
определять начальную скорость движения
осколков

|,
но и перестраивать законы разлета

и

в

и

.
Наиболее просто эта задача решается
применительно к закону

,
так как каждому углу

можно поставить в соответствие угол

у’,
имея в виду, что количество осколков,
летящих в конусах, ограниченных этими
углами, одинаково и, следовательно,
имеет место равенство

.
Из

ОАД рисунка 9.15 находим

(9.21)

Задавшись
несколькими значениями угла

и определив соответствующие значения
угла

,
легко перестроить кривую

в кривую

,
имея в виду равенство значений
интег­рального закона распределения

.

На
рисунке 9.16 показан стрелками порядок
перестроения зави­симости

в

.
Зная зависимость

,
дифференциальный закон распределения
осколков по направлениям разле­та
можно определить, используя соотношения
(5.18).

Рисунок
9.16 Перестроение закона разлета

в

Абсолютная
скорость разлета осколков

при известных скоростях БЧ

и начальной скорости осколков в статике

может быть определена, если известны
значения углов

и

.
Так из

OBD
(рисунок 5.15) по теореме косинусов находим

. (9.22)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Закон сохранения импульса на плоскости

Из кодификатора по физике, 2020.
«1.4.3. Закон сохранения импульса: в ИСО

Теория

Импульс тела — векторная физическая величина, равная произведению массы тела m на его скорость :

— Обозначается буквой , измеряется в килограмм-метр в секунду (кг∙м/с).
— Импульс тела направлен в ту же сторону, что и скорость тела, и наоборот.

Изменение импульса тела

где и — конечный и начальный импульсы тела, и — конечная и начальная скорости тела, m — масса тела.

Импульс системы тел равен векторной сумме импульсов тел входящих в эту систему

где m1, m2, … — массы тел системы, — скорости тел системы.

Изменение импульса системы тел

где — конечный импульс системы тел, — начальный импульс системы тел, m1, m2, … — массы тел системы, — конечные скорости тел системы, — начальные скорости тел системы.

Импульс силы — векторная физическая величина, равная произведению силы на время t ее действия:

— Обозначается буквой , измеряется в Ньютон на секунду (Н∙с).
— Импульс силы направлен в ту же сторону, что и сила, и наоборот.

Закон сохранения импульса:

в инерциальной системе отсчета (ИСО) векторная сумма импульсов всех тел системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему тел, равна нулю.

Задачи на применение закона сохранения импульса тел (системы тел) решайте, придерживаясь следующего плана:

1. Сделайте схематический чертеж. Укажите направления осей координат ОX и ОY.

— Материальную точку изобразите в виде двух прямоугольников (или окружностей) и укажите над ними (если это известно) направления скорости или импульса до и после взаимодействия.
— Индексы скоростей, импульсов на рисунке должны соответствовать индексам скоростей, импульсов в условии.

2. Определите, векторная сумма внешних сил, действующих на систему тел, равна нулю или нет. Если равна нулю, то запишите закон сохранения импульса тел в векторном виде и в проекциях.

Определите значения проекций всех величин.

3. Решите полученные уравнения.
 

к оглавлению ▴

Задачи

Задача 1

Два тела движутся по взаимно перпендикулярным пересекающимся прямым, как показано на рисунке. Модуль импульса первого тела p₁ = 4 кг⋅м/с, а второго тела p₂ = 3 кг⋅м/с . Чему равен модуль импульса системы этих тел после их абсолютно неупругого удара?

Решение. Импульс тел изменяет их столкновение. До удара двигались тела отдельно друг от друга. После неупругого удара тела двигались вместе.

Внешних сил нет, поэтому запишем закон сохранения импульса

1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда импульс тел (направление которого неизвестно) будет равен (рис. 2, а)

Направление осей OХ и OY показаны на рисунке условия. Запишем уравнение (1) в проекциях на оси:

После подстановки уравнений (3) и (4) в (2) получаем:

2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 2, б). Модуль импульса p после удара найдем по теореме Пифагора

 

к оглавлению ▴

Задача 2.

По гладкой горизонтальной плоскости движутся вдоль осей X и Y две шайбы с импульсами, равными по модулю p10 = 5 кг·м/с и p20 = 3 кг·м/с (рис. 3). После их соударения первая шайба продолжает двигаться по оси Y в прежнем направлении. Модуль импульса первой шайбы после удара равен p1 = 2 кг·м/с. Найдите модуль импульса второй шайбы после удара. Ответ округлите до десятых.

Решение. Импульс шайб изменяет их столкновение. До удара шайбы двигались отдельно друг от друга. После удара шайбы так же двигались отдельно.

Внешних сил нет, поэтому запишем закон сохранения импульса

1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда импульс вто-рой шайбы (направление которого неизвестно) будет равен

Направление осей OХ и OY показаны на рисунке 4. Запишем уравнение (1) в проекциях на оси:

После подстановки уравнений (3) и (4) в (2) получаем:

 

к оглавлению ▴

Задача 3.

Лодка массой 100 кг плывет без гребца вдоль пологого берега со скоростью 1 м/с. Мальчик массой 50 кг прыгает с берега в лодку со скоростью 2 м/с так, что векторы скорости лодки и мальчика составляют прямой угол. Определите значение и направление скорости лодки (в см/с) с мальчиком. Ответ округлите до целых.

Решение. Скорость лодки изменяет прыжок мальчика. До прыжка двига-лись лодка и мальчик отдельно друг от друга. После прыжка мальчик и лодка двигались вместе.

Векторная сумма внешних сил (силы тяжести и силы реакции опоры) равна нулю, поэтому запишем закон сохранения импульса

1 способ (координатный). Так как тела движутся не вдоль одной прямой, то необходимо выбрать двухмерную систему координат, и тогда скорость лодки с мальчиком (направление которой неизвестно) будет равна

Направим ось OХ вдоль начальной скорости лодки, ось OY — вдоль начальной скорости мальчика, т.к. векторы скорости лодки и мальчика составляют прямой угол (рис. 5, а). Запишем уравнение (1) в проекциях на оси:

После подстановки уравнений (3) и (4) в (2) получаем:

Направление скорости υ определим следующим образом (рис. 5, б):

Примечание. Угол α можно было определить и через другие формулы

2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 5, в). Модуль скорости υ после прыжка найдем по теореме Пифагора

Направление скорости υ определим следующим образом (см. рис. 5, в):

 

к оглавлению ▴

Задача 4.

Летящий снаряд разрывается на два осколка, при этом первый осколок летит со скоростью 50 м/с под углом 90° по отношению к направлению движения снаряда, а второй — со скоростью 200 м/с под углом 30°. Найдите отношение массы первого осколка к массе второго осколка.

Скорость снаряда изменяет взрыв. До взрыва двигался только снаряд. После взрыва осколки снаряда двигались отдельно друг от друга.

Внешних сил нет, поэтому запишем закон сохранения импульса

1 способ (координатный). Направим ось OХ вдоль начальной скорости снаряда, ось OY — вдоль конечной скорости первого осколка (рис. 6, а). Запишем уравнение (1) в проекции на ось:

2 способ (векторный). Построим треугольник импульсов по уравнению (1) (рис. 6, б). Тогда из прямоугольного треугольника получаем

Автор Сакович А.Л.

Изначально импульс системы был равен p1 = M v, где M = m1 + m2. после импульс системы будет складываться из векторов m1 u1 и m2 u2. складывая их по правилу параллелограмма, нетрудно получить через теорему косинусов, что

M² v² = m1² u1² + m2² u2² — 2 m1u1 m2u2 cos (π — α)

cos (π — α) = — cosα

cosα = (M²v² — m1²u1² — m2²u2²) / (2 m1m2 u1u2)

cosα = (62^ (2) * 750^ (2) — 45^ (2) * 710^ (2) — 17^ (2) * 900^ (2)) / (2*45*17*710*900)

cos α ≈ 0.928

α = arccos (0.928) ≈ 21° 12′