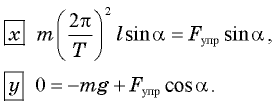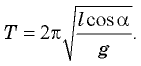На груз действуют две силы: сила тяжести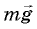 
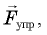
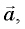
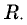
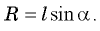
и сила натяжения нити 
направленная под углом ( к вертикали (рис. 15.4). Поскольку груз движется по окружности, равнодействующая этих сил обеспечивает центростремительное ускорение 
направленное к центру окружности. Радиус окружности обозначим 
Он связан с длиной нити и углом ее отклонения от вертикали соотношением 
Согласно второму закону Ньютона,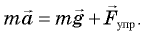 
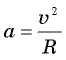
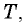
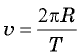
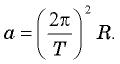
Центростремительное ускорение связано со скоростью соотношением 
(см. § 4. Криволинейное движение). Поскольку нас интересует период обращения 
выразим центростремительное ускорение через период, воспользовавшись соотношением 
(за время, равное одному периоду, груз совершает один полный оборот). Мы получим 
Запишем уравнение второго закона Ньютона в проекциях на оси координат. Совместим начало координат с положением груза в данный момент, ось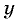 
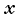
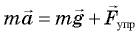
направим вертикально вверх, а ось 
— горизонтально вдоль радиуса к центру окружности. Из уравнения 
мы получим систему двух уравнений:
Из второго уравнения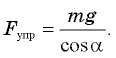 
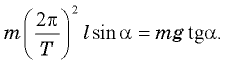
Подставляя это выражение в первое уравнение системы, получаем 
Отсюда 
Заметим, что если угол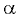 
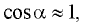
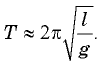
достаточно мал, можно принять 
и тогда получим 
В дальнейшем (см. § 20. Механические колебания) мы увидим, что таков же и период малых колебаний груза, подвешенного на нити.
Механика.
2014
УДК 531.01
DOI: 10.24412/2071-6168-2021-11-247-250
ОПРЕДЕЛЕНИЕ КРИТЕРИЕВ УСТОЙЧИВОСТИ ДВИЖЕНИЯ КОНИЧЕСКОГО МАЯТНИКА
Л.П. Семенова, О.А. Ткач
Рассматривается задача о движении конического маятника и определяются углы отклонения нити маятника от вертикального положения при которых сохраняется устойчивость движения конического маятника.
Ключевые слова: конический маятник, критерии устойчивости, теорема Рауса, теорема Ляпунова.
Рассматривается движение маятника массой m в сферических координатах 0, Г с длиной подвеса l (рисунок).
У л
г mg
Расчетная схема
Исследование удобно проводить в сферических координатах у, 6, r, которые связаны с декартовыми следующими соотношениями [1]:
х = r sin 6 cos у; y = r sin 6 sin у; z = r cos 6. Кинетическая энергия точки в сферических координатах определяется формулой
(1)
T — m — 2
r 2é2+(r2 sin2 eL2 + r2
а потенциальная энергия:
П = -mgr cos 0. (2)
Полагая, что для конического маятника углы 0 и у являются свободными переменными, а r = l = const — длина подвеса, формулы (1) и (2) принимают вид:
ml2 /л 2
2
T —e2 +jz2 sin2 e , а П — -mglcose.
(3)
Причем, координата у является циклической, а 9 — позиционной.
Исследуем устойчивость движения конического маятника с помощью функции Рауса [2]. Для циклического интеграла
С
(4)
— = ш^ът1 9 = С, т.е. у =-
ш12ът2 9 Подставим у в формулу (3) и получим:
т = ш191 +—с1—
1 1ш12ът2 9
Система уравнений Лагранжа при наличии циклических координат может быть сведена к уравнениям Рауса, где Я — функция Рауса, которая определяется соотношением:
147
Известия ТулГУ. Технические науки. 2021. Вып. 11
В нашем случае:
R = т-Iqq i =i
R = T — су = ^ é2 -2
С2
2ml2 sin2 é
откуда слагаемые для функции R определяются соотношениями:
R2 =
mi2 2
é; Ri = 0; R0 = —
C2
2mi2 sin2 é
Введем критерий устойчивости Рауса: необходимым условием устойчивости стационарного движения является наличие минимума функции:
W = П -Ro = -mgi cos é +
С2
2mi2 sin2 é
(5)
Константу С определим из состояния покоя функции W :
f dW Л
ддР
= 0′ т е. mgi sin é =
С 2 cos é
mi
2
С помощью циклического интеграла (5) исключим константу С. Функция Ж при 9 = а имеет минимум, т.к.
dW
dé
= 0;
d 2W
е=а
dé
2
= mgi cos é +
С2 (з cos2 é + sin2 é)
é=a
mi2 sin4 а
> 0.
Следовательно условие (6) выполняется, если
л П
0 <а < —.
(6)
(7)
Таким образом, применение теоремы Рауса показывает, что при выполнении условия (7) движение конического маятника устойчиво.
Проверку полученных результатов проведем по теореме Ляпунова [3], которая оценивает устойчивость движения с помощью знакоопределенной функции V, а точнее по ее производной. Предположим, что маятник вращается с постоянной угловой скоростью |/ 0 = ш, а начальное отклонение его é0 = а. Это движение будем считать невозмущенным. Как известно [3], параметры |/ 0, é0, а связаны соотношением
2
ш i cos а = g. (8)
Рассмотрим возмущенное движение маятника, т.е. предположим, что
é = а + xi, é = X2, у = Ш3 + X3. Формулы (1) и (2) показывают, что координата у является циклической, т.к. не входит в функцию Лагранжа L = T — П, поэтому характер движения не зависит от угла у. В задаче можно указать два интеграла движения: закон сохранения механической энергии
FХ2, Х3) = x^ +(ш + Х3)2 sin2(а + xi)]-mgicos( + xi) = Ci (9)
и закон сохранения момента количества движения относительно оси z
F2 (i, Х2, Х3 ) = mi2 (ш + X3 )sin2 (а + xi ) = С2. Полагая, что Ai = i, A 2 = A, Xi = X 2 = 0, составим функцию Ляпунова:
mi2 2 , / , 2 • 2/
V(xi, x2, x3 ) = —— x2 + (со + x3 ) sin (а + xi) — mgi cos( + xi) —
^ mi2 2-2 , ^
-ш sin а- mgi cos а
+ Ami
(ш + x3 )sin2 (а + xi) — ш
sin а
Разлагая функции cos(a + x,) и sin2(а + x,) в ряды и сохраняя малые члены до второго порядка, присоединив формулу (8) получим:
V(xb x2, x3) = xi<a(co + X)ml2 sin2a + x3(со + X)ml2 sin2 2a +
ml 2 / 2 2 2^^ 2 • 2
+ —— ^2 + x, ш cos 2a + 2x^q sin 2a + x3 sin aj+
x, 22 2 2¡ 2 ^
+ me l cos a + Xml x ш cos 2a + x^3 sin 2a j
при X = —ш линейные члены для величин x, и x3 пропадают и функция V принимает вид:
ttí 2 mc2l2 . 2 2 ml2 2 ml2 .2 л0)
V(1, x2, x3 ) = x,—2—sin a + x2 —— + x^ —^sin a, (10)
т.е. функция V является определенно положительной, и по теореме Ляпунова наблюдается устойчивое движение. Необходимо добавить, что при разложении в ряд функции cos(a + x,)
я
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
следует предположить, что 0 < a < —, что подтверждает условие устойчивости, полученное с
2
использованием функции Рауса.
Список литературы.
1. Лойцянский Л.Г., Лурье А.И. Курс теоретической механики: том II. М.: Наука, 1983.
637 с.
2. Меркин Д.Р. Введение в теорию устойчивости движения. М.: Наука, 1976. 319 с.
3. Ляпунов А.М. Общая задача об устойчивости движения. М.: Наука, 1950. 471 с.
Семенова Людмила Петровна, канд. техн. наук, доцент, ludmilacemenova@yandex.ru , Россия, Тула, Тульский государственный университет,
Ткач Ольга Александровна, канд. техн. наук, доцент, tkachoa@mail.ru, Россия, Тула, Тульский государственный университет
DETERMINATION OF CONICAL PENDULUM MOVEMENT STABILITY CRITERIA
L.P. Semenova, O.A. Tkach
The conical pendulum movement problem is considered. The angles of pendulum thread deviation from the vertical position are determined at which the conical pendulum movement stability is maintained.
Key words: conical pendulum, stability criteria, Rouse’s theorem, Lyapunov’s theorem.
Ludmila Petrovna Semenova, candidate of technical sciences, docent, ludmilacemeno-va@yandex.ru, Russia, Tula, Tula State University,
Tkach Olga Aleksandrovna, candidate of technical sciences, docent, tkachoa@mail.ru, Russia, Tula, Tula State University
Конический маятник описывая окружность радиусом 15 см делает 10 оборотов за 7, 7 секунд.
Каков угол отклонения маятника от вертикали?
На странице вопроса Конический маятник описывая окружность радиусом 15 см делает 10 оборотов за 7, 7 секунд? из категории Физика вы найдете
ответ для уровня учащихся 5 — 9 классов. Если полученный ответ не
устраивает и нужно расшить круг поиска, используйте удобную поисковую
систему сайта. Можно также ознакомиться с похожими вопросами и ответами
других пользователей в этой же категории или создать новый вопрос. Возможно,
вам будет полезной информация, оставленная пользователями в комментариях, где
можно обсудить тему с помощью обратной связи.
Опишем
движение небольшого бруска массой m,
расположенного на гладкой горизонтальной
поверхности и прикрепленного к
неподвижному упору с помощью легкой
пружины жесткости k.
Рис.4.1.
Пружинный маятник
Положение
бруска будем описывать с помощью
декартовой координаты x,
начало отсчета которой совместим с
положением, в котором пружина не
деформирована. При отклонении бруска
от положения равновесия на него будет
действовать сила упругости пружины F,
направленная к положению равновесия,
ее модуль определяется законом Гука: F
=- kx.
На основании второго закона Ньютона и,
пренебрегая трением, запишем уравнение,
описывающее движение бруска:
,
или
после преобразований:
Решение
этого уравнения имеет вид:
где
— циклическая частота собственных
колебаний. Частота собственных колебаний
не
зависит от их амплитуды при малой
амплитуде (пока выполняется линейный
закон Гука).
Период
колебаний бруска равен
Полученные
формулы для частоты и периода колебаний
легко объяснимы: частота колебаний
возрастает с ростом жесткости пружины
и убывает при возрастании массы груза.
Колебания,
возникающие под действием внутренних
возвращающих консервативных сил,
называются свободными.
Рассмотрим
теперь описание движения небольшого
шарика массой m,
подвешенного на легкой пружине жесткостью
k
(рис.).
Рис.
4.2. Вертикальный пружинный маятник
Направим
ось Ox
вертикально вниз, начало отсчета
совместим с положением недеформированной
пружины. В процессе движения на шарик
действуют сила тяжести mg
и
сила упругости Fупр,
модуль
которой определяется законом Гука Fупр
=- kx.
Уравнение второго закона Ньютона в
проекции на введенную ось имеет вид
Так
как сила упругости зависит от координаты
шарика (следовательно, не постоянна),
то движение шарика не будет равноускоренным.
Преобразуем уравнение (7)
Появившаяся
в уравнении величина 
имеет наглядный смысл: она указывает
положение равновесия шарика, в котором
сила тяжести уравновешивается силой
упругости 
.
Теперь можно сместить начало отсчета
оси координат, совместив его с положением
равновесия. В этой измененной системе
отсчета координата шарика равна 
,
ускорение шарика и в новой системе
отсчета остается прежним 
.
Поэтому уравнение движения шарика в
этой системе отсчета имеет вид, полностью
совпадающий с уравнением гармонических
колебаний
с
частотой
.Таким
образом, постоянная сила, действующая
в колебательной системе, не изменяет
частоты колебания, а только смещает
положение равновесия.
Полное решение уравнения движения (9)
нам известно, поэтому можно также
записать и полное решение уравнения
(7) в исходной системе отсчета
в
котором произвольные постоянные A, B
определяются из начальных условий.
Математический
маятник.
(http://www.all-fizika.com/virtual/mayatnik.php
http://physflash.narod.ru/Search/mechanics/25.htm
).
Небольшой
шарик, подвешенный на легкой нерастяжимой
нити, способен совершать свободное
колебательное движение (рис.).
Для
описания движения маятника будем считать
шарик материальной точкой, пренебрежем
массой нити и сопротивлением воздуха.
Такая модель называется математическим
маятником.
Рис.4.3.
Математический маятник
В
качестве координаты, описывающей
положение шарика, выберем угол отклонения
нити от вертикали
.
Для описания изменения этой координаты
удобно использовать основное уравнение
динамики вращательного движения
где
− момент инерции системы,
− угловое ускорение тела (вторая
производная от угла поворота),
− суммарный момент внешних сил действующих
насистему.
На шарик действуют силы тяжести mg и
натяжения нити. Момент силы натяжения
нити
относительно точки подвеса равен нулю,
поэтому уравнение (1) для подвешенного
шарика приобретает вид:
или
Это
уравнение описывает колебания маятника,
но не является уравнением гармонических
колебаний. Однако, если считать углы
отклонения малыми (
<100
), можно воспользоваться приближенной
формулой
в этом приближении уравнение превращается
в уравнение гармонических колебаний
где
− круговая частота малых колебаниймаятника.
Решение этого уравнения ищется в виде
здесь
− максимальное отклонение нити, то есть
амплитуда колебаний. Для простоты будем
считать, что начальная скорость шарика
равна нулю.
Период малых колебаний
маятника выражается через круговую
частоту
Так
как малые колебания математического
маятника являются гармоническими, то
их период не зависят от амплитуды. Этот
факт был экспериментально отмечен еще
Г. Галилеем. Отметим, что период колебаний
математического маятника не зависит
также от массы шарика.
Формула (6)
может быть использована и используется
для экспериментального определения
ускорения свободного падения. Длина
нити и период колебаний достаточно
просто измерить экспериментально, затем
с помощью формулы (6) можно рассчитать
ускорение свободного падения.
Математический
маятник с пружиной.
Рассмотрим
еще один пример колебательной системы,
являющейся «гибридом» математического
и пружинного маятника (рис.4.4):
Рис.
4.4. Математический маятник с пружиной
к
шарику, подвешенному на нити длиной l,
прикреплена легкая пружина так, что в
положении равновесия нить маятника
располагается вертикально (в этом случае
пружина не деформирована). По-прежнему,
положение маятника будем описывать с
помощью угла отклонения
,
который будем считать малым. Уравнение
динамики вращательного движения
относительно точки подвеса для шарика
будет иметь вид
где
− момент инерции маятника, − угловое
ускорение,
− момент силы тяжести,
− момент силы упругости. Считая угол
отклонения малым, удлинение пружины
можно представить в виде
и
при этом можно считать, что ось пружины
все время остается горизонтальной. В
этом же приближении можно положить л,
.
Поэтому уравнение (1) упрощается
или
Это
уравнение является уравнением
гармонических колебаний: ускорение
пропорционально смещения от положения
равновесия. Круговая частота этих
колебаний равна
Физический
маятник (http://physflash.narod.ru/Search/mechanics/25.htm)
Физическим
маятником называется твердое тело,
закрепленное на неподвижной горизонтальной
ocи (оси подвеса), не проходящей через
центр тяжести, и совершающее колебания
относительно этой оси под действием
силы тяжести. В отличие от математического
маятника массу такого тела нельзя
считать точечной.
Рис.
4.5. Физический маятник
При
небольших углах отклонения
(рис. 7.4) физический маятник так же
совершает гармонические колебания.
Будем считать, что вес физического
маятника приложен к его центру тяжести
в точке С. Силой, которая возвращает
маятник в положение равновесия, в данном
случае будет составляющая силы тяжести
– сила F.
Знак
минус в правой части означает то, что
сила F направлена в сторону уменьшения
угла
.
С учетом малости угла α
Для
вывода закона движения математического
и физического маятников используем
основное уравнение динамики вращательного
движения
.
Момент силы: определить в явном виде
нельзя. С учетом всех величин, входящих
в исходное дифференциальное уравнение
колебаний физического маятника имеет
вид:
или
где
Решением
этого уравнения является функция
Где
—
начальная фаза колебаний
Определим
длину
l
математического, при которой период
его колебаний равен периоду колебаний
физического маятника, т.е.
или
.
Из
этого соотношения определяем:
Данная
формула определяетприведенную
длину физического маятника
,
т.е. длину такого математического
маятника, период колебаний которого
равен периоду колебаний данного
физического маятника.
Конический
маятник.
В
коническом маятнике (рис.4.6) тело маятника
(небольшое по размерам тело) вращается
в горизонтальной плоскости. Угол,
образуемый нитью подвеса с вертикалью,
проведенной через точку подвеса, остается
неизменным. Уравнение описывающее
движение маятника имеет вид:
В
проекциях на оси:
Рис.4.6.
Конический маятник
отсюда
.
С другой стороны
.Отсюда
получаем:
.
Для
малых углов конуса
;
тогда период колебаний конического
маятника
.
Крути́льный
ма́ятник (также
торсио́нный
ма́ятник,
враща́тельный
ма́ятник)
— механическая
система, представляющая собой тело,
подвешенное в поле тяжести на тонкой
нити и обладающее лишь однойстепенью
свободы: вращением вокруг оси,
задаваемой неподвижной нитью.
Рис.
4.7. Крутильный маятник
Если
при повороте тела в нити возникает
момент сил, пропорциональный углу
поворота, то тело будет вращаться по
гармоническому закону с периодом
,
где
J—
момент
инерциитела, а
k —
вращательный коэффициент
жёсткостимаятника. Крутильный маятник
представляет собой очень чувствительный
механический прибор. Именно с помощью
крутильного маятника изучается, например,гравитационное
взаимодействиемассивных тел в
лаборатории и проверяетсязакон
всемирного тяготенияна субмиллиметровом
масштабе.
Крутильным
маятником является баланс — деталь
балансирного механизма механических
часов, вращательные колебания которой
определяют точность их хода. В2005 годубыло опубликовано сообщение о создании
крутильного маятника на одной молекуле —
одностеннойуглеродной
нанотрубке(J. C. Meyer,
M. Paillet and S. Roth, Science, 309, 1539 (2 September
2005)).
Существует
много разновидностей механических
колебательных систем, в которых
используются силы упругих деформаций.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Конический маятник
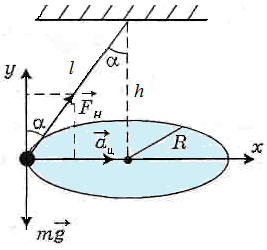
Подвешенный на нити груз, который равномерно движется по окружности в горизонтальной плоскости, называют коническим маятником (рис. 21.6).
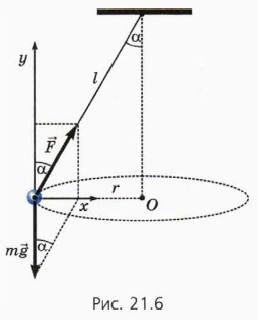
На груз действуют сила тяжести m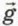 
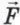
и сила натяжения 1 нити 
, направленная вдоль нити. Равнодействующая этих сил вызывает центростремительное ускорение груза.
1 Силу натяжения нити в данном случае неудобно обозначать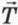 
, потому что буквой Т обозначен период обращения груза по окружности.
r — радиус окружности,
α — угол между нитью и вертикалью, Т — период обращения груза по окружности.
7. Используя рисунок 21.6, объясните смысл следующих уравнений:
П о д с к а з к а. Воспользуйтесь тем, что r = lcos α.
8. Чему равен период обращения конического маятника, если длина нити равна l?
9. Шарик массой 100 г, подвешенный на нити длиной 50 см, вращается по окружности в горизонтальной плоскости. При этом сила натяжения нити 2 Н.
а) Какой угол составляет нить с вертикалью?
б) Чему равен период обращения шарика по окружности?
в) Чему равен радиус окружности, по которой движется шарик?
г) С какой скоростью движется шарик?
д) Во сколько раз ускорение шарика больше ускорения свободного падения?
е) За какое время шарик пройдёт путь, равный 1 км?
Источник
Лабораторная работа «Изучение движения тел по окружности под действием силы тяжести и упругости»
Ищем педагогов в команду «Инфоурок»
Лабораторная работа №1.
Изучение движения тел по окружности под действием силы тяжести и упругости .
Цель работы : определить центростремительное ускорение шарика при его равномерном движении по окружности.
Оборудование: штатив с муфтой и лапкой, лента измерительная, циркуль, динамометр лабораторный, весы с разновесами, шарик на нити, лист бумаги, линейка, пробка.
1. Какие две силы действуют на конический маятник?
2. Равнодействующая этих сил сообщает маятнику…?
3. Модуль данного ускорения можно определить по формуле…?
1. Определите массу шарика.
2. Шарик, подвешенный на нити, закрепите в лапке штатива.
3. Вычертите на листе бумаги окружность радиусом 20 см.
4. Штатив с маятником расположите так, чтобы продолжение нити проходило через центр окружности.
5. Взяв нить пальцами у точки подвеса, приведите маятник во вращательное движение над листом бумаги так, чтобы шарик описывал такую же окружность, как и начерченная на бумаге.
6. Измерьте время 20 полных оборотов маятника.
7. Рассчитайте период обращения маятника по формуле: T = t ср ./N
8. Рассчитайте значение центростремительного ускорения: а 1 = 4π 2 R/ T 2
9. Определите высоту маятника. Для этого измерьте расстояние по вертикали от центра шарика до точки подвеса.
10. Рассчитайте значение ускорения по формуле: а 2 = g R/ h.
11. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль равнодействующей силы
12. Оттяните горизонтально расположенным динамометром шарик на расстояние, равное радиусу окружности, и измерьте модуль равнодействующей силы, которая равна силе упругости при растяжении пружины.
13. Используя второй закон Ньютона, рассчитайте значение центростремительного ускорения: а 3 = F/m.
14. Результаты измерений и вычислений занесите в таблицу.
1. Почему при выполнении работы определяли время, за которое совершается небольшое число оборотов?
2. Определите линейную скорость тела по результатам опытов.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс профессиональной переподготовки
Физика: теория и методика преподавания в образовательной организации
Курс повышения квалификации
Современные педтехнологии в деятельности учителя
Номер материала: ДВ-391301
Международная дистанционная олимпиада Осень 2021
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Минтруд предложил проект по реабилитации детей-инвалидов
Время чтения: 1 минута
Google сможет удалять снимки с детьми из результатов поиска по запросу
Время чтения: 1 минута
Около половины детей болеют коронавирусом в бессимптомной форме
Время чтения: 1 минута
Российские педагоги чаще всего жалуются на излишнюю отчетность и низкую зарплату
Время чтения: 2 минуты
Рособрнадзор открыл горячую линию по вопросам контрольных в школах
Время чтения: 1 минута
Прослушивание музыки снижает усталость мозга
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Источник
СОДЕРЖАНИЕ
Использует
Одно из наиболее важных применений конического маятника было в регуляторе флайбола ( центробежном регуляторе ), изобретенном Джеймсом Ваттом в 1788 году, который регулировал скорость паровых двигателей в эпоху пара в 1800-х годах. В тезерболе для игр на игровой площадке используется мяч, прикрепленный к шесту шнуром, который функционирует как конический маятник, хотя маятник становится короче, когда шнур наматывается на шест. Некоторые аттракционы действуют как конические маятники.
Анализ
Рассмотрим конический маятник, состоящий из боба массы m, вращающегося без трения по окружности с постоянной скоростью v на струне длиной L под углом θ к вертикали.
На боб действуют две силы:
Т грех θ знак равно м v 2 р < Displaystyle Т грех тета = < гидроразрыва > > ,> 
Поскольку в вертикальном направлении ускорение отсутствует, вертикальная составляющая натяжения струны равна и противоположна весу боба:
Эти два уравнения можно решить для T / m и приравнять, тем самым исключив T и m :
Поскольку скорость маятникового боба постоянна, ее можно выразить как длину окружности 2 πr, деленную на время t, необходимое для одного оборота боба:
Подставляя правую часть этого уравнения для v в предыдущее уравнение, мы находим:
Подстановка этого значения на r дает формулу, единственным изменяющимся параметром которой является угол подвеса θ :
Для малых углов θ cos ( θ ) ≈ 1; в таком случае
Источник
Решебник по физике за 9 класс Кикоин: решения задач, самое важное и лабораторные работы
Лабораторная работа № 5 «Изучение движения тела по окружности под действием сил упругости и тяжести».
Цель работы: убедиться в том, что при движении тела по окружности под действием нескольких сил их равнодействующая равна произведению массы тела на ускорение: F= ma. Для этого используется конический маятник (рис. 178, а).
На прикрепленное к нити тело (им в работе является груз из
набора по механике) действуют сила тяжести F1 и сила упругости F2. Их равнодействующая равна
Сила F и сообщает грузу центростремительное ускорение
Для нахождения периода удобно измерить время t определенного числа N оборотов. Тогда Т =
Модуль равнодействующей F сил F1 и F2 можно измерить, скомпенсировав ее силой упругости Fупр пружины динамометра так, как это показано на рисунке 178, б.
Согласно второму закону Ньютона,
это равенство полученных в опыте значений Fynp, m и а может оказаться, что левая часть этого равенства отличается от единицы. Это и позволяет оценить погрешность эксперимента.
Средства измерения: 1) линейка с миллиметровыми делениями; 2) часы с секундной стрелкой; 3) динамометр.
Материалы: 1) штатив с муфтой и кольцом; 2) прочная нить; 3) лист бумаги с начерченной окружностью радиусом 15 см; 4) груз из набора по механике.
Порядок выполнения работы
1. Нить длиной около 45 см привяжите к грузу и подвесьте к кольцу штатива.
2. Одному из учащихся взяться двумя пальцами за нить у точки подвеса и привести во вращение маятник.
3. Второму учащемуся измерить лентой радиус r окружности, по которой движется груз. (Окружность можно начертить заранее на бумаге и по этой окружности привести в движение маятник.)
4. Определите период Т обращения маятника при помощи, часов с секундной стрелкой.
Для этого учащийся, вращающий маятник, в такт с его оборотами произносит вслух: нуль, нуль и т. д. Второй учащийся с часами в руках, уловив по секундной стрелке удобный момент для начала отсчета, произносит: «нуль», после чего первый вслух считает число оборотов. Отсчитав 30—40 оборотов, фиксирует промежуток времени t. Опыт повторяют пять раз.
5. Рассчитайте среднее значение ускорения по формуле (1), учитывая, что с относительной погрешностью не более 0,015 можно считать π 2 = 10.
6. Измерьте модуль равнодействующей F, уравновесив ее силой упругости пружины динамометра (см. рис. 178, б).
7. Результаты измерений занесите в таблицу:
опыта t, с tср,с N m, кг r,
8. Сравните отношение
с единицей и сделайте вывод о погрешности экспериментальной проверки того, что центростремительное ускорение сообщает телу векторная сумма действующих на него сил.
Груз из набора по механике, подвешенный на закрепленную в верхней точке нить, движется в горизонтальной плоскости по окружности радиуса r под действием двух сил:
и силы упругости N.
Равнодействующая этих двух сил F направлена горизонтально к центру окружности и сообщает грузу центростремительное ускорение.
Т — период обращения груза по окружности. Его можно вычислить подсчитав время, за которое груз совершает некоторое число полных оборотов
Центростремительное ускорение рассчитаем по формуле
Теперь, если взять динамометр и прикрепить его к грузу, как показано на рисунке, можно определить силу F (равнодействующую сил mg и N.
с единицей. Для того, чтобы радиус окружности, по которой движется груз, изменялся вследствие влияния сопротивления воздуха медленнее и изменение это незначительно влияло на измерения, следует выбирать его небольшим (порядок 0,05
| № опыта | t, с | tср, с | n | m, кг | r, м | а, м/с 2 | F, H |
Оценка погрешностей. Точность измерения: линейка —
Подсчитаем погрешность определения периода (если считать, что число n определено точно):
Погрешность определения ускорения подсчитаем как:
Погрешность определения ma
С другой стороны, силу F мы измерили со следующей погрешностью:
Такая погрешность измерения, конечно, очень велика. Измерения с такими погрешностями годны только для приблизительных оценок. Отсюда видно, что отклонение отношение
1 * Так что вам не следует смущаться, если в этой лабораторной работе отношение
будет отличным от единицы. Просто аккуратно оцените все погрешности измерений и сделайте соответствующий вывод.
Шаблоны Инстаграм БЕСПЛАТНО
Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?
Напишите моему чат-помощнику в Telegram ниже ?
Вы получите: ? Бесплатные шаблоны «Bezh», «Akvarel», «Gold»
или пишите «Хочу бесплатные шаблоны» в директ Инстаграм @shablonoved.ru
Шаблоны Инстаграм БЕСПЛАТНО
Хотите получить БЕСПЛАТНЫЙ набор шаблонов для красивого Инстаграма?
Напишите моему чат-помощнику в Telegram ниже ?
Вы получите: ? Бесплатные шаблоны «Bezh», «Akvarel», «Gold»
Источник
Цель: убедиться в том, что при движении тела по окружности под действием нескольких сил их равнодействующая равна произведению массы тела на ускорение F = ma (на примере конического маятника).
Оборудование: 1) динамометр; 2) часы с секундной стрелкой или секундомер; 3) линейка измерительная; 4) груз из набора по механике массой 100 г; 5) штатив лабораторный с кольцом; 6) прочная нить; 7) лист бумаги с начерченной на нем окружностью радиусом 15-20 см; 
транспортир.
Таким образом, в работе необходимо сравнить силу F с произведением 
Для выполнения работы собирают установку с коническим маятником. К концу штатива подвешивают на нити груз. Для этого верхний конец нити продевают в отверстие кольца штатива и заклинивают заостренной спичкой.
На столе под маятником располагают лист бумаги с начерченной на нем окружностью. Центр окружности располагают на отвесной линии, проходящей через точку подвеса маятника. Затем маятник приводят во вращательное движение в горизонтальной плоскости, взявшись двумя пальцами за нить у точки подвеса. Радиус вращения маятника подбирают равным радиусу окружности.
Подставляют полученные данные (R, m, Т) в приведенную выше формулу и находят величину mа.
Равнодействующую сил тяжести и упругости можно найти несколькими способами, например:
2. Измерением силы F c помощью динамометра. В этом случае маятник оттягивают от положения равновесия на расстояние, равное радиусу окружности R, и снимают показания динамометра. Последний способ измерения силы дает наименьшую погрешность, так как в этом случае она определяется только погрешностями динамометра и отсчета.
Сопоставляя результаты измерения F и mа, убеждаются, что они близки между собой. Относительную погрешность косвенного измерения силы выявляют на основе соотношения 
Находят по формуле 
При малых углах отклонения маятника можно считать, что еR = 0, так как период его не зависит от угла отклонения. При достаточно длинной нити можно уменьшить есист. до такого значения, что суммой (есист. + еm) можно пренебречь по сравнению со случайной погрешностью 
(формула, которая вносит основной вклад в погрешность). Поэтому 
В зависимости от числа опытов по вычисленному значению произведения та находят границы абсолютной погрешности ΔF = еF(mа)
Библиотека образовательных материалов для студентов, учителей, учеников и их родителей.
Наш сайт не претендует на авторство размещенных материалов. Мы только конвертируем в удобный формат материалы из сети Интернет, которые находятся в открытом доступе и присланные нашими посетителями.
Если вы являетесь обладателем авторского права на любой размещенный у нас материал и намерены удалить его или получить ссылки на место коммерческого размещения материалов, обратитесь для согласования к администратору сайта.
Разрешается копировать материалы с обязательной гипертекстовой ссылкой на сайт, будьте благодарными мы затратили много усилий чтобы привести информацию в удобный вид.
© 2014-2021 Все права на дизайн сайта принадлежат С.Є.А.
Источник