2017-10-05
Под каким углом отскакивает футбольный мяч от стенки?
Решение:
рис.1
рис.2
рис.3
рис.4
рис.5
Задача, разумеется, тривиальная, если считать, что удар абсолютно упругий, а стенка и мяч идеально гладкие. Тогда трение между мячом и поверхностью стенки отсутствует и угол отражения $beta$ равен углу падения $alpha$ (рис. 1).
Совсем иначе обстоит дело, если мяч и стенка шероховатые, так что пренебрегать трением уже нельзя. Однако и в этом случае легко найти угол отражения, если известен коэффициент трения р мяча о поверхность стенки.
Будем рассуждать следующим образом. Разложим вектор скорости поступательного движения мяча до удара $vec{v}$ на две составляющие: $vec{v}_{perp}$, направленную перпендикулярно поверхности стенки, и $vec{v}_{ parallel}$ направленную вдоль поверхности (рис. 2). Обозначим соответствующие скорости мяча после отскока через $vec{v}_{ perp}^{ prime}$ и $vec{v}_{ parallel}^{ prime}$. Перпендикулярная составляющая скорости мяча при ударе о стенку меняет свое направление на противоположное, оставаясь неизменной по модулю. Параллельная же составляющая скорости, вообще говоря, изменяется по модулю.
Чтобы убедиться в этом, рассмотрим силы, действующие па мяч со стороны стенки при ударе (рис. 3). Направленная но нормали к стенке сила $vec{N}$ — это сила упругости, возникающая при деформации мяча. Деформацию хорошо накачанного мяча можно считать упругой, после удара мяч восстанавливает свою форму. Поэтому энергия упругой деформации мяча после удара снова перейдет в кинетическую энергию.
Другими словами, часть кинетической энергии мяча, связанная с его движением по нормали к стенке, остается неизменной.
Изменение составляющей скорости, параллельной поверхности, происходит под действием силы трения. Эта сила направлена в сторону, противоположную скорости точек поверхности мяча в месте соприкосновения со стенкой. Если мяч до удара не вращался, то скорости этих точек равны $vec{v}_{ parallel}$, и действие силы трения приводит к уменьшению модуля $vec{v}_{ parallel}$. Это значит, что угол отражения $beta$ меньше угла падения $alpha$. Именно этот случай и изображен на рис. 1 и 2. Сила трения может и увеличивать значение $v_{ parallel}$, если до удара о стенку мяч вращался в направлении, указанном на рис. 4. При достаточно быстром вращении мяча ( $omega R > v_{ parallel}$) касающиеся стенки точки мяча имеют скорости, направленные влево, сила трения направлена вправо и значение $v_{ parallel}$ возрастает. В этом случае угол отражения больше угла падения.
Рассмотрим подробно случай, когда мяч до удара не вращается. Будем также считать, что скорости точек мяча, касающихся стенки, не обращаются в нуль: в течение удара проскальзывание не прекращается. Сила $vec{N}$ (рис. 3) возникает в момент соприкосновения мяча со стенкой, затем растет, достигая наибольшего значения в момент максимальной деформации мяча, а затем убывает до нуля. Сила трения скольжения $vec{F}_{тр}$ в течение удара также не остается постоянной. В любой момент времени модули сил $vec{F}_{тр}$ и $ vec{N}$ связаны законом Кулона — Амонтона:
$F_{тр} = mu N$. (1)
Поэтому в течение всего удара полная сила $vec{Q}$, с которой поверхность стенки действует на мяч, изменяется по модулю, но остается неизменной по направлению, образуя угол $gamma$ с нормалью к стенке. Как видно из рис. 3, $tg gamma = mu$. Это позволяет найти угол отражения мяча $beta$.
На основании второго закона Ньютона изменение импульса мяча при ударе о стенку $Delta vec{p}$ совпадает по направлению с силой $vec{Q}$. С помощью рис. 2 построим вектор изменения импульса $Delta vec{p} = m( vec{v}^{ prime} — vec{v})$ (рис. 5). Этот вектор, так же как и вектор $vec{Q}$ на рис. 3, образует угол $gamma$ с нормалью к стенке. Непосредственно из рис. 5 видно, что
$v_{ parallel}^{ prime} = v_{ parallel} — 2v_{ perp} tg gamma$. (2)
Деля обе части этого равенства на $v_{ perp}$ и учитывая, что $v_{ parallel}/v_{ perp} = tg alpha, v_{ parallel}^{ prime}/ v_{ perp}^{ prime} = tg beta$, a $tg gamma = mu$, получаем
$tg beta = tg alpha — 2 mu$. (3)
Из полученной формулы видно, что при малых углах падения, когда $tg alpha < 2 mu$, результат теряет смысл. С чем это связано? Формула (3) выведена в предположении, что проскальзывание мяча не прекращалось в течение всего времени его контакта со стенкой. Однако при малых углах падения проскальзывание мяча может прекратиться раньше, чем он отделится от стенки. Это связано с тем, что сила трения скольжения, направленная противоположно $vec{v}_{ parallel}$, не только тормозит поступательное движение мяча, но и вызывает его вращение по часовой стрелке, так как точка приложения силы трения не совпадает с центром мяча. Проскальзывание прекращается в тот момент, когда связанная с вращением скорость нижней точки мяча сравняется по модулю с параллельной поверхности составляющей скорости центра мяча.
Случай, когда в процессе столкновения со стенкой проскальзывание мяча прекращается, более сложен для исследования, так как требует привлечения уравнения, описывающего вращательное движение. При этом оказывается, что ответ, даваемый формулой (3), становится неприменимым даже при угле падения $alpha$, тангенс которого несколько больше $2 mu$. Точный расчет дает для предельного угла падения $tg alpha = 5 mu$.
Отскочивший от шероховатой стенки мяч обязательно будет вращаться, даже если до удара он не вращался. Кинетическая энергия этого вращения возникает за счет уменьшения кинетической энергии поступательного движения. Некоторая часть механической энергии мяча при ударе переходит в тепло.
Нетрудно сообразить, что даваемое формулой (3) значение угла отражения $beta$ справедливо и в том случае, когда до удара мяч вращался против часовой стрелки. Не представляет труда найти угол отражения и тогда, когда до удара мяч вращался по часовой стрелке. Если это вращение достаточно быстрое, так что проскальзывание мяча не прекращается в течение удара, то, рассуждая так же, как и при получении выражения (3), находим
$tg beta = tg alpha + 2 mu$. (4)
В этом случае кинетическая энергия поступательного движения мяча в результате удара о стенку увеличивается. Это увеличение, как и выделение тепла во время удара, происходит за счет кинетической энергии вращения.
1. Относительное движение брошенных тел
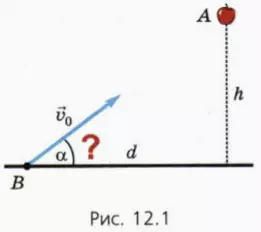
Пусть в некоторый момент (t = 0) из точки A на высоте h начинает падать яблоко (рис. 12.1). Лежащий на траве юный стрелок в тот же момент стреляет из пружинного пистолета, намереваясь попасть «в яблочко». Пистолет находится в точке B на расстоянии d от вертикали, вдоль которой падает яблоко, а скорость пули по модулю равна v0.
1) Под каким углом а к горизонту надо направить пулю?
2) В какой момент времени пуля попадет в яблоко?
Найдем сначала ответы на эти вопросы уже знакомым нам способом. Введем систему координат с началом в точке B, ось x направим по горизонтали вправо, а ось y – вверх. Запишем, как зависят от времени координаты пули и яблока, и учтем, что в момент попадания пули в яблоко их координаты совпадают.
? 1. Объясните, почему пуля может попасть в яблоко при условии, что
tg α = h/d. (1)
Эта удивительно простая формула утверждает, что целиться надо точно в яблочко – так, будто ни пуля, ни яблоко не чувствуют притяжения Земли! Для того чтобы пуля попала в яблоко, значение имеет (казалось бы) только направление ее начальной скорости.
? 2. Объясните, почему до попадания пули в яблоко они будут двигаться в течение времени
t = AB/v0. (2)
Здесь AB = √(d2 + h2) – расстояние между пулей и яблоком в начальный момент.
Подсказка. Воспользуйтесь тем, что t = d/v0x = d/(v0cos α).
Формула (2) тоже замечательна своей простотой: как будто бы яблоко и правда замерло на месте в ожидании пули, а пуля летела к яблоку, не чувствуя земного притяжения!
Найдем теперь физическую разгадку этой «простоты» и покажем, как можно было найти угол α и время полета устно.
Поскольку яблоко и пуля движутся с ускорением свободного падения 
Перейдем в систему отсчета, связанную с яблоком. Скорость яблока в этой системе отсчета остается равной нулю, а скорость пули относительно яблока
Итак, до попадания в яблоко пуля движется относительно яблока с постоянной скоростью 
Вот почему целиться надо «точно в яблочко», и вот почему время полета пули до попадания в яблоко равно начальному расстоянию между ними, деленному на начальную скорость пули! Мы видим, что полученные выше формулы (1), (2) можно было записать сразу, без вычислений.
Остается проверить: действительно ли модуль начальной скорости пули не имеет значения для попадания в яблоко?
? 3. При какой начальной скорости пули она может попасть в яблоко?
Подсказка. Время полета пули до попадания в яблоко должно быть меньше времени падения яблока на землю.
Докажем, что тела, брошенные под любыми углами к горизонту с любыми начальными скоростями, движутся друг относительно друга с постоянной (по модулю и по направлению) скоростью, то есть прямолинейно равномерно.
Действительно, пусть начальные скорости двух тел равны 

Скорость второго тела относительно первого
Эта формула показывает, что относительная скорость тел не зависит от времени, то есть тела движутся друг относительно друга с постоянной скоростью.
Свидетелями этого интересного явления мы становимся, наблюдая во время фейерверков за разноцветными огненными шарами (рис. 12.2).
Они имеют форму шаров именно потому, что образующие их светящиеся ракеты движутся друг относительно друга с постоянными скоростями! Знание «секрета» относительного движения брошенных тел позволяет легко решать задачи, кажущиеся на первый взгляд довольно трудными.
? 4. Из одной точки одновременно бросили два тела – первое под углом 15º к горизонту, а второе – под углом 75º к горизонту. Начальная скорость каждого тела 20 м/с. Траектории тел лежат в одной плоскости. Попробуйте на все следующие вопросы (кроме а) ответить устно.
а) Изобразите на одном чертеже начальные скорости тел и найдите начальную скорость второго тела относительно первого. Чему она равна по модулю?
б) Будет ли эта относительная скорость изменяться во время полета тел?
в) Какой формулой в единицах СИ выражается зависимость расстояния d между телами во время полета?
г) Через какой промежуток времени после броска расстояние между движущимися телами стало равным 10 м?
д) Объясните, почему эти тела не могут столкнуться в полете.
2. Отскок мяча от наклонной плоскости
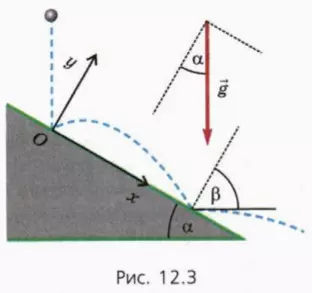
Мяч свободно падает без начальной скорости с высоты h на наклонную плоскость с углом наклона α, отскакивает от нее и затем снова ударяется о плоскость (рис. 12.3).
Будем считать, что в результате столкновения мяча с плоскостью модуль скорости мяча не изменяется, а угол отражения равен углу падения. (Углы падения и отражения – это углы между скоростью мяча и перпендикуляром к наклонной плоскости непосредственно перед ударом мяча о плоскость и после удара.)
Выясним:
1) чему равен промежуток времени τ между ударами?
2) чему равно расстояние d между точками ударов?
Обычно при рассмотрении ситуаций, в которых речь идет о наклонной плоскости, удобно направить ось x вдоль наклонной плоскости вниз, а ось y – перпендикулярно наклонной плоскости вверх (см. рис. 12.3).
Обозначим 

? 5. Объясните, почему зависимость проекций скорости мяча от времени между ударами задается уравнениями
vx = vx1 + gxt = (v0 + gt) sin α,
vy = vy1 + gyt = (v0 – gt) cos α.
? 6. Объясните, почему зависимость координат мяча от времени между ударами задается уравнениями
x = vx1t + gxt2/2 = (v0 + gt/2)t sin α;
y = vy1t + gyt2/2 = (v0 – gt/2)t cos α.
? 7. Получите формулу для промежутка времени τ между первым и вторым ударами мяча о плоскость:
τ = 2(v0/g).
Подсказка. Воспользуйтесь тем, что при ударе мяча о плоскость координата мяча y = 0.
Итак, промежуток времени между ударами не зависит от угла наклона плоскости α! Он определяется только модулем скорости в момент падения мяча, то есть начальной высотой h.
? 8. Выразите расстояние d между точками первых двух ударов мяча о плоскость через v0, α и g.
? 9. Объясните, почему расстояние между точками второго и третьего ударов мяча о плоскость равно 2d.
? 10.Расстояния между точками последовательных ударов мяча о плоскость относятся, как 1 : 2 : 3 : 4…. Объясните, как получается это отношение.
Найдем соотношение между углом наклона плоскости α и углом β отражения мяча после второго удара (рис. 12.3).
Для этого надо найти проекции скорости мяча сразу после второго удара о плоскость.
? 11.Объясните, почему проекции скорости мяча сразу после второго удара о плоскость выражаются формулами
vx = 3v0 sin α,
vy = v0 cos α.
Подсказка. Воспользуйтесь тем, что в результате удара о плоскость проекция скорости мяча на ось x не изменяется, а проекция скорости на ось y изменяет знак, а также формулами зависимости проекций скорости мяча от времени и выражением для промежутка времени τ между двумя ударами.
? 12. Обоснуйте формулу
tg β = 3tg α.
Подсказка. Воспользуйтесь тем, что сразу после второго удара
tg β = vx/vy.
? 13.Чему равен угол наклона плоскости α, если сразу после второго удара скорость мяча направлена горизонтально?
Подсказка. Воспользуйтесь тем, что в таком случае α + β = 90º, поэтому tg β = 1/tg α.
Дополнительные вопросы и задания
В задачах этого параграфа предполагается, что сопротивлением воздуха можно пренебречь.
14. С высоты 20 м одновременно бросили горизонтально в противоположных направлениях два камешка. Начальная скорость первого 10 м/с, а второго – 20 м/с. Чему , будет равно расстояние между камешками через 1 с; 2 с; 3 с?
15. Лежащий на земле футбольный мяч после удара приобрел скорость 10 м/с под углом 45º к горизонту и ударился о вертикальную стену, находящуюся на расстоянии 3 м от начальной точки. Траектория мяча лежит в плоскости, перпендикулярной стене. Считайте, что при ударе о стену горизонтальная проекция скорости мяча изменила знак, а модуль скорости не изменился.
а) В какой момент произошел удар мяча о стену: при его подъеме или при спуске?
б) На какой высоте мяч ударился о стену?
в) Чему была равна скорость мяча при ударе?
г) На каком расстоянии от стены упал бы мяч, если бы он пролетел сквозь стену, не изменив скорости?
д) На каком расстоянии от стены упал мяч после удара?
Решение.
Для нахождения модуля средней силы нормальной реакции со стороны стены необходимо найти изменения импульса тела. Импульс тела определим по формуле:
[ Delta vec{p}=mcdot {{vec{upsilon }}_{2}}-mcdot {{vec{upsilon }}_{1}}, Delta p=Fcdot tau , F=frac{Delta p}{tau } (1). ]
F = 110,0 Н
Покажем рисунок, учитываем, что при упругом ударе υ1 = υ2.
Определим угол α:
[ begin{align}
& Delta vec{p}=mcdot {{{vec{upsilon }}}_{2}}-mcdot {{{vec{upsilon }}}_{1}}, Delta p=sqrt{Delta p_{x}^{2}+Delta p_{y}^{2}}, \
& Delta {{p}_{y}}=mcdot {{upsilon }_{2}}cdot sin alpha -mcdot {{upsilon }_{1}}cdot sin alpha , Delta {{p}_{y}}=0. \
& Delta {{p}_{x}}=mcdot {{upsilon }_{2}}cdot cos alpha +mcdot {{upsilon }_{1}}cdot cos alpha , Delta {{p}_{x}}=2cdot mcdot {{upsilon }_{2}}cdot cos alpha . \
& Delta {{p}_{{}}}=2cdot mcdot {{upsilon }_{2}}cdot cos alpha , cos alpha =frac{Delta p}{2cdot mcdot {{upsilon }_{2}}}. \
end{align} ]
соsα = 0,088, α = 850.
Ответ: 110,0 Н, 850.
« Последнее редактирование: 07 Января 2015, 11:46 от alsak »
Записан
Когда тело бросают вверх под углом к горизонту, оно сначала равнозамедленно поднимается, а затем равноускорено падает. При этом оно перемещается относительно земли с постоянной скоростью.
Важные факты!График движения тела, брошенного под углом к горизонту:
α — угол, под которым было брошено тело
- Вектор скорости тела, брошенного под углом к горизонту, направлен по касательной к траектории его движения.
- Так как начальная скорость направлена не вдоль горизонтальной линии, обе ее проекции отличны от нуля. Проекция начальной скорости на ось ОХ равна v0x = v0cosα. Ее проекция на ось ОУ равна v0y = v0sinα.
- Проекция мгновенной скорости на ось ОХ равна: vx = v0 cosα. Ее проекция на ось ОУ равна нулю: vy = v0 sinα – gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Кинематические характеристики
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Минимальной скорости тело достигает в верхней точке траектории. Она выражается формулой:
vmin = v0 cosα = vh
Максимальной скоростью тело обладает в момент начала движения и в момент падения на землю. Начальная и конечная скорости движения тела равны:
vmax = vo = v
Время подъема — время, которое требуется телу, чтобы достигнуть верхней точки траектории. В этой точке проекция скорости на ось ОУ равна нулю: vy = 0. Время подъема определяется следующей формулой:
Полное время — это время всего полета тела от момента бросания до момента приземления. Так как время падения равно времени подъема, формула для определения полного времени полета принимает вид:
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0x tполн = v0 cosα tполн
Подставляя в выражение формулу полного времени полета, получаем:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости на эту ось равна v0 cosα, данная формула принимает вид:
x = v0 cosα t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Учитывая, что начальная координата равна 0, проекция начальной скорости на ось ОУ равна v0 sinα, а проекция ускорения свободного падения на эту ось равна –g, эта формула принимает вид:
Наибольшая высота подъема — расстояние от земли до верхней точки траектории. Наибольшая высота подъема обозначается h и вычисляется по формуле:
Пример №1. Небольшой камень бросили с ровной горизонтальной поверхности под углом к горизонту. На какую максимальную высоту поднялся камень, если ровно через 1 с после броска его скорость была направлена горизонтально?
Скорость направляется горизонтально в верхней точке полета. Значит, время подъема равно 1 с. Из формулы времени подъема выразим произведение начальной скорости на синус угла, под которым было брошено тело:
v0 sinα = gtпод
Подставим полученное выражение в формулу для определения наибольшей высоты подъема и сделаем вычисления:
Тело, брошенное под углом к горизонту с некоторой высоты
Когда тело бросают под углом к горизонту с некоторой высоты, характер его движения остается прежним. Но приземлится оно дальше по сравнению со случаем, если бы тело бросали с ровной поверхности.
Важные факты!
График движения тела, брошенного под углом к горизонту с некоторой высоты:
Время падения тела больше времени его подъема: tпад > tпод.
Полное время полета равно:
tполн = tпад + tпод
Уравнение координаты x:
x = v0 cosα t
Уравнение координаты y:
Пример №2. С балкона бросили мяч под углом 60 градусов к горизонту, придав ему начальную скорость 2 м/с. До приземления мяч летел 3 с. Определить дальность полета мяча.
Косинус 60 градусов равен 0,5. Подставляем известные данные в формулу:
x = v0 cosα t = 2 ∙ 0,5 ∙ 3 = 3 м.
Задание EF17562
С высоты Н над землёй начинает свободно падать стальной шарик, который через время t = 0,4 c сталкивается с плитой, наклонённой под углом 30° к горизонту. После абсолютно упругого удара он движется по траектории, верхняя точка которой находится на высоте h = 1,4 м над землёй. Чему равна высота H? Сделайте схематический рисунок, поясняющий решение.
Алгоритм решения
1.Записать исходные данные.
2.Построить на чертеже начальное и конечное положения тела. Выбрать систему координат.
3.Выбрать нулевой уровень для определения потенциальной энергии.
4.Записать закон сохранения энергии.
5.Решить задачу в общем виде.
6.Подставить числовые значения и произвести вычисления.
Решение
Запишем исходные данные:
• Время падения стального шарика: t = 0,4 c.
• Верхняя точка траектории после абсолютно упругого удара о плиту: h = 1,4 м.
• Угол наклона плиты: α = 30о.
Построим чертеж и укажем на нем все необходимое:
Нулевой уровень — точка D.
Закон сохранения энергии:
Ek0 + Ep0 = Ek + Ep
Потенциальная энергия шарика в точке А равна:
EpA = mgH
Кинетическая энергия шарика в точке А равна нулю, так как скорость в начале свободного падения нулевая.
В момент перед упругим ударом с плитой в точке В потенциальная энергия шарика минимальна. Она равна:
EpB=mgl1
Перед ударом кинетическая энергия шарика равна:
EkB=mv22
Согласно закону сохранения энергии:
EpA=EpB+EkB
mgH=mgl1+mv22
Отсюда высота H равна:
H=mgl1mg+mv22mg=l1+v22g
Относительно точки В шарик поднимется на высоту h – l1. Но данный участок движения можно рассматривать как движение тела, брошенного под углом к горизонту. В таком случае высота полета определяется формулой:
h−l1=v2sin2β2g=v2sin2(90−2α)o2g
Отсюда:
l1=h−v2sin2(90−2α)o2g
Шарик падал в течение времени t, поэтому мы можем рассчитать высоту шарика над плитой и его скорость в точке В:
v=gt
Следовательно:
H=l1+v22g=h−(gt)2sin2(90−2α)o2g+(gt)22g
H=h−gt2sin2(90−2α)2+gt22=h−gt22(sin2(90−2α)o−1)
H=1,4−10·0,422(sin2(90−60)o−1)
H=1,4−5·0,16(sin230o−1)
H=1,4−0,8((12)2−1)=1,4−0,8(14−1)
H=1,4+0,6=2 (м)
Ответ: 20
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17980
В момент t=0 мячик бросают с начальной скоростью v0 под углом α к горизонту с балкона высотой h (см. рисунок).
Графики А и Б представляют собой зависимости физических величин, характеризующих движение мячика в процессе полёта, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. (Сопротивлением воздуха пренебречь. Потенциальная энергия мячика отсчитывается от уровня y=0).
К каждой позиции графика подберите соответствующую позицию утверждения и запишите выбранные цифры в порядке АБ.
Алгоритм решения
- Установить вид механического движения, исходя из условий задачи.
- Записать формулы для физических величин, указанных в таблице, в соответствии с установленным видом механического движения.
- Определить, как зависят эти величины от времени.
- Установить соответствие между графиками и величинами.
Решение
Исходя из условия задачи, мячик движется неравномерно. Этот случай соответствует движению тела, брошенного под углом к горизонту.
Записываем формулы для физических величин из таблицы, учитывая, что речь идет о движении тела, брошенного под углом к горизонту.
Координата x меняется согласно уравнению координаты x:
Так как начальная координата нулевая, а проекция ускорения свободного падения тоже равна нулю, это уравнение принимает вид:
Проекция скорости мячика на ось ОХ равна произведению начальной скорости на время и косинус угла, под которым мячик был брошен. Поэтому уравнение координаты x принимает вид:
В этом уравнении начальная скорость и угол α — постоянные величины. Меняется только время. И оно может только расти. Поэтому и координата x может только расти. В этом случае ей может соответствовать график, представляющий собой прямую линии, не параллельную оси времени. Но графики А и Б не могут описывать изменение этой координаты.
Формула проекции скорости мячика на ось ОХ:
Начальная скорость и угол α — постоянные величины. И больше ни от чего проекция скорости на ось ОХ не зависит. Поэтому ее может охарактеризовать график в виде прямой линии, параллельной оси времени. Такой график у нас есть — это Б.
Кинетическая энергия мячика равна половине произведения массы мячика на квадрат его мгновенной скорости. По мере приближения к верхней точке полета скорость тела уменьшается, а затем растет. Поэтому кинетическая энергия также сначала уменьшается, а затем растет. Но на графике А величина наоборот — сначала увеличивается, потом уменьшается. Поэтому он не может быть графиком зависимости кинетической энергии мячика от времени.
Остается последний вариант — координата y. Уравнение этой координаты имеет вид:
Это квадратическая зависимость, поэтому графиком зависимости координаты y от времени может быть только парабола. Так как мячик сначала движется вверх, а потом — вниз, то и график должен сначала расти, а затем — убывать. График А полностью соответствует этому описанию.
Теперь записываем установленные соответствия в порядке АБ: 42.
Ответ: 42
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18741
Мальчик бросил стальной шарик вверх под углом к горизонту. Пренебрегая сопротивлением воздуха, определите, как меняются по мере приближения к Земле модуль ускорения шарика и горизонтальная составляющая его скорости?
Для каждой величины определите соответствующий характер изменения:
- увеличивается
- уменьшается
- не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулы, определяющие указанные в условии задачи величины.
- Определить характер изменения физических величин, опираясь на сделанный чертеж и формулы.
Решение
Выполняем чертеж:
Модуль ускорения шарика |g| — величина постоянная, так как ускорение свободного падения не меняет ни направления, ни модуля. Поэтому модуль ускорения не меняется (выбор «3»).
Горизонтальная составляющая скорости шарика определяется формулой:
vx = v0 cosα
Угол, под которым было брошено тело, поменяться не может. Начальная скорость броска тоже. Больше ни от каких величин горизонтальная составляющая скорости не зависит. Поэтому проекция скорости на ось ОХ тоже не меняется (выбор «3»).
Ответом будет следующая последовательность цифр — 33.
Ответ: 33
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 43.3k
|
0 / 0 / 0 Регистрация: 08.07.2017 Сообщений: 11 |
|
|
1 |
|
Расчета угла отскока шарика от стены30.07.2017, 18:08. Показов 24853. Ответов 4
Нужно реализовать метод для расчета угла отскока шарика от стены. Считайте, что угол падения равен углу отражения, то есть можно пренебречь всеми физическими эффектами, связанными с кручением шаров, трением шара об стенку и т.п.
0 |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
30.07.2017, 18:08 |
|
Ответы с готовыми решениями:
Определить угол отскока шарика от преграды Вычисление угла отскока теннисного мяча Формула для расчёта угасания (затухания или ослабления) радиосигнала через стены, двери, окна. 4 |
|
201 / 119 / 85 Регистрация: 15.12.2016 Сообщений: 235 |
|
|
30.07.2017, 21:02 |
2 |
|
Если пренебрегая всякими физическими эффектами, то формула простая:
1 |
|
201 / 119 / 85 Регистрация: 15.12.2016 Сообщений: 235 |
|
|
30.07.2017, 21:07 |
3 |
|
Недеюсь, это то, что нужно Миниатюры
1 |
|
0 / 0 / 0 Регистрация: 08.07.2017 Сообщений: 11 |
|
|
30.07.2017, 23:10 [ТС] |
4 |
|
похоже на правду, спасибо
0 |
|
novac_33 2 / 2 / 0 Регистрация: 26.04.2016 Сообщений: 42 |
||||
|
06.04.2018, 11:23 |
5 |
|||
|
Вдруг кому понадобится
2 |






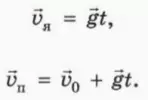
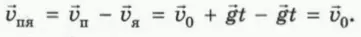
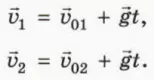
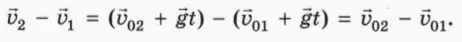
















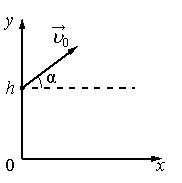








 Интересует расчет угла отскока шарика от горизонтальных, вертикальных и произвольных стен
Интересует расчет угла отскока шарика от горизонтальных, вертикальных и произвольных стен