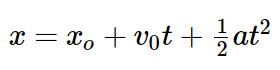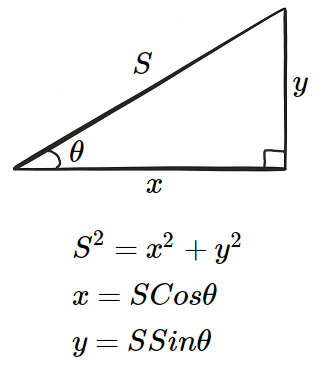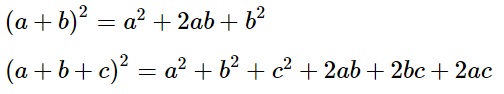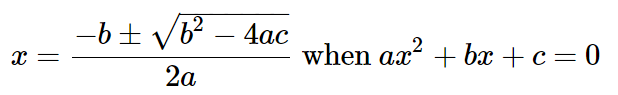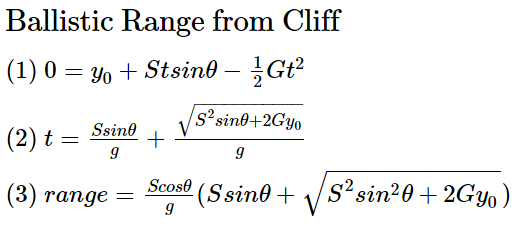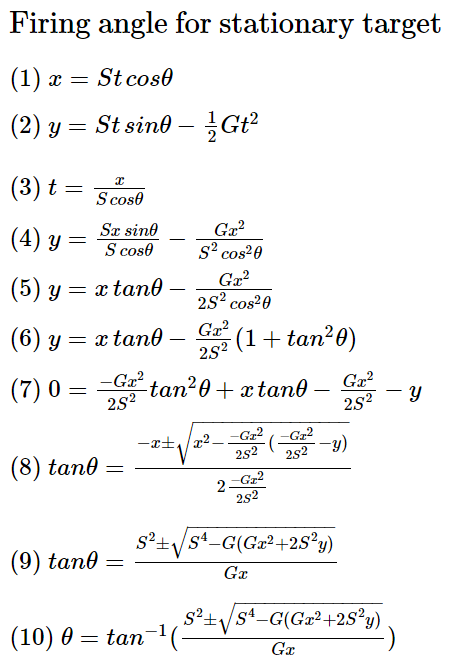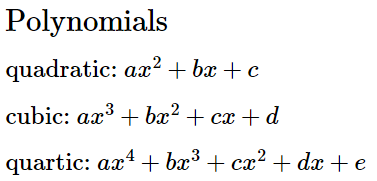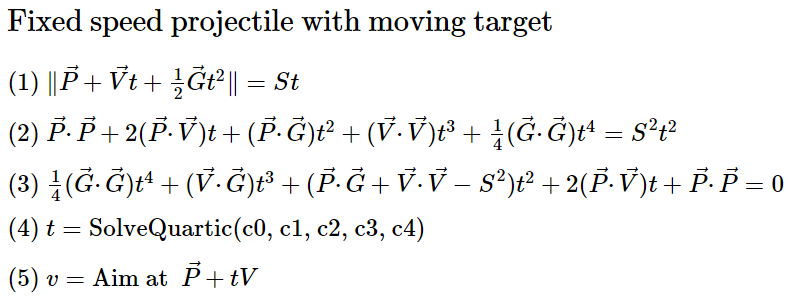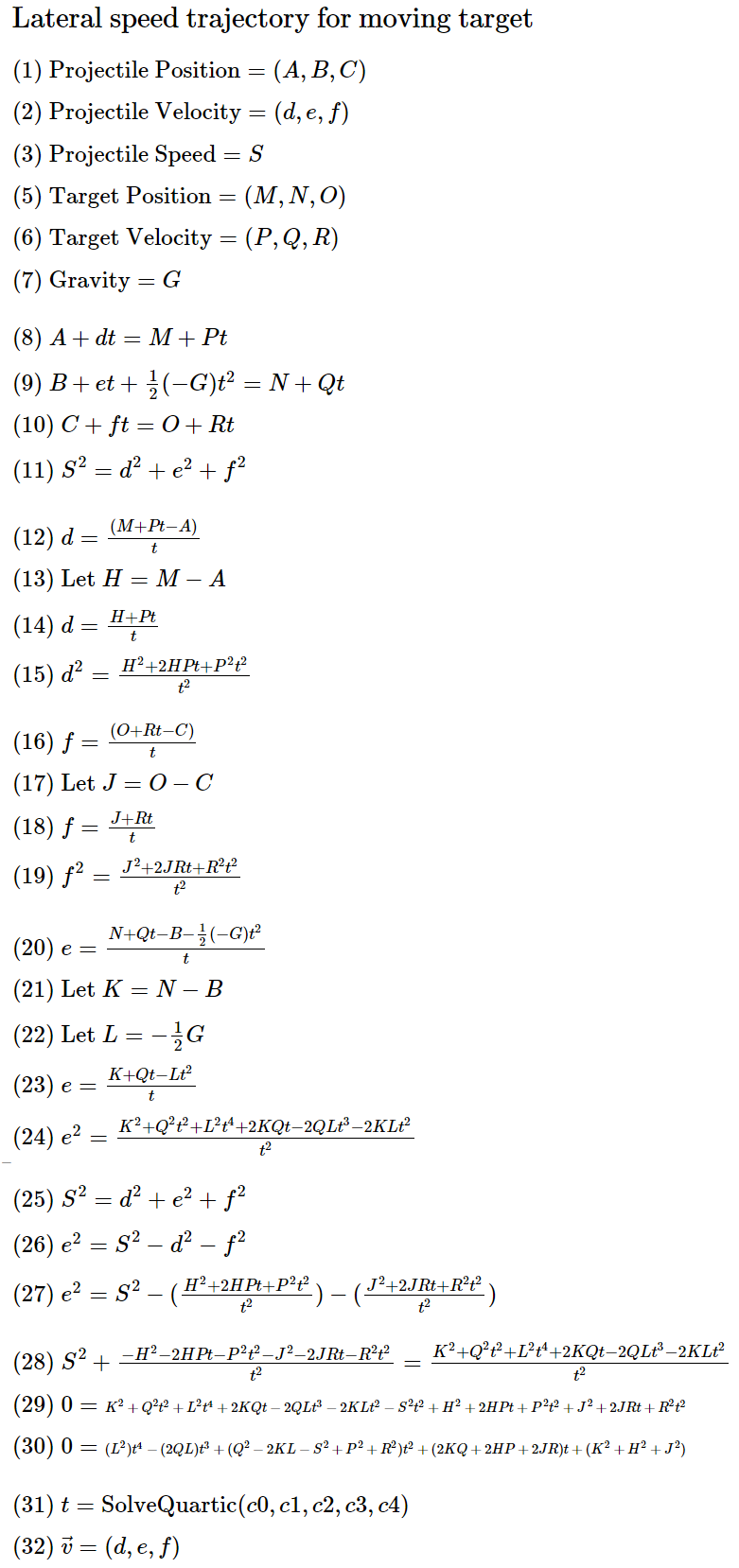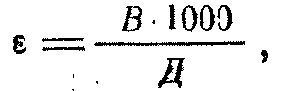Когда объект запускается, он следует параболическому пути и движению, известному как движение снаряда. В этом посте мы рассмотрим параметры и способы их расчета. движение снаряда в подробном анализе.
Когда объект запускается и движется по симметричной параболической траектории, движение называется движением снаряда, а параболический путь объекта называется его траекторией. В этом случае объект перемещается одновременно по вертикали и горизонтали. В результате движение снаряда становится двумерным. При движении снаряда вам нужно только приложить силу в начале траектории; после этого на объект действует только сила тяжести.
Теперь давайте посмотрим, как рассчитать движение снаряда:
Предположим, вы стреляете пушечным ядром. Он начинает двигаться вверх и вперед, пока не достигнет максимальной высоты. С этого момента он будет продолжать двигаться вперед, но в нисходящем направлении. Он отслеживает этот изогнутый маршрут, известный как траектория, имеющая форму параболы. Любой объект, движущийся таким образом, называется движущимся снарядом. Поскольку траектория движения снаряда всегда параболическая, она представляется как:
у = ах + bx2
Прежде чем достичь Земли, пушечное ядро во время своего путешествия пойдет по параболическому маршруту. Компания скорость по оси X остается постоянной на протяжении всего движения, тогда как скорость по оси Y изменяется в зависимости от его положения. Только ускорение свободного падения 9.8 м / с2, управляет этим типом движения. Ускорение, направленное вниз, остается постоянным во время полета ядер.
Кинематические уравнения движения снаряда:
Формула начальной скорости:
Предположим, что начальная скорость равна u, а угол полета снаряда равен. У начальной скорости есть две составляющие: горизонтальная и вертикальная.
Горизонтальная составляющая начальной скорости ux и предоставлено:
ux = ты ᐧ потому что𝛳
Вертикальная составляющая начальной скорости равна uy и определяется выражением:
uy = и ᐧ грех

Время полета снаряда:
Время полета снаряда — это промежуток времени между запускаемым объектом и достижением земли. Величина стартовой скорости и угол полета снаряда определяют время полета, которое обозначается T.
Формула ускорения:
В горизонтальном направлении ускорение отсутствует, поскольку горизонтальная составляющая ускорения остается постоянной на протяжении всего движения. Единственное ускорение в вертикальном направлении происходит за счет силы тяжести.
ax = 0 и
ay = -г
Отрицательный знак означает ускорение вниз.
Формула скорости в момент времени t:
На протяжении всего движения горизонтальная составляющая скорости остается постоянной. Однако, поскольку вертикальное ускорение постоянно, вертикальная составляющая скорости изменяется линейно.
В результате скорость может быть рассчитана в любой момент времени t по следующей формуле:
vx = тыx = ты ᐧ потому что𝛳
vy = u ᐧ sin𝛳 — g ᐧ t
Используя теорему Пифагора, можно найти величину скорости.
Формула смещения в момент времени t:
В момент времени t смещение может быть определено как:
х = (и ᐧ cos𝛳) ᐧ т
y = (u ᐧ sin𝛳) ᐧ t — ½ (gt2)
Формула параболической траектории:
Мы можем использовать уравнения смещения в направлениях x и y, чтобы вывести уравнение для параболической формы движения снаряда:
Формула дальности снаряда:
Общее горизонтальное расстояние, пройденное объектом за время полета, определяется как его дальность. Если объект запускается с земли (начальная высота = 0), формула выглядит следующим образом:
Согласно приведенному выше уравнению, максимальная дальность полета по горизонтали может быть получена при угле полета снаряда 𝛳 = 45 °. Rm представляет собой максимальный диапазон.
Формула максимальной высоты:
Когда вертикаль составляющая скорости равна нулю, vy = 0, максимальная высота может быть достигнута. Поскольку время полета — это полное время снаряда, для достижения максимальной высоты потребуется половина этого времени. Таким образом, время для достижения максимальной высоты составляет:
Таким образом, из уравнения перемещения максимальная высота может быть определена как:
Формула движения снаряда по горизонтали:
Горизонтальный снаряд Движение — это тип движения снаряда, при котором объект запускается горизонтально с возвышенной плоскости, а не с земли.

Угол запуска указывать не нужно, поскольку он параллелен земле (т. Е. Угол равен 0 °). В результате у нас есть только одна начальная составляющая скорости: Vx = V, тогда как Vy = 0.
В этом случае уравнения движения следующие:
Скорость горизонтального движения снаряда:
Горизонтальная скорость: vx = V
И вертикальная скорость: vx = -g ᐧ т
Расстояние, пройденное объектом при горизонтальном движении снаряда:
В этом случае горизонтальное расстояние рассчитывается следующим образом:
х = v ᐧ т
А расстояние по вертикали можно определить как:
y = — (g ᐧ t2) / 2
Ускорение при горизонтальном движении снаряда:
Горизонтальное ускорение ax = 0, так как горизонтальная скорость постоянна..
Вертикальное ускорение аy = -г
Уравнение траектории горизонтального движения снаряда:
Уравнение траектории в этом случае может быть задано следующим образом:
Время полета при горизонтальном движении снаряда:
Время полета в этом случае может быть определено как:
Дальность полета снаряда при горизонтальном движении снаряда:
Дальность полета снаряда при горизонтальном движении снаряда составляет:
Поскольку мы запускаем объект с максимальной высоты, нам не нужно рассчитывать максимальную высоту в этом сценарии.
Давайте посмотрим на некоторые проблемы движения снаряда.
Проблема 1: Каким будет θmax, при котором расстояние от частицы до метателя всегда увеличивается до конца пути снова у земли?
Решение: Горизонтальное расстояние, пройденное объектом, называется его горизонтальным диапазоном и определяется по формуле:
Максимальная дальность полета может быть достигнута при угле выстрела 45 °.
Таким образом, для максимального угла Rm θmax = 45 °.
Задача 2: Если мяч брошен вертикально вверх со скоростью u, расстояние, пройденное за последние t секунд его всплытия, будет:
Решение: Поскольку мяч брошен вертикально, угол полета снаряда 𝛳 = 90 °.
Поскольку 𝛳 = 90 °
Где Tm — время, необходимое объекту для достижения максимальной высоты.
Предположим, что h представляет собой расстояние, пройденное объектом за последние t секунд его подъема. Затем скорость в этот момент рассчитывается следующим образом:
V = u — g ᐧ (T — t)
= u — g ᐧ (u / g — t)
= гт
Таким образом, расстояние, пройденное за последнюю t секунду, составляет:
h = vt — ½ gt2
= гт2 — ½ гт2
= ½ гт2
3 задачи: Частица проецируется под углом 60 ° над горизонтом со скоростью 10 м / с. Через некоторое время скорость составит угол 30 ° от горизонтали. Скорость частицы в этот момент составляет?
Решение: Горизонтальная составляющая скорости определяется как:
vx = ты ᐧ потому что𝛳
Здесь в первом случае угол проекции составляет 60 °, а начальная скорость u = 10 м / с. Таким образом,
vx = ты ᐧ cos60
= 10 x 0.5
= 5 м / с.
Теперь вертикальная составляющая скорости vy изменяется во время движения, но vx остается постоянным. Таким образом,
vx = v ᐧ cos𝛳2
Где 𝛳2 = 30 °, а v — скорость, когда объект составляет угол 𝛳 = 30 ° с горизонтом.
Вычисляем баллистические траектории в играх
Время на прочтение
7 мин
Количество просмотров 23K
При разработке видеоигр часто встречается задача вычисления угла выстрела для попадания в цель. Она настолько распространена, что я писал код для её решения в буквальном смысле для каждой игры, над которой работал.
Когда возникала эта проблема, я обычно брал ручку с блокнотом и решал её с нуля. Мне это надоело. Чтобы сэкономить себе из будущего немного времени, я выложу это решение в Интернет. Кроме того, я расскажу о необычной «фишке», которую предпочитаю использовать из соображений эстетики.
Уравнения движения
Задача всегда начинается одинаково. У нас есть стреляющий и цель: под каким углом нужно стрелять снарядом, чтобы он поразил цель?
Существует четыре основных уравнения движения. В статье мы воспользуемся только одним.
Если объяснять на словах, то конечная позиция РАВНА исходной позиции ПЛЮС скорость, умноженная на время ПЛЮС половина ускорения, умноженная на время в квадрате. Это простое уравнение, для его решения необходимо немного алгебры и несколько тригонометрических тождеств.
Освежим знания
Прежде чем начать, давайте вкратце освежим память.
Если дан снаряд с постоянной скоростью S и углом выстрела θ (theta), то мы можем вычислить компоненты скорости x и y. Или если есть S и мы каким-то образом найдём y, то можем вычислить θ и x.
Мы используем алгебру.
Мы часто будем пользоваться формулой корней квадратного уравнения.
Дальность
При разработке видеоигр нам, вероятно, нужно будет знать максимальную дальность полёта снаряда. Искусственный интеллект должен понимать, насколько близко нужно подойти, а игрокам нужны чёткие наглядные индикаторы опасных зон.
Существует очень простое уравнение максимальной дальности на плоской поверхности. Мы сразу же ринемся в омут с головой и начнём с обобщённого вида.
Если дан снаряд с постоянной скоростью (S) и гравитацией (G), то какой будет его максимальная дальность полёта?
- Подставим известные нам переменные (y0, S, G) в основное уравнение движения.
- Применим формулу корней квадратного уравнения. Отбросим меньшее значение.
- Подставим t в x = S*cos θ*t и упростим.
Демо
Для тестирования и визуализации я создал демо на Unity. В нём используются чайники, стреляющие чайниками. Пиф-паф!
Демо: Unity-демо в WebGL
В демо есть несколько ползунков. В видео показан индикатор дальности стрельбы нашего чайника-турели. При увеличении скорости увеличивается дальность. При снижении гравитации дальность тоже растёт. Всё довольно просто.
Угол стрельбы для попадания по неподвижной мишени
Теперь начинается интересное.
Если снаряд имеет постоянную скорость (S), а гравитация равна (G), то под каким углом его нужно выстреливать, чтобы попасть в неподвижную мишень?
Бах. Теперь у нас есть два уравнения и два неизвестных. Давайте их проанализируем.
- Первое уравнение, два неизвестных (t, θ)
- Второе уравнение, два неизвестных (t, θ)
- Вычислить t из (1)
- Подставить (3) в (2)
- Тригонометрическая подстановка: sin θ/cosθ = tanθ
- Тригонометрическая подстановка: 1/(cos θ)^2 = 1 + (tan θ)^2
- Развернём и преобразуем
- Формула корней квадратного уравнения
- Умножим верхнюю/нижнюю часть на -S^2/x. Перенесём S^4/x^2 под корень
- Применим к каждой части арктангенс
Та-да! В результате мы получили два угла. Один высокий и один низкий. Вот как это выглядит на практике.
Визуальное несовершенство
Взгляните на показанный выше gif. Когда чайник начинает стрелять, всё выглядит довольно неплохо. Высокая дуга красива и радует глаз. Низкая дуга кажется чёткой и эффективной.
Однако при увеличении дальности всё становится не таким красивым. Низкая дуга почти плоская. Высокая дуга чрезмерно высока. В этом и заключается проблема снаряда с постоянной скоростью. Он выглядит красиво, только когда цель находится на границах его радиуса дальности.
Существует ли способ получше?
Скорость горизонтального перемещения
Я часто предпочитаю задавать горизонтальную скорость снаряда, только в плоскости земли. Тогда я могу явным образом задать высоту дуги. То есть переменной становится скорость и гравитация.
Такой подход имеет множество преимуществ. Во-первых, он всегда выглядит красиво!
Во-вторых, его дизайн более интуитивен. Дизайнеров не волнует абсолютная скорость. Им важно, что турель имеет дальность 20 метров и что для перемещения на это расстояние снарядам требуется 1 секунда. Они не обязаны пользоваться строящим графики калькулятором, чтобы менять значения баланса. А художественные изменения не должны влиять на геймплейные механики.
В-третьих, так проще попадать по движущейся мишени. Чуть позже я раскрою это подробнее.
Вот как это выглядит:
Вычисление скорости горизонтального перемещения
Если дан снаряд с горизонтальной скоростью (S) и пиковой высотой (y_peak), то какими должны быть скорость и гравитация для поражения неподвижной мишени?
- Основное уравнение движения
- Решаем (1), подставив 2
- Зададим, что y_peak (пользовательская константа) снаряд достигает во время (1/2)t
- Зададим, что y_end (высота цели) снаряд достигает во время t
- Магия!
- Ещё магия!
- Вектор стрельбы равен (S, v.y) с гравитационным ускорением g
Вуаля! Хотя постойте-ка. Магия? Это жульничество! Да, но вполне оправданное.
Пункты (3) и (4) — это ещё два уравнения с двумя неизвестными. Я ленивый и не хочу их записывать. Плюс я запутаюсь и перепутаю знак, поэтому позволю компьютеру решить их за меня.
Точнее, я воспользовался Wolfram Alpha. Рекомендую каждому иметь Wolfram в своём инструментарии, он довольно полезен.
Если a+c == 2b, то y0, y_peak и y_end лежат на одной прямой. То есть мы стреляем по прямой.
Скорость горизонтального перемещения при подвижной мишени
Итак, у нас есть два разных вычисления траектории. Однако враги обычно не стоят на месте, они перемещаются. Нам нужно вычислять траекторию, чтобы поражать подвижную мишень.
Именно здесь проявляются все достоинства скорости горизонтального перемещения. Задав скорость в плоскости земли, очень просто выполнить вычисления для подвижной мишени.
- Где X — позиция мишени, а V — её скорость
- Возводим обе части в квадрат.
- Преобразуем в квадратное уравнение
- Применяем формулу корней квадратного уравнения
Пункты с 5 по 9 см. в предыдущем разделе.
Меня это очень радует. Пиу-пиу-пиу!
Постоянная скорость с подвижной мишенью
А что если нам нужно поразить подвижную мишень снарядом с постоянной скоростью? Ой-ёй. Это очень запутанная задача! Даже не знаю, как к ней подступиться.
За всю мою карьеру мне не доводилось её решать. Обычно в играх не нужна точная артиллерия. Это просто неинтересно! Вместо этого мы приблизительно вычисляем будущую позицию и целимся в случайную точку рядом с ней. Игроки воспринимают артиллерийский огонь как дождь из глупых снарядов, а не как гарантированную смерть с лазерным наведением.
В процессе написания этого поста я нашёл решение задачи снаряда с постоянной скоростью и движущейся мишени, которого не было в Интернете в готовом виде. Стоит заметить, что вам, вероятно, не понадобится реализовывать его в своей игре. Но я потратил на него много времени, поэтому не хочу, чтобы оно было потеряно впустую!
Уравнения четвёртой степени
Скорее всего, вы не захотите использовать его в своей игре именно из-за уравнений четвёртой степени. По сути, для решения требуется одно из таких уравнений.
Квадратные уравнения имеют простое и изящное решение в виде формулы корней квадратного уравнения. Кубические уравнения решаемы несколькими разными способами. Однако уравнения четвёртой степени — это настоящая головная боль.
Решение таких уравнений находится далеко за рамками этой статьи. Честно говоря, и за пределами моих математических способностей. К счастью для нас, в книге 1990 года Graphics Gems I есть код для решения уравнений четвёртого порядка. Я использовал этот код для своего демо. Не могу гарантировать его точности и численной устойчивости, используйте его крайне осмотрительно.
Способ первый
Итак, давайте его решим. Каким должен быть угол выстрела снарядом с постоянной скоростью по движущейся мишени? Этот способ взят из поста 2007 года Джеймса Макнейлла и дополнен информацией Райана Джакетта.
- Где P — позиция мишени, а V — скорость мишени
- Возводим обе части в квадрат
- Преобразуем
- Вычисляем коэффициенты уравнения четвёртого порядка и вставляем в SolveQuartic
- Используем t для вычисления позиции мишени при вычислении траектории до неподвижной точки.
Способ работает. Все сложные задачи выполняет SolveQuartic. Затем мы используем решение для неподвижной мишени, изложенное выше.
Способ второй
Прежде чем я нашёл первый способ, я вывел решение другим способом. Оно состоит из гораздо большего количества шагов. Однако я нахожу конечный результат более изящным. Плюс я потратил примерно восемь листов бумаги и не хочу, чтобы эти деревья пожертвовали собой зазря.
Чёрт возьми. 32 шага!? Это хуже, чем кажется.
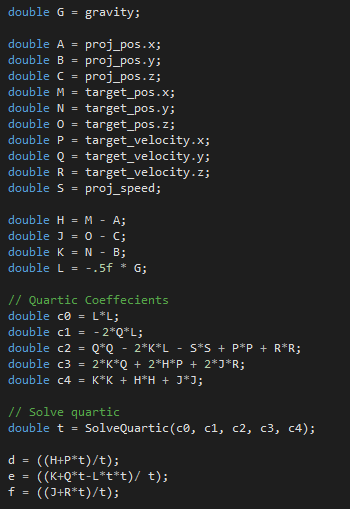
1–7 — объявляем переменные.
8–11 — объявляем систему уравнений. Четыре уравнения, четыре неизвестных — d, e, f, t.
12–15 — вычисляем по (8) величину d. Перемножаем d^2 на будущее.
16–19 — вычисляем по (10) величину f. Перемножаем f^2 на будущее.
20–24 — вычисляем по (9) величину e. Перемножаем e^2 на будущее.
25–27 — вычисляем по (11) величину e^2. Подставляем d^2 и f^2.
28–30 — приравниваем (27) к (24). Умножаем на t^2 и преобразуем в уравнение четвёртой степени.
31 — подставляем коэффициенты в SolveQuartic.
32 — подставляем положительные вещественные корни в (14), (18), (23) для d, e, f.
Код довольно короткий. Объявлению переменных отведено больше строк, чем самим вычислениям! Разумеется, кроме SolveQuartic.
Предупреждение
Код, написанный для этого теста, не проверен в бою, а пост никем не рецензировался. Вероятно, в нём есть несколько опечаток, ошибок и неучтённых пограничных случаев. Если найдёте подобные ошибки, пожалуйста, сообщите мне. Втайне, чтобы никто не узнал о моём позоре.
Рассматривайте этот код не как готовое решение, а как опорную точку.
Инструменты
При создании этого поста я использовал несколько инструментов. Многие из них были для меня новыми.
- Unity для создания демо.
- Paper, Affinity Designer и MSPaint для создания изображений.
- Arachnid Latex + MathJax для формул LaTeX.
- FFmpeg для преобразования последовательности скриншотов в анимацию.
- Gfycat для встраивания анимаций.
- Чайник из Юты. Пиу-пиу!
Синтаксис LaTeX ужасен, его сложно учить. Все формулы LaTeX можно найти здесь. Вот пример:
Заключение
Вот и всё. Я потратил на этот пост гораздо больше времени, чем ожидал. Я решил задачу, которую никогда не решал прежде и изучил несколько новых инструментов. И это того стоило.
В этом посте нет ничего нового или оригинального. Я пытался объяснять подробно, но чтобы не быть при этом слишком многословным. Мне очень нравится, что теперь полные описания можно найти в одном месте. Надеюсь, они окажутся полезными для людей.
Исходный код
Проект Unity
Unity-демо в WebGL
Parabolic water motion trajectory
Components of initial velocity of parabolic throwing
Ballistic trajectories are parabolic if gravity is homogeneous and elliptic if it is round.
Projectile motion is a form of motion experienced by an object or particle (a projectile) that is projected in a gravitational field, such as from Earth’s surface, and moves along a curved path under the action of gravity only. In the particular case of projectile motion on Earth, most calculations assume the effects of air resistance are passive and negligible. The curved path of objects in projectile motion was shown by Galileo to be a parabola, but may also be a straight line in the special case when it is thrown directly upward or downward. The study of such motions is called ballistics, and such a trajectory is a ballistic trajectory. The only force of mathematical significance that is actively exerted on the object is gravity, which acts downward, thus imparting to the object a downward acceleration towards the Earth’s center of mass. Because of the object’s inertia, no external force is needed to maintain the horizontal velocity component of the object’s motion. Taking other forces into account, such as aerodynamic drag or internal propulsion (such as in a rocket), requires additional analysis. A ballistic missile is a missile only guided during the relatively brief initial powered phase of flight, and whose remaining course is governed by the laws of classical mechanics.
Ballistics (from Ancient Greek βάλλειν bállein ‘to throw’) is the science of dynamics that deals with the flight, behavior and effects of projectiles, especially bullets, unguided bombs, rockets, or the like; the science or art of designing and accelerating projectiles so as to achieve a desired performance.
Trajectories of a projectile with air drag and varying initial velocities
The elementary equation of ballistics neglect nearly every factor except for initial velocity and an assumed constant gravitational acceleration. Practical solutions of a ballistics problem often require considerations of air resistance, cross winds, target motion, varying acceleration due to gravity, and in such problems as launching a rocket from one point on the Earth to another, the rotation of the Earth. Detailed mathematical solutions of practical problems typically do not have closed-form solutions, and therefore require numerical methods to address.
Kinematic quantities[edit]
In projectile motion, the horizontal motion and the vertical motion are independent of each other; that is, neither motion affects the other. This is the principle of compound motion established by Galileo in 1638,[1] and used by him to prove the parabolic form of projectile motion.[2]
The horizontal and vertical components of a projectile’s velocity are independent of each other.
A ballistic trajectory is a parabola with homogeneous acceleration, such as in a space ship with constant acceleration in absence of other forces. On Earth the acceleration changes magnitude with altitude and direction with latitude/longitude. This causes an elliptic trajectory, which is very close to a parabola on a small scale. However, if an object was thrown and the Earth was suddenly replaced with a black hole of equal mass, it would become obvious that the ballistic trajectory is part of an elliptic orbit around that black hole, and not a parabola that extends to infinity. At higher speeds the trajectory can also be circular, parabolic or hyperbolic (unless distorted by other objects like the Moon or the Sun). In this article a homogeneous acceleration is assumed.
Acceleration[edit]
Since there is acceleration only in the vertical direction, the velocity in the horizontal direction is constant, being equal to 
,
.
Velocity[edit]
Let the projectile be launched with an initial velocity 
.
The components 


,
The horizontal component of the velocity of the object remains unchanged throughout the motion. The vertical component of the velocity changes linearly,[note 2] because the acceleration due to gravity is constant. The accelerations in the x and y directions can be integrated to solve for the components of velocity at any time t, as follows:
,
.
The magnitude of the velocity (under the Pythagorean theorem, also known as the triangle law):
.
Displacement[edit]
Displacement and coordinates of parabolic throwing
At any time 
,
.
The magnitude of the displacement is:
.
Consider the equations,
.
If t is eliminated between these two equations the following equation is obtained:
Here R is the Range of a projectile.
Since g, θ, and v0 are constants, the above equation is of the form
,
in which a and b are constants. This is the equation of a parabola, so the path is parabolic. The axis of the parabola is vertical.
If the projectile’s position (x,y) and launch angle (θ or α) are known, the initial velocity can be found solving for v0 in the aforementioned parabolic equation:
.
Displacement in polar coordinates[edit]
The parabolic trajectory of a projectile can also be expressed in polar coordinates instead of Cartesian coordinates. In this case, the position has the general formula
.
In this equation, the origin is the midpoint of the horizontal range of the projectile, and if the ground is flat, the parabolic arc is plotted in the range 


Properties of the trajectory[edit]
Time of flight or total time of the whole journey[edit]
The total time t for which the projectile remains in the air is called the time of flight.
After the flight, the projectile returns to the horizontal axis (x-axis), so 
Note that we have neglected air resistance on the projectile.
If the starting point is at height y0 with respect to the point of impact, the time of flight is:
As above, this expression can be reduced to
if θ is 45° and y0 is 0.
Time of flight to the target’s position[edit]
As shown above in the Displacement section, the horizontal and vertical velocity of a projectile are independent of each other.
Because of this, we can find the time to reach a target using the displacement formula for the horizontal velocity:



This equation will give the total time t the projectile must travel for to reach the target’s horizontal displacement, neglecting air resistance.
Maximum height of projectile[edit]
Maximum height of projectile
The greatest height that the object will reach is known as the peak of the object’s motion.
The increase in height will last until 
.
Time to reach the maximum height(h):
.
For the vertical displacement of the maximum height of projectile:
The maximum reachable height is obtained for θ=90°:
If the projectile’s position (x,y) and launch angle (θ) are known, the maximum height can be found solving for h in the following equation:
Relation between horizontal range and maximum height[edit]
The relation between the range d on the horizontal plane and the maximum height h reached at 
Maximum distance of projectile[edit]
The maximum distance of projectile
The range and the maximum height of the projectile does not depend upon its mass. Hence range and maximum height are equal for all bodies that are thrown with the same velocity and direction.
The horizontal range d of the projectile is the horizontal distance it has traveled when it returns to its initial height (
.
Time to reach ground:
.
From the horizontal displacement the maximum distance of projectile:
,
so[note 3]
.
Note that d has its maximum value when
,
which necessarily corresponds to
,
or
.
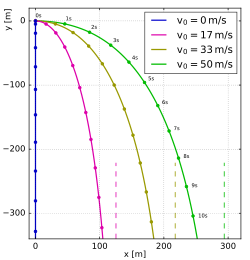
Trajectories of projectiles launched at different elevation angles but the same speed of 10 m/s in a vacuum and uniform downward gravity field of 10 m/s2. Points are at 0.05 s intervals and length of their tails is linearly proportional to their speed. t = time from launch, T = time of flight, R = range and H = highest point of trajectory (indicated with arrows).
The total horizontal distance (d) traveled.
When the surface is flat (initial height of the object is zero), the distance traveled:[3]
Thus the maximum distance is obtained if θ is 45 degrees. This distance is:
Application of the work energy theorem[edit]
According to the work-energy theorem the vertical component of velocity is:
.
These formulae ignore aerodynamic drag and also assume that the landing area is at uniform height 0.
Angle of reach[edit]
The «angle of reach» is the angle (θ) at which a projectile must be launched in order to go a distance d, given the initial velocity v.
There are two solutions:
(shallow trajectory)
and
(steep trajectory)
Angle θ required to hit coordinate (x, y)[edit]
Vacuum trajectory of a projectile for different launch angles. Launch speed is the same for all angles, 50 m/s if «g» is 10 m/s2.
To hit a target at range x and altitude y when fired from (0,0) and with initial speed v the required angle(s) of launch θ are:
The two roots of the equation correspond to the two possible launch angles, so long as they aren’t imaginary, in which case the initial speed is not great enough to reach the point (x,y) selected. This formula allows one to find the angle of launch needed without the restriction of 
One can also ask what launch angle allows the lowest possible launch velocity. This occurs when the two solutions above are equal, implying that the quantity under the square root sign is zero. This requires solving a quadratic equation for 
This gives
If we denote the angle whose tangent is y/x by α, then
This implies
In other words, the launch should be at the angle halfway between the target and Zenith (vector opposite to Gravity)
Total Path Length of the Trajectory[edit]
The length of the parabolic arc traced by a projectile L, given that the height of launch and landing is the same and that there is no air resistance, is given by the formula:
where 


.
Trajectory of a projectile with air resistance[edit]
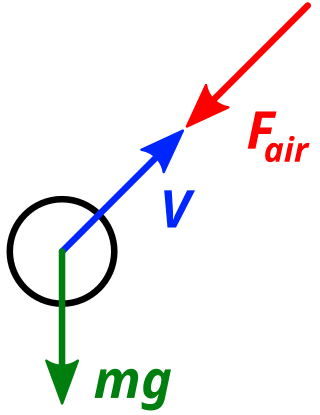
Air resistance creates a force that (for symmetric projectiles) is always directed against the direction of motion in the surrounding medium and has a magnitude that depends on the absolute speed: 




Free body diagram of a body on which only gravity and air resistance acts
The free body diagram on the right is for a projectile that experiences air resistance and the effects of gravity. Here, air resistance is assumed to be in the direction opposite of the projectile’s velocity: 
Trajectory of a projectile with Stokes drag[edit]
Stokes drag, where 


in which the two cartesian components become completely independent, and thus easier to solve.[5]
Here, 




|
Derivation of horizontal position |
|---|
|
The relationships that represent the motion of the particle are derived by Newton’s Second Law, both in the x and y directions. This implies that:
and
Solving (1) is an elementary differential equation, thus the steps leading to a unique solution for vx and, subsequently, x will not be enumerated. Given the initial conditions
|
(1b)
|
Derivation of vertical position |
|---|
|
While (1) is solved much in the same way, (2) is of distinct interest because of its non-homogeneous nature. Hence, we will be extensively solving (2). Note that in this case the initial conditions are used
This first order, linear, non-homogeneous differential equation may be solved a number of ways; however, in this instance, it will be quicker to approach the solution via an integrating factor
And by integration we find:
Solving for our initial conditions:
With a bit of algebra to simplify (3a): |
(3b)
.
Trajectory of a projectile with Newton drag[edit]
Trajectories of a skydiver in air with Newton drag
The most typical case of air resistance, for the case of Reynolds numbers above about 1000 is Newton drag with a drag force proportional to the speed squared, 


Unfortunately, the equations of motion can not be easily solved analytically for this case. Therefore, a numerical solution will be examined.
The following assumptions are made:
- Constant gravitational acceleration
- Air resistance is given by the following drag formula,
-
- Where:
-
-
- FD is the drag force
- c is the drag coefficient
- ρ is the air density
- A is the cross sectional area of the projectile
- μ = k/m = cρA/(2m)
-
Special cases[edit]
Even though the general case of a projectile with Newton drag cannot be solved analytically, some special cases can. Here we denote the terminal velocity in free-fall as 

- Near-horizontal motion: In case the motion is almost horizontal,
, such as a flying bullet, the vertical velocity component has very little influence on the horizontal motion. In this case:[7]
-
- The same pattern applies for motion with friction along a line in any direction, when gravity is negligible. It also applies when vertical motion is prevented, such as for a moving car with its engine off.
- Vertical motion upward:[7]
-
- Here
- and
- where
is the initial upward velocity at
and the initial position is
.
- A projectile can not rise longer than
vertically before it reaches the peak.
- Vertical motion downward:[7]
-
- After a time
, the projectile reaches almost terminal velocity
.
Numerical solution[edit]
A projectile motion with drag can be computed generically by numerical integration of the ordinary differential equation, for instance by applying a reduction to a first-order system. The equation to be solved is
.
This approach also allows to add the effects of speed-dependent drag coefficient, altitude-dependent air density and position-dependent gravity field.
Lofted trajectory[edit]
A special case of a ballistic trajectory for a rocket is a lofted trajectory, a trajectory with an apogee greater than the minimum-energy trajectory to the same range. In other words, the rocket travels higher and by doing so it uses more energy to get to the same landing point. This may be done for various reasons such as increasing distance to the horizon to give greater viewing/communication range or for changing the angle with which a missile will impact on landing. Lofted trajectories are sometimes used in both missile rocketry and in spaceflight.[8]
Projectile motion on a planetary scale[edit]
Projectile trajectory around a planet, compared to the motion in a uniform field
When a projectile without air resistance travels a range that is significant compared to the earth’s radius (above ≈100 km), the curvature of the earth and the non-uniform Earth’s gravity have to be considered. This is for example the case with spacecraft or intercontinental projectiles. The trajectory then generalizes from a parabola to a Kepler-ellipse with one focus at the center of the earth. The projectile motion then follows Kepler’s laws of planetary motion.
The trajectories’ parameters have to be adapted from the values of a uniform gravity field stated above. The earth radius is taken as R, and g as the standard surface gravity. Let 
Total range d between launch and impact:
Maximum range of a projectile for optimum launch angle (
with
, the first cosmic velocity
Maximum height of a projectile above the planetary surface:
Maximum height of a projectile for vertical launch (
with
, the second cosmic velocity
Time of flight:
See also[edit]
- Equations of motion
Notes[edit]
References[edit]
- ^ Galileo Galilei, Two New Sciences, Leiden, 1638, p.249
- ^ Nolte, David D., Galileo Unbound (Oxford University Press, 2018) pp. 39-63.
- ^ Tatum (2019). Classical Mechanics (PDF). pp. ch. 7.
- ^ Stephen T. Thornton; Jerry B. Marion (2007). Classical Dynamics of Particles and Systems. Brooks/Cole. p. 59. ISBN 978-0-495-55610-7.
- ^ Atam P. Arya; Atam Parkash Arya (September 1997). Introduction to Classical Mechanics. Prentice Hall Internat. p. 227. ISBN 978-0-13-906686-3.
- ^ Rginald Cristian, Bernardo; Jose Perico, Esguerra; Jazmine Day, Vallejos; Jeff Jerard, Canda (2015). «Wind-influenced projectile motion». European Journal of Physics. 36 (2): 025016. Bibcode:2015EJPh…36b5016B. doi:10.1088/0143-0807/36/2/025016. S2CID 119601402.
- ^ a b c Walter Greiner (2004). Classical Mechanics: Point Particles and Relativity. Springer Science & Business Media. p. 181. ISBN 0-387-95586-0.
- ^ Ballistic Missile Defense, Glossary, v. 3.0, US Department of Defense, June 1997.
для общего образования. отсюда
оставил целиком. а важное выделил красным.
самое важное
1) мина летит с дозвуковой скоростью по крутой траектории. Это значит, что можно услышать выстрел и характерный свистящий звук от мины до её взрыва.
мина 82мм на 6км летит 30-60 сек (нач. скорость 100-200м/с) отсюда
мина 120мм на 6км летит 22-50 сек (нач.скорость 119 — 270 м/с) отсюда и отсюда
звук выстрела на 6км дойдет за 18 сек (скорость звука 330 м/с).
итого времени на реакцию 4-12-32-42 секунд (неточно, т.к скорость зависит от заряда). ИТОГО секунд 5-10 есть.
2) определить откуда стреляли можно
3) ДК Куйбышева, судя по всему, обстреляли миной 82 мм (или менее)
4) максимальная дальность стрельбы миномёта не больше 6-7 км (независимо от калибра). Реальная (прицельная) 4-6 км.
ВЫЖИТЬ ПОД МИНОМЕТНЫМ ОБСТРЕЛОМ.
Характеристики минометов и мин, правила поведения под обстрелом.
82-мм мина: Радиус действительного поражения
лежащих
целей 82-мм осколочной мины не менее
18 м
. При этом на площади поражения трава выкашивается полностью. Радиус капитального поражения ростовых целей – 30 м при обязательном поражении цели 2-3 осколками. Разлет отдельных осколков может составлять до 100-150 метров.
82-мм мина в состоянии разрушить лишь легкое перекрытие, например, козырек из жердей над окопом.
Воронка при ее разрыве, даже в том случае, когда мина уйдет в грунт на самую выгодную глубину, будет невелика: диаметром 1 метр и глубиной около 50-60 сантиметров. Но обычно такая воронка не получается, потому что 82- миллиметровая мина не предназначена для стрельбы на разрушение, а рассчитана лишь на осколочное действие, и она разрывается раньше, чем проникнет в грунт…
82-мм минометы – оружие не особо дальнобойное, но очень распространенное. Максимальная дальность стрельбы – можно до 4 километр. Минимальная дальность стрельбы — 85-100 метров. Поэтому в целях маскировки миномет и боекомплект обычно переносят на руках. Миномет весит больше 40 килограммов, стандартный ящик с 10 минами – больше 30 (итого 70 кг!!!). Поэтому минометные обстрелы обычно внезапные и непродолжительные: опытный расчет делает десять выстрелов за считанные секунды, и последняя мина выходит из ствола еще до взрыва первой. После этого минометчики немедленно разбирают миномет (до минуты) и меняют позицию, чтобы уйти от ответного огня.
120-мм мина: Радиус действительного поражения лежащих целей осколочной мины не мене 25м. Радиус капитального поражения ростовых целей – 60м. Разлет отдельных осколков может доходить до 200-250 метров. Вес разрывного заряда в 16 килограмовой 120-мм осколочно-фугасной мины 3,93 килограмма. Фугасная мина, проникая на самую выгодную глубину, создает воронку диаметром в 3-4 метра и глубиной около 1 метра. Эта мина хорошо разрушает окопы и легкие блиндажи. Попадание одной мины уничтожает стандартную двухкомнатную квартиру. А три, четыре мины — обрушивают перекрытие этажа панельного дома. Так же тяжелые осколки данной мины, могут серьезно повредить БТР, БМП и другую легкую бронетехнику с противопульным бронированием. При прямом попадании вывести из строя.
120-мм миномет может бить на 7,2 км. Эффективно на дальность до 7 км. Минимальная дальность (мертвая зона) – 480 метров. Скорострельность – 10-15 выстрелов. Возимый боекомплект — 80 мин.
Буксируемое или самоходное 120-мм нарезное орудие-миномет типа «Нона» (на вооружении 25 ВДБр) Скорострельность – до 11 выстрелов в минуту. Применяется против живой силы, расположенной на открытой местности, в окопах или легких укрытиях.
Боеприпасы “Ноны”: В основной боекомплект орудия входят осколочно-фугасные снаряды 3ОФ49 с контактным взрывателем и радиовзрывателем. Снаряды обладают начальной скоростью на полном заряде 367 м/с и максимальной дальностью стрельбы в 8,855 км. При установке контактного взрывателя на осколочное действие во время разрыва снаряд 3ОФ49 образует около 3500 убойных осколков массой от 0,5 до 15 г, обладающих начальной скоростью около 1800 м/с. Приведённая площадь поражения открыто расположенной живой силы в положении «стоя» составляет 2200 м², бронепробиваемость гомогенной стальной брони составляет 12 мм на расстоянии от 7 до 10 м от эпицентра разрыва снаряда. При использовании радиовзрывателя АР-5 эффективность поражения открыто расположенной живой силы увеличивается от 2 до 3 раз. При установке контактного взрывателя на фугасное действие снаряд 3ОФ49 способен образовывать воронки до 5 м в диаметре и до 2 метров глубиной. Также “Нона” лупит всеми типами 120-мм минометных мин.
У миномета есть несколько особенностей, которые надо знать обязательно. Во-первых, мина летит с дозвуковой скоростью по крутой траектории. Это значит, что можно услышать выстрел и характерный свистящий звук от мины до ее взрыва. Опытные бойцы по звуку определяют, в какую сторону она летит, приближается ( звук меняется от низких частот к высоким) или уже удаляется при перелете. В боевых условиях такие навыки нужно приобретать как можно быстрее.
Во-вторых, мина взрывается при ударе о землю, и осколки разлетаются вверх и в стороны. Поэтому автомобиль или стоящий человек – очень уязвимая цель. Если же боец в момент взрыва мины лежит, вероятность попадания в него осколками резко уменьшается. Поэтому, услышав звук приближающейся мины (или предупреждающий крик опытного товарища), немедленно падайте на землю и вжимайтесь в нее посильнее, закрывая голову руками.
Осколки 82-мм мины – легкие и очень «дурные». При взрыве трехкилограммовой мины образуются 400-600 осколков. Любая преграда – кирпич, дерево, бетонный столб, – может непредсказуемо изменить направление их полета. По этой же причине осколки мины плохо пробивают более-менее серьезные препятствия. Каменная стена, бруствер, мешок с песком, ствол упавшего дерева, каска, бронежилет – все это может помочь.
Если противник ведет не прицельный обстрел по площади, то желательно не высовываться минут 5 — 10, пакет уничтожения обычно 60- 80 мин по квадрату.
Иногда минометчики выпускают одну пристрелочную мину (дымовую или зажигательную) в сторону цели и по месту ее разрыва, вводят поправки и включают беглый огонь всей батареей на поражение. Так что после первого разрыва в стороне, есть немного времени найти укрытие и залечь.
По опыту, из миномета обстреливают «сериями»: 6-8 выстрелов, пауза в несколько минут, затем снова 6-8 выстрелов на добитие. Обычно таких серий бывало не больше трех. Возможен обстрел из одного, двух или трех минометов (три минометных расчета входят в состав взвода).
Во время обстрела даже не думайте вставать. Лежите там, где упали. Во время паузы можно осмотреть местность, переместиться в щель, яму, воронку. Чем ниже вы будете лежать, тем больше шансов пережить обстрел без последствий. Окопы, блиндажи, сооружения из бетонных блоков, прочные кирпичные стены – вполне надежная защита от миномета. Даже в чистом поле можно придумать укрытие.
Не очень хорошая идея пересидеть обстрел в редкой посадке или кустах. Взрыватель мины сработает при ударе об ветки и получиться воздушный подрыв мины, что увеличит зону поражения осколками.
В паузе будьте готовы к началу следующей «серии» обстрела, о приближении которой вас предупредит все тот же свистящий звук.
Итак, основные правила выживания при минометном обстреле:
1. Прислушивайтесь к звукам летящих мин, научитесь их распознавать и анализировать.
2. При обстреле немедленно падайте и вжимайтесь в землю. Научитесь делать это до того, как мины начнут падать – это в ваших интересах.
4. Не забудьте открыть рот, это спасет ваши барабанные перепонки.
5. Что бы ни случилось, ни в коем случае нельзя приподниматься и тем более вставать. Не пытайтесь убежать из зоны обстрела – мины и осколки все равно быстрее вас. Дождитесь, пока не прозвучит пример 8-10 разрывов, потом подождите хотя бы три минуты, после чего быстро меняйте позицию и уходите в укрытие. Даже если кому-то рядом нужна помощь – оказывайте ее после обстрела и в укрытии, иначе помощь, скорее всего, скоро понадобится и вам.
6. Используйте искусственные и естественные укрытия и складки местности. Спрятаться в них можно в перерывах между сериями выстрелов.
7. Передвигайтесь только ползком. Если вы попали под обстрел в поле и переждали его, покидайте зону обстрела ползком дабы не быть замеченными и не вызвать повторный обстрел.
8. Если Вы находитесь в зоне, где возможен минометный обстрел, не снимайте бронежилет и каску, – если они у вас, конечно, есть. Бронежилеты третьего или четвертого класса останавливают минометные осколки вполне надежно. Даже простенький жилет второго класса и шлем старого советского образца не будут лишними.
9.Бывает что часть мин не разрывается (мягкий грунт, взрыватель не сработал) и нагло торчат хвостовиками из земли. Ни в коем случае их не трогайте, не доставайте и не буцайте. Вероятность взрыва крайне высока.
10. Копайте окопы и стройте блендажи с крепкими перекрытиями. Пути сообщений должны быть зигзагообразными. В случае попадания мины в траншею, разлет осколков будет ограничен только прямым сегментом.
11. Не стесняйтесь тренироваться и отрабатывать свои действия в случае обстрела заранее. Помните: тяжело в учении, легко в зоне поражения.
12. Если вы попали под минометный обстрел во время марша на “броне”, ныряйте во внутрь. Задача водителя БТР на полной скорости выйти из зоны огня. Остановившись и спешившись, вы превращаетесь в идеальную, неподвижную мишень для минометов.
13. Держите под прицелом снайперов места, где может быть корректировщик минометов. Это как правило развалины, высокие дома и деревья в зоне прямой видимости от вашего местоположения, с которых открывается хороший обзор местности. Человек с биноклем и рацией (телефоном)-цель №1.
Как определить, откуда стрелял миномет или орудие?
По характеру воронки от снаряда или мины можно установить, откуда велась стрельба. Дело в том, что снаряд падает под углом, а не строго вертикально, он разрывается, находясь как бы на боку, поэтому воронка неравномерна. Сторона, обращенная к точке выстрела, будет более пологой, чем противоположная. Осколков в земле больше с той стороны, откуда прилетел снаряд, так как большая часть
снарядов
осколков с противоположной стороны ушли в воздух при взрыве. Обычно после удаления рыхлого грунта можно найти след снаряда в земле и определить общее направление стрельбы.
Определить дальность до места, откуда был произведен выстрел, можно намного точнее, если определить какой боеприпас образовал воронку. Измерив угол падения снаряда, можно, пользуясь таблицами для стрельбы, определить, с какой дальности производился выстрел. Угол измеряется так: осторожно удаляется разрыхленная взрывом земля, находится центр ее углубления (лунка). Берется палка, которая кладется на края воронки, освобожденные от насыпанного взрывом грунта (так определяется плоскость грунта). После этого посередине отлогого склона воронки (того, что со стороны выстрела) вбивается колышек, доходящий до плоскости грунта. Таким образом мы определяем усредненную точку соприкосновения снаряда с грунтом, после чего от лунки до этой точки проводим прямую – проще всего, накладываем палку или рейку, получая «траекторию» движения снаряда на последнем метре полета. Измерив угол падения, мы можем определить угол вылета, а, следовательно, дальность по таблицам для стрельбы.
Когда впервые попадаешь под огонь из миномета, может показаться, что хуже ничего быть не может. На самом деле – может. После недельного обстрела «Градами» стрельба из миномета представляется скорее раздражающим, чем устрашающим фактором.
На картинках: №1- 120 мм миномет; №2- след взрыва 120-мм мины в траве: №3- Зоны поражения минометных мин из американского военного учебника с % поражения на дистанции; №4- след от взрыва 82-мм мины на асфальте.
Сведения из внешней баллистики
25. Внешняя баллистика — это наука, изучающая движение пули (гранаты) после прекращения действия на нее пороховых газов.
Вылетев из канала ствола под действием пороховых газов, пуля (граната) движется по инерции. Граната, имеющая реактивный двигатель, движется по инерции после истечения газов из реактивного двигателя.
Траектория и её элементы
26. Траекторией называется кривая линия, описываемая центром тяжести пули (гранаты) в полете (рис. 5).
Пуля (граната) при полете в воздухе подвергается действию двух сил: силы тяжести и силы сопротивления воздуха. Сила тяжести заставляет пулю (гранату) постепенно понижаться, а сила сопротивления воздуха непрерывно замедляет движение пули (гранаты) и стремится опрокинуть ее.
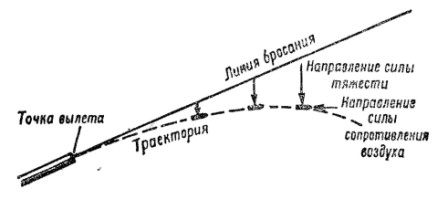
Рис. 5. Траекторя пули (вид сбоку)
В результате действия этих сил скорость полета пули (гранаты) постепенно уменьшается, а ее траектория представляет собой по форме неравномерно изогнутую кривую линию.
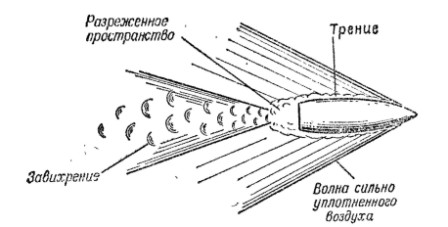
Рис. 6. Образование силы сопратевления воздуха
27. Сопротивление воздуха полету пули (гранаты) вызывается тем, что воздух представляет собой упругую среду, поэтому на движение в этой среде затрачивается часть энергии пули (гранаты).
Сила сопротивления воздуха вызывается тремя основными причинами (рис. 6): трением воздуха, образованием завихрений и образованием баллистической волны,
28. Частицы воздуха, соприкасающиеся с движущейся пулей (гранатой), вследствие внутреннего сцепления (вязкости) и сцепления с ее поверхностью создают трение и уменьшают скорость полета пули (гранаты).
29. Примыкающий к поверхности пули (гранаты) слой воздуха, в котором движение частиц изменяется от скорости пули (гранаты) до нуля, называется пограничным слоем. Этот слой воздуха, обтекая пулю, отрывается от ее поверхности и не успевает сразу же сомкнуться за донной частью.
За донной частью пули образуется разреженное пространство, вследствие чего появляется разность давлений на головную и донную части. Эта разность создает силу, направленную в сторону, обратную движению пули, и уменьшающую скорость ее полета. Частицы воздуха, стремясь заполнить разрежение, образовавшееся за пулей, создают завихрение.
30. Пуля (граната) при полете сталкивается с частицами воздуха и заставляет их колебаться. Вследствие этого перед пулей (гранатой) повышается плотность воздуха, и образуются звуковые волны. Поэтому полет пули (гранаты) сопровождается характерным звуком. При скорости полета пули (гранаты), меньшей скорости звука, образование этих волн оказывает незначительное влияние на ее полет, так как волны распространяются быстрее скорости полета пули (гранаты). При скорости полета пули, большей скорости звука, от набегания звуковых воли друг на друга создается волна сильно уплотненного воздуха — баллистическая волна, замедляющая скорость полета пули, так как пуля тратит часть своей энергии па создание этой волны.
31. Равнодействующая (суммарная) всех сил, образующихся вследствие влияния воздуха на полет пули (гранаты), составляет силу сопротивления воздуха. Точка приложения силы сопротивления называется центром сопротивления.
Действие силы сопротивления воздуха на полет пули (гранаты) очень велико; оно вызывает уменьшение скорости и дальности полета пули (гранаты). Например, пуля обр. 1930 г. при угле бросания 15° и начальной скорости 800 м/с в безвоздушном пространстве полетела бы на дальность 32620 м; дальность полета этой пули при тех же условиях, но при наличии сопротивления воздуха равна лишь 3900 м.
32. Величина силы сопротивления воздуха зависит от скорости полета, формы и калибра пули (гранаты), а также от ее поверхности и плотности воздуха.
Сила сопротивления воздуха возрастает с увеличением скорости полета пули, ее калибра и плотности воздуха.
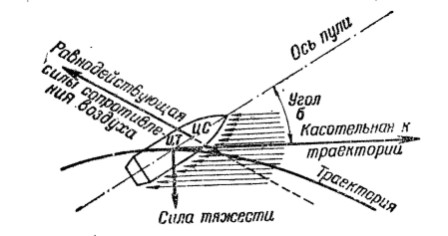
Рис. 7. Действие силы сопротевления воздуха на полёт пули:
ЦТ — центр тяжести; ЦС — центр сопротивления воздуха
При сверхзвуковых скоростях полета пули, когда основной причиной сопротивления воздуха является образование уплотнения воздуха перед головной частью (баллистической волны), выгодны пули с удлиненной остроконечной головной частью. При дозвуковых скоростях полета гранаты, когда основной причиной сопротивления воздуха является образование разреженного пространства и завихрений, выгодны гранаты с удлиненной и суженной хвостовой частью.
Чем глаже поверхность пули, тем меньше сила трения и сила сопротивления воздуха.
Разнообразие форм современных пуль (гранат) во многом определяется необходимостью уменьшить силу сопротивления воздуха.
33. Под действием начальных возмущений (толчков) в момент вылета пули из канала ствола между осью пули и касательной к траектории образуется угол (б) и сила сопротивления воздуха действует не вдоль оси пули, а под углом к ней, стремясь не только замедлить движение пули, но и опрокинуть ее (рис. 7).
Для того чтобы пуля не опрокидывалась под действием силы сопротивления воздуха, ей придают с помощью нарезов в канале ствола быстрое вращательное движение.
Например, при выстреле из автомата Калашникова скорость вращения пули в момент вылета из канала ствола равна около 3000 оборотов в секунду.
При полете быстро вращающейся пули в воздухе происходят следующие явления. Сила сопротивлении воздуха стремится повернуть пулю головной частью вверх и назад.
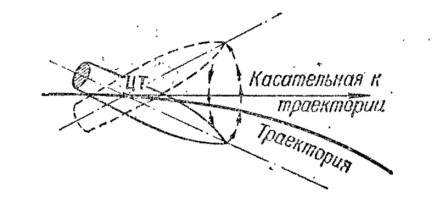
Рис. 8. Медленное конисеское движений пули
Но головная часть пули в результате быстрого вращения согласно свойству гироскопа стремится сохранить приданное положение и отклониться не вверх, а весьма незначительно в сторону своего вращения под прямым углом к направлению действия силы сопротивлении воздуха, т. е, вправо. Как только головная часть пули отклонится вправо, изменится направление действия силы сопротивления воздуха — она стремится повернуть головную часть пули в право и назад, но поворот головной части пули произойдет не вправо, а вниз и т. д. Так как действие силы сопротивления воздуха непрерывно, а направление ее относительно пули меняется с каждым отклонением оси пули, то головная часть пули описывает окружность, а ее ось — конус с вершиной в центре тяжести. Происходит так называемое медленное коническое, или прецессионное движение, и пуля летит головной частью вперед, т. е. как бы следит за изменением кривизны траектории (рис. 8).
34, Ось медленного конического движения несколько отстает от касательной к траектории (располагается выше последней). Следовательно, пуля с потоком воздуха сталкивается больше нижней частью, и ось медленного конического движения отклоняется в сторону вращения (в право при правой нарезке ствола). Отклонение пули от плоскости стрельбы в сторону ее вращения называется деривацией (рис. 9).
Таким образом, причинами деривации являются: вращательное движение пули, сопротивление воздуха и понижение под действием силы тяжести касательной к траектории.

Рис. 9. Деревация (вид траектории сверху)
При отсутствии хотя бы одной из этих причин деривации не будет.
В таблицах стрельбы деривация дается как поправка направления в тысячных. Однако при стрельбе из стрелкового оружия величина деривации незначительная (например, на дальности 500 м она не превышает 0,1 тысячной) и ее влияние на результаты стрельбы практически не учитывается.
35. Устойчивость гранаты на полете обеспечивается наличием стабилизатора, который позволяет перенести центр сопротивления воздуха назад, за центр тяжести гранаты (рис. 10). Вследствие этого сила сопротивления воздуха поворачивает ось гранаты касательной к траектории, заставляя гранату двигаться головной частью вперед.
Для улучшения кучности некоторым гранатам придают за счет истечения газов медленное вращение.
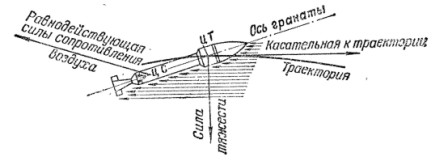
Рис. 10. Действие силы сопротивления воздуха на полёт гранаты
Вследствие вращения гранаты моменты сил, отклоняющие ось гранаты, действуют последовательно в разные стороны, поэтому кучность стрельбы улучшается.
38. Для изучения траектории пули (гранаты) приняты следующие определения (рис. 11).
Центр дульного среза ствола называется точкой вылета. Точка вылета является началом траектории.
Горизонтальная плоскость, проходящая через точку вылета, называется горизонтом оружия. На чертежах, изображающих оружие и траекторию сбоку, горизонт оружия имеет вид горизонтальной линии. Траектория дважды пересекает горизонт оружия: в точке вылета и в точке падения.
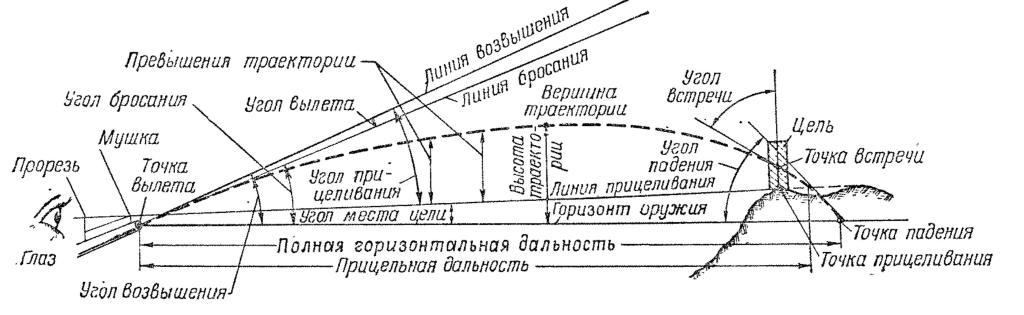
Рис. 11. Элементы траектории
Прямая линия, являющаяся продолжением оси канала ствола наведенного оружия, называется линией возвышения.
Вертикальная плоскость, проходящая через линию возвышения, называется плоскостью стрельбы.
Угол, заключенный между линией возвышения и горизонтом оружия, называется углом возвышения (φ).
Если этот угол отрицательный, то он называется углом склонения (снижения).
Прямая линия являющаяся продолжением оси канала ствола в момент вылета пули, называется линией бросания.
Угол, заключенный между линией бросания и горизонтом оружия, называется углом бросания (0О).
Угол, заключенный между линией возвышения и линией бросания, называется углом вылета (у).
Точка пересечения траектории с горизонтом оружия называется точкой падения.
Угол, заключенный между касательной к траектории в точке падения и горизонтом оружия, называется углом падения (Ос).
Расстояние от точки вылета до точки падения называется полной горизонтальной дальностью (X).
Скорость пули (гранаты) в точке падения называется окончательной скоростью (vc).
Время движения пули (гранаты) от точки вылета до точки падения называется полным временем полета (Г).
Наивысшая точка траектории называется вершиной траектории.
Кратчайшее расстояние от вершины траектории до горизонта оружия называется высотой траектории (У).
Часть траектории от точки вылета до вершины называется восходящей ветвью; часть траектории от вершины до точки падения называется нисходящей ветвью траектории.
Точка на цели или вне ее, в которую наводится оружие, называется точкой прицеливания (наводки).
Прямая линия, проходящая от глаза стрелка через середину прорези прицела (на уровне с ее краями) и вершину мушки в точку прицеливания, называется линией прицеливания.
Угол, заключенный между линией возвышения и линией прицеливания, называется углом прицеливания (а).
Угол, заключенный между линией прицеливания и горизонтом оружия, называется углом места цели (ε). Угол места цели считается положительным (+), когда цель выше горизонта оружия, и отрицательным (—), когда цель ниже горизонта оружия. Угол места цели может быть определен с помощью приборов или по формуле тысячной:
где ε угол места цели в тысячных;
В — превышение цели над горизонтом оружия в метрах;
Д — дальность стрельбы в метрах.
Расстояние от точки вылета до пересечения траектории с линией прицеливания называется прицельной дальностью (Дп).
Кратчайшее расстояние от любой точки траектории до линии прицеливания называется превышением траектории над линией прицеливания.
Прямая, соединяющая точку вылета с целью, называется линией цели. Расстояние от точки вылета до цели, по линии цели называется наклонной дальностью. При стрельбе прямой наводкой линия цели практически совпадает с линией прицеливания, а наклонная дальность — q прицельной дальностью.
Точка пересечения траектории с поверхностью цели (земли, преграды) называется точкой встречи.
Угол, заключенный между касательной к траектории и касательной к поверхности цели (земли, преграды) в точке встречи, называется углом встречи (μ). За угол встречи принимается меньший из смежных углов, измеряемый от 0 до 90°.
37. Траектория пули в воздухе имеет следующие свойства:
— нисходящая ветвь короче и круче восходящей;
— угол падения больше угла бросания;
— окончательная скорость пули меньше начальной;
— наименьшая скорость полета пули при стрельбе под большими углами бросания — на нисходящей ветви траектории, а при стрельбе под небольшими углами бросания — в точке падения;
— время движения пули по восходящей ветви траектории меньше, чем по нисходящей;
— траектория вращающейся пули вследствие понижения пули под действием силы тяжести и деривации представляет собой линию двоякой кривизны.
38. Траекторию гранаты в воздухе можно разделить на два участка (рис. 12): активный — полет гранаты под действием реактивной силы (от точки вылета до точки, где действие реактивной силы прекращается) и пассивный полет гранаты по инерции. Форма траектории гранаты примерно такая же, как и у пули.
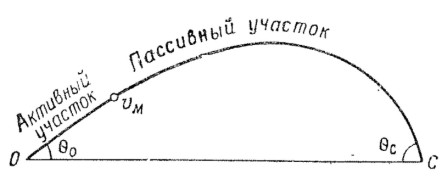
Рис. 12. Траектория гранаты (вид сбоку)