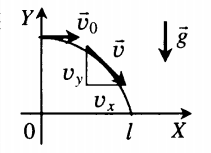
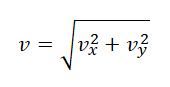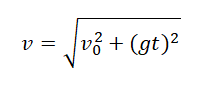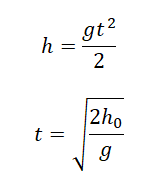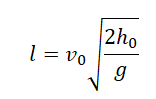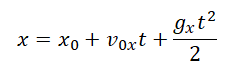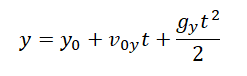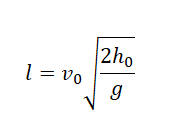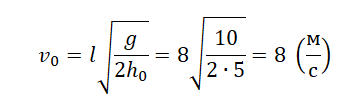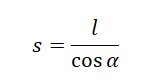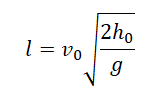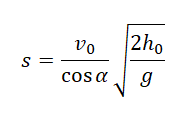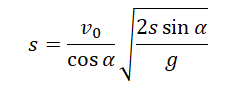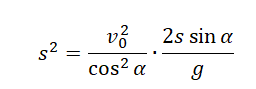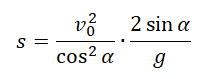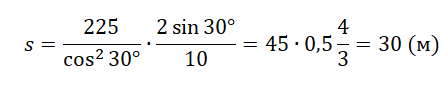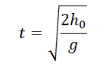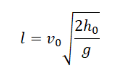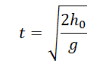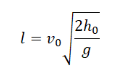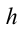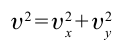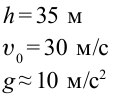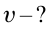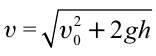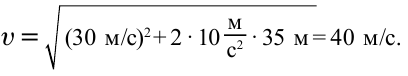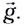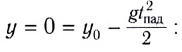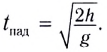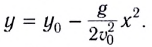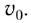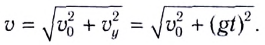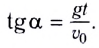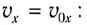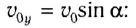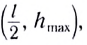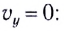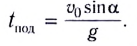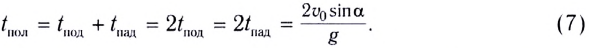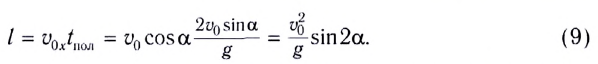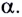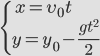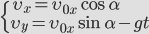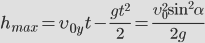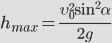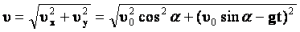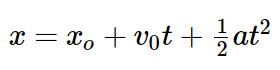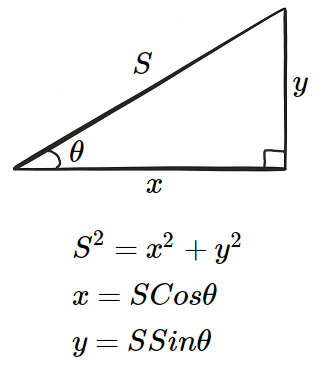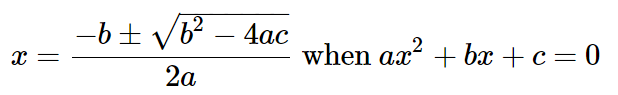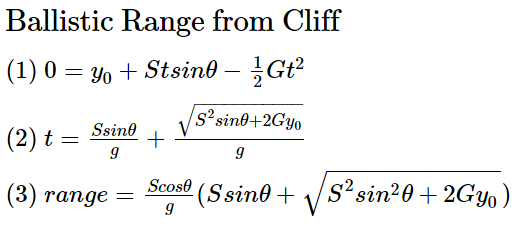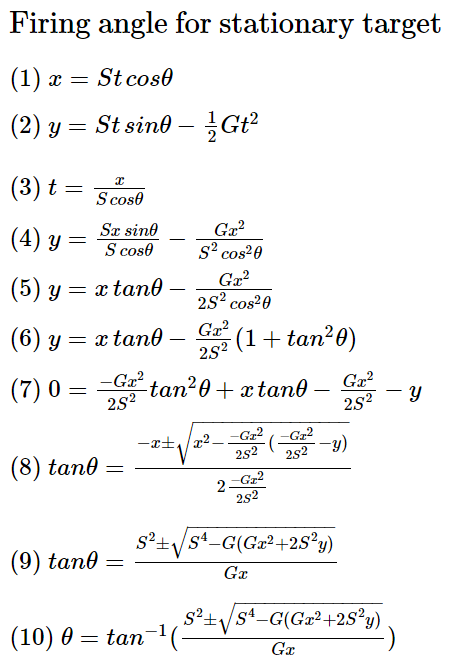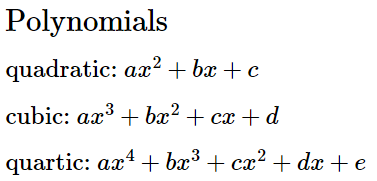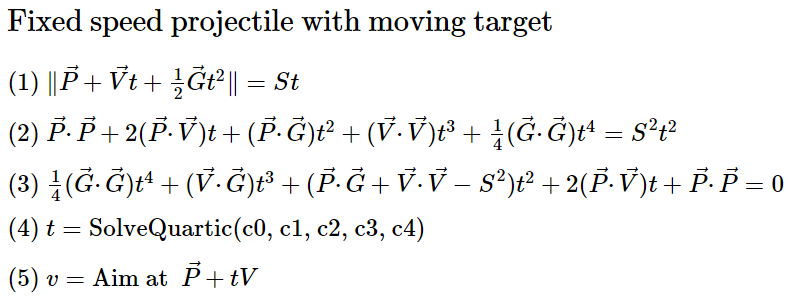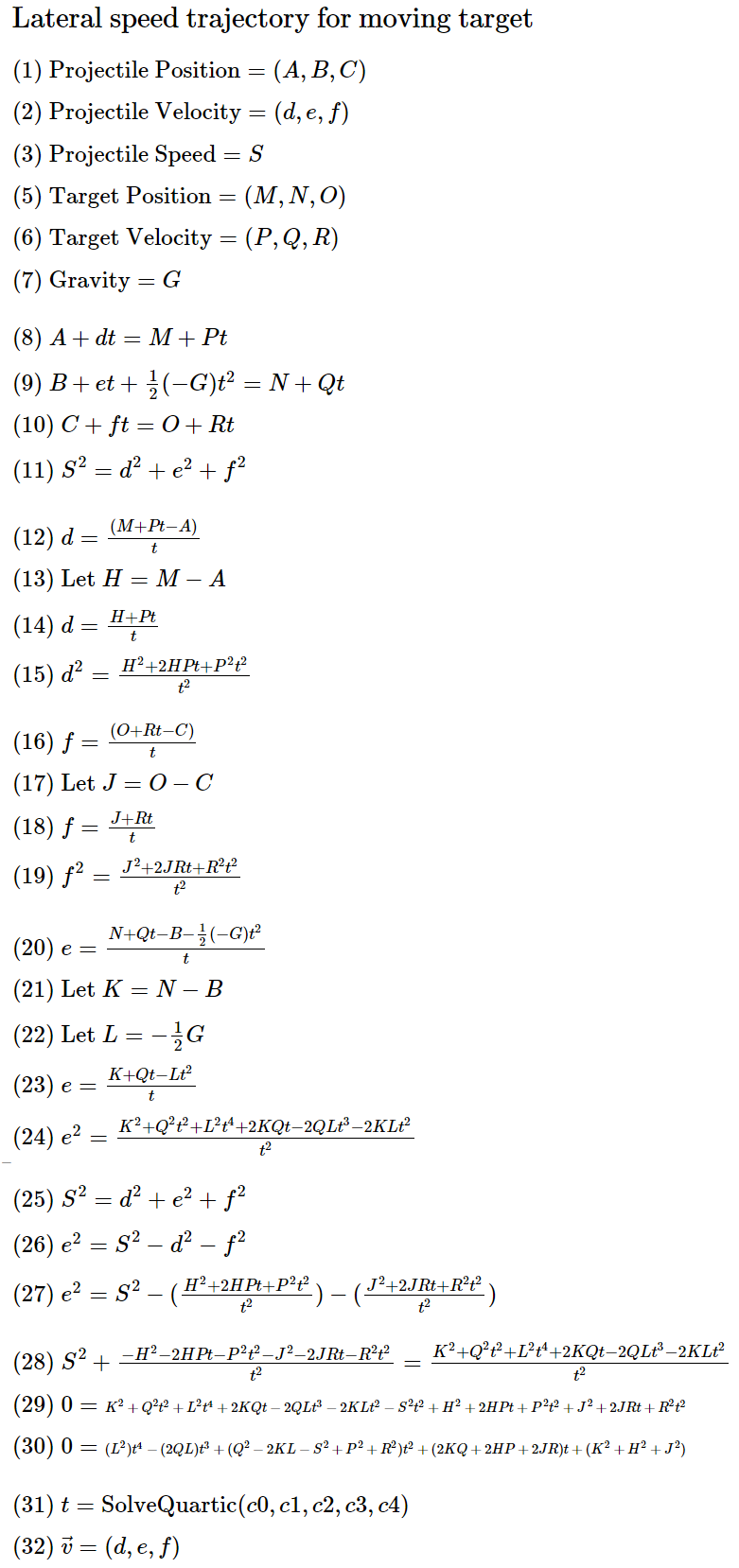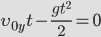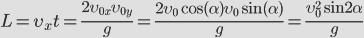Если тело бросить горизонтально с некоторой высоты, оно будет одновременно падать и двигаться вперед. Это значит, что оно будет менять положение относительно двух осей: ОХ и ОУ. Относительно оси ОХ тело будет двигаться с постоянной скоростью, а относительно ОУ — с постоянным ускорением.
Кинематические характеристики движения
Важные факты!
Графически движение горизонтально брошенного тела описывается следующим образом:
- Вектор скорости горизонтально брошенного тела направлен по касательной к траектории его движения.
- Проекция начальной скорости на ось ОХ равна v0: vox = v0. Ее проекция на ось ОУ равна нулю: voy = 0.
- Проекция мгновенной скорости на ось ОХ равна v0: vx = v0. Ее проекция на ось ОУ равна нулю: vy = –gt.
- Проекция ускорения свободного падения на ось ОХ равна нулю: gx = 0. Ее проекция на ось ОУ равна –g: gy = –g.
Модуль мгновенной скорости в момент времени t можно вычислить по теореме Пифагора:
Подставив в эту формулу значения проекций мгновенной скорости в момент времени t, получим:
Минимальная скорость в течение всего времени движения равна начальной скорости: vmin = v0.
Максимальной скорости тело достигает в момент приземления. Поэтому максимальной скоростью тела в течение всего времени движения является его конечная скорость: vmax = v.
Время падения — время, в течение которого перемещалось тело до момента приземления. Его можно выразить через формулу высоты при равноускоренном прямолинейном движении:
h0 — высота, с которой тело бросили в горизонтальном направлении.
Дальность полета — перемещение тела относительно ОХ. Обозначается буквой l. Так как относительно ОХ тело движется с постоянной скоростью, для вычисления дальности полета можно использовать формулу перемещения при равномерном прямолинейном движении:
l = sx = v0tпад
Выразив время падения через высоту и ускорение свободного падения, формула для определения дальности полета получает следующий вид:
Горизонтальное смещение тела — смещение тела вдоль оси ОХ. Вычислить горизонтальное смещение тела в любой момент времени t можно по формуле координаты x:
Учитывая, что x0 = 0, и проекция ускорения свободного падения на ось ОХ тоже равна нулю, а проекция начальной скорости есть модуль этой скорости, данная формула принимает вид:
x = v0t
Мгновенная высота — высота, на которой находится тело в выбранный момент времени t. Она вычисляется по формуле координаты y:
Пример №1. Из окна, расположенного 5 м от земли, горизонтально брошен камень, упавший на расстоянии 8 м от дома. С какой скоростью был брошен камень?
Так как нам известна высота места бросания и дальность полета, начальную скорость тела можно вычислить по формуле:
Выразим начальную скорость и вычислим ее:
Горизонтальный бросок тела с горы
Горизонтальный бросок тела с горы — частный случай горизонтального броска. От него он отличается увеличенным расстоянием между местом бросания и местом падения. Это увеличение появляется потому, что плоскость находится под наклоном. И чем больше этот наклон, тем больше времени требуется телу, чтобы приземлиться.
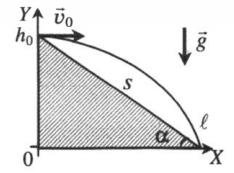
График горизонтального броска тела с горы
α — угол наклона плоскости к горизонту, s — расстояние от места бросания до места падения
Дальность полета — смещение тела относительно оси ОХ от места бросания до места падения. Она равна произведению расстояния от места бросания до места падения и косинуса угла наклона плоскости к горизонту:
l = s • cosα
Начальная высота — высота, с которой было брошено тело. Обозначается h0. Начальная высота равна произведению расстояния от места бросания до места падения и синусу угла наклона плоскости к горизонту:
h0 = s sinα
Пример №2. На горе с углом наклона 30о бросают горизонтально мяч с начальной скоростью 15 м/с. На каком расстоянии от точки бросания вдоль наклонной плоскости он упадет?
Выразим это расстояние через дальность полета:
Дальность полета выражается по формуле:
Подставим ее в формулу для вычисления расстояния от точки бросания до точки падения:
Выразим с учетом формулы начальной высоты:
Преобразуем:
Поделим обе части выражения на общий множитель s:
Подставим известные значения:
Задание EF18083
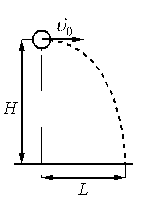
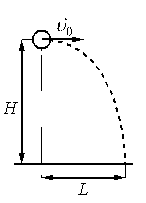
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
В другом опыте на этой же установке шарик массой 2m бросают со скоростью 2υ0.
Что произойдёт при этом с временем полёта, дальностью полёта и ускорением шарика? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости и массы.
- Определить характер изменения физической величины при увеличении начальной скорости и массы шарика.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости и массы тела. Поэтому оно при увеличении начальной скорости и массы вдвое никак не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет увеличена вдвое, дальность полета тоже увеличится (вдвое). От массы дальность полета никак не зависит.
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 313.
Ответ: 313
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18048
Шарик, брошенный горизонтально с высоты H с начальной скоростью υ0, за время t пролетел в горизонтальном направлении расстояние L (см. рисунок).
Что произойдёт с временем полёта, дальностью полёта и ускорением шарика, если на этой же установке уменьшить начальную скорость шарика в 2 раза? Сопротивлением воздуха пренебречь. Для каждой величины определите соответствующий характер её изменения:
- увеличится
- уменьшится
- не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
- Записать формулы для каждой из величин.
- Определить, как зависит эта физическая величина от начальной скорости.
- Определить характер изменения физической величины при уменьшении начальной скорости.
Решение
Время полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, время никак не зависит от начальной скорости. Поэтому оно при уменьшении начальной скорости вдвое не изменится.
Дальность полета тела, брошенного горизонтально, определяется формулой:
Исходя из формулы, дальность полета зависит от начальной скорости прямо пропорционально. Поэтому, если начальная скорость тела будет уменьшена вдвое, дальность полета тоже уменьшится (вдвое).
Ускорение свободного падения — величина постоянная для нашей планеты. Поэтому изменение начальной скорости никак не повлияет на него. Ускорение не изменится.
Значит, верный ответ — 323.
Ответ: 323
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 18.3k
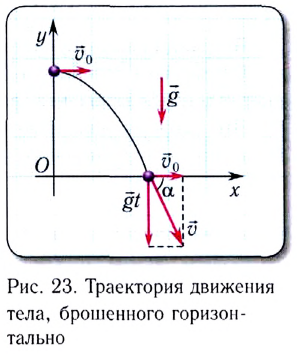
Движение горизонтально брошенного тела:
Рассмотрим движение шара, движущегося прямолинейно по поверхности стола с высотой
При достаточно малом сопротивлении воздуха, которым можно пренебречь, тело будет двигаться в горизонтальном направлении равномерно со скоростью 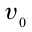
в горизонтальном направлении в любой момент времени 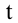
Проекции скорости тела на оси 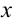
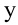
В вертикальном же направлении, двигаясь равноускоренно без начальной скорости, тело будет свободно падать с высоты 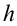
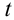
Из соотношений (1.21) и (1.22) уравнение траектории движения горизонтально брошенного тела на плоскости 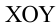
Выражение (1.24) является уравнением параболы. Значит, горизонтально брошенное тело будет двигаться по параболической линии. Время полета тела, брошенного горизонтально с высоты 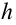
В этом случае формула для расчета длины полета тела будет иметь вид:
Горизонтально брошенное тело, одновременно двигаясь в горизонтальном направлении равномерно и в вертикальном направлении равноускоренно, свободно падает. К концу движения (после истечения времени 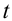
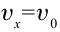
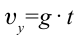
или
Перемещение и траектория тела при криволинейном движении неравны между собой. Модуль вектора и направление движения горизонтально брошенного тела на протяжении движения меняются непрерывно.
Образец решения задачи:
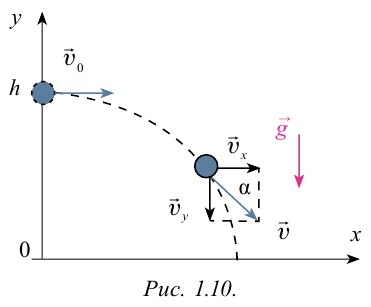
Тело брошено горизонтально на высоте 35 м со скоростью 30м/с. Найти скорость тела при падении на землю.
Дано:
Найти:
Формула:
Решение:
Ответ: 40 м/c.
Движение тела, брошенного горизонтально и под углом к горизонту
Если материальная точка участвует одновременно в нескольких движениях, то такое движение называют сложным.
Примером сложного движения является движение под действием силы тяжести в том случае, если падающему телу сообщена начальная скорость, непараллельная вектору ускорения свободного падения.
Рассмотрим движение тела, брошенного горизонтально со скоростью 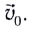
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного с постоянной скоростью 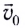
Движение тела в горизонтальном направлении будет описываться уравнением
а в вертикальном — уравнением
Здесь 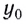
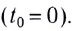
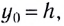
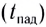
условия
Для получения уравнения траектории движения у(х) необходимо исключить время из уравнений движения (1) и (2). Из уравнения (1) выражаем время t и подставляем в уравнение (2). Получаем
Это уравнение параболы, ветви которой направлены вниз, так как коэффициент перед множителем 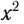
Скорость вдоль направления оси Ох остается неизменной и равной
Вдоль оси Оу движение равноускоренное. В начальный момент времени вертикальная составляющая скорости равна нулю 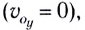
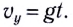
Угол между начальной скоростью 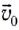
В приведенных формулах сопротивление воздуха не учитывается.
Рассмотрим теперь движение тела, брошенного со скоростью 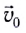
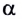
Это сложное движение можно представить в виде суммы двух независимых движений — равномерного в горизонтальном направлении со скоростью
и равноускоренного в вертикальном направлении с ускорением 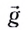
скоростью
В том случае, если система координат выбрана так, что начальные координаты 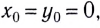
Как и при движении тела, брошенного горизонтально, траектория представляет собой параболу, ветви которой направлены вниз, поскольку коэффициент перед 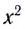
где l — дальность полета тела, 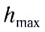
Модули горизонтальной 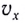
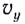
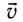
Мгновенную скорость 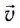
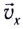
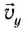
Время подъема тела можно найти из условия
Если сопротивление воздуха при движении не учитывается, то время подъема равно времени падения: 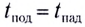
Таким образом, время полета тела можно найти как
Определив вертикальную составляющую скорости 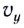
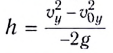
Максимальная высота подъема тела 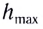
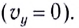
Дальность полета l — расстояние, пройденное телом за время полета 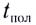
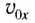
Таким образом, дальность полета определяется модулем начальной скорости 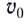
Заметим, что согласно формуле (9) при неизменном модуле начальной скорости тела максимальная дальность 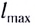
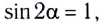
- Движение тела, брошенного под углом к горизонту
- Принцип относительности Галилея
- Движение в гравитационном поле
- Зависимость веса тела от вида движения
- Вертикальное движение тел в физик
- Неравномерное движение по окружности
- Равномерное движение по окружности
- Взаимная передача вращательного и поступательного движения
- Это движение в плоскости, поэтому для описания движения необходимо 2 координаты.
- Считаем, что движение происходит вблизи поверхности Земли, поэтому ускорение тела – ускорение свободного падения (a = g).
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли (g) – вдоль вертикальной оси (y), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
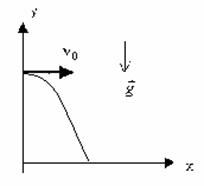
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
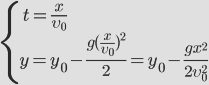
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Решим задачу для случая х0=0 и y0=0.
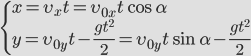
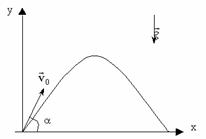
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
.
Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.
Время полета:


Зная время полета, найдем максимальное расстояние, которое пролетит тело:
Дальность полета:
Из этой формулы следует, что:
— максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 450;
— на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории.
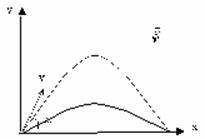
Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело.
Время, за которое тело долетит до середины, равно: 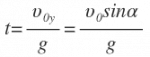
Время подъема:
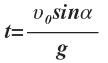
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
I. Механика
Тестирование онлайн
Движение тела, брошенного горизонтально
Рассмотрим движение тела, брошенного в горизонтальном направлении с некоторой высоты h и начальной скоростью v0. Траектория такого движения имеет вид спадающей ветви параболы.
Для описания движения тела необходимо задать координатные оси. Ось Оy направим вертикально вверх, горизонтальную ось Оx — вдоль полета. Такое движение по криволинейной траектории рассматривают как сумму двух движений, протекающих независимо друг от друга — движение с ускорением свободного падения вдоль оси Оy и равномерного прямолинейного движения вдоль оси Оx.
Движение вдоль горизонтальной оси Оx равномерное.
Движение вдоль вертикальной оси ОУ — свободное падение тела с некоторой высоты h (на графике y0).
Реальная скорость тела в некоторый момент времени — это векторная сумма горизонтальной составляющей скорости vx и вертикальной скорости vy.

Движение тела, брошенного под углом к горизонту
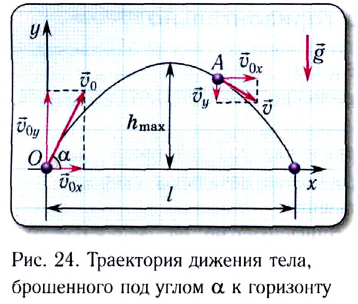
Угол броска определяет траекторию движения, дальность полета, максимальную высоту подъема тела.
Аналогично движению тела, брошенного горизонтально, это движение рассматривают как сумму независимых движений: равномерного движения вдоль горизонтальной оси ОХ и свободного падения тела вдоль вертикальной оси ОУ.
Движение вдоль горизонтальной оси ОХ равномерное.
Движение вдоль вертикальной оси ОУ — свободное падение тела, брошенного вертикально вверх с некоторой начальной скоростью v0y. Тело поднимается на максимальную высоту h, затем возвращается вниз.
Действительная скорость, с которой движется тело.
Упражнения
При каком угле бросания достигается максимальная дальность полета?
Движение тела, брошенного горизонтально или под углом к горизонту.
Так как мы пренебрегаем сопротивлением воздуха, то ускорение направлено только к поверхности Земли ( g ) – вдоль вертикальной оси ( y ), вдоль оси х движение равномерное и прямолинейное.
Движение тела, брошенного горизонтально.
Выразим проекции скорости и координаты через модули векторов.
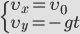
Для того чтобы получить уравнение траектории, выразим время tиз уравнения координаты x и подставим в уравнение для y:
Движение тела, брошенного под углом к горизонту.
Порядок решения задачи аналогичен предыдущей.
Докажем, что траекторией движения и в этом случае будет парабола. Для этого выразим координату Y через X (получим уравнение траектории):
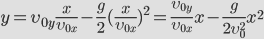
Мы получили квадратичную зависимость между координатами. Значит траектория — парабола.
Найдем время полета тела от начальной точки до точки падения. В точке падения координата по вертикальной оси у=0.

Используя то, что парабола – это симметричная кривая, найдем максимальную высоту, которой может достичь тело .
Время, за которое тело долетит до середины, равно: 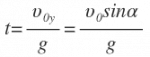
Тогда:
Максимальная высота:
Скорость тела в любой момент времени направлена по касательной к траектории движения (параболе) и равна
Угол, под которым направлен вектор скорости в любой момент времени:
Баллистическое движение — характеристика, основные формулы и уравнения
Как упадет брошенный предмет, по какой траектории полетит пуля и как рассчитать правильное направление для попадания в цель – всё это объясняется таким понятием как баллистическое движение и изучается соответствующей наукой.
Наверное каждый при просмотре фильмов о работе экспертов-криминалистов слышал выражение «аэробаллистическая экспертиза», и удивлялся тому, как лихо они определяют местоположение стрелка, и тип, а иногда и модель оружия, из которого был произведен, зачастую, фатальный выстрел.
Понятие баллистики
Определение баллистики звучит следующим образом – наука о движении тел, двигающихся в пространстве. Она изучает в первую очередь принципы движения всевозможных объектов, в частности пуль и снарядов, а также законы природы, влияющие на это движение и способность тела преодолевать возникшие на его пути преграды.
Физика и математика — вот основы, на которых базируется эта наука, они позволяют при должных знаниях рассчитывать траекторию полёта пули, исходя из воздействия на неё внешних сил, и её проникающую способность.
Сама же наука о законах полета снарядов делится на 4 направления:
Исследование движения пули или снаряда в канале ствола орудия изучает направление, которое называется внутренняя баллистика.
Поведение снаряда на выходе из канала ствола и в районе дульного среза исследуется промежуточной баллистикой и используется в разработке пламегасящих устройств и глушителей.
Вопросы движения снаряда в атмосфере и при воздействии внешних факторов изучаются внешней баллистикой. Основная область её применения – установление поправок на упреждение и влияние скорости ветра на траекторию.
Изучение проникающей способности снаряда – цель исследований баллистики под названием преградная (терминальная), которую изучают специалисты по вопросам бронезащиты.
История возникновения баллистики
Испокон веков основным занятием человека являлось уничтожение себе подобных. Сперва для этого использовались булыжники и палки, после чего человечество пришло к тому, что дистанционное оружие дает целый ряд преимуществ его владельцу.
Так или иначе баллистика изучалась по мере развития человечества, параллельно с развитием механизмов для поражения противника на расстоянии.
Метательные камни, ножи и дротики, ручные пращи, луки, арбалеты, а впоследствии – баллисты, катапульты, требушеты, толлеоны и, в конце концов, огнестрельное оружие и артиллерийские орудия — все эти средства толкали науку баллистики на протяжении всей своей истории.
Начало изучения траектории полета снаряда, как науки, было положено Николло Тарталья в 1537 году, начавшим исследование кривой движения этого тела. Продолжил изучение Галилей, сформулировав параболическую теорию.
Развивал данную тему и Ньютон, благодаря изучению законов воздушного сопротивления которого стало возможным доказать невозможность параболической кривой полета снаряда. Его дело продолжил Бенджамин Робинс, основное исследование которого — расчет начальной скорости ядра.
Он даже изобрел актуальный по сей день баллистический маятник. Прибор, с помощью которого определяют эффективность взрывчатых веществ, фиксируя при их подрыве угол отклонения маятника.
Далее баллистика развивалась семимильными шагами. Вошедшее в обиход в начале XIX века нарезное оружие, а также использование адаптированных под него снарядов и нового образца патрона, с пулей продолговатой формы, а точнее – необходимость изучения их эффективности и дальнейшей оптимизации, стали серьезным толчком в изучении данной науки, поскольку характеристики нового оружия были весьма высоки, что обуславливало широкую его популярность, и как следствие – высокий спрос.
Одним из ключевых витков истории баллистики стала разработка численного метода интегрирования дифференциальных уравнений, созданного Карлом Рунге и Мартином Кутта. Определенные элементы их метода позволяли с максимальной точностью вести расчеты траектории тел в пространстве.
Появлялись всё новые виды вооружения, конструкторы отчаянно экспериментировали с длиной ствола, внутренними нарезами и наполнением патрона, двигая науку вперед.
Баллистическая траектория
Итак, что же в итоге представляет собой баллистическая траектория? Современная энциклопедия гласит: «Это траектория движения свободно брошенного тела под действием только силы тяжести».
Например, межконтинентальные баллистические ракеты считаются таковыми, поскольку продолжают своё движение к цели после выключения двигателей, как раз-таки по траектории, которую называют баллистической.
Здесь же – расчет ведения огня по настильной траектории, проще говоря – плавно опускающейся линии по ходу полета снаряда, и расчет возможности преодолевать возвышения по пути к конечной точке.
Фактически, таковым является движение любого тела в пространстве, при отсутствии какой-либо дополнительной тяги.
Основные формулы баллистического движения
При расчетах и изучении баллистического движения любого тела, стоит обратить внимание на огромное количество факторов – массу, скорость и обтекаемость тела, атмосферные условия и многое-многое другое. Но даже при учете этого, в баллистике есть свои основные формулы, применяемые в исследованиях.
На брошенное под углом к горизонту тело в полете действует по меньшей мере – сила тяжести и сопротивление воздуха. Если исключить из этого силу сопротивления, то, согласно 2-го закону Ньютона, тело движется с ускорением, равным ускорению свободного падения; проекции ускорения на координатные оси равны ах = 0, ау = -g.
Проекции скорости тела, следовательно, изменяются со временем следующим образом:
Vx = Vx0 = V0 * cos α;
Vy = Vy0 – g * t = V0
* sin α – g * t,
где V0 — начальная скорость, α – угол бросания.
Координаты тела, следовательно, изменяются так:
x = x0 + V0 * t * cos α;
y = y0 + V0 * t * sin α – 0,5 * g * t 2 .
Если за точку отсчета берутся координаты х = у = 0, то:
x = V0 * t * cos α;
y = V0 * t * sin α – 0,5 * g * t 2 .
Дальнейшие расчеты производятся при введении таких переменных как дальность полета и время, в итоге же получается финальное уравнение траектории движения. Выглядит оно следующим образом:
y = x * tg α – g * x 2 / 2 * V0 2 * cos 2 α.
Вычисляем баллистические траектории в играх
При разработке видеоигр часто встречается задача вычисления угла выстрела для попадания в цель. Она настолько распространена, что я писал код для её решения в буквальном смысле для каждой игры, над которой работал.
Когда возникала эта проблема, я обычно брал ручку с блокнотом и решал её с нуля. Мне это надоело. Чтобы сэкономить себе из будущего немного времени, я выложу это решение в Интернет. Кроме того, я расскажу о необычной «фишке», которую предпочитаю использовать из соображений эстетики.
Уравнения движения
Задача всегда начинается одинаково. У нас есть стреляющий и цель: под каким углом нужно стрелять снарядом, чтобы он поразил цель?
Существует четыре основных уравнения движения. В статье мы воспользуемся только одним.
Если объяснять на словах, то конечная позиция РАВНА исходной позиции ПЛЮС скорость, умноженная на время ПЛЮС половина ускорения, умноженная на время в квадрате. Это простое уравнение, для его решения необходимо немного алгебры и несколько тригонометрических тождеств.
Освежим знания
Прежде чем начать, давайте вкратце освежим память.
Если дан снаряд с постоянной скоростью S и углом выстрела θ (theta), то мы можем вычислить компоненты скорости x и y. Или если есть S и мы каким-то образом найдём y, то можем вычислить θ и x.
Мы используем алгебру.
Мы часто будем пользоваться формулой корней квадратного уравнения.
Дальность
При разработке видеоигр нам, вероятно, нужно будет знать максимальную дальность полёта снаряда. Искусственный интеллект должен понимать, насколько близко нужно подойти, а игрокам нужны чёткие наглядные индикаторы опасных зон.
Существует очень простое уравнение максимальной дальности на плоской поверхности. Мы сразу же ринемся в омут с головой и начнём с обобщённого вида.
Если дан снаряд с постоянной скоростью (S) и гравитацией (G), то какой будет его максимальная дальность полёта?
Для тестирования и визуализации я создал демо на Unity. В нём используются чайники, стреляющие чайниками. Пиф-паф!
В демо есть несколько ползунков. В видео показан индикатор дальности стрельбы нашего чайника-турели. При увеличении скорости увеличивается дальность. При снижении гравитации дальность тоже растёт. Всё довольно просто.
Угол стрельбы для попадания по неподвижной мишени
Теперь начинается интересное.
Если снаряд имеет постоянную скорость (S), а гравитация равна (G), то под каким углом его нужно выстреливать, чтобы попасть в неподвижную мишень?
Бах. Теперь у нас есть два уравнения и два неизвестных. Давайте их проанализируем.
- Первое уравнение, два неизвестных (t, θ)
- Второе уравнение, два неизвестных (t, θ)
- Вычислить t из (1)
- Подставить (3) в (2)
- Тригонометрическая подстановка: sin θ/cosθ = tanθ
- Тригонометрическая подстановка: 1/(cos θ)^2 = 1 + (tan θ)^2
- Развернём и преобразуем
- Формула корней квадратного уравнения
- Умножим верхнюю/нижнюю часть на -S^2/x. Перенесём S^4/x^2 под корень
- Применим к каждой части арктангенс
Та-да! В результате мы получили два угла. Один высокий и один низкий. Вот как это выглядит на практике.
Визуальное несовершенство
Взгляните на показанный выше gif. Когда чайник начинает стрелять, всё выглядит довольно неплохо. Высокая дуга красива и радует глаз. Низкая дуга кажется чёткой и эффективной.
Однако при увеличении дальности всё становится не таким красивым. Низкая дуга почти плоская. Высокая дуга чрезмерно высока. В этом и заключается проблема снаряда с постоянной скоростью. Он выглядит красиво, только когда цель находится на границах его радиуса дальности.
Существует ли способ получше?
Скорость горизонтального перемещения
Я часто предпочитаю задавать горизонтальную скорость снаряда, только в плоскости земли. Тогда я могу явным образом задать высоту дуги. То есть переменной становится скорость и гравитация.
Такой подход имеет множество преимуществ. Во-первых, он всегда выглядит красиво!
Во-вторых, его дизайн более интуитивен. Дизайнеров не волнует абсолютная скорость. Им важно, что турель имеет дальность 20 метров и что для перемещения на это расстояние снарядам требуется 1 секунда. Они не обязаны пользоваться строящим графики калькулятором, чтобы менять значения баланса. А художественные изменения не должны влиять на геймплейные механики.
В-третьих, так проще попадать по движущейся мишени. Чуть позже я раскрою это подробнее.
Вот как это выглядит:
Вычисление скорости горизонтального перемещения
Если дан снаряд с горизонтальной скоростью (S) и пиковой высотой (y_peak), то какими должны быть скорость и гравитация для поражения неподвижной мишени?
- Основное уравнение движения
- Решаем (1), подставив 2
- Зададим, что y_peak (пользовательская константа) снаряд достигает во время (1/2)t
- Зададим, что y_end (высота цели) снаряд достигает во время t
- Магия!
- Ещё магия!
- Вектор стрельбы равен (S, v.y) с гравитационным ускорением g
Вуаля! Хотя постойте-ка. Магия? Это жульничество! Да, но вполне оправданное.
Пункты (3) и (4) — это ещё два уравнения с двумя неизвестными. Я ленивый и не хочу их записывать. Плюс я запутаюсь и перепутаю знак, поэтому позволю компьютеру решить их за меня.
Точнее, я воспользовался Wolfram Alpha. Рекомендую каждому иметь Wolfram в своём инструментарии, он довольно полезен.
Если a+c == 2b , то y0 , y_peak и y_end лежат на одной прямой. То есть мы стреляем по прямой.
Скорость горизонтального перемещения при подвижной мишени
Итак, у нас есть два разных вычисления траектории. Однако враги обычно не стоят на месте, они перемещаются. Нам нужно вычислять траекторию, чтобы поражать подвижную мишень.
Именно здесь проявляются все достоинства скорости горизонтального перемещения. Задав скорость в плоскости земли, очень просто выполнить вычисления для подвижной мишени.
- Где X — позиция мишени, а V — её скорость
- Возводим обе части в квадрат.
- Преобразуем в квадратное уравнение
- Применяем формулу корней квадратного уравнения
Пункты с 5 по 9 см. в предыдущем разделе.
Меня это очень радует. Пиу-пиу-пиу!
Постоянная скорость с подвижной мишенью
А что если нам нужно поразить подвижную мишень снарядом с постоянной скоростью? Ой-ёй. Это очень запутанная задача! Даже не знаю, как к ней подступиться.
За всю мою карьеру мне не доводилось её решать. Обычно в играх не нужна точная артиллерия. Это просто неинтересно! Вместо этого мы приблизительно вычисляем будущую позицию и целимся в случайную точку рядом с ней. Игроки воспринимают артиллерийский огонь как дождь из глупых снарядов, а не как гарантированную смерть с лазерным наведением.
В процессе написания этого поста я нашёл решение задачи снаряда с постоянной скоростью и движущейся мишени, которого не было в Интернете в готовом виде. Стоит заметить, что вам, вероятно, не понадобится реализовывать его в своей игре. Но я потратил на него много времени, поэтому не хочу, чтобы оно было потеряно впустую!
Уравнения четвёртой степени
Скорее всего, вы не захотите использовать его в своей игре именно из-за уравнений четвёртой степени. По сути, для решения требуется одно из таких уравнений.
Квадратные уравнения имеют простое и изящное решение в виде формулы корней квадратного уравнения. Кубические уравнения решаемы несколькими разными способами. Однако уравнения четвёртой степени — это настоящая головная боль.
Решение таких уравнений находится далеко за рамками этой статьи. Честно говоря, и за пределами моих математических способностей. К счастью для нас, в книге 1990 года Graphics Gems I есть код для решения уравнений четвёртого порядка. Я использовал этот код для своего демо. Не могу гарантировать его точности и численной устойчивости, используйте его крайне осмотрительно.
Способ первый
Итак, давайте его решим. Каким должен быть угол выстрела снарядом с постоянной скоростью по движущейся мишени? Этот способ взят из поста 2007 года Джеймса Макнейлла и дополнен информацией Райана Джакетта.
- Где P — позиция мишени, а V — скорость мишени
- Возводим обе части в квадрат
- Преобразуем
- Вычисляем коэффициенты уравнения четвёртого порядка и вставляем в SolveQuartic
- Используем t для вычисления позиции мишени при вычислении траектории до неподвижной точки.
Способ работает. Все сложные задачи выполняет SolveQuartic. Затем мы используем решение для неподвижной мишени, изложенное выше.
Способ второй
Прежде чем я нашёл первый способ, я вывел решение другим способом. Оно состоит из гораздо большего количества шагов. Однако я нахожу конечный результат более изящным. Плюс я потратил примерно восемь листов бумаги и не хочу, чтобы эти деревья пожертвовали собой зазря.
Чёрт возьми. 32 шага!? Это хуже, чем кажется.
1–7 — объявляем переменные.
8–11 — объявляем систему уравнений. Четыре уравнения, четыре неизвестных — d, e, f, t.
12–15 — вычисляем по (8) величину d. Перемножаем d^2 на будущее.
16–19 — вычисляем по (10) величину f. Перемножаем f^2 на будущее.
20–24 — вычисляем по (9) величину e. Перемножаем e^2 на будущее.
25–27 — вычисляем по (11) величину e^2. Подставляем d^2 и f^2.
28–30 — приравниваем (27) к (24). Умножаем на t^2 и преобразуем в уравнение четвёртой степени.
31 — подставляем коэффициенты в SolveQuartic.
32 — подставляем положительные вещественные корни в (14), (18), (23) для d, e, f.
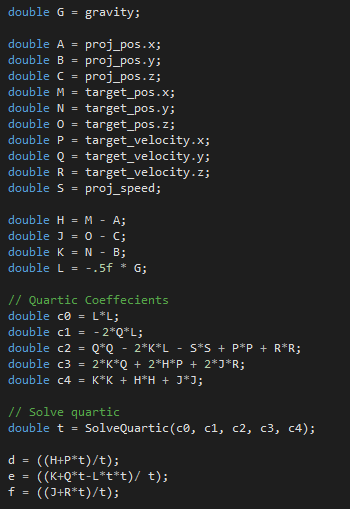
Код довольно короткий. Объявлению переменных отведено больше строк, чем самим вычислениям! Разумеется, кроме SolveQuartic.
Предупреждение
Код, написанный для этого теста, не проверен в бою, а пост никем не рецензировался. Вероятно, в нём есть несколько опечаток, ошибок и неучтённых пограничных случаев. Если найдёте подобные ошибки, пожалуйста, сообщите мне. Втайне, чтобы никто не узнал о моём позоре.
Рассматривайте этот код не как готовое решение, а как опорную точку.
Инструменты
При создании этого поста я использовал несколько инструментов. Многие из них были для меня новыми.
- Unity для создания демо.
- Paper, Affinity Designer и MSPaint для создания изображений.
- Arachnid Latex + MathJax для формул LaTeX.
- FFmpeg для преобразования последовательности скриншотов в анимацию.
- Gfycat для встраивания анимаций.
- Чайник из Юты. Пиу-пиу!
Синтаксис LaTeX ужасен, его сложно учить. Все формулы LaTeX можно найти здесь. Вот пример:
Заключение
Вот и всё. Я потратил на этот пост гораздо больше времени, чем ожидал. Я решил задачу, которую никогда не решал прежде и изучил несколько новых инструментов. И это того стоило.
В этом посте нет ничего нового или оригинального. Я пытался объяснять подробно, но чтобы не быть при этом слишком многословным. Мне очень нравится, что теперь полные описания можно найти в одном месте. Надеюсь, они окажутся полезными для людей.
http://sprint-olympic.ru/uroki/fizika/97147-ballisticheskoe-dvijenie-harakteristika-osnovnye-formyly-i-yravneniia.html
http://habr.com/ru/post/538952/
| Движение тела, брошенного горизонтально или под углом к горизонту. | |
|
|
 |
|
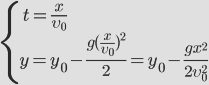 |
— между координатами квадратичная зависимость, траектория – парабола! |
 |
|
| Следовательно, для решения этой задачи необходимо решить уравнение
|
|
| Оно будет иметь решение при t=0 (начало движения) и |  |
|
Зная время полета, найдем максимальное расстояние, которое пролетит тело: Дальность полета: Из этой формулы следует, что: — максимальная дальность полета будет наблюдаться при бросании тела (при стрельбе, например) под углом 45 0 ; — на одно и то же расстояние можно бросить тело (с одинаковой начальной скоростью) двумя способами – т.н. навесная и настильная баллистические траектории. |
 |