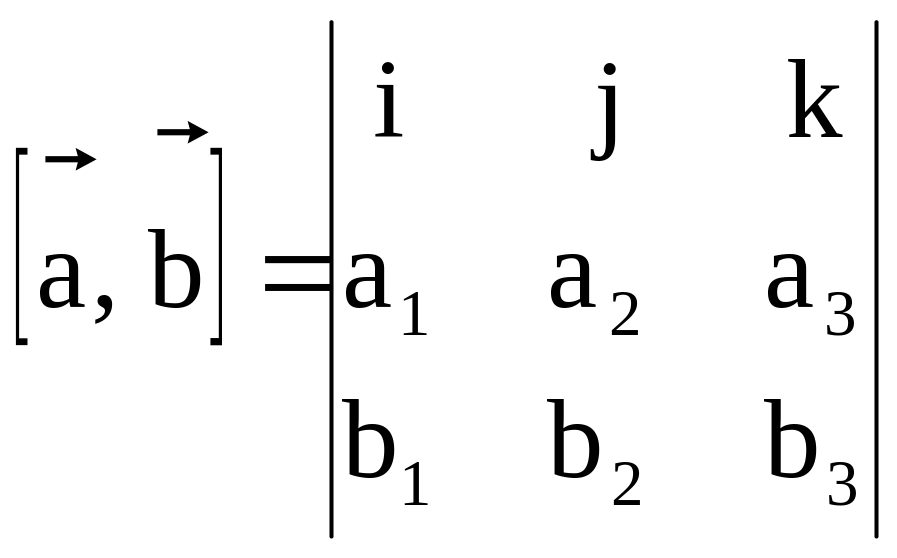Онлайн калькулятор. Вычисление угла между векторами
Этот онлайн калькулятор позволит вам очень просто найти угол между двумя векторами (косинус угла между векторами) для плоских и пространственных задач.
Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление угла между векторами и закрепить пройденный материал.
Калькулятор для вычисления угла между векторами
Инструкция использования калькулятора для вычисления угла между векторами
Ввод даных в калькулятор для вычисления угла между векторами
В онлайн калькулятор можно вводить числа или дроби. Более подробно читайте в правилах ввода чисел.
Дополнительные возможности калькулятора для вычисления угла между векторами
- Между полями для ввода можно перемещаться нажимая клавиши «влево» и «вправо» на клавиатуре.
Теория. Вычисление угла между векторами
Угол между двумя векторами a и b можно найти использовав следующую формулу:
Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Задача 32394 1. На векторах a = (9,1,1) и b = (1,1,9).
Условие
1. На векторах a = (9,1,1) и b = (1,1,9) построен параллелограмм.
Найти:
а) угол между диагоналями параллелограмма;
в) высоту параллелограмма, опущенную на вектор b.
Решение
По правилу сложения и вычитания векторов, одна диагональ является суммой векторов, вторая разностью.
vector=vector+vector=(10;2;10)
vector=vector-vector=(8;0;-8)
vector*vector=10*8+2*0+10*(-8)=0
Скалярное произведение равно 0, значит диагонали параллелограмма взаимно перпендикулярны, угол между диагоналями 90^(o)
С другой стороны
S=b*h
|vector|=sqrt(1^2+1^2+9^2)=sqrt(83)
h=8sqrt(102)/sqrt(83)
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
- Векторная алгебра.
- Высшая математика.
- Векторная алгебра.
- Скалярное произведение векторов, свойства. Длина вектора. Угол между векторами.
Скалярное произведение векторов, свойства. Длина векторов. Угол между векторами.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Длина вектора.
Пусть вектор $overline a=(x, y, z)$ представлен своими координатами в прямоугольном базисе. Тогда его длину можно вычислить по формуле $$|overline a|=sqrt.$$
Скалярное произведение векторов.
Если заданы координаты точек $A(x_1, y_1, z_1) $ и $B(x_2, y_2, z_2),$ то координаты вектора $overline$ можно найти по формулам $$overline=(x_2-x_1, y_2-y_1, z_2-z_1).$$ Скалярным произведением ненулевых векторов $a_1$ и $a_2$ называется число $$(a_1, a_2)=|a_1||a_2|cos(widehat).$$
Для скалярного произведения наряду с обозначением $(a_1,a_2)$ используется также обозначение $a_1a_2.$
Геометрические свойства скалярного произведения:
1) $a_1perp a_2Leftrightarrow a_1a_2=0$ (условие перпендикулярности векторов).
2) Если $varphi=(widehat),$ то $$0leqvarphi 0; qquadqquad frac <pi>
Алгебраические свойства скалярного произведения:
2) $(lambda a_1)a_2=lambda (a_1 a_2);$
Если векторы $a_1(X_1, Y_1, Z_1)$ и $a_2(X_2, Y_2, Z_2)$ представлены своими координатами в прямоугольном базисе, то скалярное произведение равно $$a_1a_2=X_1X_2+Y_1Y_2+Z_1Z_2. $$
Из этой формулы, в частности, следует формула для определения косинуса угла между векторами:
Решение.
а) $$a_1^2=(a_1, a_1)=|a_1||a_1|cos(widehat)=|a_1|^2=3^2=9.$$
б) $(3a_1-2a_2)(a_1+2a_2);$
Поскольку скалярное произведение зависит от длин векторов и угла между ними, то заданные векторы можно выбрать произвольно учитывая эти характеристики. Пусть $a_1=(3; 0). $ Тогда вектор $a_2,$ имея длину $|a_2|=4,$ и, образуя угол $frac<2pi><3>$ с положительной полуосью оси $OX,$ имеет координаты $x=|a_2|cosfrac<2pi><3>=-frac<4><2>=-2; $
$3a_1-2a_2=3(3;0)-2(-2;2sqrt 3)=(9;0)-(-4; 4sqrt 3)=(13;-4sqrt 3);$
$a_1+2a_2=(3; 0)+2(-2;2sqrt 3) = (3; 0)+ (-4; 4sqrt 3)= (-1; 4sqrt 3).$
$(3a_1-2a_2)(a_1+2a_2)=(13; -4sqrt 3)(-1; 4sqrt 3) =-13-48=-61.$
в) $(a_1+a_2)^2.$
$a_1+a_2$=$(3; 0)+(-2; 2sqrt 3)=(1; 2sqrt 3).$
$(a_1+a_2)^2=(1; 2sqrt3) (1; 2sqrt 3)=1+12=13.$
Ответ: a) 9; б) -61; в) 13.
2.67. Вычислить длину диагоналей параллелограмма, построенного на векторах $a=p-3q, $ $b=5p+2q,$ если известно, что $|p|=2sqrt<2>, |q|=3, (widehat)=frac<pi><4>.$
Решение.
Способ 1.
Из треугольника $ABC$ имеем $AC=AB+BC=a+b=p-3q+5p+2q=6p-q.$
Зная длину векторов $p$ b $q$ и угол между этими векторами, можно найти длину вектора $AC$ по теореме косинусов:
Из треугольника $ABD$ имеем: $BD=AD-AB=b-a=5p+2q-p+3q=4p+5q.$
По теореме косинусов находим длину вектора $BD:$
$|BD|^2=|4p|^2+|5q|^2-8p5qcos widehat<(6p, q)>=$ $128+225+240=593.$
Пусть $q=(3; 0). $ Тогда вектор $p,$ имея длину $|p|=2sqrt 2,$ и образуя угол $frac<pi><4>$ с положительной полуосью оси $OX$ имеет координаты
Из треугольника $ABC$ имеем
Из треугольника $ABD$ имеем
$BD=AD-AB=b-a=5p+2q-p+3q=4p+5q=$ $=4(2; 2)+5(3;0)=(8; 8)+(15; 0)=(23; 8).$
Ответ: $15, sqrt <593>.$
2.68. Определить угол между векторами $a$ и $b$ если известно, что $(a-b)^2+(a+2b)^2=20$ и $|a|=1, |b|=2.$
Ответ: $2pi/3$
$|a_1|=3; |a_2|=5. $ Определить, при каком значении $alpha$ векторы $a_1+alpha a_2$ и $a_1-alpha a_2$ будут перпендикулярны.
Ответ: $alpha=pmfrac<3><5>$
В треугольнике $ABC$ $overline=3e_1-4e_2;$ $overline=e_1+5e_2.$ Вычислить длину его высоты $overline,$ если известно, что $e_1$ и $e_2$ взаимно перпендикулярные орты.
http://reshimvse.com/zadacha.php?id=32394
http://mathportal.net/index.php/vektornaya-algebra/122-skalyarnoe-proizvedenie-vektorov-svojstva-evk
Примеры решения задач
Задача 1.
Определить длины диагоналей параллелограмма,
построенного на векторах
и
,
где
таковы, что
.
Решение.
Диагонали параллелограмма есть векторы
и
.
Вычислим длину вектора
:
.
Аналогично
вычисляется длина вектора
.
Задача 2.
Найдите вектор
,
коллинеарный вектору
и удовлетворяющий условию
.
Решение.
Обозначим вектор
,
тогда из условий задачи
или
,
тогда
.
Итак:
.
Задача 3.
Найти проекцию вектора
на направление вектора
.
Решение.
.
По формуле проекции вектора на ось будет
иметь место равенство
.
Задача 4.
Даны векторы:
.
П
роверить,
есть ли среди них коллинеарные. Найти
.
Решение.
Условие коллинеарности имеет вид
.
Этому условию удовлетворяют векторы
.
Следовательно, они коллинеарны. Найдем
длины
векторов
:
.
Угол между векторами
определяется по формуле
.
Т
огда
,
.
Используя формулу
,
получим
.
Задача 5.
На материальную точку действуют силы
.
Найти работу равнодействующей этих сил
при перемещении точки из положения
в положение
.
Решение.
Найдем силу
и вектор перемещения
.
,
тогда искомая работа
.
Задачи
1. Векторы
взаимно перпендикулярны, а вектор
образует с ними углы
.
Зная, что
,
найти: 1)
;
2)
.
2. Вычислить длину
диагоналей параллелограмма, построенного
на векторах
,
если известно, что
.
3. Доказать, что
вектор
перпендикулярен к вектору
.
4. Зная, что
,
определить, при каком значении коэффициента
векторы
окажутся перпендикулярными.
5. Даны вершины
четырехугольника:
.
Доказать, что его диагонали взаимно
перпендикулярны.
6. Найти острый
угол между диагоналями параллелограмма,
построенного на векторах
.
7. Даны силы
.
Найти работу их равнодействующей при
перемещении точки из начала координат
в точку
.
8. Даны вершины
треугольника:
.
Найти проекцию вектора
на вектор
.
9. Найти вектор
,
перпендикулярный векторам
,
если известно, что его проекция на вектор
равна единице.
10. Сила, определяемая
вектором
,
разложена по трем направлениям, одно
из которых задано вектором
.
Найти составляющую силы
в направлении вектора
.
11. Даны вершины
треугольника:
.
Найти его внутренний угол при вершине
А и внешний угол при вершине В.
12. Даны три
последовательные вершины параллелограмма:
.
Найти его четвертую вершину D
и угол между векторами
.
13. На оси
найти точку, равноудаленную от точек
.
14. Доказать, что
треугольник с вершинами
прямоугольный.
Домашнее задание
1. Вычислить
скалярное произведение двух векторов
,
зная их разложение по трем единичным
взаимно перпендикулярным векторам
;
.
2. Найти длину
вектора
,
зная, что
– взаимно перпендику-
лярные орты.
3. Векторы
попарно образуют друг с другом углы,
каждый из которых равен
.
Зная, что
,
определить модуль вектора
.
4. Доказать, что
вектор
перпендикулярен к вектору
.
5. Даны векторы
,
совпадающие со сторонами треугольника
АВС. Найти разложение вектора, приложенного
к вершине В этого треугольника и
совпадающего с его высотой BD
по базису
.
6. Вычислить угол
между векторами
,
где
—
единичные взаимно перпендикулярные
векторы.
7. Даны силы
,
приложенные к одной точке. Вычислить,
какую работу производит равнодействующая
этих сил, когда ее точка приложения,
двигаясь прямолинейно, перемещается
из положения
в положение
.
8. Даны вершины
треугольника
.
Определить его внутренний угол при
вершине В.
9. Вычислив
внутренние углы треугольника с вершинами
,
,
убедиться, что этот треугольник
равнобедренный.
10. Найти вектор
,
зная, что он перпендикулярен векторам
и
.
11. Найти вектор
,
коллинеарный вектору
и удовлетворяющий условию
,
где
.
12. Вычислить
проекцию вектора
на ось вектора
.
13. Даны векторы
.
Вычислить
.
14. Даны точки
.
Вычислить проекцию вектора
на ось вектора
.
Ответы к задачам
1) -7, 13. 2) 15,
.
4)
.
6)
.
7) 2. 
9)
.
10)
.
11)
.
12)
.
13)
.
Ответы к домашнему
заданию
1) 9. 2) 5. 3) 10. 5)
.
6)
.
7) 13. 
.
10)
.
12) 6. 13) 5. 14) 3.
Занятие 3
Векторое
произведения векторов. Смешанное
произведение векторов
Определение1.
Тройка
некомпланарных векторов
называется правой (левой) если, находясь
внутри телесного угла, образованного
приведенными к общему началу векторами
и от него к
,
човершающимся против часовой стрелки
(по часовой стрелке)
Тройка правая
Тройка левая
Определение
2. Векторным
произведением вектора
на вектор
называется вектор
,
длина и направление которого определяются
условиями:
1.
,
где
— угол между
.
2.
.
3.
— правая тройка векторов.
Свойства
векторного произведения
1.
(свойство антиперестановочности
сомножителей);
2.
(распределительное относительно суммы
векторов);
3.
(сочетательное относиельно числового
множителя);
4.
(равенство нулю векторного произведения
означает коллинеарность векторов);
5.
,
т. е. момент сил равен векторному
произведению силы на плечо.
Если вектор
,
то
.
Определение
3. Смешанным
произведением
трех векторов называется число,
определяемое следующим образом:
.
Если векторы заданы своими координатами:
,
то
~
.
Свойства
смешанного произведения
1. Необходимым и
достаточным условием компланарности
векторов
является равенство
= 0.
2. Объем
параллелепипеда, построенного на
векторах
:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Валентина |
вектор а(1;1;-1) вектор b(1;-2;3) c=a+b c(2;-1;2) a+d=b; d=b-a; d(0;-3;4) cos фи = cd/|c||d| = (0+3+8)/корень(4+1+4) корень(0+9+16) = = 11/(3*5)=11/15 S=1/2 d1*d2*sin фи = 1/2 |c||d| sin фи = = 1/2 * корень(4+1+4) корень(0+9+16) корень(1-121/225) = = 1/2 *15 корень(104) / 15 = корень(26) |