Как найти угол под которым пересекаются линии

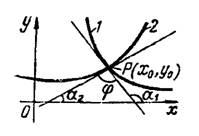
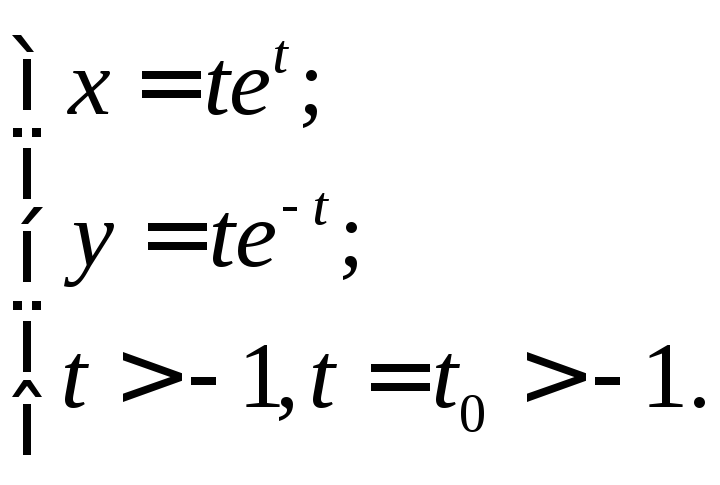Угол между двумя пересекающимися кривыми определяется как угол между двумя прямыми, касательными к кривым в точке их пересечения (рис. 1) по формуле

где и — угловые коэффициенты касательных к кривым в точке их пересечения ,
т. е. частные значения в точке производных от по из уравнений этих кривых:

Рис.1

Пример 1. Найти углы, под которыми пересекаются следующие линии:
1) прямая и парабола ;
2) эллипс и парабола ;
3) синусоида и косинусоида .
Решение.
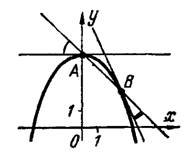
1) Совместно решая уравнения параболы и прямой, находим, что они пересекаются в двух точках: и , рис.2.

Рис.2

Далее находим производную от по из уравнения параболы: и определяем угловые коэффициенты касательных к параболе в точках и , как частные значения этой производной:

Угловой коэффициент прямой один и тот же во всех ее точках; у данной прямой он равен — 1.
Согласно формуле (2) получим

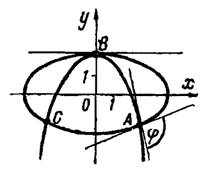
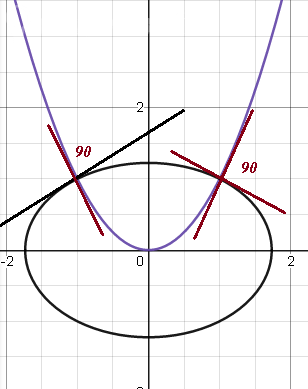
2) Решая совместно уравнения кривых, находим их общие точки: и рис.3. Затем определяем угловые коэффициенты и касательных в любой точке эллипса и параболы как производные от по из их уравнений

Рис.3

Подставляя координаты точки , получим и . Следовательно, в точке :

Под таким же углом кривые пересекаются и в точке вследствие их симметричности относительно оси .
В точке имеем: , следовательно, в точке кривые имеют общую касательную, т. е. касаются друг друга. В этой точке угол между кривыми равен нулю.
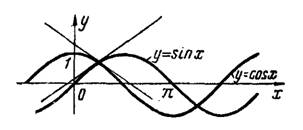
3) Абсциссы точек пересечения кривых (рис.4) определяются уравнением , решая которое, получим

Дифференцированием находим угловые коэффициенты касательных к синусоиде и косинусоиде:

Рис.4

Искомый угол между кривыми определяем по общей формуле (2)

Положительному знаку соответствует острый угол , отрицательному — тупой, смежный с ним угол .

Условие

Решение

Написать комментарий

1. Геометрический и физический смысл производной

Геометрически
производная
функциипредставляет угловой коэффициенткасательной к графику этой функции в
точке.

Если
на плоскости задана точка
и кривая как график явной функциито:

—
уравнение касательной в точке с абсциссой
,

,
— уравнение нормали в точке с абсциссой.
Если,
то уравнения касательной и нормали
имеют вид соответственно:,.

При
параметрическом задании кривой
уравнения касательной и нормали
записываются соответственно:

,
,

,

.

Угол
между кривыми
ив точке их пересечения

–
это угол между касательными к этим
кривым в точке.
Этот угол находится по формуле:.

Если
в точке
производная не определена, но функция
имеет различные односторонние пределыи,
то в этой точке графика функции существуют
две различные с соответствующими
угловыми коэффициентами,односторонние касательные, составляющие
угол, а точка называетсяугловой.

Если
,
т.е. функция имеет бесконечную производную,
то она не дифференцируема в этой точке.
В этом случае график функции имеет
вертикальную касательную (точка
перегиба).

Если
в точке
функция имеет бесконечные односторонние
производные разных знаков, то график
функции имеет две слившиеся вертикальные
касательные (асимптоты).

Если
при прямолинейном движении точки задан
закон движения
,
то скорость движения в моментесть производная пути по времени:,
ускорение в моментесть.

При
движении точки по окружности: угловая
скорость вращения
в данный момент равна производной от
угла поворотапо времени:.
Угловое ускорение точки есть первая
производная от угловой скоростиили вторая производная от угла поворота
по времени.

Сила
тока в данный момент времени равна
производной от количества протекшего
электричества по времени:
.

Химическое
истолкование производной. Пусть
— концентрация вещества, получаемого в
ходе химической реакции в момент времени.
Тогда— скорость реакции в момент.

Пример
1. В
точках пересечения эллипсов
,найти угол между ними.

Решение: Эллипсы
расположены симметрично относительно
координатных осей. Поэтому рассмотрим
только первый квадрат координатной
плоскости.

Решив
систему
найдем точку пересечения эллипсов.
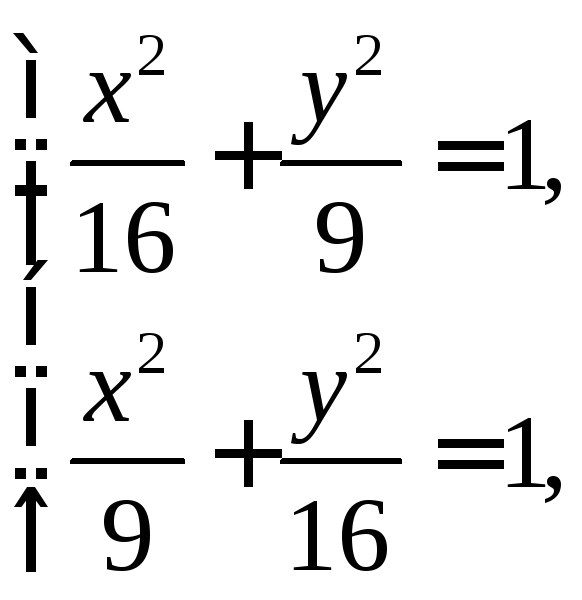
Из уравнения первого эллипса получаем,
т.е..
Следовательно.
Аналогично, для второго эллипса получим.
По формуле,получим:.

Итак,
эллипсы пересекаются в четырех точках
под углом
,
т.е. под углом, равным приблизительно.

Пример
2. Высота
снаряда, вылетевшего с начальной
скоростьюпод угломк горизонту, изменяется по закону,
где— время,— ускорение силы тяжести. В какой момент
скорость изменения высоты снаряда над
горизонтом равна нулю?

Решение:
Вычислим производную функции
.

Следовательно,
скорость изменения высоты снаряда нал
горизонтом равна нулю при
.

Найти
уравнения касательной и нормали к данной
кривой в данной точке:

1.
,.

2.
,.
Ответ:,.

3.
,.

4.
.

5.
к эллипсу
,.

6.
,.
Ответ:.

7.
;
.
Ответ:
.

8.

,

.
Ответ:
.

9.

,

.
Ответ:
.

10.

,

.
Ответ:
.

11.

,

.
Ответ:.

12.

,

.
Ответ:
.

13.

,

.
Ответ:
.

14.

Ответ:
.

15.

.
Ответ:
.

16.
Найти углы, под которыми пересекаются
линии, заданные уравнениями
и.
Ответ:,.

17.
Найти угол между кривыми:

a)
и.
Ответ:.

b)
и.
Ответ:.

Найти
углы, под которыми график функции
пересекает ось абсцисс:

18.
.

Ответ:.

19.
.
Ответ: В точкахсинусоида

пересекает
ось абсцисс под углом
.

20.
.
Ответ: В точкахугол,

в
точках
угол.

21.
.

Ответ:.

22.
.

Ответ:
в точке
угол,
в точкеугол.

23.
.

Ответ:.

24.
.
Ответ:.

25.
.

Ответ:
в точках
иугол,

в
точке
угол.

26.
.

Ответ:
в точке
угол,

в
точке
угол.

27.
Ответ:.

28.
Ответ: 0.

29.
.

Ответ:
в точке
угол,

в
точке
угол.

Найти
точки, в которых касательные к графику
функции
параллельны оси абсцисс:

30.

.
Ответ: (-1;14), (2;-13).

31.

.
Ответ: (0;-1), (1;-6), (-2;-33).

32.

.
Ответ: (-1;-58), (1;54), (7;-2106).

33.

.
Ответ:
.

34.

.
Ответ:
.

35.

.
Ответ:
.

36.

.
Ответ:
.

37.

Ответ:
.

38.

.
Ответ:
.

39.
На кривой
найти точку,
в которой касательная параллельна
прямой.
Ответ:.

40.
Найти точку линии
,
в которой касательная перпендикулярна
прямой,
составить уравнение этой касательной.
Сделать чертеж.
Ответ:.

41.
Точка движется вдоль прямой по закону
.
Найти скорость и ускорение точки в
момент времени.

Ответ:
.

42.
Угол поворота шкива в зависимости от
времени задан формулой
.
Найти угловую скорость и ускорение при.

Ответ:
угловая скорость равна
,

а
угловое ускорение не зависит от времени
и равно
.

Определить, в
каких точках и под каким углом пересекаются
кривые:

43.

,

.
Ответ:

.

44.

,

.
Ответ:

.

45.

,

.
Ответ:

.

46.

,

.
Ответ:

.

47.

,

.
Ответ:

.

48.

,

.
Ответ:

.

49.

,

.
Ответ:

.

50.

,

.
Ответ:

.

51.

и
.
Ответ:

.

52.
и
.
Ответ:

.

53.
Найти уравнение нормали к эллипсу
в точке.Ответ:
.

54.
Найти уравнение нормали к гиперболе
в точке.

Ответ:.

Найти
угол между касательной и полярным
радиусом точки касания для следующих
кривых:

55.
Спирали Архимеда
.
Ответ:.

56.
Гиперболической спирали
.
Ответ:.

57.
Логарифмической спирали
.
Ответ:.

58.
Кардиоиды
.
Ответ:.

59.
Дуги лемнискаты Бернулли
.
Ответ:.

60.
Точка движется по параболе
так, что ее абсцисса изменяется по закону(измеряется в метрах,— в секундах). Какова скорость изменения
ординаты точки через 9 с после начала
движения?
Ответ:.

61.
Радиус шара возрастает равномерно со
скоростью 5.
Какова скорость изменения объема шара
в момент, когда его радиус становится
равным 50?

Ответ: 0,05.

62.
Колесо вращается так, что угол поворота
пропорционален квадрату времени. Первый
оборот сделан за 8 с. Найти угловую
скорость через 64 с после начала движения.
Ответ:
.

63.
По оси абсцисс движутся две точки,
имеющие законы движения:
и.
С какой скоростью удаляются они друг
от друга в момент встречи (измеряется в метрах,— в секундах)? Ответ:.

64.
Паром подтягивается к берегу при помощи
каната, который наматывается на ворот
со скоростью 3.
Определить скорость движения парома в
тот момент, когда он находится в 25 м от
берега, если ворот расположен на берегу
выше поверхности воды на 4м.

Ответ:
.

65.
Под каким углом пересекаются кривые
ив точке (1;1)?
Ответ:.

66.
Определить среднюю скорость изменения
функции
на отрезке.

Ответ:.

67.
Найти расстояние от полюса до произвольной
касательной кривой
.

Ответ:.

68.
Записать в декартовых и в полярных
координатах уравнение нормали к кардиоиде
в точке с полярным углом.

Ответ:
,.

69.
Точка движется по спирали Архимеда
так, что угловая скорость вращения ее
полярного радиуса постоянна и равнав секунду. Определить скорость удлинения
полярного радиуса,
если.

Ответ:.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #

  14.02.201535.92 Mб149Сборник рецептур.djvu

• #
• #

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Длина дуги, угол между линиями, площадь области на поверхности

Краткие теоретические сведения

Зная первую квадратичную форму поверхности, мы можем решить три задачи:

2. Найти угол между двумя линиями на поверхности в точке их пересечения:
Если две линии, лежащие на поверхности с первой квадратичной формой $I_1=E,du^2+2F,du,dv+G,dv^2$, пересекаются в некоторой точке $P$ поверхности и имеют в этой точке направления $(du:dv)$ и $(delta u:delta v)$, то косинус угла между ними определяется по формуле: begin mbox,varphi = displaystylefrac<sqrtcdotsqrt> \ mbox,varphi = displaystylefrac<sqrtcdotsqrt>. end Говорим, что кривая на поверхности $vec=vec(u,v)$ в точке $(u,v)$ имеет направление $(du:dv)$, если вектор $dvec=vec_udu+vec_vdv$ является касательным вектором кривой в этой точке.

3. Найти площадь области $Omega$ на поверхности: begin S = iintlimits_sqrtdu,dv, end где $D$ — прообраз $Omega$ на плоскости $(u,v)$.

Решение задач

Задача 1 (почти Феденко 684)

Найти длину дуги кривой, заданной уравнениями $v=3u$ на поверхности с первой квадратичной формой begin I_1=du^2+frac19,mbox^2u,dv^2 end между точками $M_1(u_1,v_1)$ и $M_2(u_2,v_2)$.

Решение задачи 1

Задача 2 (почти Феденко 682)

Под каким углом пересекаются линии $$ u+v=a, ,, u-v=a,$$ лежащие на поверхности: begin x=u,mboxv, ,, y=u,mbox,v, ,, z=au. end

Решение задачи 2

Первая квадратичная форма данной поверхности: begin I_1=(1+a^2),du^2+u^2,dv^2. end

Данные линии пересекаются в точке: begin left < beginu+v&=a,\ u-v&=a. end right. quad Rightarrow quad P(u=a,v=0). end

Направления данных линий: begin du+dv=0, ,, delta u-delta v=0,, Rightarrow end begin du = -dv, ,, delta u = delta v. end

Задача 3

Дана поверхность: $$z=axy.$$ Найти углы между координатными линиями.

Решение задачи 3

Координатные линии на данной поверхности задаются уравнениями: $x=x_0$, $y=y_0$. Запишем коэффициенты первой квадратичной формы: begin &E=1+(z_x)^2=1+a^2y^2,\ &F=z_xz_y=a^2xy, \ &G=1+(z_y)^2=1+a^2x^2. end

Направления координатных линий: begin &x=x_0 ,, Rightarrow dx=0,\ &y=y_0 ,, Rightarrow delta y=0. end

Задача 4 (Дополнение к Задаче 3)

Как мы вывели в примере выше, угол между координатными линиями равен

Из формулы следует, что координатная сеть поверхности ортогональна (координатные линии пересекаются под прямым углом), тогда и только тогда, когда $F$=0.

Задача 5 (Феденко 683)

Найти периметр и внутренние углы криволинейного треугольника $$ u=pm av^2/2,,, v=1,$$ расположенного на поверхности $$I_1=du^2+(u^2+a^2)dv^2.$$

Вершины треугольника: begin &A(u=0,, v=0),\ &B(u=-frac<2>,, v=1), \ &C(u=frac<2>,, v=1). end

Зная координаты вершин и уравнения сторон, найдем длины дуг, составляющих стороны треугольника $ABC$, и углы между линиями в точках их пересечения, то есть в вершинах треугольника: begin &s_1 = |BC| = a,\ &s_2 = |AC| = frac76 a,\ &s_3 = |BC| = frac76 a,\ &P_<triangle ABC>=s_1+s_2+s_3=frac<10><3>a. end begin &mbox,A = 1, ,, mbox,B=mbox,C=frac23. end

Пересечение прямых, угол и координаты пересечения

IP76 > Пересечение прямых, угол и координаты пересечения

Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x₁-x₂) никак не разделить и т.д.

Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.

Коэффициенты А, B, C

Все помним со школы формулу:

Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):

Те же фаберже, только сбоку.

В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.

Загвоздка в том, что мы не знаем коэффициенты для обеих линий.

В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:

Путем несложных операций приходим к следующей записи:

Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:

Пока все идет отлично, нигде вероятного деления на ноль не встретилось.

Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.

Система уравнений

Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.

Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.

Сразу же запишем метод под нашу систему.

Имеем следующую систему:

Исходя из метода, решение выглядит так:

Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.

Практика 1

Частные случаи

• Прямые параллельны: ∆_ab = 0
  • (A₁B₂ – B₁A₂ = 0);
• Прямые совпадают: ∆_ab = ∆_X = ∆_Y = 0
  • (A₁B₂ – B₁A₂ = 0) И (A₁C₂ — A₂C₁ = 0) И (C₁B₂ -B₁C₂ = 0);
• Прямые перпендикулярны:
  • (A₁ A₂ + B₁ B₂ = 0).

Рис.2. Пересечение перпендикулярных прямых Рис.3. Параллельные прямые не пересекаются

Принадлежность точки отрезку

В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:

1. Точка принадлежит прямой, проходящей через конечные точки отрезка. Для этого достаточно подставить значение X и Y в уравнение прямой и проверить получившееся равенство. В нашем случае, этот пункт уже выполнен, т.к. точка пересечения априори принадлежит обеим прямым.
2. Проверить факт нахождения точки между концами отрезка.

Займемся пунктом 2. Данный факт можно установить двумя способами:

• Логически, т.е. (x₁ = x >= x₂). На случай «вертикальности» линии добавить проверку на Y:
  • (y₁ = y >= y₂).
• Арифметически. Сумма отрезков |x-x₁| + |x-x₂| должна быть равна длине отрезка |x₁-x₂|. Аналогично, на случай «вертикальности» , добавить проверку:
  • |y-y₁| + |y-y₂| = |y₁-y₂|

Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.

Задача нахождения принадлежности точки P(x,y) отрезку, заданного двумя точками с координатами P1(x1, y1) и P2(x2, y2) подробно рассмотрена в отдельной статье.

Угол пересечения прямых

Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p₁ и p₂, получим направляющий вектор V(p₁,p₂), и аналогично второй вектор M(p₃,p₄). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.

Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:

Рис.4. Вектор V(p₁,p₂)

α — угол наклона вектора к оси X, который можно найти, как:

Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…

Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.

Рис.5. Пересекающиеся вектор V(p₁,p₂) и вектор M(p₃,p₄)

Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.

Рис.6. Пересекающиеся векторы в положительной Y

По рисунку явно видно, что угол между векторам это γ = (β — α).

В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.

От теории к практике

Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.

Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.

Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Математический анализ
• Геометрические применения производных.

Геометрический смысл производной.

Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.

Значение производной $f'(x_0)$ функции $y=f(x)$ в точке $x_0$ равно угловому коэффициенту $k=tgvarphi$ касательной $TT’$ к графику этой функции, проведенной через точку $M_0(x_0, y_0),$ где $y_0=f(x_0)$ (геометрический смысл производной).

Прямая $NN’,$ проходящая через точку касания $M_0$ перпендикулярно к касательной, называется нормалью к графику функции $y=f(x)$ в этой точке. Уравнение нормали $$(x-x_0)+f'(x_0)(y-y_0)=0.$$ Уравнение касательной $TT’$ к графику функции $y=f(x)$ в его точке $M_0(x_0, y_0)$ имеет вид $$y-y_0=f'(x_0)(x-x_0)$$

Углом $omega$ между кривыми $y=f_1(x)$ и $y=f_2(x)$ в их общей точке $M_0(x_0, y_0)$ называется угол между касательными к этим кривым в точке $M_0.$ Его можно вычислить по формуле $$tg,omega=frac<1+f’_1(x_0)f’_2(x_0)>.$$

Примеры.

Написать уравнения касательной и нормали к графику функции $y=f(x)$ в данной точке, если:

5.235. $y=x^2-5x+4,$ $x_0=-1.$

Решение.

Уравнение касательной будем искать по формуле $y-y_0=f'(x_0)(x-x_0);$ уравнение нормали — по формуле $(x-x_0)+f'(x_0)(y-y_0)=0.$

По условию, $x_0=-1. $

$y'(x)=2x-5Rightarrow y'(x_0)=y'(-1)=2cdot (-1)-5=-2-5=-7.$

Подставляем все найденные значения в уравнение касательной:

Теперь находим уравнение нормали:

Ответ: У равнение касательной: $7x+y-3=0;$ уравнение нормали: $ x-7y+71=0.$

Решение.

Уравнение касательной будем искать по формуле $y-y_0=f'(x_0)(x-x_0);$ уравнение нормали — по формуле $(x-x_0)+f'(x_0)(y-y_0)=0.$

По условию, $x_0=4. $

Подставляем все найденные значения в уравнение касательной:

$y-2=frac<1><4>(x-4)Rightarrow 4(y-2)=x-4Rightarrow 4y-8=x-4Rightarrow x-4y+4=0.$

Теперь находим уравнение нормали:

$(x-4)+frac<1><4>(y-2)=0Rightarrow 4(x-4)+(y-2)=0Rightarrow 4x+y-18=0.$

Ответ: У равнение касательной: $x-4y+4=0;$ уравнение нормали: $4x+y-18=0.$

5.241. Написать уравнения касательной и нормали в точке $M_0(2, 2)$ к кривой $x=frac<1+t>,$ $y=frac<3><2t^2>+frac<1><2t>,,, tneq 0.$

Найдем значение $t_0,$ подставляя координаты точки $M_0$ в уравнение кривой: $2=frac<1+t>,$ $2=frac<3><2t^2>+frac<1><2t>.$

$t^2+t-2=0Rightarrow t_1=1, t_2=-2.$

Подставим полученные решения в равенство $frac<1+t>=frac<3><2t^2>+frac<1><2t>:$

$t_2=-2: frac<1-2><-8>=frac<3><8>-frac<1><4>=frac<1><8>neq 2$ — не удовлетворяет нашей системе.

Найдем производную функции, заданной параметрически $y’_x.$

Подставляем все найденные значения в уравнение касательной:

$y-y_0=f'(x_0)(x-x_0)Rightarrow$ $y-2=frac<7><10>(x-2)Rightarrow 10(y-2)=7(x-2)Rightarrow 10y-20=7x-14Rightarrow$ $7x-10y+6=0.$

Теперь находим уравнение нормали:

$(x-x_0)+f'(x_0)(y-y_0)=0Rightarrow$ $(x-2)+frac<7><10>(y-2)=0Rightarrow 10(x-2)+7(y-2)=0Rightarrow 10x+7y-34=0.$

Ответ: У равнение касательной: $7x-10y+6=0;$ уравнение нормали: $10x+7y-34=0.$

Найти углы, под которыми пересекаются заданные кривые:

5.254. $y=x^2$ и $y=x^3.$

Решение.

Найдем координаты точки пересечения заданных кривых. Решаем систему уравнений:

$left<begin y=x^2,\ y=x^3,endright.Rightarrow$ $left<begin y=x^2,\ x^2=x^3,endright.Rightarrow$ $left<begin y=x^2,\ x_1=0\x_2=1,endright.$ Таким образом, кривые пересекаются в точках $M_1(0, 0)$ и $M_2(1, 1).$

Далее найдем значения производных заданых функций в точках пересечения.

Подставляем найденные значения, в формулу нахождения угла:

Ответ: В точке $M_1(0, 0)$ угол равен 0. (т.е. касательные совпадают), в точке $M_2(1, 1)$ угол равен $arctgfrac<1><7>.$

Написать уравнения касательной и нормали к графику функции $y=f(x)$ в данной точке, если:

Ответ: У равнение касательной: $y-5=0;$ уравнение нормали: $x+2=0.$

Ответ: У равнение касательной: $y-2x=0;$ уравнение нормали: $2y+x=0.$

Ответ: У равнение касательной: $x-y-1=0;$ уравнение нормали: $x+y-1=0.$

5.242. Написать уравнения касательных к кривой $$x=tcos t, ,,, y=tsin t,,,, tin(-infty,,, +infty),$$ в начале координат и в точке $t=pi/4.$

5.244. Написать уравнения касательной к кривой $$x^5+y^5-2xy=0 в точке $M_0(1, 1).$

Найти углы,под которыми пересекаются заданные кривые:

5.260. Найти расстояние от начала координат до нормали к линии $y=e^<2x>+x^2,$ проведенной в точке с абсциссой $x=0.$

Найти углы, под которыми пересекаются линии,заданные уравнениями :

y [math]=[/math] X[math]^{2}[/math]
X[math]^{2}[/math] [math]+ 2Y[/math] [math]^{2}[/math] [math]= 3[/math]

1.Как я предполагаю, необходимо отыскать точки пересечения этих кривых.
Необходимо составить систему из уравнений и решить ее.

2.Далее находим касательные в этих точках к каждой из линий.

3.Далее из касательных «вытягиваем» направляющие векторы
и скалярное произведение их и выдаст искомый угол.

Но тут, при составлении системы уравнений для поиска точек пересечения,
образуется уравнение четвертой степени. Которое наводит меня на мысль,
что я усложняю простое.
Подскажите, может быть есть иной путь решения подобных задач. Более простой.