Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
Как найти угол между вектором и осью абсцисс
Проекция вектора на ось есть скалярная величина, равная произведению модуля проектируемого вектора на косинус угла между положительными направлениями оси и вектора (см. рисунок).
Проекция вектора на ось обозначается через al или , а угол между осью и вектором будем обозначать так: . Таким образом,
(2)
Если — углы, образованные вектором с координатными осями Ox, Oy и Oz прямоугольной системы координат, то проекции вектора на координатные оси будут равны
(3)
В дальнейшем предполагается, что система координат — прямоугольная.
Модуль вектора через его проекции на оси прямоугольной системы координат вычисляется по формуле
(4)
т. е. модуль вектора равен арифметическому значению квадратного корня из суммы квадратов его проекций.
Вектор равен нулю, если все три его проекции равны нулю (этим положением пользуются, например, в механике при выводе необходимых и достаточных условий равновесия тела под действием системы сил, проходящих через одну точку).
Угол между векторами.
Формула вычисления угла между векторами
| cos α = | a · b |
| | a |·| b | |
Примеры задач на вычисление угла между векторами
Примеры вычисления угла между векторами для плоских задачи
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5
Найдем угол между векторами:
| cos α = | a · b | = | 24 | = | 24 | = 0.96 |
| | a | · | b | | 5 · 5 | 25 |
Решение: Найдем скалярное произведение векторов:
a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.
Найдем модули векторов:
| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
| cos α = | a · b | = | 40 | = | 40 | = | 4 | = 0.8 |
| | a | · | b | | 5√ 2 · 5√ 2 | 50 | 5 |
Примеры вычисления угла между векторами для пространственных задач
Решение: Найдем скалярное произведение векторов:
a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.
Найдем модули векторов:
| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6
Найдем угол между векторами:
| cos α = | a · b | = | 28 | = | 14 |
| | a | · | b | | 5 · 6 | 15 |
Решение: Найдем скалярное произведение векторов:
a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.
Найдем модули векторов:
| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2
Найдем угол между векторами:
cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
http://www.pm298.ru/reshenie/vektor4.php
http://ru.onlinemschool.com/math/library/vector/angl/
Алгебра и начала математического анализа, 11 класс
Урок №52. Производная и интеграл.
Перечень вопросов, рассматриваемых в теме:
- задачи, решаемые с применением производной
- задачи, решаемые с применением первообразной и интеграла
Глоссарий по теме
Производной функции в данной точке называется предел разностного отношения:
Уравнение касательной к графику данной функции в данной точке y=f(x)+f ‘(x0)(x-x0)
Функция у=f(x) возрастает на промежутке (a; b), если для любых х1, х2 из этого промежутка, таких, что х1<х2, выполняется неравенство у1<у2. Иными словами, меньшему значению аргумента соответствует меньшее значение функции.
Функция у=f(x) убывает на промежутке (a; b), если для любых х1, х2 из этого промежутка, таких что, х1<х2, выполняется неравенство у1>у2. Иными словами, меньшему значению аргумента соответствует большее значение функции.
Промежутки возрастания и убывания функции называют промежутками монотонности этой функции. Слова «функция монотонна на данном промежутке» означают, что функция на этом промежутке возрастает или убывает.
Точка х1 называется точкой максимума функции f, если для всех х из окрестности точки х1 выполняется неравенство f(x)<f(x1).
Точка х2 называется точкой минимума функции f, если для всех х из окрестности точки х2 выполняется неравенство f(x)>f(x2).
Для точек максимума и минимума принято общее название – точки экстремума.
Значения функции в этих точках называют соответственно максимумами и минимумами. Их общее название – экстремум функции.
Функция F(x) называется первообразной для функции f(x) на промежутке (a; b), если f(x)=F'(x) в каждой точке промежутка (a; b).
Дифференциальные уравнения связывают функцию и ее производные различных порядков. В дифференциальном уравнении в качестве неизвестной выступает не число, а функция.
Решением дифференциального уравнения называют любую функцию, при подстановке которой в это уравнение получается тождество.
Фигура, ограниченная графиком неотрицательной функции f(x), заданной на отрезке [a; b], отрезком [a; b] и прямыми x=a и x=b, называется криволинейной трапецией.
Разность значений первообразной F для функции f точках b и a называется определенным интегралом этой функции от a до b.
Основная литература:
Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е., Шабунин М.И. под ред. Жижченко А.Б. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни– 2-е изд. – М.: Просвещение, 2010.
Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 11 класса: Учеб. пособие для учащихся шк. и классов с углубл. изуч. математики — 4-е изд. — М.: Просвещение, 1995. — 288 с.: ил. — ISBN 5-09-0066565-9, сс. 7-50
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.
Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.
Федеральный центр информационно-образовательных ресурсов http://fcior.edu.ru/
Единая коллекция цифровых образовательных ресурсов http://school-collection.edu.ru/
Теоретический материал для самостоятельного изучения
1. Определение производной
Напомним, что производной функции в заданной точке называется предел разностного отношения:
Напомним правила вычисления производных:
Приведем пример:
Найти производную функции:
Решение:

Ответ: 
2. Решение задач с помощью производной.
Напомним, что геометрический смысл производной — это угловой коэффициент касательной. Те есть значение производной в данной точке равно угловому коэффициенту касательной к графику функции в заданной точке: f'(x0)=kкас.(x0)
Задача 1.
Найдем угол, под которым график функции 
Найдем производную данной функции: 
Так как нам нужно узнать угол, под которым график функции пересекает ось абсцисс, нам нужно найти эти точки пересечения. Для этого решим уравнение: 
То есть график данной функции пересекает ось абсцисс в трех точках с найденными абсциссами.
Угол пересечения графика функции оси абсцисс — это угол, под которым касательная, проведенная к графику данной функции в точке с соответствующей абсциссой, пересекает ось абсцисс.
Угловой коэффициент касательной — это тангенс угла наклона касательной к оси абсцисс. Поэтому нужно найти значение производной данной функции в точках пересечения ее графика с осью абсцисс.
Найдем углы:





Вспомним механический смысл производной.
Производная — это скорость материальной точки, положение которой изменяется по заданному закону.
Решим задачу 2.
Движение материальной точки описывается данным уравнением:
x(t) = 4+5t – 6t2 + 2t3.
Найти скорость и ускорение точки в момент времени 3.
a(t)=-12+12·3=24.
Ответ: v=23; a=24.
Теперь напомним решение задачи на наибольшее и наименьшее значение, которая также решается с помощью производной.
Задача 3.
Найти прямоугольник наибольшей площади, вписанный в окружность радиуса R.
Решение:
Рисунок 1 — Иллюстрация к задаче 3




Исследуем функцию 






При
Прямоугольником наибольшей площади, вписанным в круг радиуса R, является квадрат со стороной 
3. Теперь перейдем к повторению первообразной и интеграла.
Функция F(x) называется первообразной для функции f(x) на промежутке (a; b), если f(x)=F'(x) в каждой точке промежутка (a; b).
Все первообразные для данной функции отличаются друг от друга на константу
Пример.
Покажем, что функция 

Найдем производную: 
Преобразуем полученную функцию:

Получили функцию f(x).
4. Решение задач
Задача 4.
Найдите первообразную для функции 
Решение:
Для функции 


По условию: F(1)=6
С=5,4
Ответ: 
Задача 5.
Точка движется прямолинейно с ускорением

Так как 
Так как 




Ответ: 
Задача 6.
Вычислите объем тела, ограниченного плоскостями x=0, x=0,5 , площадь сечения которого плоскостью, параллельной плоскости yOz и отстоящей от нее на расстоянии х, меняется по закону:
Решение:


Задача 7.
Найдите площадь фигуры, ограниченной графиками следующих функций.

Решение:
Рисунок 2 — Иллюстрация к задаче 6.


Ответ: 7,5 кв.ед.
Примеры и разбор решения заданий тренировочного модуля
1. Найдите аргумент, при котором функция 
Решение:
Найдем производную данной функции, сначала преобразуем функцию, выделив целую часть: 
Теперь найдем производную:

Полученная производная изменяет свой знак в точках 2 и -2, в точке 0 функция и производная не определены.
Так как задан отрезок [-3; -1], то рассмотрим поведение производной вокруг точки -2.
Так как на данном отрезке функция имеет единственную точку экстремума (максимум), то наибольшее значение она принимает в этой точке.
Ответ: -2
2. Вычислите массу участка стержня от x_1


Решение:
Масса участка стержня на заданном участке выражается интегралом: 
Для того чтобы найти массу участка стержня от 



Ответ: 
3. Найти путь, пройденный при свободном падении телом за первые 5 секунд (ускорение равно 9,8 м/с2)
Решение.
Скорость в момент времени t равна 9,8t.
Значит, путь, пройденный за промежуток времени [0; 5], выражается определенным интегралом:

-
1
Угловой коэффициент равен тангенсу угла между прямой и положительным направлением оси абсцисс. Чем больше угловой коэффициент, тем быстрее растет функция.
-
2
Отрицательный угловой коэффициент свидетельствует об убывающей функции, а положительный — о возрастающей.
-
3
Угловой коэффициент прямой, параллельной оси Х, всегда равен нулю, а угловой коэффициент прямой, параллельной оси Y, не существует.
Реклама
-
1
На графике отметьте любые две точки, координаты которых вы сможете найти.
-
2
Через точки проведите прямые, параллельные оси Х и оси Y.
- Точки пересечения этих прямых будут лежать над и под графиком, образуя два прямоугольных треугольника. Рассмотрите любой из этих треугольников.
- Точки пересечения этих прямых будут лежать над и под графиком, образуя два прямоугольных треугольника. Рассмотрите любой из этих треугольников.
-
3
Выберите точку, лежащую на графике справа, и найдите расстояние между этой точкой (исходная точка) и точкой пересечения (конечная точка) прямых, параллельных координатным осям.
- То есть вам нужно посчитать количество делений на оси Y от исходной точки до конечной точки. Например, количество делений равно 5.
- Теперь выберите точку, лежащую на графике слева, и найдите расстояние между этой точкой (исходная точка) и точкой пересечения (конечная точка) прямых, параллельных координатным осям. То есть вам нужно посчитать количество делений на оси Х от исходной точки до конечной точки. Например, количество делений равно 7.
- То есть вам нужно посчитать количество делений на оси Y от исходной точки до конечной точки. Например, количество делений равно 5.
-
4
Угловой коэффициент равен отношению количества делений на оси Y к количеству делений на оси Х; в нашем примере угловой коэффициент равен 5/7.
-
5
Если возможно, упростите полученную дробь.
Реклама
-
1
Если вы знаете координаты точек ((x1, y1) и (x2, y2)), лежащих на графике, то вы можете вычислить угловой коэффициент по формуле:
(y2 — y1) / (x2 — x1)
или
(y1 — y2) / (x1 — x2)Обе формулы эквивалентны.
-
2
Допустим, даны точки с координатами (-4, 7) и (-1, 3).
-
3
Подставьте координаты в формулу.
-
4
Упростите полученную дробь (если это возможно).
Реклама
Советы
- Если вы не знакомы, почему (-4) — (-1) = -3, то прочитайте эту статью.
- Формула: k = (y2 — y1)/(x2 — x1)
где k – угловой коэффициент, (x1, y1) и (x2, y2) – координаты двух точек.
Реклама
Об этой статье
Эту страницу просматривали 27 329 раз.
Была ли эта статья полезной?
Под углом между прямой и осью абсцисс
принимается угол
между направляющим вектором
прямой
и ортом
оси
. Для данной прямой
Угол с осью
определим из формулы

Аналогично определяются углы и
между прямой
и осями
и
:

Величины называются Направляющими косинусами прямой
.
Пример. Найти углы, образуемые прямой
С осями координат.
Решение. Найдем координаты направляющего вектора, как векторное произведение нормалей к данным плоскостям и
. Координаты нормальных векторов плоскостей
и
:

.
Используя формулы (1)-(2), получим

Следовательно,
| < Предыдущая | Следующая > |
|---|
Калькулятор углового коэффициента прямой может не только рассчитать коэффициент, но и найдет точки пересечения прямой с осями абсцисс и ординат (x и y), а также покажет решение и построит график прямой.
Содержание:
- калькулятор углового коэффициента прямой
- определение углового коэффициента прямой
- формула углового коэффициента прямой
- геометрический смысл углового коэффициента
- k>0
- k<0
- k=0
- k не определен (k=∞)
- угловой коэффициент параллельных прямых
- угловой коэффициент перпендикулярных прямых
- примеры расчета углового коэффициента прямой по заданным координатам точек
Определение углового коэффициента прямой
Угловой коэффициент прямой — это число, которое определяет наклон прямой относительно положительного направления оси OX. Численно он равен тангенсу угла (отсчитываемого против часовой стрелки) между положительным направлением оси OX и прямой.
Угловой коэффициент прямой обозначается буковой k.
Угловой коэффициент показывает, как быстро прямая меняет свое положение по оси OX при изменении координаты y и является ключевым понятием в геометрии и физике, используемым для описания многих физических явлений, например, движения тела в пространстве или распространение света.
В геометрии, угловой коэффициент прямой используется для определения угла наклона прямой относительно оси абсцисс и для вычисления ее точек пересечения с осями координат. Также угловой коэффициент прямой используется для записи уравнения прямой в общем виде. Знание углового коэффициента прямой является необходимым при решении многих задач геометрии, таких как построение перпендикуляров и параллельных линий, определение углов между прямыми и плоскостями, а также решение задач на поиск расстояний между прямыми и плоскостями.
Формула углового коэффициента прямой
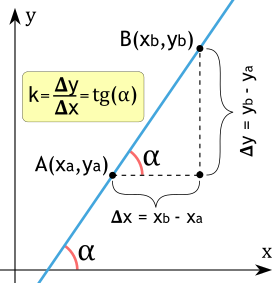
Формула вычисления углового коэффициента прямой определяется как отношение изменения координаты y к изменению координаты x между любыми двумя точками на прямой. Математически это можно записать следующим образом:
{k=dfrac{y_b — y_a}{x_b — x_a} = tg(alpha)}
k — угловой коэффициент прямой,
xa, ya — координаты точки A,
xb, yb — координаты точки B
α — угол между осью OX и прямой (против часовой стрелки).
Если прямая задана уравнением в общем виде y = kx + b, то угловой коэффициент прямой равен коэффициенту при x, то есть k.
Геометрический смысл углового коэффициента прямой
Рассмотрим возможные значения углового коэффициента и какой геометрический смысл он несет.
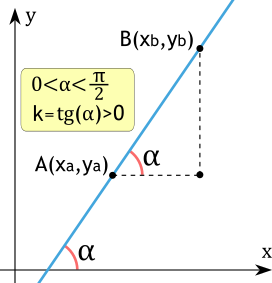
Угловой коэффициент прямой больше нуля
Если угловой коэффициент прямой больше нуля (k>0), то угол между осью OX и прямой является острым, а график прямой возрастающий. Обратное утверждение также справедливо — если график прямой возрастает, то ее угловой коэффициент больше нуля.
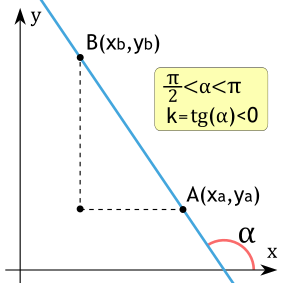
Угловой коэффициент прямой меньше нуля
Если угловой коэффициент прямой меньше нуля (k<0), то угол между осью OX и прямой является тупым, а график прямой убывающий. И наоборот — если график прямой убывает, то ее угловой коэффициент меньше нуля.
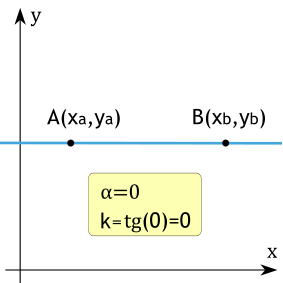
Угловой коэффициент равен нулю
Если угловой коэффициент прямой равен нулю (k=0), то это значит, что прямая параллельна оси x.
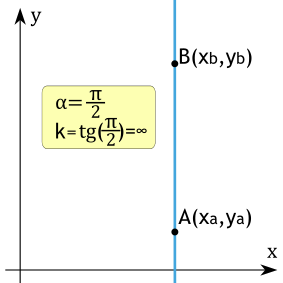
Угловой коэффициент не определен (равен бесконечности)
Если угловой коэффициент прямой не определен (или можно сказать обращается в бесконечность) (k=∞), то это значит, что прямая параллельна оси y.
Угловой коэффициент параллельных прямых
Если прямые параллельны, то их угловые коэффициенты равны и наоборот — если у прямых равные угловые коэффициенты, то они параллельны друг другу.
Угловой коэффициент перпендикулярных прямых
Если прямые перпендикулярны, то их угловые коэффициенты обратно пропорциональны и имеют противоположный знак.
Для примера рассмотрим две прямые, заданные угловыми коэффициентами:
y = k_{m} x + b_m
y = k_{n} x + b_n
Прямые будет перпендикулярны, если k_{m} = — dfrac{1}{k_{n}}
Как рассчитать угловой коэффициент прямой по заданным координатам точек
Чтобы закрепить материал, рассмотрим решение задачи.
Задача 1
Найдите угловой коэффициент прямой, проходящей через точки A(5, -2) и B(-3, 1).
Решение
Воспользуемся формулой углового коэффициента прямой. Для начала найдем разницу между соответствующими координатами двух точек:
{Delta x = x_b — x_a = -3 -5 -= -8}
{Delta y = y_b — y_a = 1 — -(2) = 3}
Осталось применить формулу и поделить Delta y на Delta x:
k = dfrac{Delta y}{Delta x} = dfrac{3}{-8} = — dfrac{3}{8} approx -0.375
Это и есть угловой коэффициент прямой AB.
А если вы внимательно читали статью, то, учитывая, что полученный угловой коэффициент отрицательный, можно сказать, что прямая AB убывающая.
Ответ: k = — dfrac{3}{8} approx -0.375
Проверить ответ нам поможет калькулятор .