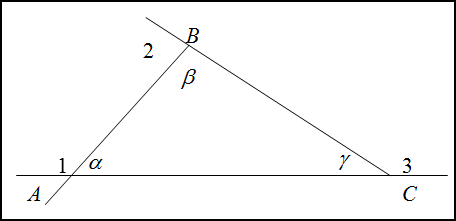
Углы треугольника
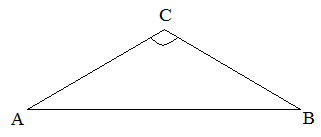
Треугольники делятся на остроугольные (у которых все углы острые), тупоугольные (один угол тупой) и прямоугольные (один угол равен 
).
Угол смежный с внутренним углом треугольника называется внешним углом.
![[angle 4=angle 1+angle 2]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d6678c9ce3acacdf0b136ff260b4e8cb_l3.png)
Примеры решения задач
![[angle A +angle B=180-91^{circ} =89^{circ} ,]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-50a7367e36d61162ffdf4549fd3c5c34_l3.png)
т.е. каждый из углов А и В заведомо меньше угла С. Это значит, что против угла С лежит большая сторона треугольника. Используя условие задачи, можно записать следующее неравенство:
![[AC<BC<AB,]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-63a9f2e31e42df2a728d1766ef23ed25_l3.png)
т.е. сторона 
имеет наименьшую длину.
![[angle B=180^{circ} -angle A-angle C=50^{circ} ]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-0213fccbe3150eef4b65ae04b1b26b74_l3.png)
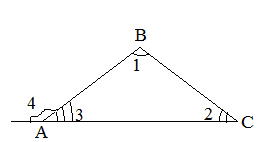
Внешний угол при вершине 
равен сумме внутренних углов при вершинах 
и 
, т.е. равен 
. Аналогично получаем, что внешний угол при вершине равен 
, а внешний угол при вершине равен 
.
Внешний угол треугольника
Внешний угол треугольника — это угол, смежный с любым из внутренних углов треугольника.
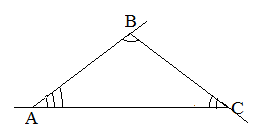
При каждой вершине треугольника может быть построено по два равных внешних угла. Например, если продолжить все стороны треугольника ABC, то при каждой его вершине получится по два внешних угла, которые равны между собой, как вертикальные углы:
Из данного примера можно сделать вывод, что внешние углы, построенные при одной вершине, будут равны.
Внешний угол треугольника равен сумме двух внутренних углов треугольника, не смежных с ним.
Так как внешний угол (∠1) дополняет внутренний угол (∠4) до развёрнутого угла, то их сумма равна 180°:
Сумма внутренних углов углов любого треугольника тоже равна 180°, значит:
Из этого следует, что
Сократив обе части полученного равенства на одно и тоже число (∠4), получим:
Из этого можно сделать вывод, что внешний угол треугольника всегда больше любого внутреннего угла, не смежного с ним.
Сумма внешних углов
Сумма трёх внешних углов треугольника, построенных при разных вершинах, равна 360°
Рассмотрим треугольник ABC:
Каждая пара углов (внутренний и смежный с ним внешний) в сумме равны 180°. Все шесть углов (3 внутренних и 3 внешних) вместе равны 540°:
Значит чтобы найти сумму внешних углов, надо из общей суммы вычесть сумму внутренних углов:
Как найти внутренний угол
Для нахождения внутреннего угла треугольника вспомните теорему о сумме углов треугольника.
Теорема: сумма углов треугольника равна 180°.
Из этой теоремы выделите пять следствий, которые могут помочь в расчете внутреннего угла.
1. Сумма острых углов прямоугольного треугольника равна 90°.
2. В равнобедренном прямоугольном треугольнике каждый острый угол равен 45°.
3. В равностороннем треугольнике каждый угол равен 60°.
4. В любом треугольнике либо все углы острые, либо два угла острые, а третий тупой или прямой.
5. Внешний угол треугольника равен сумме двух внутренних углов.
Пример 1:
Найти углы треугольника АВС, зная, что угол С на 15° больше, а угол И на 30° меньше угла А.
Решение:
Обозначьте градусную меру угла А через Х, тогда градусная мера угла С равна Х+15°, а угол В равен Х-30°. Так как сумма внутренних углов треугольника равна 180°, то вы получите уравнение:
Х+(Х+15)+(Х-30)=180
Решая его, вы найдете Х=65°. Таким образом угол А равен 65°, угол В равен 35°, угол С равен 80°.
Еще для нахождения внутреннего угла вы можете использовать равенство треугольников:
Теорема 1: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
На основе Теоремы 1 устанавливается Теорема 2.
Теорема 2: Сумма любых двух внутренних углов треугольника меньше 180°.
Из предыдущей теоремы вытекает Теорема 3.
Теорема 3: Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Также для вычисления внутреннего угла треугольника можно использовать теорему косинусов, но только в том случае, если известны все три стороны.
- вычислить внутренние углы треугольника
- Как по сторонам треугольника узнать угол
- Как найти углы треугольника по сторонам
- Как вычислить угол в треугольнике
to continue to Google Sites
Not your computer? Use Guest mode to sign in privately. Learn more
Треугольник – это форма многоугольника, которая имеет три угла, образованных тремя сторонами. Каждая
из трех точек, в которых пересекаются стороны треугольника, называется его вершиной и образует
определенный угол. Стороны треугольника иногда еще называют линейными длинами, а углы – угловыми.
Сторону, противоположную определенному углу, обозначают той же буквой, что характеризует угол как
прилегающий. Стороны обозначаются латинскими буквами a, b, c, а углы – греческими α, β, γ. Зная
определенные параметры треугольника, можно найти его стороны и углы. При этом можно использовать как
линейные формулы, так и обращаться к различным теоремам, например, теореме синусов и косинусов.
- Угол треугольника через три стороны
- Угол прямоугольного треугольника через две стороны
- Угол треугольника через высоту и катет
- Угол при основании равнобедренного треугольника через
биссектрису и боковую сторону - Угол при основании равнобедренного треугольника через
биссектрису и основание - Угол между боковыми сторонами равнобедренного треугольника
через биссектрису и боковую сторону - Острый угол прямоугольного треугольника через катет и
площадь - Острый угол между боковыми сторонами равнобедренного
треугольника через площадь и боковую сторону
Угол треугольника через три стороны
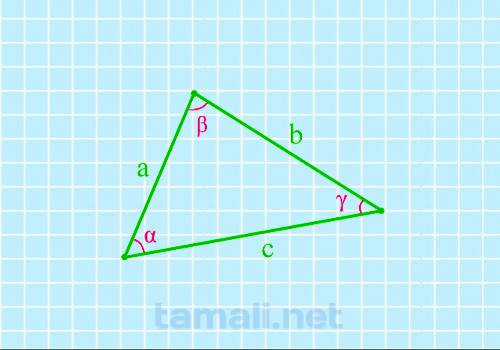
Для того, чтобы найти угол по трем сторонам, нужно вычислить косинус определенного угла. Согласно
теореме косинусов, «квадрат длины стороны треугольника равен сумме квадратов двух других длин его
сторон, минус удвоенное произведение этих длин сторон на косинус угла между ними». Если взять за
предмет вычисления угол β, соответственно, получаем формулу: a² = b² + c² — 2 · b · c · cos (β).
Из полученного равенства можно вычислить
cos(α) = (a² + c² — b²) / 2ac
cos(β) = (a² + b² — c²) /
2ab
cos(γ) = (b² + c² — a²) / 2cb
где a, b, c — стороны треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть a = 3, b = 7, c = 6. Cos (β) = (7² + 6² — 3²) : (2 · 7 · 6) = 19/21.
Зная косинус, нужно воспользоваться таблицей Брадиса и по ней найти угол. По таблице Брадиса, если
Cos (β) = 19/21, то β = 58,4°.
Угол прямоугольного треугольника через две стороны
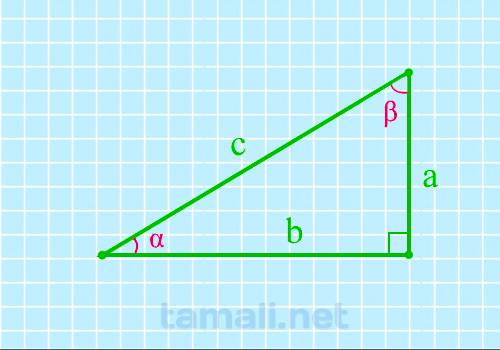
Если известен катет и гипотенуза, угол вычисляется через синус. Если известны катеты и нужно найти
один из острых углов, то можно сделать это через вычисление тангенса.
sin(α) = cos (β) = a / c
sin(β) = cos (α) = b / c
tg(α) = ctg(β) = a
/ b
tg(β) = ctg(α) = b / a
где a, b — катеты, c — гипотенуза.
Цифр после запятой:
Результат в:
Пример. В прямоугольном треугольнике есть два катета a = 12, b = 9 и гипотенуза c =
15. Если известны катеты и нужно найти один из острых углов, то можно сделать это через вычисление
тангенса: tg(α) = a / b, то есть tg(α) = 12 / 9. По таблице Брадиса, угол
α = 53, 13°. Если известен катет и гипотенуза, угол вычисляется через синус sin(α) = a / c = 12 / 15 = 0,8. В
этом случае по таблице Брадиса для синусов и косинусов, значение угла – 36, 87°.
Острый угол прямоугольного треугольника через катет и площадь
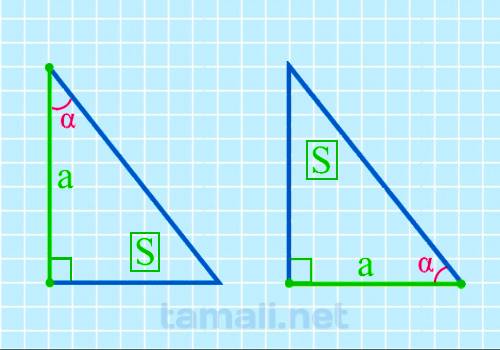
Для того, чтобы вычислить размер острого угла, нужно образовать обратную формулу от площади
прямоугольного треугольника, которая вычисляется через катет и острый угол. Выглядит она следующим
образом: S = (a² * tg β) / 2. Из этих показателей известный площадь S и катет a. Отсюда формула для
нахождения угла будет следующая:
tg(α) = a² / 2S
где a — катет, S — площадь прямоугольного треугольника.
Цифр после
запятой:
Результат в:
Пример. Пусть S = 34, a = 8. Получается следующее уравнение: tg(α) = a² / 2S = 8² + 2 * 34 = 132.
Таким образом выходит, что по таблице Брадиса, угол с таким тангенсом равен 43°.
Угол треугольника через высоту и катет
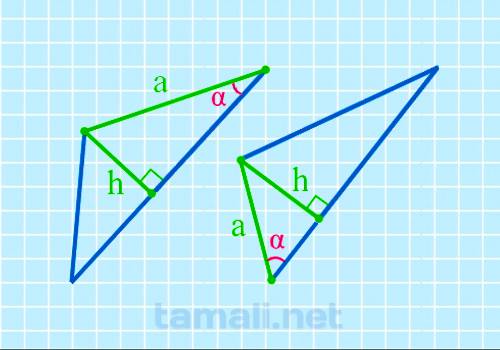
В некоторых прямоугольных треугольниках, в основании которых один острый угол, а второй 90°, один из
катетов (вертикальная прямая, образующая прямой угол) называется также высотой и обозначается как h.
Второй катет a остается со своим обычным названием.
sin α = h / a
где h — высота, a — катет.
Цифр после запятой:
Результат в:
Пример. Если высота h = 8, а катет a = 10, то угол α находится по формуле sin α = h / a = 8 / 10 = 0.8 то по таблице Брадиса составляет 53°
Угол при основании равнобедренного треугольника через биссектрису и основание
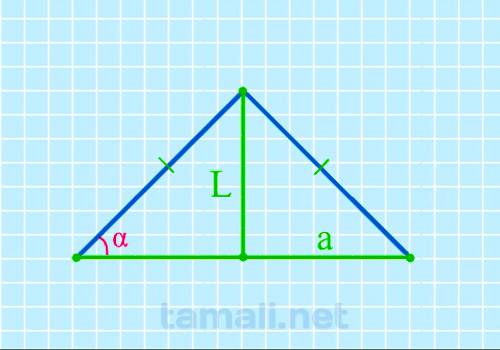
Равнобедренный треугольник ABC с основанием AC имеет биссектрису L (она же CK, делящая основание AC
на два отрезка AK и KB). Также биссектриса L делит угол BCA (он же γ) пополам (каждый из этих
половинок угла γ обозначается как x). То есть γ = 2х. Угол BAC (он же α) = BCA (он же γ), то есть α
= γ. При этом биссектриса L (она же CK) образовала в равнобедренном треугольнике ABC новый
равнобедренный треугольник AKC, в котором AK – это основание, а углы KAC и AKC равны между собой и
равны значению угла γ. Учитывая то, что угол γ равен 2х (то есть двум половинкам угла), то для
треугольника AKC, чтобы вычислить углы при основании, формула будет следующая:
tg α = L / (a/2)
где L — биссектриса, a — основание.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, основание а равно 45, подставив в формулу
получим tg α = L / (a/2) = 15 / (45/2) = 33.69º
Угол при основании равнобедренного треугольника через биссектрису и боковую сторону
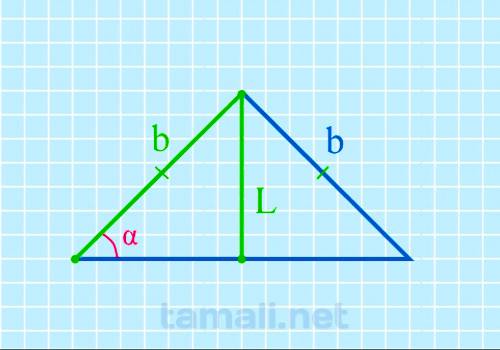
Допустим, что у равнобедренного треугольника ABC углы при основании A (α) и C (γ) равны. Также AB =
BC. Биссектриса L берет начало из вершины А и пересекается с основанием АС, образуя точку
пересечения K, поэтому биссектрису L также можно называть АK. L разделила угол А пополам и основание
поделила на два отрезка: BK и KC. Образовался угол AKC = α (внешний угол для треугольника ABK).
Согласно свойствам внешнего угла:
sin α = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. Пусть биссектриса L равна 15, боковая сторона b равна 30, подставив в
формулу получим sin α = L / b = 15/30 = 30º.
Угол между боковыми сторонами равнобедренного треугольника через биссектрису и боковую сторону
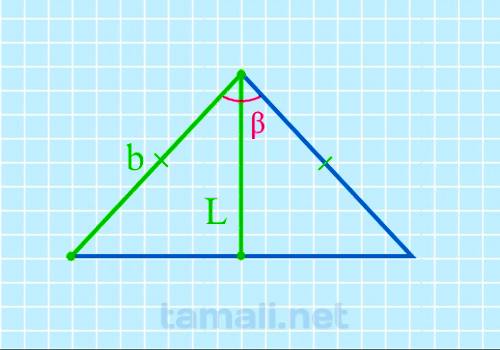
В равнобедренном треугольнике угол ABC (он же β) – это вершина треугольника. Стороны AB и BC равны, и
углы у основания BAC (α) и BCA (γ) тоже равны между собой. Биссектриса L берет начало из вершины B и
пересекается с основанием AC в точке K. Биссектриса BK разделила угол β пополам. Кроме того,
биссектриса разделила треугольник ABC на два прямоугольных треугольника ABK и CBK, так как углы BKA
и BKC – прямые и оба по 90°. Так как треугольники ABK и CBK зеркально одинаковые, для определения
угла β можно взять любой из них. В свою очередь биссектриса BK разделила угол β пополам, например,
на два равных угла х. Оба треугольника, образовавшихся внутри равнобедренного из-за биссектрисы,
прямоугольные, поэтому, чтобы вычислить угол β (он же 2х), нужно взять за правило вычисление угла
через высоту (она в данном случая является также биссектрисой) и катет (это отрезок AK или KC,
которые также равны между собой, так как биссектриса и основание равнобедренного треугольника также
поделила пополам).
2cos(β) = L / b
где L — биссектриса, b — боковая сторона.
Цифр после
запятой:
Результат в:
Пример. В треугольнике BKC известна биссектриса L = 47 см и боковая сторона b = 64
см. Подставив значения в формулу получим: 2cos(β) = L / b = 47 / 64 = 85.49º
Острый угол между боковыми сторонами равнобедренного треугольника через площадь и боковую
сторону
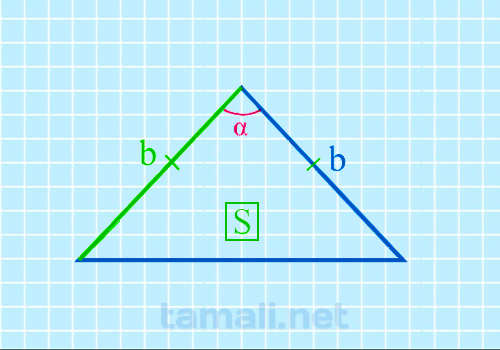
Формула площади равнобедренного треугольника S = 1/2 * bh, где b – это
основание треугольника, а h – это медиана, которая разделила равнобедренный треугольника на два
прямоугольных. Формула для нахождения угла между боковыми сторонами через площадь и боковую сторону
будет следующая:
sin(α) = 2S / b²
где b — боковая сторона равнобедренного треугольника, S — площадь.
Цифр после
запятой:
Результат в:
Пример. Если площадь равна 48, а сторона 10, то угол между боковыми сторонами можно
вычислить следующим образом: sin(α) = 2S / b² = 2 * 48 / 10² = 73.7º
Вне зависимости от условия задачи, известно, что сумма всех углов треугольника составляет 180°.
Поэтому, элементарно вычислить один из углов можно, когда известны два других. Но для вычисления
углов могут быть использованы и другие показатели. Например, для того, чтобы находить стороны и углы
треугольников, в них можно проводить дополнительные меридианы, биссектрисы, чертить окружности и
использовать эти фигуры как дополнительные вводные, через которые по формулам находятся
неизвестные.
Углы очень удобно вычислять через синусы, косинусы, тангенсы и котангенсы, после чего сопоставлять
данные с таблицей Брадиса, в которой эти величины можно сконвертировать в градусы.
В данной публикации мы рассмотрим одну из основных теорем в геометрии 7 класса – о внешнем угле треугольника. Также разберем примеры решения задач, чтобы закрепить представленный материал.
Определение внешнего угла
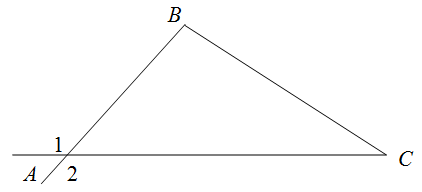
Для начала вспомним, что такое внешний угол. Допустим у нас есть треугольник:
Смежный с внутренним углом (λ) треугольника угол при той же вершине является внешним. На нашем рисунке он обозначен буквой γ.
При этом:
- сумма данных углов равна 180 градусам, т.е. γ + λ = 180° (свойство внешнего угла);
- 0 и 0.
Формулировка теоремы
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
γ = α + β
Из данной теоремы следует, что внешний угол треугольника больше любого из несмежных с ним внутренних углов.
Примеры задач
Задание 1
Дан треугольник, в котором известны значения двух углов – 45° и 58°. Найдите внешний угол, смежный с неизвестным углом треугольника.
Решение
Воспользовавшись формулой теоремы получаем: 45° + 58° = 103°.
Задание 1
Внешний угол треугольника равен 115°, а один из несмежных с ним внутренних углов – 28°. Вычислите значения оставшихся углов треугольника.
Решение
Для удобства будем использовать обозначения, указанные на рисунках выше. Известный внутренний угол примем за α.
Исходя из теоремы: β = γ – α = 115° – 28° = 87°.
Угол λ является смежным с внешним, а значит вычисляется по следующей формуле (следует из свойства внешнего угла): λ = 180° – γ = 180° – 115° = 65°.
Содержание:
- Определение внешнего угла треугольника
- Свойства внешних углов треугольника
- Примеры решения задач
Определение внешнего угла треугольника
Определение
Углы, смежные с углами треугольника, называются внешними.
Например, для $angle A$, внешними будут углы $angle 1$ и $angle 2$ (см. рис.)
Свойства внешних углов треугольника
- Сумма внешних углов треугольника, взятых по одному при каждой вершине, равна $360^{circ}$.
- Сумма внешнего и внутреннего угла при одной вершине равна $180^{circ}$.
-
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
$$angle 1=angle B+angle C$$
Примеры решения задач
Пример
Задание. В треугольнике $Delta M N K$, внешний угол $angle M$ равен $120^{circ}$,
а угол $angle N=65^{circ}$. Найти угол $angle K$.
Решение. По теореме о внешнем угле
$angle M=angle N+angle K$. Подставляя в это равенство исходные данные, получим
$$120^{circ}=65^{circ}+angle K$$
Выразим $angle K : angle K=120^{circ}-65^{circ} Rightarrow angle K=55^{circ}$
Ответ. $angle K=55^{circ}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Внешние углы при двух вершинах треугольник равны $70^{circ}$ и $150^{circ}$.
Найти внутренний угол при третьей вершине.
Решение. Обозначим внешние углы $angle 1, angle 2, angle 3$, а соответствующие им
внутренние — $alpha, beta, gamma$.
По условию $angle 1=150^{circ}$ и $angle 2=70^{circ}$. По свойству внешних углов, их сумма,
взятых по одному при каждой вершине, равна $360^{circ}$. То есть
$$angle 1+angle 2+angle 3=360^{circ}$$
Выразим из этого равенства неизвестный угол $angle 3$
$$angle 3=360^{circ}-angle 1-angle 2$$
$$angle 3=360^{circ}-150^{circ}-70^{circ}$$
$$angle 3=140^{circ}$$
Тогда искомый внутренний угол можно найти из условия, что сумма внутреннего и внешнего углов равна
$180^{circ}$, то есть $gamma+angle 3=180^{circ}$, тогда:
$$gamma=180^{circ}-angle 3$$
$$gamma=180^{circ}-140^{circ}=40^{circ}$$
Ответ. $gamma=40^{circ}$
Читать дальше: что такое медиана треугольника.