Лекция № 11. Пересечение поверхности тел вращения проецирующей плоскостью
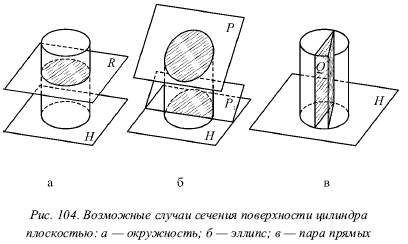
Бывают следующие случаи сечения поверхности прямого кругового цилиндра плоскостью:
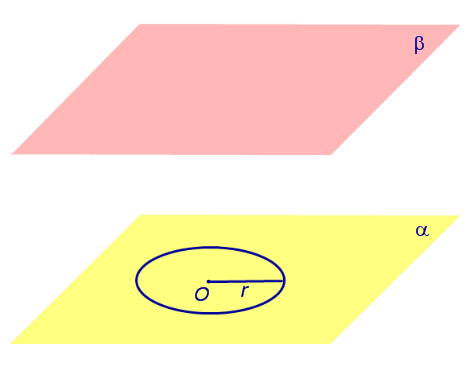
1) окружность, если секущая плоскость Р перпендикулярна оси цилиндра, причем она параллельна основанию цилиндра (рис. 104а);
2) эллипс, если секущая плоскость Р не перпендикулярна и не параллельна оси цилиндра (рис. 104б);
3) пара прямых, если секущая плоскость Q содержит ось цилиндра или параллельна ей (рис. 104в).
Особый интерес представляет случай, когда наклонная секущая плоскость пересекает основание цилиндра (плоскость Р1 на рис. 104б). Здесь часть эллипса может быть неверно принята за параболу или гиперболу. Нужно знать, что ни парабола, ни гипербола не могут быть получены как сечение поверхности кругового цилиндра плоскостью.
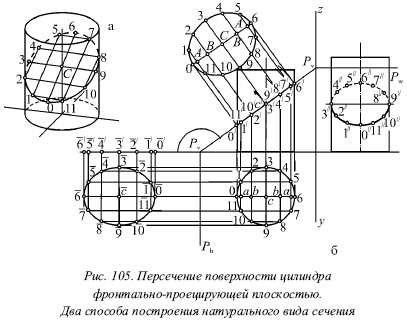
На рисунке 105 показано пересечение поверхности цилиндра фронтально‑проецирующей плоскостью Р. Здесь для цилиндра рассмотрено решение всех трех основных задач, связанных с сечением тела плоскостью, т. е. отыскание проекций сечения, его натурального вида и построение развёртки.
Проекции сечения. На рисунке 105а рассмотрено наглядное изображение сечения, а отсюда видно, что большая ось эллипса представлена хордой 0–6, которая пересекает ось цилиндра в точке С. При этом малая ось направлена по горизонтали, перпендикулярной в плоскости V. Следовательно, малая ось проектируется без искажения на горизонтальной и профильной плоскости (рис. 105б), а центр эллипса находится на оси цилиндра (точка С). Следует отметить, что на рисунке 105б ось симметрии проходит через точки 0–6.
Получающийся в горизонтальном сечении эллипс проецируется на плоскость в виде окружности основания, а на профильную плоскость – в виде эллипса. При этом большая ось эллипса 3˝‑9˝ является проекцией малой оси 3–9 исходного эллипса, а малая ось 0˝‑6˝ представляет собой проекцию большой оси 0–6. На фронтальной плоскости проекция эллипса есть отрезок 0́‑6́, который равен большой оси самого эллипса.
Следовательно, в самом начале построения можно получить две готовые проекции сечения: горизонтальную и фронтальную. После этого нужно построить только профильную проекцию. Следует заметить, что точки 3˝ и 9˝ отделяют видимую часть кривой от невидимой на профильной проекции. Если секущая плоскость Р наклонена к плоскости основания цилиндра под углом 45°, то профильная проекция эллипса является окружностью. На рисунке 105 угол наклона секущей плоскости меньше 45°, вследствие этого профильная проекция большой оси представляет собой малую ось профильной проекции эллипса. В том случае, если бы угол наклона секущей плоскости был больше 45°, проекция большой оси была бы большой осью профильной проекции эллипса.
Построение натурального вида сечения. Сначала нужно отметить цифрами ряд точек на проекциях эллипса (на рис. 105 отмечено 12 таких точек), после чего следует начинать построение натурального вида сечения. Выполнить это можно двумя способами:
1) построением совмещения плоскости Р с горизонтальной плоскостью путем вращения ее около горизонтального следа Ph. На рисунке 105 совмещение построено слева от Ph и соответствующие точки отмечены цифрами с чертой сверху;
2) указанием 12 точек эллипса. При этом хорды, параллельные Ph, проецируются без искажения на горизонтальную плоскость, а расстояния между этими хордами проектируются на фронтальную плоскость. Вследствие этого проводят через точки следа Pv, которые отмечены цифрами, прямые, перпендикулярные Pv. Затем перпендикулярно этим линиям проводят ось симметрии данного эллипса. Вместе с крайними вспомогательными прямыми ее пересечение определит точки эллипса 0 и 6, т. е. концы большой оси. После этого от точек А, В и С следует отложить в обе стороны половины соответствующих хорд (Al = а1, В2 = b2, C3 = с3).
В данном случае хорда 3–9 является малой осью эллипса.
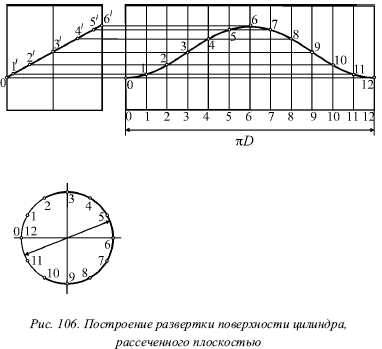
Развертка. На рисунке 106 показано построение развертки боковой поверхности неусеченного цилиндра. Эта боковая поверхность в развернутом состоянии является прямоугольником, основание которого равно длине окружности (πD), а высота – образующей цилиндра.
В данном случае длина окружности заменена периметром вписанного правильного 12‑угольника (рис. 106), после чего через соответствующие точки делений спрямленной окружности проведены образующие. При этом на каждой образующей отмечена ее точка встречи с плоскостью Р.
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: При сдаче лабораторной работы, студент делает вид, что все знает; преподаватель делает вид, что верит ему. 9516 – 

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Сечение цилиндра наклонной плоскостью

************************ –>
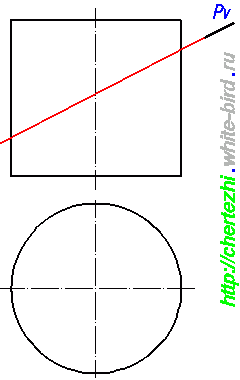
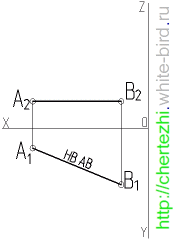
Этим уроком я открываю серию статей, посвященных построению линий пересечения простых тел вращения с наклонной плоскостью. Умение выполнять эти действия вам поможет не только решить одноименные задачи, но и будет серьезным подспорьем при нахождении натурального вида фигуры сечения сложных деталей. Ведь детали состоят из кусочков простых тел: конусов, цилиндров, параллелепипедов, сфер. Сегодня я научу вас строить линию пересечения плоскости с цилиндром. Исходное задание как правило имеет вид как на картинке слева от этого абзаца. Изображены два вида, дающие нам представление о том, что фигура является цилиндром вращения, а так же задается секущая плоскость, в моем случае это плоскость Pv.
Давайте попробуем предположить, что мы получим на каждом из трех видов? Определенно можно сказать, что вся линия пересечения на фронтальном виде сольется с прямой обозначающей секущую плоскость, а на горизонтальном виде, все точки пересечения будут лежать на окружности, которой задан цилиндр. Главный интерес данной задачи заключается в нахождении линии пересечения на третьем виде(на профильной проекции цилиндра). Вероятнее всего вы уже догадываетесь, что на третьем виде линия пересечения будет представлять собой эллипс. В частном случае, если секущая плоскость наклонена к цилиндру вращения под углом ровно 45 градусов, то в проекция сечения на третьем виде будет являться эллипсом с равными осями, т.е. эллипс выродится в окружность. Это был маленький кусочек теории, сейчас же предлагаю перейти к практическим построениям. Итак, перед нами цилиндр с заданной фронтально-проецирующей секущей плоскостью. Начнем с подготовки третьего вида. Он будет точно такой же как и главный вид:
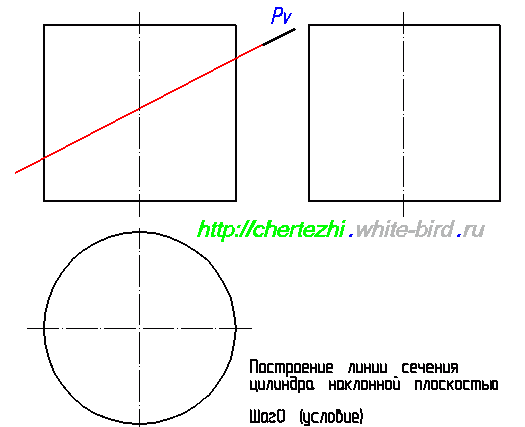
Первым делом давайте обозначим определяющие точки, которые можно найти сразу, без дополнительных построений. Определим точки 1′ и 2′. Горизонтальные проекции 1 и 2 лежат на пересечении образующей окружности с осью, а проекции 1” и 2” лежат на оси цилиндра. Это нужно либо понимать, либо поверить мне 🙂
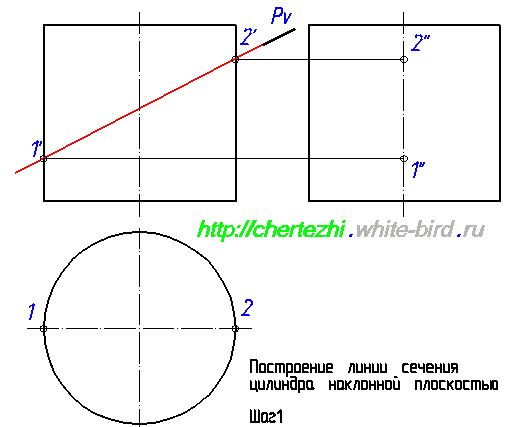
Еще одна пара определяющих точек – точки 3 и 4. Определим их фронтальную проекцию, а потом найдем горизонтальную и профильную. Это не сложно:
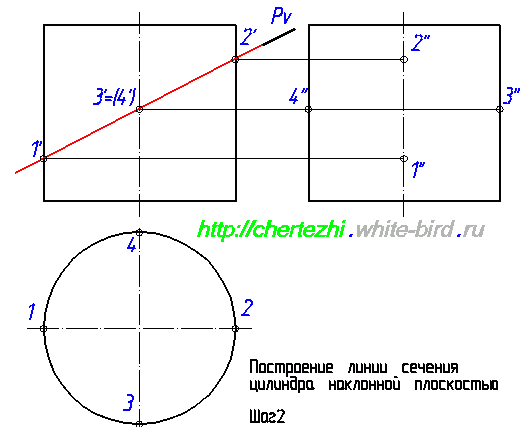
Если бы наша задача была построить сечение в AutoCad, то на этом можно было бы остановиться, поскольку мы уже имеем 4 точки, определяющие оси эллипса. Но так как мы учимся чертить руками, то мы должны построить дополнительные точки, которые бы позволили нам с вами, не обладая точностью компьютера, максимально точно начертить линию пересечения.
Проведем вспомогательную секущую плоскость Q1. На фронтальной проекции в точке пересечения Q1 и Pv отметим точки 5′ и 6′. Снесем их по линии связи на горизонтальную проекцию, отметим там точки 5 и 6:
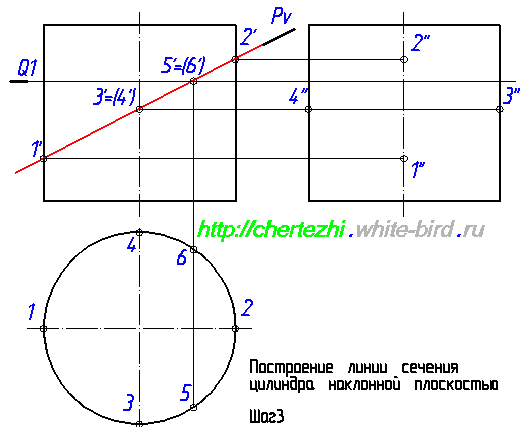
Теперь нужно построить профильные проекции 5” и 6”. Отложим на фронтальной проекции влево от оси точку 6” на расстоянии равном удалению точки 6 от оси окружности на горизонтальной проекции. Эти соответствующие расстояния на рисунке ниже отмечены зелеными отрезками:
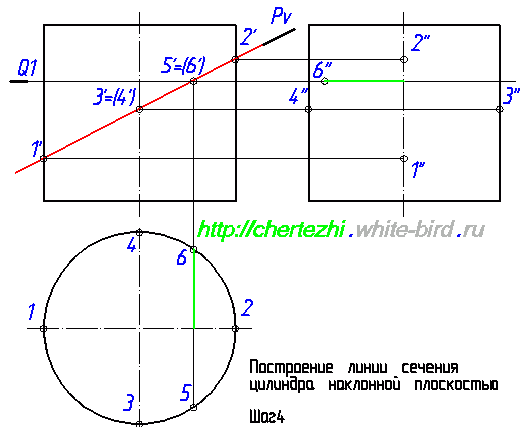
Чтобы построить точку 5” нужно выполнить ровно такие же действия. Нужно отложить аналогичное расстояние вправо от оси цилиндра. Соответствие размеров на профильной и горизонтальной проекции на рисунке ниже обозначено синими отрезками:
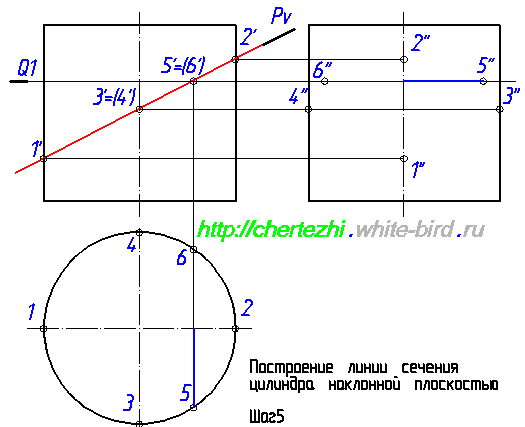
Проведем еще одну вспомогательную секущую плоскость – Q2. Мне нравится проводить вспомогательные плоскости симметрично относительно середины сечения – так во многих случаях удается сделать менее загруженный линиями чертеж. Т.е. я провел Q2 симметрично Q1 относительно точек 3′,4′. Полученные с ее помощью проекции точек 7 и 8 строим по аналогии с построениями проекций точек 5 и 6:
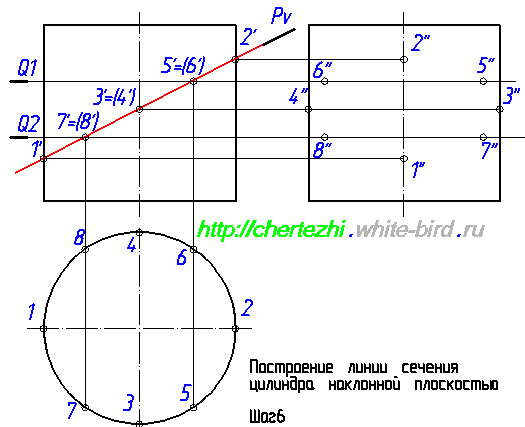
Мы ограничимся построением двух вспомогательных плоскостей и проведем эллипс по имеющимся точкам. Но на практике имеет смысл провести еще хотя бы по одной вспомогательной плоскости выше и ниже точки пересечения Pv с осью цилиндра. Особенно если вы не считаете себя мастером построения эллипса «от руки». Итак, завершающий этап: построение линии пересечения плоскости с цилиндром. Она имеет форму эллипса, строим его аккуратно соединяя точки. И последний штрих – на профильной проекции верхняя половина линии пересечения будет проходить за цилиндром, соответственно будет невидима. Что мы и обозначим штриховой линией.
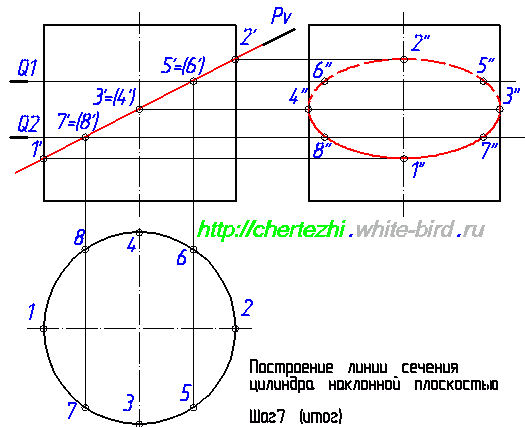
В следующем уроке мы рассмотрим один из случаев построения линии пересечения конуса с плоскостью.
Вы можете сказать «спасибо!» автору статьи:
пройдите по любой из рекламных ссылок в левой колонке, этим вы поддержите проект «White Bird. Чертежи Студентам»
или запишите наш телефон и расскажите о нас своим друзьям – кто-то наверняка ищет способ выполнить чертежи
или создайте у себя на страничке или в блоге заметку про наши уроки – и кто-то еще сможет освоить черчение.
А вот это – не реклама. Это напоминание, что каждый из нас может сделать. Если хотите – это просьба. Мы действительно им нужны: 
Автор комментария: ирина
Дата: 2012-05-29
Автор комментария: Михаил
Дата: 2012-05-30
Мне нужно вырезать эллипс в крыше для вывода металлической трубы, поэтому мне важнее начертить проекцию цилиндра на самой крыше. Спасибо.
Михаил! Ваша задача сводится к продолжению задачи о сечении цилиндра плоскостью. Необходимо найти натуральную величину получившегося сечения. Имея его на руках – распечатываем на формате соответствующего размера, вырезаем трафарет и накладываем в нужном месте на крышу. Останется обвести и произвести вырезание по полученной линии. На сайте есть урок, связанный с нахождением натуральной величины сечений, но там не разобрано построение сечений циллиндрических поверхностей. Ну а в целом – спасибо за доброе слово!
Автор комментария: sakha
Дата: 2012-08-01
Вопрос к практическому применению, понятно как изготовить шаблон верхней проекции сечения, но мне, как сварщику, непонятно как изготовить шаблон для торцовки труб. Объясните, пожалуйста. Спасибо.
Сергей, попробую предложить вам способ. Сразу оговорюсь, что вряд ли он наиболее удобный, но зато качество разметки должно получиться хорошим. Метод потребует выполнить построение развертки цилиндра с нанесением на него линии пересечения с плоскостью. Т.е. я предлагаю вам на чем либо (рубероид, упаковочная бумага, лист обоев и т.д.) построить развертку цилиндра, нанести на нее линию пересечения цилиндра с наклонной плоскостью, отрезать лишнюю часть и, приложив ее к трубе, обвести по краю. Получиться должно просто замечательно.
Думаю, идею вы поняли. Ну а реализация построения линии пересечения на развертке цилиндра – либо найдете, либо дождетесь – планирую написать соответствующую статью.
Всего наилучшего!
Автор комментария: Игорь
Дата: 2012-10-09
Автор комментария:
Дата: 2013-12-17
Автор комментария: препод по ИГ
Дата: 2014-12-14
линия пунктир(пункт по немецки точка)не показывает невидимую линию. Линия невидимого контура называется штриховая. ГОСТ 2.303
Вот! Всегда есть шанс, что кто-то не поленится найти неточность и поправит! Спасибо за замечание, исправляю!
Автор комментария: Надежда
Дата: 2016-01-09
Автор комментария: дмитрий
Дата: 2016-04-18
Спасибо, это понятно по начерт.геометрии, но хотелось бы сделать построение математическим путём, т.к. шаблон, плаз, очень большой. Если дадите буду благодарен.
Автор комментария: vlad
Дата: 2016-04-25
спасибо огромноое очень помогло вспомнил
Автор комментария: Злой Енот
Дата: 2016-09-29
Извиняюсь, Вы нарисовали бред, попробуйте построить по Вашему методу сечение цилиндра плоскостью с наклоном 45 и получите круг, а не эллипс ))))
Приветствую Злого Енота! 🙂 Зачем строить? Это и так известно, будет круг. У меня написано: эллипс с равными осями. Частный случай. Эллипс выродится в круг. Возможно, нужно было прочитать еще пару строк? Или попробовать построить эллипс с равными осями?
Автор комментария: Борис
Дата: 2017-09-17
спасибо очень пригодилось!
Автор комментария: Никита
Дата: 2017-10-29
Здравствуйте! Подскажите как выполните такое же задание при условии что цилиндр проецируется в виде круга на профильную плоскость? Зарание спасибо.
Добавьте свой комментарий:
zakaz@triv >Наша страница в ВК:
Я пока только начал с вами работать, но первые две работы сдал без проблем – сопряжения и построение видов и разрезов. Думаю и дальше все будет ровно. Во всяком случае, вы производите впечатление профессионала в своем деле.
Диаметр основания цилиндра равен 8, а длина его образующей – 
На первый взгляд – задача простая. Кажется, что сечение – трапеция, нижнее ее основание – диаметр цилиндра, найти длину верхнего основания вполне можно, также возможно отыскать высоту трапеции и – дело в шляпе. Однако..
Однако надо помнить, что сечение цилиндра наклонной плоскостью – всегда эллипс или его часть!
Посмотрим на различные сечения цилиндра плоскостями:
Наш случай приблизительно такой:
Сечение цилиндра неосевой плоскостью
И еще нам потребуется знать, какой будет проекция этого сечения на основание цилиндра:
Проекция – вид сверху
Все дело в том, что рассчитать непосредственно площадь сечения трудно из-за сложности его формы, поэтому воспользуемся тем, что
Площадь проекции плоской фигуры равна произведению площади этой фигуры на косинус угла между плоскостью фигуры и плоскостью проекции.
Проекция – вид сверху
Определить площадь проекции будет несложно, давайте это сделаем. Проекция будет представлять собой часть полукруга, которую можно разбить на два круговых сектора и треугольник. Нам известно, что длины дуг относятся как 1:2, значит, меньшая дуга имеет градусную меру 



Площадь треугольника FDC равна половине произведения основания на высоту:
Кроме треугольника FDC в состав площади проекции сечения входят еще два круговых сектора, центральные углы которых равны 30


Осталось определить 
Найдем высоту сечения, это гипотенуза треугольника KGO, KO: 

Косинус нужного угла – отношение прилежащего катета к длине гипотенузы:
Осевое сечение цилиндра прямого и наклонного. Формулы для площади сечения и его диагоналей
Цилиндр — это симметричная пространственная фигура, свойства которой рассматривают в старших классах школы в курсе стереометрии. Для его описания используют такие линейные характеристики, как высота и радиус основания. В данной статье рассмотрим вопросы касательно того, что такое осевое сечение цилиндра, и как рассчитать его параметры через основные линейные характеристики фигуры.
Геометрическая фигура
Сначала дадим определение фигуре, о которой пойдет речь в статье. Цилиндр представляет собой поверхность, образованную параллельным перемещением отрезка фиксированной длины вдоль некоторой кривой. Главным условием этого перемещения является то, что отрезок плоскости кривой принадлежать не должен.

На рисунке ниже показан цилиндр, кривая (направляющая) которого является эллипсом.
Здесь отрезок длиной h является его образующей и высотой.
Видно, что цилиндр состоит из двух одинаковых оснований (эллипсы в данном случае), которые лежат в параллельных плоскостях, и боковой поверхности. Последней принадлежат все точки образующих линий.
Прямой и наклонный цилиндры
Перед тем как переходить к рассмотрению осевого сечения цилиндров, расскажем, какие типы этих фигур бывают.
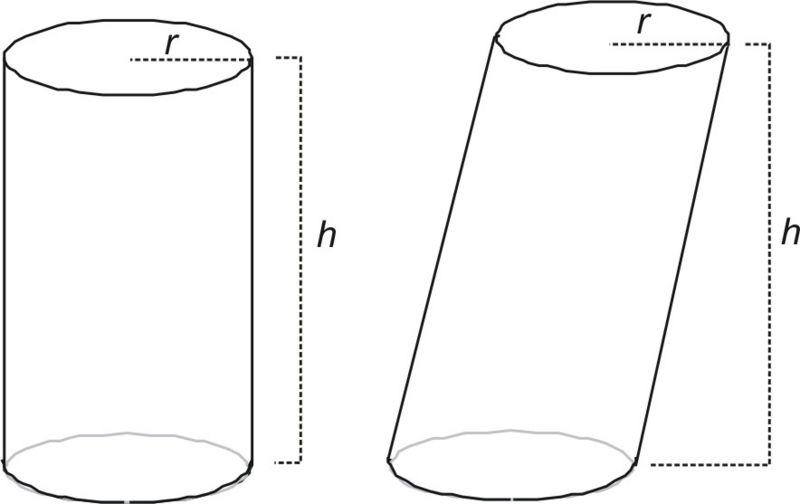
Если образующая линия перпендикулярна основаниям фигуры, тогда говорят о прямом цилиндре. В противном случае цилиндр будет наклонным. Если соединить центральные точки двух оснований, то полученная прямая называется осью фигуры. Приведенный рисунок демонстрирует разницу между прямым и наклонным цилиндрами.
Видно, что для прямой фигуры длина образующего отрезка совпадает со значением высоты h. Для наклонного цилиндра высота, то есть расстояние между основаниями, всегда меньше длины образующей линии.
Далее охарактеризуем осевые сечения обоих типов цилиндров. При этом будем рассматривать фигуры, основаниями которых является круг.
Осевое сечение прямого цилиндра
Осевым называется любое сечение цилиндра, которое содержит его ось. Это определение означает, что осевое сечение будет всегда параллельно образующей линии.
В цилиндре прямом ось проходит через центр круга и перпендикулярна его плоскости. Это означает, что рассматриваемое сечение круг будет пересекать по его диаметру. На рисунке показана половинка цилиндра, которая получилась в результате пересечения фигуры плоскостью, проходящей через ось.
Не сложно понять, что осевое сечение прямого круглого цилиндра представляет собой прямоугольник. Его сторонами являются диаметр d основания и высота h фигуры.
Запишем формулы для площади осевого сечения цилиндра и длины hd его диагонали:
Прямоугольник имеет две диагонали, но обе они равны друг другу. Если известен радиус основания, то не сложно переписать эти формулы через него, учитывая, что он в два раза меньше диаметра.
Осевое сечение наклонного цилиндра
Рисунок выше демонстрирует наклонный цилиндр, изготовленный из бумаги. Если выполнить его осевое сечение, то получится уже не прямоугольник, а параллелограмм. Его стороны — это известные величины. Одна из них, как и в случае сечения прямого цилиндра, равна диаметру d основания, другая же — длина образующего отрезка. Обозначим ее b.
Для однозначного определения параметров параллелограмма недостаточно знать его длины сторон. Необходим еще угол между ними. Предположим, что острый угол между направляющей и основанием равен α. Он же и будет углом между сторонами параллелограмма. Тогда формулу для площади осевого сечения наклонного цилиндра можно записать следующим образом:
Диагонали осевого сечения цилиндра наклонного рассчитать несколько сложнее. Параллелограмм имеет две диагонали разной длины. Приведем без вывода выражения, позволяющие рассчитывать диагонали параллелограмма по известным сторонам и острому углу между ними:
l1 = √(d2 + b2 — 2*b*d*cos(α));
l2 = √(d2 + b2 + 2*b*d*cos(α))
Здесь l1 и l2 — длины малой и большой диагоналей соответственно. Эти формулы можно получить самостоятельно, если рассмотреть каждую диагональ как вектор, введя прямоугольную систему координат на плоскости.
Задача с прямым цилиндром
Покажем, как использовать полученные знания для решения следующей задачи. Пусть дан круглый прямой цилиндр. Известно, что осевое сечение цилиндра — квадрат. Чему равна площадь этого сечения, если площадь поверхности всей фигуры составляет 100 см2?
Для вычисления искомой площади необходимо найти либо радиус, либо диаметр основания цилиндра. Для этого воспользуемся формулой для общей площади Sf фигуры:
Поскольку сечение осевое представляет собой квадрат, то это означает, что радиус r основания в два раза меньше высоты h. Учитывая это, можно переписать равенство выше в виде:
Sf = 2*pi*r*(r + 2*r) = 6*pi*r2
Теперь можно выразить радиус r, имеем:
Поскольку сторона квадратного сечения равна диаметру основания фигуры, то для вычисления его площади S будет справедлива следующая формула:
S = (2*r)2 = 4*r2 = 2*Sf / (3*pi)
Мы видим, что искомая площадь однозначно определяется площадью поверхности цилиндра. Подставляя данные в равенство, приходим к ответу: S = 21,23 см2.
Сечения цилиндра и тригонометрические функции
Разнимем две половинки. Рисунок:
Развернув боковую поверхность, можно заметить, что разрез края будет образовать синусоиду. Рисунок:
Выясним, почему так происходит. Для этого построим математическую модель.
Представим себе прямоугольник с нарисованными на нем осями координат, параллельными соответствующим сторонам прямоугольника. Рисунок:
Свернем этот прямоугольник в прямой круговой цилиндр, радиус основания которого равен 1. Рисунок:
наконец, развернув боковую поверхность. При этом ось Ох свернется в окружность, а ось Оу станет образующей цилиндра . Через диаметр ОО1 полученной окружности проведем сечение плоскостью, составляющей с плоскостью окружности угол 450 . Это сечение является эллипсом.
Возьмем какую-нибудь точку А на эллипсе и опустим из нее перпендикуляры на плоскость окружности и выбранный диаметр. Соответствующие точки пересечения В и С. Рисунок:
Треугольник АВС прямоугольный и равнобедренный, так как > С=450. Следовательно, АВ=ВС
Заметим, что длина ВС равна sinx, где x — длина дуги ОВ окружности. Длина отрезка АВ также равна sinx.
Развернем цилиндр обратно в прямоугольник. При этом эллипс перейдет в кривую, для которой АВ=sinx, где х=ОВ, т.е. эта кривая является частью синусоиды. Рисунок:
Цилиндры
Основные определения и свойства цилиндра
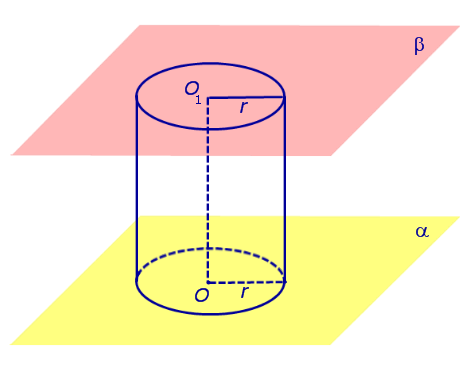
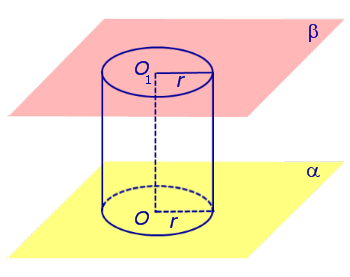
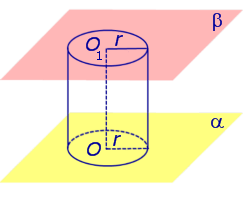
Если из каждой точки окружности опустить перпендикуляр на плоскость β , то основания этих перпендикуляров образуют на плоскости β окружность радиуса r , центр O1 которой является основанием перпендикуляра, опущенного из точки O на плоскость β (рис.2).
Отрезок перпендикуляра, опущенного из любой точки окружности с центром O на плоскость β , который заключен между плоскостями α и β , называют образующей цилиндра .
Совокупность всех образующих цилиндра называют цилиндрической поверхностью .
Фигуру, ограниченную цилиндрической поверхностью и плоскостями α и β, называют цилиндром .
Отрезок OO1 называют осью цилиндра .
Радиус окружности Радиус окружности на плоскости α с центром в точке O называют радиусом цилиндра .
Круги с центрами O и O1 на плоскостях α и β , называют основаниями цилиндра .
Замечание 1. Цилиндрическую поверхность часто называют боковой поверхностью цилиндра . Боковая поверхность цилиндра и основания цилиндра вместе составляют полную поверхность цилиндра .
Замечание 2. Каждая образующая цилиндра параллельна оси цилиндра, а длина каждой образующей цилиндра равна высоте цилиндра.
Замечание 3. Прямая OO1 является осью симметрии цилиндра, а середина отрезка OO1 является центром симметрии цилиндра.
Сечения цилиндра
Определение 2. Сечением цилиндра называют пересечение цилиндра с плоскостью.
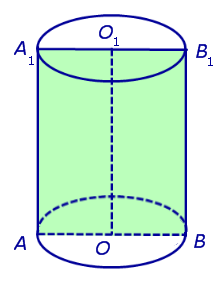
Если сечение проходит через ось цилиндра, то такое сечение называют осевым сечением цилиндра (рис. 3).
На рисунке 3 изображено одно из осевых сечений цилиндра – прямоугольник AA1B1B .
Замечание 4. Каждое осевое сечение цилиндра с радиусом r и высотой h является прямоугольником со сторонами 2r и h .
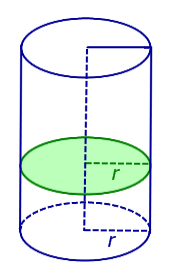
Определение 3. Перпендикулярным сечением цилиндра называют сечение, перпендикулярное оси цилиндра (рис. 4).
Замечание 5. Любым перпендикулярным сечением цилиндра будет круг радиуса r .
Замечание 6. Более подробно случаи взаимного расположения цилиндра и плоскости рассматриваются в разделе нашего справочника «Взаимное расположение цилиндра и плоскости в пространстве».
Объем цилиндра. Площадь боковой поверхности цилиндра.
Площадь полной поверхности цилиндра
Для цилиндра с радиусом r и высотой h (рис. 5)
введем следующие обозначения
| V | объем цилиндра |
| Sбок | площадь боковой поверхности цилиндра |
| Sполн | площадь полной поверхности цилиндра |
| Sосн | площадь основания цилиндра |
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности цилиндра:
при помощи предельного перехода, когда число сторон правильной призмы n неограниченно возрастает. Однако доказательство этого факта выходит за рамки школьной программы.
http://gym1517.narod.ru/awg/swaz.htm
http://www.resolventa.ru/uslugi/uslugischoollosi.htm
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
- Определение цилиндра
- Основные элементы цилиндра
- Виды сечений цилиндра
- Виды цилиндров
Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
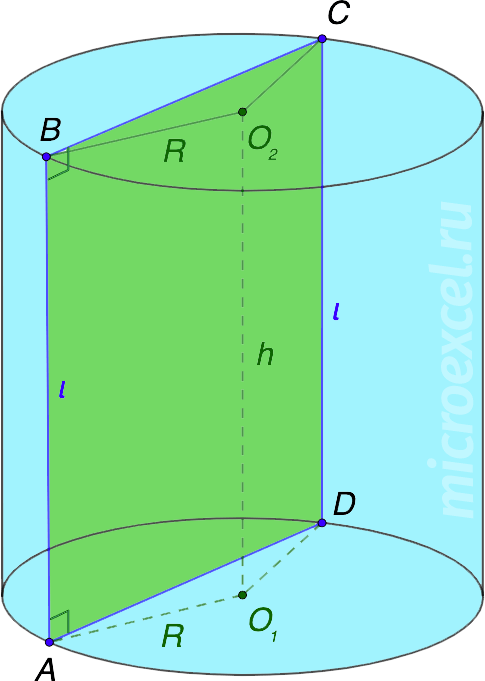
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Основные элементы цилиндра
- Основания цилиндра – два одинаковых по размеру/площади круга с центрами в точках O1 и O2.
- R – радиус оснований цилиндра, отрезки AD и BC – диаметры (d).
- O1O2 – ось симметрии цилиндра, одновременно является его высотой (h).
- l (AB, CD) – образующие цилиндра и одновременно с этим стороны прямоугольника ABCD. Равны высоте фигуры.
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
- длина данного прямоугольника равна длине окружности основания цилиндра (2πR);
- ширина равна высоте/образующей цилиндра.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Виды сечений цилиндра
- Осевое сечение цилиндра – прямоугольник, образованный в результате пересечения фигуры плоскостью, проходящей через ее ось. В нашем случае – это ABCD (см. первый рисунок публикации). Площадь такого сечения равна произведению высоты цилиндра на диаметр его основания.
- Если секущая плоскость проходит не по оси цилиндра, но при этом перпендикулярна его основаниям, то сечением, также, является прямоугольник.
- Если секущая плоскость параллельна основаниям фигуры, то сечение – это идентичный основаниям круг.
- Если цилиндр пересекается плоскостью, не параллельной его основаниям и, при этом, не касающейся ни одной из них, то сечением является эллипс.
- Если секущая плоскость пересекает одно из оснований цилиндра, сечением будет парабола/гипербола.
Виды цилиндров
- Прямой цилиндр – имеет одинаковые симметричные основания (круг или эллипс), параллельные друг другу. Отрезок между точками симметрии оснований перпендикулярен им, является осью симметрии и высотой фигуры.
- Наклонный цилиндр – имеет одинаковые симметричные и параллельные друг другу основания. Но отрезок между точками симметрии не перпендикулярен этим основаниям.
- Косой (скошенный) цилиндр – основания фигуры не взаимно параллельны.
- Круговой цилиндр – основаниями является круг. Также выделяют эллиптические, параболические и гиперболические цилиндры.
- Равносторонний цилиндр – прямой круговой цилиндр, диаметр основания которого равен его высоте.
§ 17. Цилиндр
17.1. Определение цилиндра и его элементов
Определение. Тело, которое образуется при вращении прямоугольника вокруг прямой, содержащей его сторону, называется цилиндром (рис. 141).
Круги, образованные вращением сторон прямоугольника, перпендикулярных оси вращения, называются основаниями цилиндра (верхним и нижним). Так как противоположные стороны прямоугольника равны, то основаниями цилиндра являются равные круги.
Рис. 141
Поверхность, образованная вращением стороны прямоугольника, параллельной оси вращения, называется боковой поверхностью цилиндра, а её площадь — площадью боковой поверхности цилиндра и обозначается Sбок. Объединение боковой поверхности цилиндра и двух его оснований называется полной поверхностью цилиндра, а её площадь обозначается Sполн. Таким образом,
Sполн = Sбок + 2Sосн.(1)
Высотой цилиндра называется перпендикуляр, проведённый из какой-либо точки одного основания цилиндра к плоскости другого. Длину этого перпендикуляра также называют высотой цилиндра. Отрезок, соединяющий точки окружностей оснований и перпендикулярный к их плоскостям, называется образующей цилиндра вращения. Отрезок оси вращения, заключённый внутри цилиндра, называется осью цилиндра.

Если основания прямого кругового цилиндра подвергнуть сжатию так, чтобы окружность основания преобразовалась в эллипс, то получим цилиндр, который называется эллиптическим цилиндром (рис. 142, б).
Так как окружность при параллельном проектировании изображается эллипсом, то изображения кругового и эллиптического цилиндров совпадают.
Цилиндр, образующие которого не перпендикулярны плоскостям его оснований, называется наклонным цилиндром (рис. 142, в).
Рис. 142
Рис. 143
Нам предстоит изучать лишь прямой круговой цилиндр, поэтому слова «прямой круговой» опускаем.
Поверхность, образованную вращением прямой, параллельной оси вращения, называют цилиндрической поверхностью вращения (рис. 143).
Уравнение x2 + y2 = r2 (r > 0) задаёт цилиндрическую поверхность вращения с осью вращения Oz и радиусом основания r. Из этого уравнения следует, что цилиндрическая поверхность является поверхностью второго порядка. (Подробнее о поверхностях второго порядка можно прочитать в «Дополнениях» в конце этой книги.)
17.2. Свойства цилиндра
а) Сечения цилиндра плоскостью. Так как цилиндр является телом вращения, то любое его перпендикулярное сечение есть круг, а перпендикулярное сечение боковой поверхности цилиндра — окружность; центры этих окружностей и кругов — точки пересечения секущих плоскостей и оси цилиндра (рис. 144).
Рис. 144
Рис. 145
Рис. 146
Рис. 147
Рис. 148
Если секущая плоскость пересекает ось цилиндра и не перпендикулярна ей, то в сечении может получиться эллипс (рис. 145) или его некоторая часть (рис. 146, 147). Это следует из того, что параллельной проекцией окружности на плоскость, не параллельную плоскости окружности, является эллипс. (Вспомните: наклонив цилиндрический стеклянный сосуд с водой, вы видите на поверхности воды эллипс или его часть.)
Сечение цилиндра плоскостью, проходящей через ось, называется осевым сечением цилиндра. Так как поворот пространства вокруг прямой на угол 180° является осевой симметрией относительно оси вращения, то ось прямого кругового цилиндра является его осью симметрии. Значит, осевым сечением цилиндра вращения является прямоугольник, стороны которого равны диаметру основания и образующей цилиндра (рис. 148). При этом все осевые сечения цилиндра — равные между собой прямоугольники.
Цилиндр, осевое сечение которого — квадрат, называют равносторонним цилиндром (рис. 149).
Так как все образующие цилиндра равны и параллельны друг другу, то любое сечение цилиндра плоскостью, параллельной его оси, есть прямоугольник, высота которого равна образующей цилиндра (рис. 150).
б) Изображение цилиндра. Чтобы построить изображение цилиндра, достаточно построить: 1) прямоугольник AВB1A1 и его ось OO1 (рис. 151); 2) два равных эллипса, центрами которых являются точки O и O1 и осями — отрезки АВ и A1В1. Выделив штрихами невидимые линии, получаем искомое изображение цилиндра.
Рис. 149
Рис. 150
Рис. 151
в) Касательная плоскость к цилиндру.
Определение. Плоскость, проходящая через образующую цилиндра перпендикулярно плоскости осевого сечения, проведённой через эту образующую, называется касательной плоскостью к цилиндру (рис. 152).
Рис. 152
Говорят, что плоскость α касается цилиндра (цилиндрической поверхности) по образующей DD1, каждая точка образующей DD1 является точкой касания плоскости α и данного цилиндра.
Через любую точку боковой поверхности цилиндра проходит только одна его образующая. Через эту образующую можно провести только одно осевое сечение и только одну плоскость, перпендикулярную плоскости этого осевого сечения. Следовательно, через каждую точку боковой поверхности цилиндра можно провести лишь одну плоскость, касательную к данному цилиндру в этой точке.
17.3. Развёртка и площадь поверхности цилиндра
Следует заметить, что развёртка поверхности вращения — понятие в определённой мере интуитивное. К тому же не для каждой поверхности тела вращения можно построить её развёртку. Иными словами, не каждую поверхность можно «развернуть» на плоскости. Например, не существует развёртки сферы (см. раздел «Дифференциальная геометрия» в конце этой книги).
Рис. 153
Развёртку цилиндра мы также введём на интуитивном уровне.
Пусть R — радиус основания, h — высота цилиндра.
Рис. 154
Рис. 155
Полная поверхность цилиндра состоит из его боковой поверхности и двух оснований — равных кругов. Если эту поверхность «разрезать» по образующей DD1 (рис. 153) и по окружностям оснований, затем боковую поверхность развернуть на плоскости, то получим развёртку полной поверхности цилиндра (рис. 154), состоящую из прямоугольника и двух равных кругов, касающихся противоположных сторон этого прямоугольника (рис. 155).
Попробуйте изготовить развёртку цилиндра и склеить из неё цилиндр.
За площадь боковой поверхности цилиндра принимается площадь её развёртки, т. е. площадь боковой поверхности цилиндра равна площади прямоугольника, у которого одна сторона равна длине окружности основания цилиндра, а другая сторона — высоте цилиндра:
Sбок = 2πRh.
Таким образом, доказана следующая теорема.
Теорема 26. Площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту. ▼
Площадь круга радиуса R равна πR2, поэтому Sосн = πR2. Тогда для нахождения площади полной поверхность цилиндра справедливо:
Sполн = Sбок + 2Sосн = 2πRh + 2πR2 = 2πR(R + h).
Следствие. Пусть цилиндр образован вращением прямоугольника ABCD вокруг его высоты AD (рис. 156). Тогда
Sбок = 2πDC•BC. (1)
Рис. 156
Если EF — серединный перпендикуляр к образующей BC, проведённый из точки F оси l цилиндра, то EF = CD. Учитывая, что ВС = AD, получаем: Sбок = 2πEF•AD, т. е. боковая поверхность цилиндра равна произведению высоты цилиндра на длину окружности, радиус которой равен длине серединного перпендикуляра его образующей, проведённого из точки оcu цилиндра.
Это следствие найдёт своё применение в п. 19.7.
17.4. Призмы, вписанные в цилиндр и описанные около цилиндра
Нам предстоит решать задачи, в которых рассматриваются многогранники, вписанные в фигуры вращения и описанные около них.
Для правильного и наглядного изображения конфигураций из таких многогранников и фигур вращения необходимо верно изображать правильные многоугольники, вписанные в окружность (круг) или описанные около неё.
Определение. Призма называется вписанной в цилиндр, если основания призмы вписаны в основания цилиндра (рис. 157).
Рис. 157
Цилиндр в этом случае называют описанным около призмы.
Боковые рёбра призмы соединяют соответственные вершины её оснований, вписанных в основания цилиндра. Эти вершины лежат на окружностях оснований цилиндра. Образующие цилиндра соединяют соответственные точки окружностей его оснований и параллельны боковым рёбрам призмы. Следовательно, боковые рёбра вписанной в цилиндр призмы — образующие цилиндра.
Определение. Призма называется описанной около цилиндра, если основания призмы описаны около оснований цилиндра.
Рис. 158
Цилиндр при этом называют вписанным в призму (рис. 158).
Так как соответственные стороны оснований призмы параллельны друг другу и перпендикулярны радиусам оснований цилиндра, проведённым в точки касания, то плоскости боковых граней призмы являются касательными плоскостями к цилиндру: эти плоскости касаются поверхности цилиндра по образующим, соединяющим точки, в которых стороны оснований призмы касаются окружностей оснований цилиндра.
При изображении правильных призм, вписанных в цилиндр, следует руководствоваться алгоритмами построений изображений правильных многоугольников, вписанных в окружность.
Итак, для построения изображения правильной призмы, вписанной в цилиндр: 1) строим изображение цилиндра; 2) строим изображение правильного многоугольника, вписанного в верхнее основание цилиндра; 3) через вершины построенного вписанного многоугольника проводим образующие цилиндра; 4) в нижнем основании цилиндра последовательно соединяем концы этих образующих; 5) выделяем видимые и невидимые линии (отрезки) изображаемых фигур.
Рис. 159
На рисунке 159 изображены вписанные в цилиндр: призма, в основании которой прямоугольный треугольник (рис. 159, а); правильная четырёхугольная призма (рис. 159, б); правильная треугольная призма (рис. 159, в); правильная шестиугольная призма (рис. 159, г).
ЗАДАЧА (3.029). Диагональ осевого сечения равностороннего цилиндра равна a
Рис. 160
Решение. Рассмотрим случай а). Пусть в равносторонний цилиндр вписана правильная призма ABCA1B1C1 (рис. 160); CDD1C1 — осевое сечение; OO1 = h — высота цилиндра; ОС = R — радиус основания цилиндра.
Так как цилиндр — равносторонний, то CDD1C1 — квадрат, значит, высота цилиндра равна диаметру его основания. Тогда в квадрате СDD1С1 находим CD = 
Далее, △ АВС — правильный, вписанный в основание, радиус которого R = 





Sосн = 

S
бок = 3SABB1A1 = 3AB•BB1 = 3•

Тогда
Sполн = Sбок + 2Sосн = 


Ответ: a) 

Рис. 161
ЗАДАЧА (3.032). В равносторонний цилиндр, высота которого равна a, вписана правильная призма. Найти расстояние и угол между диагональю боковой грани призмы и осью цилиндра, если призма: а) треугольная; б) четырёхугольная; в) шестиугольная.
Решение. Рассмотрим случай б). Пусть ABCDA1B1C1D1 — вписанная в цилиндр правильная призма (рис. 161). Найдём расстояние и угол между осью OO1 цилиндра и скрещивающейся с ней (почему?) диагональю АB1 боковой грани ABB1A1 данной призмы.
Расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, проведёнными через эти прямые.
Если точка Е — середина отрезка AD, то расстояние между скрещивающимися прямыми AB1 и OO1 равно расстоянию между плоскостью грани ABB1A1 и параллельной ей (почему?) плоскостью сечения EFF1E1. Это расстояние равно длине отрезка ОK (где точка K — середина АВ), так как OK ⟂ (ABB1) и (ABB1) || (EFF1).
Поскольку данный цилиндр — равносторонний, то BDD1B1 — квадрат со стороной BD = ВВ1 = a. Тогда АВ = 



Обозначим ∠ (OO1; AB1) = ϕ, M = AB1 ∩ A1B. Для нахождения угла ϕ проведём в грани ABB1A1 прямую KK1 || OO1. Тогда ϕ = ∠ (OO1; AB1) = ∠ (KK1; AB1). Так как KK1 || OO1, OO1 ⟂ (ABC), то MK ⟂ AB. Поэтому △ АKМ — прямоугольный. В этом треугольнике АK = 




Ответ: б) 


Действительно, Sбок. пов. призм = h•Pосн. призм, где Росн. призм — периметр основания призмы, h — длина её высоты. Для правильных вписанных в цилиндр призм h — постоянная величина, равная длине высоты цилиндра, а предел последовательности периметров правильных многоугольников, вписанных в окружность (основание цилиндра), равен длине этой окружности. Таким образом, мы вновь получаем: Sбок = 2πRh.
17.5. Объём цилиндра
Напомним принятое нами соглашение, основанное на принципе Кавальери.
«Пусть даны два тела и плоскость. Если каждая плоскость, параллельная данной плоскости и пересекающая одно из данных тел, пересекает также и другое, причём площади сечений, образованных при пересечении обоих тел, относятся как m : n, то и объёмы этих тел относятся как m : n».
Рис. 162
Расположим цилиндр, имеющий высоту h и радиус основания R, и прямоугольный параллелепипед с рёбрами h, R, R так, чтобы их основания находились на двух параллельных плоскостях, расстояние между которыми равно h (рис. 162). Каждая плоскость, параллельная данным плоскостям и пересекающая цилиндр, пересекает также прямоугольный параллелепипед, причём площади образованных при пересечении обоих тел сечений относятся как π•R2 : R2 = π : 1. Тогда и для объёмов этих тел справедливо: Vцил : Vпарал = π : 1 или Vцил : (R2•h) = π : 1, откуда
Vцил = π•R2•h.
Если цилиндр высотой h пересечь плоскостью, параллельной его оси, то этот цилиндр разобьётся на два тела (рис. 163). Объёмы этих тел относятся как площади сегментов, образовавшихся в основании цилиндра (докажите это на основании принципа Кавальери). Следовательно, объём каждого из этих тел может быть вычислен по формуле
V = Sсегм•h.
Рис. 163
Рис. 164
Любая плоскость, проведённая через середину оси цилиндра, разбивает этот цилиндр на два равновеликих тела (рис. 164), объём V каждого из которых равен половине объёма данного цилиндра, т. е. V = 
Попробуйте, исходя из этой формулы, доказать, что в таком случае объём каждой части цилиндра (см. рис. 164) может быть вычислен по формуле:
V= 
где a и b — длины отрезков, на которые образующая цилиндра делится секущей плоскостью.
Сечение цилиндра: определение, виды, его образующая
Содержание:
- Кратко о цилиндре
- Осевое сечение
- Как найти площадь сечения
- Осевое сечение наклонного цилиндра
-
Примеры задач
- Задача 1
- Задача 2
Кратко о цилиндре
Цилиндр — это геометрическая фигура, которая ограничена цилиндрической поверхностью и двумя плоскими окружностями.
Также можно сказать, что это тело вращения, возникающее при вращении прямоугольника вокруг его стороны.
Осевое сечение
Это сечение фигуры плоскостью, проходящей через ее ось. Оно является прямоугольником. Таким образом, любое сечение, параллельное оси цилиндра (и перпендикулярное его основанию), становится прямоугольником. Сторонами этой фигуры будет диаметр цилиндра и высота его оси.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как найти площадь сечения
Формула 1
(S = d*h,)
где (d) — диаметр, а (h) — высота всей фигуры.
Также есть формулы для расчета площади сечения, параллельного оси геометрического тела (но не пересекающего ее).
Формула 2
(S = a*h, )
где (a) — хорда.
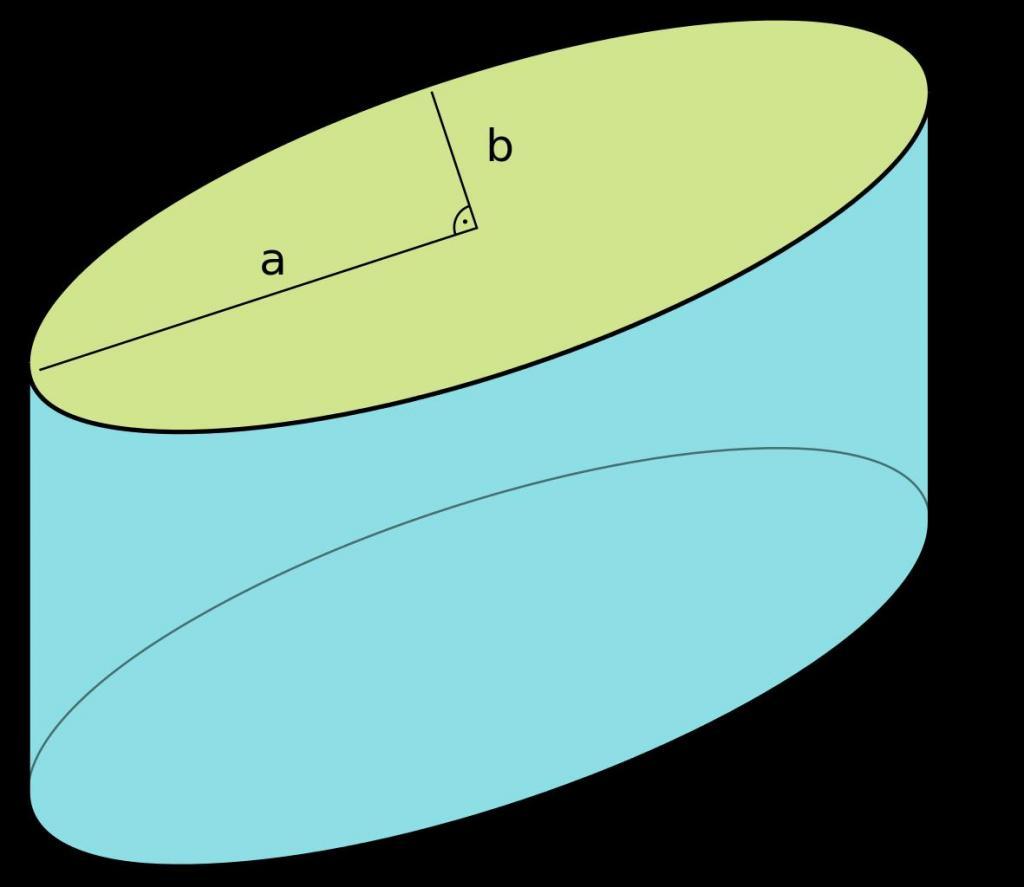
Осевое сечение наклонного цилиндра
Сечение наклонного цилиндра по оси представляет собой параллелограмм. Его стороны нам уже известны: одна из них равна диаметру d, как и в случае с прямой фигурой. Другая — длина образующего отрезка. Ее мы можем обозначить буквой b.
Для точного определения всех параметров параллелограмма недостаточно знать только длины его сторон. Для расчета площади фигуры нам понадобится один из ее углов. Допустим, что острый угол между плоскостью и направляющий равен α. Тогда формула S параллелограмма будет выглядеть следующим образом:
(S = d * b * sin(α))
Примеры задач
Рассмотрим пару задач на осевое сечение с решениями.
Задача 1
Дан круглый прямой цилиндр. Его осевое сечение является квадратом. Вопрос: чему равна S сечения, если площадь поверхности всего цилиндра — 100 см²?
Решение
Чтобы найти S квадрата, нужно сначала определить радиус или диаметр окружности цилиндра. Для этого вспомним формулу для нахождения площади самого цилиндра:
(Sц = 2pi * r * (r + h))
Так как осевое сечение — квадрат, значит радиус основания в два раза меньше высоты фигуры. В таком случае, формула будет выглядеть так:
(Sц = 2pi * r * (r + 2r) = 6 * pi * r²)
Исходя из этого, будем выражать радиус:
(r = √(Sц / (6*pi)))
Если сторона квадратного сечения равна диаметру основания цилиндра, то для определения площади квадрата S используем формулу:
(S = (2*r)2 = 4*r2 = 2*Sц/ (3*pi))
Подставим известные данные ((Sц = 100см^2)) и получим площадь сечения (S = 21,23 см²).
Ответ: (S = 21,23 см²).
Задача 2
Дано: ABCD — осевое сечение цилиндра. Площадь сечения (Sc) равна (10 м²), а площадь основания (Sо— 5 м²). Найти высоту цилиндра.
Решение
Так как площадь основания — круг, то (Sо = pi * r²). Тогда (r = √(Sо/pi) = √(5/pi).)
Так как площадь сечения — прямоугольник, то (Sc = AB * BC = h * 2r.) Тогда (h = Sc/(2r) = 10/(2√(5/pi)) = 5√(pi/5) = √(5pi).)
Ответ: (h = √(5pi).)
Насколько полезной была для вас статья?
Рейтинг: 5.00 (Голосов: 1)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так