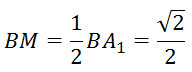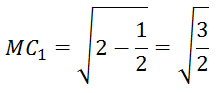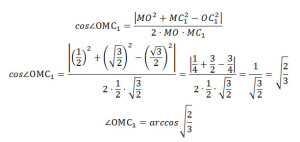Задачи на построение сечений куба плоскостью, как правило, проще чем, например, задачи на сечения пирамиды.
Провести прямую можем через две точки, если они лежат в одной плоскости. При построении сечений куба возможен еще один вариант построения следа секущей плоскости. Поскольку две параллельные плоскости третья плоскость пересекает по параллельным прямым, то, если в одной из граней уже построена прямая, а в другой есть точка, через которую проходит сечение, то можем провести через эту точку прямую, параллельную данной.
Рассмотрим на конкретных примерах, как построить сечения куба плоскостью.
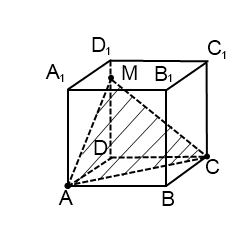
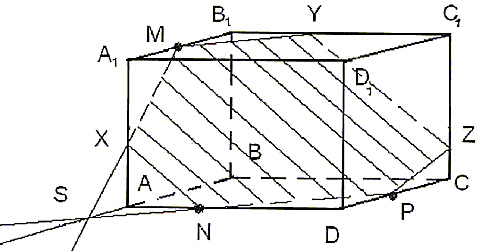
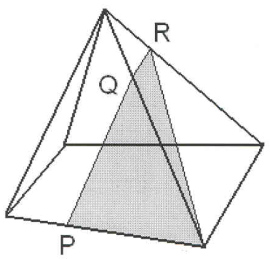
1) Построить сечение куба плоскостью, проходящей через точки A, C и M.
Задачи такого вида — самые простые из всех задач на построение сечений куба. Поскольку точки A и C лежат в одной плоскости (ABC), то через них можем провести прямую. Ее след — отрезок AC. Он невидим, поэтому изображаем AC штрихом. Аналогично соединяем точки M и C, лежащие в одной плоскости (CDD1), и точки A и M, которые лежат в одной плоскости (ADD1). Треугольник ACM — искомое сечение.
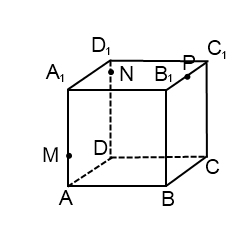
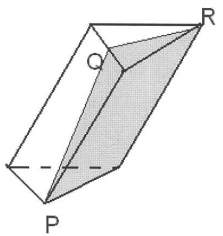
2) Построить сечение куба плоскостью, проходящей через точки M, N, P.
Здесь только точки M и N лежат в одной плоскости (ADD1), поэтому проводим через них прямую и получаем след MN (невидимый). Поскольку противолежащие грани куба лежат в параллельных плоскостях, то секущая плоскость пересекает параллельные плоскости (ADD1) и (BCC1) по параллельным прямым. Одну из параллельных прямых мы уже построили — это MN.
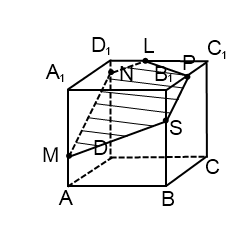
Проводим прямую через точки M и S, лежащие в одной плоскости (ABB1). Получили след MS (видимый).
Плоскости (ABB1) и (CDD1) параллельны. В плоскости (ABB1) уже есть прямая MS, поэтому через точку N в плоскости (CDD1) проводим прямую, параллельную MS. Эта прямая пересекает ребро D1C1 в точке L. Ее след — NL (невидимый). Точки P и L лежат в одной плоскости (A1B1C1), поэтому проводим через них прямую.
Пятиугольник MNLPS — искомое сечение.
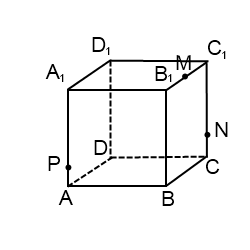
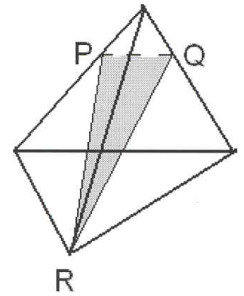
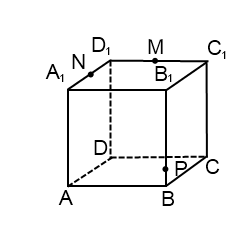
3) Построить сечение куба плоскостью, проходящей через точки M, N, P.
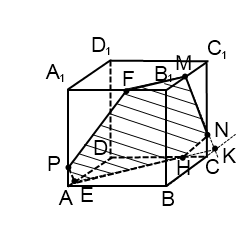
Точки M и N лежат в одной плоскости (ВСС1), поэтому через них можно провести прямую. Получаем след MN (видимый). Плоскость (BCC1) параллельна плоскости (ADD1),поэтому через точку P, лежащую в (ADD1), проводим прямую, параллельную MN. Она пересекает ребро AD в точке E. Получили след PE (невидимый).
Больше нет точек, лежащей в одной плоскости, или прямой и точки в параллельных плоскостях. Поэтому надо продолжить одну из уже имеющихся прямых, чтобы получить дополнительную точку.
Если продолжать прямую MN, то, поскольку она лежит в плоскости (BCC1), нужно искать точку пересечения MN с одной из прямых этой плоскости. С CC1 и B1C1 точки пересечения уже есть — это M и N. Остаются прямые BC и BB1. Продолжим BC и MN до пересечения в точке K. Точка K лежит на прямой BC, значит, она принадлежит плоскости (ABC), поэтому через нее и точку E, лежащую в этой плоскости, можем провести прямую. Она пересекает ребро CD в точке H. EH -ее след (невидимый). Поскольку H и N лежат в одной плоскости (CDD1), через них можно провести прямую. Получаем след HN (невидимый).
Плоскости (ABC) и (A1B1C1) параллельны. В одной из них есть прямая EH, в другой — точка M. Можем провести через M прямую, параллельную EH. Получаем след MF (видимый). Проводим прямую через точки M и F.
Шестиугольник MNHEPF — искомое сечение.
Если бы мы продолжили прямую MN до пересечения с другой прямой плоскости (BCC1), с BB1, то получили бы точку G, принадлежащую плоскости (ABB1). А значит, через G и P можно провести прямую, след которой PF. Далее — проводим прямые через точки, лежащие в параллельных плоскостях, и приходим к тому же результату.
Работа с прямой PE дает то же сечение MNHEPF.
4) Построить сечение куба плоскостью, проходящей через точку M, N, P.
Общеобразовательная школа І-ІІІ ступеней
№2
отдела образования администрации города Кировское
«Сечение куба плоскостью
и практическое их применение
в задачах».
Подготовила учитель математики
учитель-методист
Чумакова Г.В.
2015 г.
Введение:
Задачи
на построение сечений многогранников занимают значительное место как школьном
курсе геометрии для старших классов, так и на экзаменах разного уровня. Решение
этого вида задач способствует усвоению аксиом стереометрии, систематизации
знаний и умений, развитию пространственного представления и конструктивных
навыков. Общеизвестны трудности, возникающие при решении задач на построение
сечений.
Основными
действиями, составляющими метод построения сечений, являются нахождение точки
пересечения прямой с плоскостью, построение линий пересечения двух плоскостей,
построение прямой параллельной плоскости, построение прямой перпендикулярной
плоскости.
Проиллюстрирую
построение сечения на одной задаче из школьного курса математики:
№1.
Постройте хотя бы два сечения куба ABCDA1B1C1D1 плоскостью
АМ1С, если точка М1 движется по отрезку ВВ1 от
В до В1. Найдите границы измерения высоты сечения, проведённой из
точки М1.
Решение:
Построим два требуемых сечения, взяв точку М1 ближе к точке В, а
точку М2 ближе к В1. Оба сечения показаны на рисунке .В
начале движения когда точка М1только отошла от точки В1,
сечение представляет собой треугольник с основанием АС и высотой М1О,
которая чуть больше отрезка ВО, т.е. Если точка
М1 займёт положение М2 расположенной очень близко к точке
В1, то АМ2С
почти совпадёт с АВ1С,
а его высота М1О – с отрезком В1О, длина которого равна (ОВ1=
=
).
Отсюда по
соображениям непрерывности делаем вывод:
Особо следует посмотреть, что произойдёт, если точка М1
займёт положение вершины В.
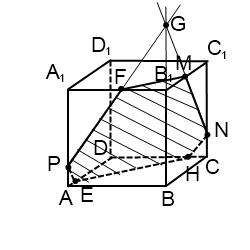
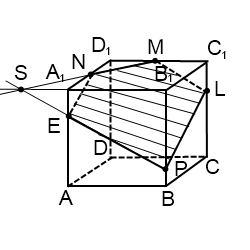
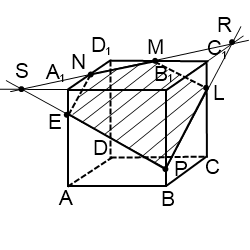
№2.
Построить сечение куба плоскостью, проходящей через три точки А1, E
и L, лежащие на рёбрах куба.
Плоскости
граней A1ADD1 и DD1C1C пересекаются
по прямой DD1, а плоскости
граней A1B1C1D1 u DD1C1C – по прямой D1C1. Соединив
точки А и Е , получим прямую пересечения секущей плоскости с плоскостью грани AA1D1D, а продолжив
её, найдём точку N, принадлежащую
трём плоскостям: плоскости сечения и плоскостям граней AA1D1D u DD1C1C.
Аналогично
найдём точку М, общую трём плоскостям: плоскости сечения и плоскостям граней A1B1C1D1 u DD1C1C. Таким
образом, точки N u M принадлежат
секущей плоскости и плоскости DD1C1C; прямая MN – линия
пересечения плоскости сечения с плоскостью грани DD1C1C, а F и K –
точки пересечения её с рёбрами куба CD u CC1.
Последовательно соединив прямыми точки A1, E, F, K u L, получаем
пятиугольник A!EFKL, который и
даст нам искомое сечение.
При
построении сечения куба плоскостью Х при произвольном расположении точек
в сечении получается: треугольник, трапеция, прямоугольник, пятиугольник или
шестиугольник. Естественно возник вопрос, как вид сечения зависит от вида
расположения точек задающих это сечение
Я решил провести
исследование, цель которого является выяснение.
Построить сечения куба
плоскостью, когда заданы три точки принадлежащие рёбрам с одной вершиной.
Взяты три точки A1, D, C1, которые
принадлежат вершине D1, а сами
являются вершинами куба.
В сечении получился равносторонний
треугольник, так как A1C1, A1D u DC1 – диагонали
граней этого куба.
Три точки: A1 u C1 – вершины
куба, а точка F принадлежит
ребру куба DD1. Точки
принадлежат прямым выходящим из вершины D1.
В сечении получился равнобедренный
треугольник, так как F равноудалена
от точек A1 u C1.
Три точки: A1 u C1 – вершины
куба, а точка F принадлежит
прямой ребра куба DD1. Точки
принадлежат прямым выходящим из одной вершины D1.
В сечении получается равнобедренная
трапеция, так как F равноудалена
от точек A1 u C1, то есть LA1=KC1.
Три точки принадлежащие рёбрам с одной
вершиной D1. Точки F u M принадлежат
продолжениям рёбер D1D u D1C соответственно, а
точка A1 является
вершиной куба.
В сечении получился пятиугольник A1KLNG.
Взяты три точки F, M u Q так, что лежат на
продолжении рёбер D1D, D1C1, и D1A1
соответственно.
В сечении получился шестиугольник KLNGJH.
Три точки лежат на рёбрах с одной
вершиной D1.
В сечении получился произвольный
треугольник, но если точки расположить так чтобы D1Q=D1M=D1F, то есть если они были
бы равноудалены от вершины D1 то в сечении получился бы
равносторонний треугольник.
Секущая плоскость задана точками Н, Q и M. В сечении получается
параллелограмм, так как KC ││ MP и MK ││ PC по теореме о пересечении двух
параллельных плоскостей третьей.
Если точки H, Q и M, задают секущую
плоскость, удаленные от D, на расстоянии
2a, где а – для
ребра куба, то в сечении получается правильный треугольник ACB1.
Вывод: три задающих
сечение точки принадлежат трём рёбрам куба с общей вершиной или являются их
продолжением, то в сечении получается: треугольник, пятиугольник, шестиугольник
трапеция, параллелограмм.
Построение сечения
куба плоскостью, когда заданы три точки, две из которых лежат на смежных
рёбрах, а третья точка лежит на ребре не смежном с ними.
Три точки M, K u F, взяты так что M u F принадлежат рёбрам с одной вершиной A1, а точка K лежит на ребре не
смежным с ними.
В сечении получается
прямоугольник, так как А1М=D1K и по теореме о трёх перпендикулярах
можно доказать что MKLF –
прямоугольник., а если А1МD1K, то может получится
трапеция или пятиугольник.
Взяты три точки так, что K u L принадлежат рёбрам
выходящим из одной вершины A1, а точка N принадлежит ребру CC1, не смежному
сними. K, L u N середины рёбер A1A, A1B1 u CC1 –
соответственно.
В сечении получается правильный
шестиугольник KLGNHM
Взяты три точки так, что K u L принадлежат рёбрам
выходящим из одной вершины A1, а точка T принадлежит ребру DC.
В сечении получается шестиугольник KLFRTZ.
Три точки взяты так, что K u L принадлежат рёбрам
куба с одной вершины A1, а точка M ребре DD1.
В сечении получается трапеция LKQM.
Три точки K u L которые принадлежат рёбрам с одной вершиной A1.и точка R которая лежит на ребре
BC.
В сечении получается пятиугольник KLFRT.
Вывод: Если секущая
плоскость задана тремя точками, две из которых лежат на смежных рёбрах, а
третья на ребре не смежном с ними, то в сечении может получиться прямоугольник,
пятиугольник, шестиугольник, трапеция.
В сечении куба
параллелограмм и его частные случаи.
Точки T, H, J задающие сечение расположены так, что THAD, HJ
AD. В сечении получается
квадрат HTKJ.
Сечение задано точками C, F, L, причём DF=FD1, BL=LB1. В сечении
получается ромб AFCL.
Сечение задано точками C, G, H. B1H=DG. В сечении
параллелограмм A1GCH.
Точки задающие сечение являются
вершинами куба A, D, C1. В сечении
получается прямоугольник
В
сечении куба правильные многоугольники
Треугольник АВВ1 равносторонний,
так как его стороны это диагонали граней куба.
Треугольник КМТ равносторонний, так как
КВ=МВ=ТВ.
КМТЕ – квадрат, так как сечение задано
точками М, К, Е и МКAD, EK
AD.
В сечении правильный шестиугольник
КМТНЕО, так как точки Н, Е, К задающие сечение являются серединами рёбер СС1,
DC, АА1 соответственно.
Куб и несколько задач
по стереометрии с ЕГЭ.
В пособии “ЕГЭ 2005.
Математика. Типовые тестовые задачи” (Корникова Т. А. и др.) Содержит 10 задач
(С4) по стереометрии, объединенных общей идеей: дана треугольная призма АВСА1В1С1
стороны основания АВ и ВС взаимно перпендикулярны и перпендикулярны ребру ВВ1,
АВ=ВС=ВВ1, вершина А является вершиной конуса (или центром одного из
оснований цилиндра, или центром сферы), основание конуса (сфера или второе
основание цилиндра) проходит через середину одного ребра призмы, длина его
известна. Надо найти объем или поверхность конуса (сферы, цилиндра).
Общий пример решения:
Данную призму дополнить
до куба. Шестиугольник DEFKLM – сечение куба
плоскостью основания конуса , окружность которого проходит через середину А1В1,
А – вершина конуса, или
DEFKLM – сечение куба плоскостью основания
цилиндра, окружность которого проходит через середину А1В1,
А – центр второго основания цилиндра, или это сечение куба плоскостью большого
круга сферы с центром А, сфера которого проходит через середину А1В1.
Шестиугольник DEFKLM – сечение куба
плоскостью, проходящей через середину рёбер А1В1, ВВ1,
ВСЖ при построении получаются точки K, L, M, которые
являются серединами соответствующих рёбер. Стороны этого шестиугольника
являются гипотенузами треугольников DB1E, EBF, FCK, KQL, LRM, MA1D, катеты
которых равны половине ребра куба. Тогда центр этого шестиугольника является
центром описанной около него окружности, которая пересекает рёбра куба в точках
D,E, F, K, L и М, радиус
этой окружности , где А1В1=а.
AO EL, т. к.
EAL – равнобедренный: AL=AE.
(ABE u
EAL –
прямоугольные, AB=AQ= а, BE=LQ=)
EO=OL как середина
диагонали ЕL шестиугольника
DEFKLM, т. е. АО –
медиана ,а по свойствам равнобедренного треугольника и высота. Аналогично
доказывается АО DK. Так как АО
перпендикулярна к двум пересекающимся прямым плоскости шестиугольника, то АО
перпендикулярна ко всей плоскости.
Если А –
вершина конуса то АО – его высота, если А – центр второго основания цилиндра,
то АО- высота цилиндра.
АВС:
АС=, P – точки пресечения
диагоналей основания куба, АР=, РР1=АА1= а. ОР=
РР1=
,
тогда из прямоугольного РОА АО=
. И так АО=
.
Тогда, если
идёт речь о конусе:
=
(из
).
Ответ:
Если речь идёт
цилиндре:
Ответ:
Если речь идёт
о сфере:
Ответ:
Корникова Т. А.
и др. типовые тестовые задания. ЕГЭ – 2005
Вариант 6.
Задача.
Даны призма АВСА1В1С1 и цилиндр. Стороны АВ и
ВС основания призмы перпендикулярны ребру ВВ1 и взаимно
перпендикулярны. Центром основания цилиндра служит точка А1
окружность второго основания проходит через середину ребра А1В1.
Найдите площадь
полной поверхности цилиндра, если ВВ1=АВ=ВС=10. Найдите его объём.
Решение:
.
.
Так как стороны
АВ и ВС основания призмы перпендикулярны ребру ВВ1 и взаимно
перпендикулярны и АВ=ВС=ВВ1, то призма АВСА1В1С1
– это половина куба с ребром АВ. Окружность второго основания цилиндра проходит
через середину А1В1. Эта окружность пересекает и другие
рёбра куба. И эти точки пересечения окружности второго основания цилиндра и
рёбер куба лежит в одной плоскости (плоскость сечения) и равноудалены от центра
второго основания цилиндра. Плоскость второго основания цилиндра образует в
сечении куба шестиугольник DEFKLM, все вершины которого
являются вершинами соответствующих рёбер. Тогда ED=АР=R, ЕВ1D,
В=900 (по условию), B1E=DB1=
, тогда по теореме Пифагора ED=
, R=
.
Докажем, что АО
перпендикулярно к сечению DEFKLM,так как является его
высотой цилиндра.
РОА
, Р=900 РА=
, РО=
.
По теореме
Пифагора ОА= (ОА=h=
).
SPO,
P=900 PS=
SO
в AOS:

SO2=
AS2=AO2+SO2. AOS –
прямоугольный АОSO.
Ответ:
Корникова Т. А.
и др. типовые тестовые задания. ЕГЭ – 2005
Вариант 10.
Задача.
Даны призма АВСА1В1С1 и конус. Стороны АВ и ВС
основания перпендикулярны ребру ВВ1 и взаимно перпендикулярны.
Вершина конуса располагается в точке А, окружность основания проходит через
середину ребра А1В1.
Найдите площадь
полной поверхности конуса, если ВВ1=АВ=ВС=8. Найдите объём этого
конуса.
Решение:
.
.
Так как по
условию дана прямая призма, в которой ВВ1=АВ=ВС, то эта призма
является половиной куба. Вершина куба А является и вершиной конуса, основание
которого пересекает А1В1 в точке D, следовательно
AD – образующая
конуса AD=. Сечение куба плоскостью основания конуса
– это правильный шестиугольник DEFKLM, т.к. АD, AE, AF, AK, AL, AM – это
образующие конуса, вершины D, E, F, K, L, M – равноудалены
от основания высоты конуса в точке О, являются серединами рёбер куба. R=ED, EB1D, B1D =B1E=4,
ED=4.
AA1D,
A1=900, AD=
.
.
AC=
(из
ОАН, ОН
АН,
НО=4, АН=4).
Ответ:
3. Заключение.
В результате проведённого компьютерного
эксперимента в работе было выявлено: что в зависимости от точек задающих
секущую плоскость в сечении куба могут получиться треугольники (произвольный,
равнобедренный и правильный), четырёхугольники (квадрат, прямоугольник,
трапеция, ромб, параллелограмм), пятиугольники и шестиугольники. Особое
выделены правильный треугольник и шестиугольник, рассмотрены свойства этих
многоугольников и задачи с ними связанные располагавшиеся в одном из пособий
для подготовки к ЕГЭ по математике.
Выполнение работы расширило мои представления
о выполнении построений сечения многогранников плоскостью, дало возможность
более глубоко освоить некоторые компьютерные программы способствующие развитию
конструктивных навыков, которые позволили разобраться в решении задач по
стереометрии, предлагающихся в ЕГЭ по математике.
Метод сечений многогранников в стереометрии
используется в задачах на построение. В его
основе лежит умение строить сечение
многогранника и определять вид сечения.
Данный материал характеризуется следующим
особенностями:
- Метод сечений применяется только для
многогранников, так как различные сложные
(наклонные) виды сечений тел вращения не входят в
программу средней школы. - В задачах используются в основном простейшие
многогранники. - Задачи представлены в основном без числовых
данных, чтобы создать возможность их
многовариантного использования.
Чтобы решить задачу построения сечения
многогранника ученик должен знать:
- что значит построить сечение многогранника
плоскостью; - как могут располагаться относительно друг
друга многогранник и плоскость; - как задается плоскость;
- когда задача на построение сечения
многогранника плоскостью считается решенной.
Поскольку плоскость определяется:
- тремя точками;
- прямой и точкой;
- двумя параллельными прямыми;
- двумя пересекающимися прямыми,
построение плоскости сечения проходит в
зависимости от задания этой плоскости. Поэтому
все способы построения сечений многогранников
можно разделить на методы.
Существует три основных метода построения
сечений многогранников:
- Метод следов.
- Метод вспомогательных сечений.
- Комбинированный метод.
Первые два метода являются разновидностями Аксиоматического
метода построения сечений.
Можно также выделить следующие методы
построения сечений многогранников:
- построение сечения многогранника плоскостью,
проходящей через заданную точку параллельно
заданной плоскости; - построение сечения, проходящего через заданную
прямую параллельно другой заданной прямой; - построение сечения, проходящего через заданную
точку параллельно двум заданным скрещивающимся
прямым; - построение сечения многогранника плоскостью,
проходящей через заданную прямую
перпендикулярно заданной плоскости; - построение сечения многогранника плоскостью,
проходящей через заданную точку перпендикулярно
заданной прямой.
В федеральный перечень учебников по геометрии
для 10-11 класов входят учебники авторов:
- Атанасяна Л.С., Бутузова В.Ф., Кадомцева С.Б. и др
(Геометрия, 10-11); - Погорелова А.В. (Геометрия, 7-11);
- Александрова А.Д., Вернера А.Л., Рыжик В.И.
(Геометрия, 10-11); - Смирновой И.М. (Геометрия, 10-11);
- Шарыгина И.Ф. (Геометрия, 10-11).
Рассмотрим подробнее учебники Л.С, Атанасяна и
Погорелова А.В.
В учебнике Л.С. Атанасяна на тему “Построение
сечений многогранников” выделено два часа. В 10
классе в теме “Параллельность прямых и
плоскостей” после изучения тетраэдра и
параллелепипеда отводится один час на изложение
параграфа “Задачи на построение сечений”.
Рассматриваются сечения тетраэдра и
параллелепипеда. И тема “Параллельность прямых
и плоскостей” завершается решением задач на
одном или двух часах (всего задач на построение
сечений в учебнике восемь).
В учебнике Погорелова А.В. на построение
сечений отводится около трех часов в главе
“Многогранники”: один – на изучение темы
“Изображение призмы и построение ее сечений”,
второй – на изучение темы “Построение пирамиды
и ее плоских сечений” и третий – на решение
задач. В списке задач, приведенных после темы,
задач на сечение насчитывается всего около
десяти.
Мы предлагаем систему уроков по теме
“Построение сечений многогранников” для
учебника Погорелова А.В.
Материал предлагается расположить в той
последовательности, в какой он может применяться
для обучения учащихся. Из изложения темы
“Многогранники” предлагается исключить
следующие параграфы: “Построение сечений
призмы” и “Построение сечений пирамиды” с тем,
чтобы систематизировать данный материал в конце
этой темы “Многогранники”. Классифицировать
его по тематике задач с примерным соблюдением
принципа “от простого к сложному” можно весьма
условно следующим образом:
- Определение сечения многогранников.
- Построение сечений призмы, параллелепипеда,
пирамиды методом следов. (Как правило в школьном
курсе стереометрии используются задачи на
построение сечений многогранников, решаемые
основными методами. Остальные методы, в связи с
их более высоким уровнем сложности, учитель
может оставить для рассмотрения на
факультативных занятиях или на самостоятельное
изучение. В задачах на построение основными
методами требуется построить плоскость сечения,
проходящую через три точки). - Нахождение площади сечений в многогранниках
(без использования теоремы о площади
ортогональной проекции многоугольника). - Нахождение площади сечений в многогранниках (с
применением теоремы о площади ортогональной
проекции многоугольника).
СТЕРЕОМЕТРИЧЕСКИЕ ЗАДАЧИ НА
ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ И МЕТОДИКА ИХ
ИСПОЛЬЗОВАНИЯ НА УРОКАХ В 10-11 КЛАССАХ.(система уроков и факультативных
занятий по теме “Построение сечений
многогранников”)
УРОК 1.
Тема урока: “Построение сечений
многогранников”.
Цель урока: ознакомление с методами
построений сечений многогранников.
Этапы урока:
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала:
А) Определение сечения.
Б) Методы построений сечений:
а) метод следов;
б) метод вспомогательных сечений;
в) комбинированный метод.
- Закрепление материала.
Примеры построений сечений методом следов.
- Подведение итогов урока.
Тест.
Ход урока.
- Актуализация опорных знаний.
- Постановка задачи.
- Изучение нового материала.
Вспомним:
— пересечение прямой с плоскостью;
— пересечение плоскостей;
— свойства параллельных плоскостей.
Вопросы к классу:
— Что значит построить сечение многогранника
плоскостью?
— Как могут располагаться относительно друг
друга многогранник и плоскость?
— Как задается плоскость?
— Когда задача на построение сечения
многогранника плоскостью считается решенной?
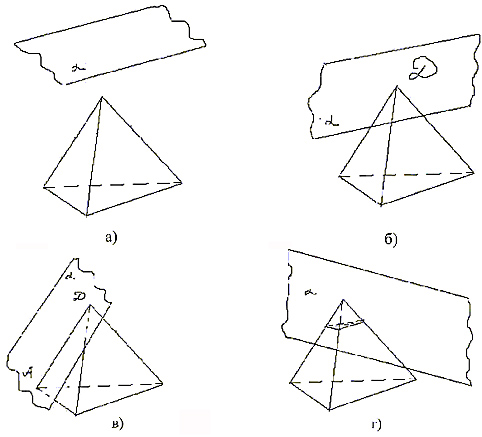
А) Итак, задача состоит в построении
пересечения двух фигур: многогранника и
плоскости ( рис.1). Это могут быть: пустая фигура
(а), точка (б), отрезок (в), многоугольник (г). Если
пересечение многогранника и плоскости есть
многоугольник, то этот многоугольник называется сечением
многогранника плоскостью.
Рис. 1
Будем рассматривать только случай, когда
плоскость пересекает многогранник по его
внутренности. При этом пересечением данной
плоскости с каждой гранью многогранника будет
некоторый отрезок. Таким образом, задача
считается решенной, если найдены все отрезки, по
которым плоскость пересекает грани
многогранника.
Исследуйте сечения куба (рис.2) и ответьте на
следующие вопросы:
Рис. 2
— какие многоугольники получаются в сечении
куба плоскостью? (Важно число сторон
многоугольника);
[ Предполагаемые ответы: треугольник,
четырехугольник, пятиугольник, шестиугольник.]
— может ли в сечении куба плоскостью получиться
семиугольник? А восьмиугольник и т.д.? Почему?
Давайте рассмотрим призму и ее возможные
сечения плоскостью ( на модели). Какие
многоугольники получаются?
Какой можно сделать вывод? Чему равно
наибольшее число сторон многоугольника,
полученного сечением многогранника с
плоскостью?
[ Наибольшее число сторон многоугольника,
полученного в сечении многогранника плоскостью,
равно числу граней многогранника.]
Б) а) Метод следов заключается в построении
следов секущей плоскости на плоскость каждой
грани многогранника. Построение сечения
многогранника методом следов обычно начинают с
построения так называемого основного следа
секущей плоскости, т.е. следа секущей плоскости
на плоскости основания многогранника.
б) Метод вспомогательных сечений
построения сечений многогранников является в
достаточной мере универсальным. В тех случаях,
когда нужный след (или следы) секущей плоскости
оказывается за пределами чертежа, этот метод
имеет даже определенные преимущества. Вместе с
тем следует иметь ввиду, что построения,
выполняемые при использовании этого метода,
зачастую получаются “скученными”. Тем не менее
в некоторых случаях метод вспомогательных
сечений оказывается наиболее рациональным.
Метод следов и метод вспомогательных сечений
являются разновидностями аксиоматического
метода построения сечений многогранников
плоскостью.
в) Суть комбинированного метода построения
сечений многогранников состоит в применении
теорем о параллельности прямых и плоскостей в
пространстве в сочетании с аксиоматическим
методом.
А теперь на примере решения задач рассмотрим метод
следов.
4. Закрепление материала.
Задача 1.
Построить сечение призмы ABCDA1B1C1D1
плоскостью, проходящей через точки P, Q, R (точки
указаны на чертеже (рис.3)).
Решение.
Рис. 3
- Построим след секущей плоскости на плоскость
нижнего основания призмы. Рассмотрим грань АА1В1В.
В этой грани лежат точки сечения P и Q. Проведем
прямую PQ. - Продолжим прямую PQ, которая принадлежит
сечению, до пересечения с прямой АВ. Получим
точку S1, принадлежащую следу. - Аналогично получаем точку S2 пересечением
прямых QR и BC. - Прямая S1S2 — след секущей плоскости
на плоскость нижнего основания призмы. - Прямая S1S2 пересекает сторону AD в
точке U, сторону CD в точке Т. Соединим точки P и U,
так как они лежат в одной плоскости грани АА1D1D.
Аналогично получаем TU и RT. - PQRTU – искомое сечение.
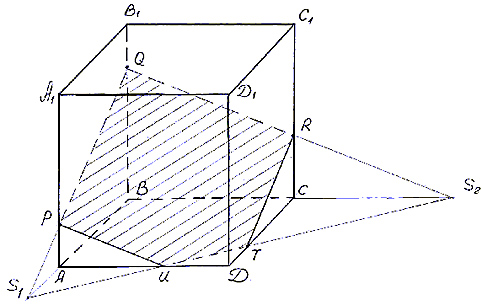
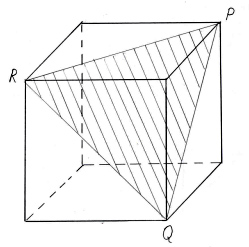
Задача 2.
Построить сечение параллелепипеда ABCDA1B1C1D1
плоскостью, проходящей через точки M, N, P (точки
указаны на чертеже (рис.4)).
Решение.
Рис. 4
- Точки N и P лежат в плоскости сечения и в
плоскости нижнего основания параллелепипеда.
Построим прямую, проодящую через эти точки. Эта
прямая является следом секущей плоскости на
плоскость основания параллелепипеда. - Продолжим прямую, на которой лежит сторона AB
параллелепипеда. Прямые AB и NP пересекутся в
некоторой точке S. Эта точка принадлежит
плоскости сечения. - Так как точка M также принадлежит плоскости
сечения и пересекает прямую АА1 в некоторой
точке Х. - Точки X и N лежат в одной плоскости грани АА1D1D,
соединим их и получим прямую XN. - Так как плоскости граней параллелепипеда
параллельны, то через точку M можно провести
прямую в грани A1B1C1D1,
параллельную прямой NP. Эта прямая пересечет
сторону В1С1 в точке Y. - Аналогично проводим прямую YZ, параллельно
прямой XN. Соединяем Z с P и получаем искомое
сечение – MYZPNX.
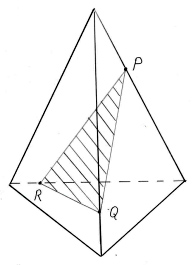
Задача 3 ( для самостоятельного
решения).
Построить сечение тетраэдра DACB плоскостью,
проходящей через точки M, N, P (точки указаны на
чертеже (рис.5)).
Рис. 5
5. Подведение итогов урока.
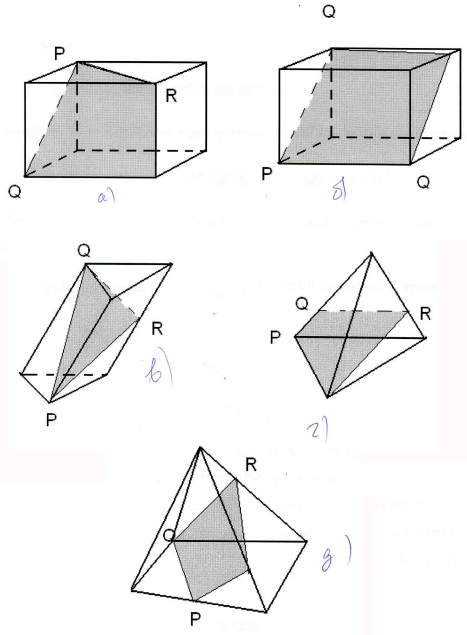
Ответьте на вопрос: являются ли закрашенные
фигуры сечениями изображенных многогранников
плоскостью PQR? И выполните правильное построение
(рис. 6).
Вариант 1.
а)
б)
в)
г)
д)
Вариант 2.
УРОК 2.
Тема урока: НАХОЖДЕНИЕ ПЛОЩАДИ СЕЧЕНИЯ.
Цель урока: познакомить со способами
нахождения площади сечения многогранника.
Этапы урока:
- Актуализация опорных знаний.
- Решение задач на нахождение площади сечения:
Вспомнить теорему о площади ортогональной
проекции многоугольника.
— без использования теоремы о площади
ортогональной проекции многоугольника;
— с использованием теоремы о площади
ортогональной проекции многоугольника.
3. Подведение итогов урока.
Ход урока.
- Актуализация опорных знаний.
- Решение задач.
Вспомним теорему о площади ортогональной
проекции многоугольника: площадь
ортогональной проекции многоугольника на
плоскость равна произведению его площади на
косинус угла между плоскостью многоугольника и
плоскостью проекции.
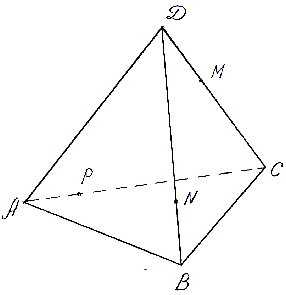
Задача 1.
ABCD – правильная треугольная пирамида со
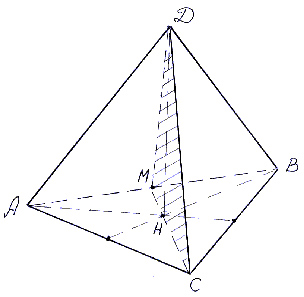
стороной основания AB равной а и высотой DH
равной h. Постройте сечение пирамиды
плоскостью, проходящей через точки D, C и М, где М –
середина стороны АВ, и найдите его площадь (рис.7).
Решение.
Сечением пирамиды является треугольник MCD.
Найдем его площадь.
- Так как основание пирамиды – равносторонний
треугольник и точка М – середина стороны, то СМ
является высотой и тогда, СМ =.
- Площадь треугольника можно найти:
S = 1/2 · DH · CM = 1/2 ·
=
Рис.7
Задача 2.
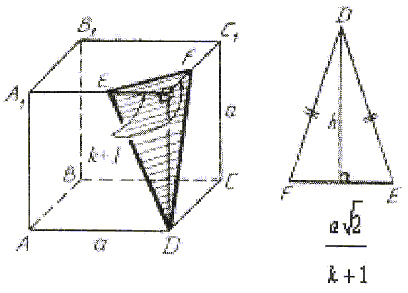
Найти площадь сечения куба ABCDA1B1C1D1
с ребром а плоскостью, проходящей через
вершину D и точки Е и F на ребрах А1D1 и C1D1
соответственно, если A1E = k · D1E и C1F
= k · D1F.
Решение.
Построение сечения:
- Поскольку точки Е и F принадлежат плоскости
сечения и плоскости грани A1B1C1D1,
а две плоскости пересекаются по прямой, то прямая
EF будет являться следом секущей плоскости на
плоскость грани A1B1C1D1
(рис.8). - Аналогично получаются прямые ED и FD.
- EDF – искомое сечение.
Рис.8.
Задача 3 (для самостоятельного решения).
Построить сечение куба ABCDA1B1C1D1
со стороной а плоскостью, проходящей через
точки B, M и N, где Ь – середина ребра АА1, а N –
середина ребра СС1.
Решение.
Сечение строим методом следов.
Площадь сечения находим с помощью теоремы о
площади ортогональной проекции многоугольника.
Ответ: S = 1/2 · a2.
Задание.
Дан куб ABCDA1B1C1D1.
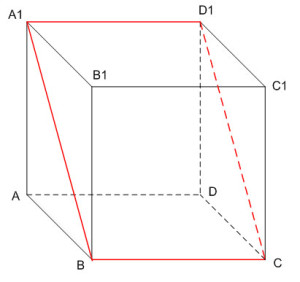
а) Постройте сечение куба плоскостью, проходящей через точки B, A1 и D1.
б) Найдите угол между плоскостями BA1C1 и BA1D1.
Решение:
а) Постройте сечение куба плоскостью, проходящей через точки B, A1 и D1.
Построим плоскость, проходящую через точки B, A1 и D1, т. е. плоскость BA1D1. Точки B и A1 лежат в одной плоскости, поэтому можно провести прямую BA1. Так как ВС параллельна A1D1, то точка С лежит в плоскости BA1D1. Точки С и D1 лежат в одной плоскости, поэтому можно провести прямую СD1. Прямоугольник BA1D1С – искомое сечение.
б) Найдите угол между плоскостями BA1C1 и BA1D1.
Построим плоскость BA1C1. Точки B и A1 лежат в одной плоскости, проведем прямую BA1. Точки A1 и C1 лежат в одной плоскости, проведем прямую A1C1. Точки B и C1 лежат в одной плоскости, проведем прямую BC1. Треугольник BA1C1 – искомое сечение. Так как сторонами этого треугольника являются диагонали граней куба, то треугольник BA1C1 – равносторонний треугольник.
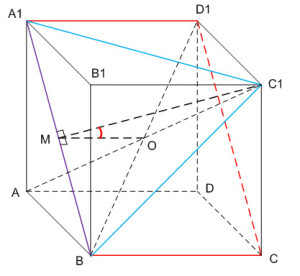
Найдем угол между плоскостями BA1C1 и BA1D1. Плоскости BA1C1 и BA1D1 пересекаются по прямой BA1. Отрезок C1М – высота и медиана треугольника BA1C1, т.е. отрезок C1М перпендикулярен BA1, а также точка М – середина BA1. Найдем точку пересечения диагоналей куба, получим точку О – центр куба. Отрезок МО – средняя линия треугольника BA1D1. Так как A1D1 перпендикулярен BA1, а A1D1 II MO, то МО перпендикулярен BA1.
Следовательно, угол ∠ОМC1 является линейным углом двугранного угла, образованного плоскостями BA1C1 и BA1D1. Угол ∠ОМC1 – искомый угол между плоскостями BA1C1 и BA1D1. Найдем величину этого угла. Углом между двумя плоскостями называется величина острого двугранного угла.
Рассмотрим треугольник ОМC1, найдем стороны этого треугольника. Пусть ребро куба равно 1. МО – средняя линия треугольника BA1D1, тогда МО = 1/2.
Треугольник ВСС1 – прямоугольный (∠С = 90°), по тереме Пифагора
ВС12 = ВС2 + СС12
ВС12 = 2
ВС1 = √2
Треугольник ВМС1 – прямоугольный (∠М = 90°):
По теореме Пифагора:
MC12 = BC12 — BM2
Найдем ОС1, диагональ куба AC1 = √3, тогда ОС1 = √3/2.
По теореме косинусов найдем cos∠ОМC1:
OC12 = MO2 + MC12 – 2·MO·MC1·cos∠ОМC1
Так как за величину угла между двумя плоскостями берется величина острого двугранного угла (взят модуль), получим
Ответ:
Оставить комментарий
Рубрики
- Демоверсия ЕГЭ по информатике
- Демоверсия ЕГЭ по математике
- Демоверсия ОГЭ по информатике
- Демоверсия ОГЭ по математике
- Материалы по аттестации
- Решаем ЕГЭ по математике
- Задание 1
- Задание 10
- Задание 11
- Задание 12
- Задание 13
- Задание 14
- Задание 15
- Задание 16
- Задание 2
- Задание 3
- Задание 4
- Задание 5
- Задание 6
- Задание 7
- Задание 8
- Задание 9
- Решаем ОГЭ по математике
- Задание 21
- Задание 22
- Задание 24
- Скачать экзаменационные варианты по информатике
- ЕГЭ по информатике
- ОГЭ по информатике
- Скачать экзаменационные варианты по математике
- ЕГЭ по математике
- ОГЭ по математике
- Тематическое планирование
План урока:
Понятие двугранного угла и угла между плоскостями
Перпендикулярность плоскостей
Прямоугольный параллелепипед
Трехгранный угол
Многогранный угол
Типичные задачи на углы между плоскостями
Понятие двугранного угла и угла между плоскостями
Напомним, что в планиметрии углом называют фигуру, состоящую из точки и двух лучей, выходящих из нее. Сама точка именуется вершиной угла, а лучи – сторонами угла.
По аналогии в стереометрии рассматривается схожая фигура – двугранный угол. Он состоит из двух полуплоскостей, которые исходят из одной прямой. Каждая из этих полуплоскостей именуется гранью двугранного угла, а их общая прямая – это ребро двугранного угла.
Для обозначения двугранного угла достаточно указать две точки на его ребре, а также ещё по одной точке на каждой грани. Например, на следующем рисунке показан угол САВD:
Двугранные углы часто встречаются в обычной жизни. Например, его образуют двухскатные крыши домов. В стереометрии двугранные угла можно найти в любом многограннике.
Двугранные углы можно измерять. Для этого надо выбрать произвольную точку на ребре угла и на каждой грани построить перпендикуляр, проходящий через эту точку. Через эти два перпендикуляра можно построить единственную плоскость. Угол между двумя перпендикулярами и принимается за величину двугранного угла.
Отдельно отметим, что плоскость, проходящая через перпендикуляры (на рисунке выше это γ) перпендикулярна ребру угла АВ. Это вытекает из признака перпендикулярности прямой и плоскости. Действительно, АВ⊥ВС и АВ⊥BD, поэтому и АВ⊥γ. Построенный угол ∠СBD называют линейным углом двугранного угла.
Понятно, что в каждом двугранном угле можно построить сколько угодно линейных углов:
Здесь помимо ∠ВСD построены линейные углы ∠В’С’D’ и ∠В’’С’’D’’. Однако все эти углы имеют одинаковую градусную меру. Сравним, например, ∠ВСD и ∠В’С’D’. Так как BD⊥AB и B’D’⊥АВ, то BD||B’D’. Аналогично можно прийти к выводу, что ВС||B’C’. Получаем, что стороны углов ∠ВСD и ∠В’С’D’ – это сонаправленные лучи, а потому ∠ВСD и ∠В’С’D’ одинаковы.
Двугранные углы, как и обычные углы, можно разделить на острые (их градусная мера меньше 90°), прямые (они в точности равны 90°) и тупые (которые больше 90°).
Если две плоскости пересекаются, то они образуют сразу 4 двугранных угла. Если среди них есть острый угол, то его величина считается углом между плоскостями. Если же все образуется 4 прямых двугранных угла, то угол между плоскостями принимается равным 90°.
Перпендикулярность плоскостей
В частном случае, когда угол составляет 90°, говорят, что пересекающиеся плоскости перпендикулярны.
Перпендикулярны друг другу пол и стены в доме, смежные грани кубика, стенки коробки. Существует особый признак перпендикулярности плоскостей.
Действительно, пусть плоскости α и β пересекаются по линии n, и в β есть такая прямая m, что m⊥α. Тогда m и n должны пересекаться в какой-нибудь точке К. Проведем в плоскости α через К прямую р, перпендикулярную n. Ясно, что m⊥р, ведь m⊥α. Получается, угол между m и р как раз и является углом между плоскостями α и β, ведь m⊥n и р⊥n. И этот угол равен 90°, ведь m⊥p, ч т. д.
Из доказанного признака вытекает следующее утверждение:
Прямоугольный параллелепипед
Ранее мы уже узнали про параллелепипед. Это фигура с 6 гранями, каждая из которых представляет собой параллелограмм. Особый интерес представляет его частный случай – прямоугольный параллелепипед.
Такую форму имеют многие шкафы, другие предметы мебели, коробки для обуви, небоскребы. Изображают прямоугольный параллелепипед так:
Для обозначения вершин параллелепипеда применяют латинские буквы. Очень часто для вершин одной грани используют 4 буквы без индекса (на рисунке выше это А, В, С, D), а другие 4 вершины обозначают такими же буквами, но с нижним индексом 1: А1, B1, C1 и D1. При этом одноименные вершины (например, А и А1) находятся на одном ребре, которое располагается на рисунке вертикально.
Докажем некоторые свойства прямоугольного параллелепипеда.
Например, ребро АD пересекается с гранями АВВ1А1 и CDD1C1. Значит, оно перпендикулярно этим граням (точнее говоря, оно перпендикулярно плоскостям, проходящим через эти грани). Действительно, AD⊥DC, ведь ∠ADC является углом в прямоугольнике АВСD и потому он прямой. Аналогично и AD⊥DD1, ведь и ADD1A1 – прямоугольник. Получается, что ребро AD перпендикулярно 2 прямым в грани CDD1C1 (которые при этом пересекаются), и потому оно перпендикулярно и всей грани. То же самое можно продемонстрировать для любого ребра прямоугольного параллелепипеда и любой грани, которую она пересекает.
Эти грани пересекаются по ребру А1D1. Этому ребру в свою очередь перпендикулярны ребра АА1 и А1В1, лежащие в гранях ADD1A1 и A1D1C1B1. Значит, ∠АА1В1 и будет углом между этими гранями. Но он составляет 90°, то есть грани перпендикулярны, ч. т. д.
Хотя у прямоугольного параллелепипеда есть 12 граней, многие из них имеют одинаковую длину. Поэтому для описания размеров этой фигуры достаточно указать только три параметра. Обычно их называют длиной, шириной и высотой:
Эти параметры также называют измерениями прямоугольного параллелепипеда. Зная их, можно вычислить длину диагонали прямоугольного параллелепипеда. Для этого используется следующая теорема:
Действительно, пусть есть прямоугольный параллелепипед АВСDA1B1C1D1. Назовем ребро AD его длиной, АВ – шириной, а ВВ1 – высотой. Пусть необходимо найти длину диагонали В1D:
Сначала построим отрезок BD и рассмотрим ∆ABD. Он прямоугольный, и потому для него верна теорема Пифагора:
Теперь перейдем к ∆В1ВD. Так как ребро BB1 перпендикулярно грани ABCD, то ∠В1ВD – прямой. Тогда и ∆В1ВD – прямоугольный, а потому и для него можно записать теорему Пифагора:
Дополнительно отметим уже известный нам факт, что тот прямоугольный параллелепипед, у которого все стороны одинаковы, именуется кубом. Можно дать и такое определение куба:
Трехгранный угол
Выберем в пространстве произвольную точку K. Далее из нее проведем три луча КА, КВ и КС так, чтобы они не находились в одной плоскости:
В результате мы получили фигуру, которую именуют трехгранным углом. Она состоит их трех плоских углов: ∠АКС, ∠АКВ и ∠ВКС. Эти углы так и называются – плоские углы трехгранного угла. Сам же трехгранный угол обозначают четырьмя буквами: КАВС. Обратите внимание, что через каждую пару лучей КА, КВ и КС можно провести плоскость. Таким образом, название «трехгранный» угол показывает, что в точке К сходятся три грани. Чаще всего в стереометрии такой угол возникает при рассмотрении вершин тетраэдра, в котором есть сразу четыре трехгранных угла:
Доказательство. Пусть в пространстве из точки D выходят лучи AD, BD и CD. Важно понимать, что мы можем свободно «передвигать» точки А, В и С по лучам, и величина плоских углов при этом меняться не будет. Если среди плоских углов нет наибольшего, то теорема очевидно выполняется. Поэтому надо рассмотреть лишь случай, когда один из углов – наибольший. Пусть им будет ∠BDC:
Это возможно сделать, ведь ∠BDC > AD, поэтому внутри ∠BDC можно провести луч DK. Далее «сместим» точку А на луче АD так, чтобы DK = AD. Естественно, что при этом плоские углы трехгранного угла никак не изменятся, также как останется верным равенство
Сравним ∆ADC и ∆DKC. У них есть общая сторона DC, одинаковы стороны DK и AD, а также совпадают углы между ними. Значит, эти треугольники равны, и тогда можно записать, что:
Теперь сравним ∆ABD и ∆DBK. У них BD – общая сторона, а DK = AD. При этом BK < AB. В таком случае против меньшей стороны будет лежать меньший угол (смотри примечание после доказательства), то есть
Именно это неравенство и необходимо было доказать.
Примечание. В ходе доказательства было использовано утверждение, что если у двух треугольников две стороны одинаковы, в третьи стороны отличаются, то против меньшей третьей стороны будет располагаться меньший угол:
Это утверждение часто не рассматривается в курсе планиметрии, поэтому есть смысл доказать его отдельно. Действительно, пусть есть ∆АВС и ∆А’B’C’, АС = А’C’ и АВ = A’B’, а СВ < C’B’. Надо показать, что ∠А <∠A’. Для этого выразим стороны СВ и C’B’ (а точнее говоря, их квадраты) с помощью теоремы косинусов:
Из последнего неравенства на основе определения косинуса для углов из интервала от 0° до 180° вытекает, что и
Многогранный угол
Возможен случай, когда из одной точки в пространстве выходят не три, а большее количество лучей, причем образуемые ими углы не располагаются в единой плоскости. Такая фигура именуется многогранным углом. Трехгранный угол можно считать его частным случаем. Также его частными случаями будут четырехгранный угол, пятигранный угол, шестигранный угол и т. д.
Более наглядна следующая демонстрация многогранного угла. Построим на плоскости α произвольный многоугольник. Далее выберем какую-нибудь точку вне плоскости α и соединим ее с вершинами многоугольника с помощью лучей. При этом у нас как раз получится многогранный угол. Если, например, в качестве многоугольника мы использовали пятиугольник, то и получим мы пятигранный угол:
Важно отметить, что в данном случае состоит многогранный угол именно из лучей КА1, КА2, КА3…, а не из одноименных отрезков. То есть многогранный угол – это ни в коем случае не многогранник КА1А2А3А4А5, у него есть только одна вершина – точка К. Многогранник КА1А2А3А4А5 – это пирамида, такая фигура изучается в курсе стереометрии чуть позже. Многоугольник А1А2А3А4А5 – это сечение многогранного угла. Углы ∠А1КА2, ∠А2КА3, ∠А3КА4… – это плоские углы многогранного угла.
Заметим, что на исходный многоугольник на плоскости может быть как выпуклым, так и невыпуклым. Соответственно и многогранный угол может быть как выпуклым, так и невыпуклым:
Так как любой треугольник – это выпуклый многоугольник, то и любой трехгранный угол является выпуклым. В выпуклом угле все его точки лежат по одну сторону от любой плоскости, проходящей, через какие-нибудь два смежных луча угла. Вообще любое сечение многогранного угла представляет собой выпуклый многоугольник.
Докажем важное утверждение:
Для доказательства возьмем произвольный многогранный угол и проведем в нем сечение А1А2А3…Аn, которое будет являться выпуклым многоугольником:
В последнем равенстве в каждой скобке стоят по два плоских угла в тех трехгранных углах, вершины которых совпадают с вершинами многоугольника А1А2А3…Аn. В предыдущей теореме мы выяснили, что эта сумма меньше третьего плоского угла, то есть
В правой части в скобках стоит сумма углов выпуклого n-угольника А1А2А3…Аn. Она, как мы знаем, составляет 180°•(n – 2), то есть
Последнее неравенство и необходимо было доказать.
Типичные задачи на углы между плоскостями
В школьной практике почти не встречаются задачи с многогранными углами, поэтому достаточно понимания и двугранного угла.
Задание. У тетраэдра ABCD все ребра одинаковы. Найдите величину двугранного угла между плоскостями АВС и АСD.
Решение. Отметим на ребре АС точку М, которая является его серединой:
Заметим, что плоскости АВС и АСD пересекаются по прямой АС. Раз все ребра тетраэдра одинаковы, то ∆АВС и ∆АСD – равносторонние. DM и BM – это медианы в ∆АВС и ∆АСD соответственно, ведь M – середина АС. Но раз треугольники равносторонние, то они одновременно являются и высотами, то есть BM⊥AC и DM⊥АС. Тогда ∠DMB как раз и представляет собой линейный угол двугранного угла BАСD. То есть именно его значение нам и надо вычислить (если, конечно, он окажется не больше 90°).
Пусть ребра тетраэдра имеют длину а. Тогда АМ вдвое короче. Найдем из прямоугольного ∆АМD длину MD:
Задание. Двугранный угол равен φ, меньший 90°. На одной из его граней отмечена точка К, которая находится на расстоянии d от другой грани. Каково расстояние между точкой К и ребром двугранного угла?
Решение. Пусть угол образован плоскостями α и β. Опустим из K два перпендикуляра – один на плоскость β в точку Н, а другой на линию пересечения плоскостей в точку Р:
По условию задачи ∠НРК = φ, а HK = d. Нам же надо найти РК. Это можно сделать, применив определение синуса к ∆РНК:
Задание. Верно ли, что плоскость, пересекающая две параллельные плоскости, образует с ними одинаковые углы?
Решение. Пусть есть параллельные друг другу плоскости α и β, а пересекает их плоскость γ. Линию пересечения α и γ обозначим как n, и такую же линию для β и γ обозначим как m:
Заметим, что m и n располагаются в одной плоскости γ и при этом не пересекаются, в противном случае у α и β нашлась бы общая точка, которой быть не должно. Значит, m||n.
Далее проведем в γ прямую р, перпендикулярную n. Раз m||n и р⊥n, то и р⊥m. То есть р – общий перпендикуляр для m и n.
Далее в α через точку пересечения n и p проведем прямую k, перпендикулярную n. Ясно, что k||β. После уже через точку пересечения m и p построим такую прямую k’, что k||k’:
Так как k||β и k||k’, то прямая k’ будет принадлежать плоскости β (по теореме 6 из этого урока). Так как k||k’, m||n и n⊥k, то по теореме о сонаправленных лучах можно утверждать, что и m⊥k’. Тогда углы, отмеченные на рисунке синим цветом – это и есть линейные углы двугранных углов. Они одинаковы, так как являются соответственными при секущей р и параллельных прямых k и k’. Если же двугранные углы равны, то одинаковы и углы между плоскостями, ч. т. д.
Примечание. Доказанный факт можно сформулировать в виде теоремы:
Она может быть использована при решении некоторых сложных задач.
Задание. В прямоугольном ∆АВС АВ и АС – катеты с длиной 7 и 24 соответственно. Через гипотенузу проведена плоскость β, образующая с плоскостью АВС угол 30°. Каково расстояние между точкой А и плоскостью β?
Решение.
Опустим из А перпендикуляр АН на β. Это и будет искомое нами расстояние. Также в ∆АВС построим высоту AD. Заметим, что раз АН⊥β, то по определению и АН⊥HD. Можно сказать, что HD – это проекция AD на β. Раз прямая ВС перпендикулярна наклонной AD, то она одновременно будет перпендикулярна и наклонной HD по обратной теореме о трех перпендикулярах.
Плоскости АВС и β пересекаются по прямой ВС, АD⊥ВС и HD⊥BC. Получается, что ADH – это как раз угол между АВС и β, и по условию он составляет 30°.
По теореме Пифагора вычислим гипотенузу ВС:
Теперь перейдем к ∆AHD. Он также прямоугольный (∠Н = 90°). Используем для него тригонометрию:
Задание. Известны измерения прямоугольного параллелепипеда. Его длина составляет 90 см, ширина – 20 см, а высота – 60 см. Какова длина диагонали такого параллелепипеда?
Решение. Обозначим измерения буквами а, b, с, а диагональ буквой d. Достаточно просто воспользоваться формулой:
Далее рассмотрим несколько задач, в которых надо найти угол между плоскостями, находящимися в кубе с ребром, чья длина составляет единицу.
Задание. Вычислите угол между гранью ADHЕ и сечением АBGН:
Решение. Заметим, что сечение АВGH содержит прямую АВ. Но АВ – это перпендикуляр к АЕНD. Если АВGH содержит перпендикуляр к ADH, то эти две плоскости перпендикулярны, и угол между ними составляет 90°.
Ответ: 90°.
Задание. Определите угол между гранью ADHE и сечением ADGF:
Решение. Две рассматриваемые плоскости пересекаются по ребру AD. Ребра DH и AD перпендикулярны как стороны квадрата. Так как AD – это перпендикуляр к грани СDHG, то AD⊥DG. Получается, что ∠HDG – это и есть искомый угол. Его величина равна 45°, ведь это угол между диагональю квадрата и его стороной.
Ответ: 45°.
Задание. Вычислите угол между сечениями АВGH и EFCD:
Решение. Пересекаются эти две плоскости по прямой KP, где K и P – точки пересечения диагоналей квадратов BFGH и AEHD. Докажем, что отрезки KG и KC перпендикулярны KP.
Действительно, рассмотрим четырехугольник АВGH. Ребра АВ и GH перпендикулярны граням AEHD и BFGH, поэтому все углы в АВGH – прямые, то есть это прямоугольник и BG||AH. Теперь рассмотрим четырехугольник АВKP. Стороны BK и AP параллельны и равны как половины равных отрезков BG и AH. Значит, BKAP – параллелограмм. Но в нем есть прямые углы ∠В и ∠А, поэтому BKAP – прямоугольник. Аналогично можно показать, что и KGHP – прямоугольник. Это и приводит к выводу о том, что KG⊥KP и PH⊥KP. Поэтому ∠СKG и является искомым углом между сечениями. Он является углом между диагоналями квадрата, то есть равен 90°.
Ответ: 90°.
Задание. Найдите угол между сечением AFH и гранью AEHD:
Решение. Обозначим середину диагонали AH буквой K. Докажем ∠EKF – искомый нами угол:
Действительно, плоскости AHD и AFH пересекаются по прямой AH. EK – медиана в равнобедренном ∆AEH с основанием AH, поэтому она также является и высотой, то есть EK⊥AH. AF и FH – диагонали в равных квадратах ABFE и EFGH, поэтому эти диагонали одинаковы. Значит, ∆AFH – равнобедренный, и поэтому его медиана FK также перпендикулярна основанию AH. Получается, что ∠EKF и является искомым. Вычислить его можно из ∆EKF.
Сначала найдем длину EK. В прямоугольном ∆AEK ∠KAE составляет 45° (угол между диагональю и стороной квадрата), поэтому
Задание. Вычислите угол между гранью BCGF и сечением AFH:
Решение. Вспомним, что в предыдущей задаче мы уже вычислили угол между гранью АЕHD и тем же сечением АFH. Но грани AEHD и BCFG параллельны, поэтому АFH должна пересекаться их под одним и тем же углом. Поэтому ответ этой задачи совпадает с ответом к предыдущей задаче.
Ответ: ≈ 54,74°.
Задание. Чему равен угол между сечениями АСH и AFGH?
Решение. Пусть диагонали СН и DG пересекаются в точке К. Точка K будет принадлежать обоим сечениям, как и точка А. Значит, сечения пересекаются по линии АК. Проведем в сечении AFGH через точку K прямую, перпендикулярны АК и пересекающую FG в какой-то точке Р (позже мы убедимся, что прямая действительно должна пересекать отрезок FG):
Докажем, что ∠CPK и является углом между сечениями. Мы специально провели РК так, что РК⊥АК. Теперь посмотрим на ∆АСН. Он равносторонний, ведь его стороны АС, СН и DH – это диагонали равных квадратов (граней куба). Прямая АК – медиана, ведь K – точка пересечения диагоналей квадрата СDHG, которая делит диагонали пополам. Но раз ∆АСН равносторонний, то его медиана – это ещё и высота, то есть АК⊥РК. Итак, АК⊥СК и АК⊥РК, поэтому ∠CPK – это угол между сечениями. Для его вычисления необходимо найти все стороны в ∆РСК и далее применить теорему косинусов.
Проще всего найти СК. ∆СKD – прямоугольный (∠К = 90°), а ∠СDK составляет 45° (угол между стороной и диагональю в квадрате). Тогда можно записать, что
Отдельно отметим, что отрезки GK и KD имеют такую же длину, ведь диагонали в квадрате (а значит и их половины) одинаковы.
Для нахождения РК покажем отдельно плоскость AFG, то есть красное сечение:
Обозначим ∠KAD как φ. Тогда ∠АКD будет составлять 90 – φ. Углы ∠АКD, ∠АKP и ∠PKG в сумме дают 180°, что позволяет найти ∠PKG:
Получилось, что у ∆АКD и ∆PKG есть по два одинаковых угла (φ и 90°). Значит, они подобны. Составим такую пропорцию:
Теперь можно вернуться ко всему кубу и найти отрезок РС. Здесь снова можно применить теорему Пифагора, но уже к ∆PCG:
Теперь для ∆PCK мы можем записать теорему косинусов
Неожиданно мы доказали, что два построенных сечения перпендикулярны друг другу. Прийти к этому выводу можно было и иначе. Достаточно было бы показать, что прямая CH – это перпендикуляр к сечению AFGD. Попробуйте сделать это самостоятельно.
Ответ: 90°.
Задание. Вычислите угол между сечениями BDHF и ADGF:
Решение. У сечений общими являются точки F и D. Значит, именно по прямой FD они пересекаются.
Опустим в синей сечении BDHF перпендикуляр на FD, который упадет в некоторую точку K:
Докажем, что отрезок GK также перпендикулярен FD. Действительно, BK – это высота в ∆BDF. Но ∆BDF и ∆GDF равны, ведь они одинаковы все три стороны (FD – общая сторона, BF и FG – ребра куба, BD и DG – диагонали на гранях куба). В равных треугольниках высоты должны делить стороны на равные отрезки, поэтому высота, опущенная из G на FD, также разделит FD на отрезки FK и KD. То есть она просто упадет в точку K. Это и значит, что KG – высота. Получается, что нам надо вычислить ∠BKG.
Сначала найдем длину диагоналей BD и BG. Можно применить теорему Пифагора для ∆BFG:
KG имеет ту же длину, ведь KG и BK – одинаковые высоты в равных треугольниках ∆BDF и ∆GDF.
Теперь используем теорему косинусов для ∆BKG:
Мы вычислили двугранный угол, но он оказался больше 90°. Это значит, угол между плоскостями равен не 120°, а 180° – 120°, то есть 60°.
Ответ: 60°.
Сегодня мы познакомились с понятием двугранного угла, научились вычислять углы между плоскостями. В частном случае вместо вычисления угла можно просто доказать перпендикулярность плоскостей.