Как найти угол сферического треугольника

Сферические треугольники решение и формулы (Таблица)

Сферические треугольники.

На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара, и сферической поверхности. Сторонами а, b, с сферического треугольника  называют те углы  между лучами, которые меньше 180°. Каждой стороне треугольникасоответствует дуга большого круга на поверхности шара (рис. 1). Углы A, В, С сферического треугольника, противолежащие сторонам а, b, с соответственно, представляют собой, по определению, меньшие, чем 180°, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лу­чами.

Свойства сферических треу­гольников.

Каждая сторона и угол сфери­ческого треугольника по определению мень­ше 180°. Геометрия на поверхности шара являет­ся неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°, сумма углов заключена между 180° и 540°. В каждом сферическом треуголь­нике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.

Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):

•   тремя сторонами,
•   тремя углами,
•   двумя сторонами и заключенным между ними углом,
•   стороной и двумя прилежащими к ней углами.

Решение сферических треугольников (Таблица)

(смотрите формулы ниже и рис. 1 выше)

Случай	Даны	Формулы для вычисления	Условия существования решения
1	Три стороны а, Ь, с	А, В, С из (8) и циклической перестановки	Сумма двух сторон должна быть больше третьей
2	Три угла А, В, С	а, Ь, с из (8) и циклической перестановки	Сумма двух углов должна быть меньше 180° плюс третий угол
3	Две стороны и заключенный между ними угол b, с, А	из (6), затем В и С; а из (7), (8) или (4)
4	Два угла и заключенная между ними сторона В, С, а	из (6), затем b и с; А из (7), (8) или (5)
5	Две стороны и противолежащий одной из них угол Ь, с, В	С из (3); А и а из (6)	Задача имеет одно или два решения, если sin с sin В ≤ sin b. Сохраняются те из величин с, для которых А — В и а — b имеют одинаковый знак; A + B — 180° и а + b — 180° также должны быть одного знака
6	Два угла и противолежащая одному из них сторона В, С, b	с из (3); А и а из (6)	Задача имеет одно или два решения, если sin b sin С ≤ sin В. Сохраняются те из величин с, для которых A — В и а — b имеют одинаковый знак; A + В — 180° и а + Ь — 180° также должны быть одного знака

Формулы для решения сферических треугольников

В следующих ниже соотношениях А, В, С являются углами, противолежащими соответственно сторонам а, b, с сферического треугольника. «Радиусы» описанного и вписанного конусов обозначены соответственно через г и р. Формулы, не включенные в перечень, могут быть получены одновременной циклической перестановкой А, В, С и а, Ь, с. Таблица выше позволяет вы­числять стороны и углы любого сферического треугольника потрем подходящим образом заданным сторонам и/или углам. Неравенства, отмеченные в начале п. 2, должны быть приняты во внимание, для того чтобы исключить посторонние результаты при решении треугольников.

	теорема синусов	(1)
	теорема косинусов для сторон	(2)
	теорема косинусов для углов	(3)
	аналогии Непера	(4)
	аналогии Деламбра и Гаусса	(5)
	формулы половинных углов	(6)
		(7)
		(8)
	уравнение Люилье	(9)
	Некоторые тригонометрические соотношения становятся особенно удобными для вычислений с помощью логарифмов, если в них использованы новые тригонометрические функции	(10)
	Таким образом, если имеются в наличии таблицы функции hav, то для решения сфе­рических треугольников можно использовать эти формулы:	(11)
Другие аналогичные соотношения можно получить циклической перестановкой

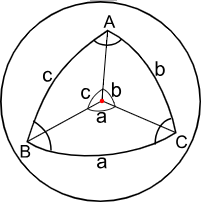
Часть
сферы, заключенная между тремя попарно
пересекающимися дугами больших кругов,
называется сферическим
треугольником.

Вершины
сферического
треугольника
обозначаются
заглавными буквами А,
В, С, а
противолежащие им стороны одноименными
малыми буквами а,
b, с. Стороны
и углы при вершинах называются
элементами
сферического
треугольника.

Будем
рассматривать сферические треугольники,
элементы которых меньше 180°. Такие
треугольники называются треугольниками
Эйлера.

Для
того, чтобы решить сферический треугольник
необходимо знать три из шести его
элементов. При решении сферических
треугольников будем использовать четыре
основные теоремы сферической тригонометрии.

1.
Теорема косинуса
стороны.

В
сферическом треугольнике косинус
стороны равен произведению косинусов
двух других сторон плюс произведение
синусов тех же сторон на косинус угла
между ними:

cos
а=
cos
b
cos
с
+
sin b
sin
с
cos
A

2.
Теорема
косинуса
угла.

В
сферическом треугольнике косинус угла
равен отрицательному произведению
косинусов двух других углов плюс
произведение синусов этих углов на
косинус стороны между ними:

cos
А
= —
cos В
cos
С
+
sin В
sin
С cos a

В
сферическом треугольнике на рис.3.1,
элементы, отмеченные двумя черточками,
лежат рядом. В данном случае сторона
а
и
угол А
называются
крайними элементами, а сторона с
и
угол В
называются
средними элементами.

3.
Теорема котангенсов
или
четырех
рядом лежащих элементов;

В
сферическом треугольнике для четырех
рядом лежащих элементов котангенс
крайнего угла, умноженный на синус
среднего угла равен произведению
котангенса крайней стороны на синус
средней стороны, минус произведение
косинусов средних элементов

ctgA
sin
В
= ctg a sin
с
— cos
В
cos
с

4.
Теорема синусов:

В
сферическом треугольнике отношение
синуса угла к синусу противолежащей
стороны есть величина постоянная:

sinA/sina=sinB/sinb=sinC/sinc
= M,

где
М-
модуль
сферического треугольника.

Будем
использовать независимое
решение,
т.е. определять искомые элементы только
через заданные, применяя для этого
первые три теоремы. Для проверки
правильности решения используется
теорема синусов.

Решение
сферических треугольников выполним в
следующем порядке:

1.
Записываем заданные элементы
треугольника. Если требуется, для
используемого типа калькулятора, данные
записать в градусах и десятичных долях
градуса (не менее трех значащих цифр
после запятой).

2.
Начертить произвольный сферический
треугольник и отметить на нем заданные
элементы.

3.
С помощью основных теорем сферической
тригонометрии установить связь между
заданными и искомыми элементами, помня
о том, что решение должно быть независимым.

4.
Привести формулы к рабочему виду, для
чего неизвестный элемент перенести в
левую часть, а известные в правую.
Преобразовать формулы таким образом,
чтобы в них присутствовали только те
прямые тригонометрические функции,
которые можно вычислить с помощью
данного калькулятора (как правило — sin,
cos, tg).

5.
Найти
значения искомых элементов, стараясь
при этом не делать лишних промежуточных
записей (лучше вообще обходиться без
них). Если калькулятор дает искомые
элементы в градусах и долях градусов,
перевести десятичные доли градусов в
минуты и доли минут. Следует помнить,
что главное значение функции arctg
находится
в интервале от -90° до +90″. Если полученное
значение arctg
отрицательное,
необходимо к результату прибавить 180°.

6.
Произвести контроль по теореме синусов.

7.
Записать ответ.

Пример
3.1.
В
сферическом треугольнике заданы две
стороны и угол между ними: а
=117°14,5′;
B = 60°08,9′; c=77°41,3′. Определить: А,
b, С.

Решение.

Дано:

а=
117°
14,5′ =117,242°;

B=
60°08,9′ = 60,148°;

с=
77°41,3’= 77,688°.

Найти:
А,
b, С.

Основные
формулы:

ctgA
sin
В
=
ctg a
sin
с
— cos В
cos
с;

cos
b
=
cos a cos с
+ sin b sin c cos B;

ctg
С
sin
В
= ctg с
sin a
—
cos a cos B.

Рабочие
формулы:

tgA
=
sin В
/ (sin с/tg
a — cos В
cos c);
A=125°04,9′;

cos
b
=
cos a cos с
+ sin a
sin
с
cos B;
b=
70°26,5′;

tg
С
= sin B / (sin a/
tg
с
— cos a
cos
B);
C=
64°03,6′.

Проверка:

sin
A / sin a = 0,92042; sin В/Sin
b = 0,92042; sin С
/sin
с
= 0,92042,

Ответ:

A=125°04,9′;
b=70°26,5′;
C=64°03,6′.

В
задачах №№ 61-120 заданы две стороны и
угол сферического треугольника: а,
b, С. Определить
два угла и сторону: А,
В, с.

№	а	b	С	№	а	b	С
61	83°54.3′	90°18.1	162°56.6′	66	92°28.8′	92°20.3′	160°54.4′
62	86 56.9	11 53.2	34 46.1	67	88 59.1	7 49.1	28 39.5
63	20 36.9	62 48.4	138 31.9	68	21 59.1	64 50.6	142 36.1
64	59 27.2	66 49.9	115 15.2	69	61 29..4	62 45.7	110 08.6
65	32 02.4	35 18.7	83 35.2	70	27 58.2	37 20.9	87 39.4

№	а	b	С	№	а	b	С
71	22°40.2′	64°51.7′	144°38.2′	96	0°54.1′	16°10.7′	66°45.1′
72	102 03.1	94 22.5	158 22.2	97	1 01.6	2 10.7	40 49.3
73	84 54.9	9 51.2	32 43.7	98	36 12.4	0 54.2	55 46.8
74	23 21.3	66 58.2	145 40.3	99	92 01.3	2 14.3	78 53.8
75	63 31.6	59 41.5	104 30.7	100	38 17.6	1 32.8	2 14.5
76	23 54.1	38 43.5	92 10.6	101	1 50.6	0 43.8	45 10.4
77	112 33.2	97 23.5	155 45.1	102	2 15.4	3 01.9	73 46.9
78	80 50.7	12 45.3	37 46.7	103	0 29.5	3 11.7	86 56.8
79	24 43.5	67 21.3	151 10.4	104	56 23.9	73 12.7	122 57.6
80	65 33.8	54 37.3	99 40.5	105	38 08.7	33 10.4	78 23.7
81	19 49.8	42 45.2	96 13.4	106	77 25.5	88 54.2	162 55.7
82	122 35.4	97 45.2	152 46.8	107	85 55.8	12 42.7	39 40.5
83	76 46.5	12 10.7	41 34.1	108	19 55.8	63 57.1	132 36.3
84	17 47.7	43 56.2	98 10.5	109	58 26.1	69 01.2	120 13.6
85	26 05.7	69 10.8	156 23.7	110	34 04.5	35 55.1	80 54.1
86	67 36.1	52 53.7	93 11.4	111	87 27.7	92 20.4	158 36.2
87	15 45.6	44 10.8	101 54.2	112	87 58.1	10 10.6	29 14.7
88	132 37.6	99 54.8	150 35.7	113	21 18.2	64 39.7	142 54.2
89	72 42.3	16 10.4	46 51.8	114	60 28.3	65 10.4	114 56.7
90	27 27.9	73 14.2	159 42.1	115	30 00.3	37 51.2	87 42.9
91	69 38.2	47 45.2	88 35.9	116	97 29.9	94 13.5	153 26.8
92	1141.4	46 23.8	104 10.2	117	86 57.1	9 15.7	32 18.4
93	142 39.8	101 56.4	148 23.1	118	62 30.5	59 41.7	109 46.2
94	68 38.1	19 14.5	50 00.5	119	25 56.1	39 35.5	90 57.8
95	28 50.1	76 35.2	163 14.5	120	10 32.1	96 47.3	155 14.7

В
задачах №№ 121-150 заданы три
стороны сферического треугольника a,
b ,c. Определить
три угла А,
В, С.

№	a	b	с	№	a	b	с
121	75°09.1′	123°14.2′	57°12.5′	129	32°17.8′	59°13.5′	84°22.1′
122	62 30.3	101 34.7	69 40.4	130	63 01.7	141 10.2	92 47.6
123	98 38.8	73 22.6	51 47.3	131	33 48.6	61 29.4	83 15.7
124	78 40.2	46 23.5	109 01.2	132	88 27.5	50 40.7	122 14.1
125	38 42.6	31 45.7	63 10.2	133	43 16.1	101 52.5	86 10.4
126	92 13.5	73 45.8	138 54.5	134	60 59.3	75 12.2	105 30.6
127	28 51.3	67 40.5	77 12.9	135	73 18.6	87 10.7	99 12.6
128	87 20.4	75 12.3	122 14.5	136	35 43.6	40 15.7	50 22.4

№	а	b	с	№	а	b	с
137	70°19.3′	125°19.4′	88°40.9′	144	76°01.3′	59°12.4′	30°40.7′
138	62 34.5	109 11.7	73 54.8	145	38 34.6	13122.7	97 20.5
139	57 14.5	68 12.7	101 35.6	146	111 12.4	73 10.2	61 45.7
140	24 42.9	15 10.7	33 54.6	147	1133.6	29 12.7	36 40.2
141	37 57.1	64 25.3	77 11.9	148	56 31.5	122 10.4	102 36.6
142	57 13.7	102 04.5	83 45.7	149	78 23.3	53 50.1	85 36.9
143	100 34.5	122 10.4	63 24.8	150	35 17.4	17 45.2	27 10.1

В
задачах №№ 151-180 заданы три
угла сферического треугольника A, В,
С. Определить
три стороны а,
b ,с.

№	А	В	С	№	А	В	С
151	101°25.4′	69°10.7′	55°45.6′	166	58°27.4′	61°45.7′	72°30.5′
152	126 04.9	133 57.1	128 18.4	167	101 28.2	43 55.7	82 14.3
153	113 50.4	13135.6	139 11.7	168	79 09.5	66 30.4	136 55.1
154	87 42.1	81 55.6	55 45.7	169	28 45.2	85 23.4	9751.8
155	111 10.7	56 45.3	87 36.8	170	60 09.2	72 45.1	56 41.8
156	38 40.6	98 12.5	65 14.7	171	128 12.5	137 23.8	145 54.1
157	81 33.5	62 45.1	74 36.7	172	8129.2	96 34.2	116 42.7
158	129 11.1	130 25.7	108 45.8	173	151 29.4	124 30.2	140 22.7
159	64 18.1	104 10.3	82 45.1	174	63 18.6	57 52.4	70 35.9
160	129 02.3	125 23.8	139 54.2	175	93 27.8	110 50.2	81 22.6
161	58 18.8	97 51.2	76 13.4	176	102 50.1	100 17.5	136 44.3
162	83 32.8	55 13.4	70 42.1	177	148 07.3	101 42.8	125 16.7
163	116 30.7	130 25.4	119 54.2	178	133 09.5	80 15.2	109 42.1
164	69 18.7	97 05.5	39 53.1	179	83 11.7	80 25.6	116 45.9
165	120 07.1	150 25.5	140 40.4	180	59 10.2	73 52.1 122 35.2

В
задачах №№ 181-210 заданы сторона и два
угла сферического треугольника а,
В, С. Определить
угол и две стороны А,
b ,с.

№	а	В	С	№	а	В	С
181 182 183 184	130°11.9′ 45 40.6 102 42.2 18 10.9	94°55.1′ 55 14.2 80 15.5 40 12.6	54°33.2′ 137 12.4 77 51.3 161 35.7	185 186 187 188	75°12.5′ 130 56.7 47 42.8 104 44.4	70°14.3′ 96 55.1 55 11.4 82 35.6	104°22.7′ 47 31.4 131 56.9 77 23.9

№	а	В	С	№	а	В	С
189	20°13.1′	42°57.1′	160°23.7′	200	81°19.1′	73°45.1′	98°14.7′
190	77 14.7	71 36.4	105 19.8	201	138 20.7	98 11.4	46 49.1
191	134 16.3	97 33.5	48 25.6	202	53 49.4	60 12.5	126 45.7
192	49 45.1.	56 13.4	132 10.4	203	110 51.1	88 15.7	67 13.5
193	106 46.6	86 11.3	72 55.1	204	26 19.7	44 23.9	161 13.5
194	22 15.3	42 56.4	161 13.5	205	83 21.3	74 55.2	99 10.5
195	79 16.9	72 14.3	105 46.2	206	140 22.9	100 55.1	38 14.6
196	136 18.5	101 50.4	48 13.7	207	55 51.6	55 51.6	130 41.8
197	51 47.2	58 55.1	131 16.2	208	15 07.6	39 34.3	170 32.8
198	108 48.8	87 14.2	75 31.9	209	72 09.2	66 36.6	111 23.4
199	24 17.5	43 12.6	161 55.1	210	129 10.8	98 11.4	50 13.7

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Сферические треугольники решение и формулы (Таблица)

Сферические треугольники.

На поверхности шара кратчайшее расстояние между двумя точками измеряется вдоль окружности большого круга, т. е. окружности, плоскость которой проходит через центр шара. Вершины сферического треугольника являются точками пересечения трех лучей, выходящих из центра шара, и сферической поверхности. Сторонами а, b, с сферического треугольника называют те углы между лучами, которые меньше 180°. Каждой стороне треугольникасоответствует дуга большого круга на поверхности шара (рис. 1). Углы A, В, С сферического треугольника, противолежащие сторонам а, b, с соответственно, представляют собой, по определению, меньшие, чем 180°, углы между дугами больших кругов, соответствующими сторонам треугольника, или углы между плоскостями, определяемыми данными лу­чами.

Свойства сферических треу­гольников.

Каждая сторона и угол сфери­ческого треугольника по определению мень­ше 180°. Геометрия на поверхности шара являет­ся неевклидовой; в каждом сферическом треугольнике сумма сторон заключена между 0 и 360°, сумма углов заключена между 180° и 540°. В каждом сферическом треуголь­нике против большей стороны лежит больший угол. Сумма любых двух сторон больше третьей стороны, сумма любых двух углов меньше, чем 180° плюс третий угол.

Сферический треугольник единственным образом определяется (с точностью до преобразования симметрии):

• тремя сторонами,
• тремя углами,
• двумя сторонами и заключенным между ними углом,
• стороной и двумя прилежащими к ней углами.

Решение прямоугольных и четвертных сферических треугольников

Прямоугольные и четвертные сферические треугольники являются частным случаем косоугольных сферических треугольников.

Прямоугольным сферическим треугольником называется такой сферический треугольник, у которого один из углов равен 90°.

Четвертным сферическим треугольником называется такой сферический треугольник, у которого одна из сторон равна 90°.

К этим треугольникам применимы все правила и алгоритмы решения косоугольных сферических треугольников.

Прямоугольные треугольники можно решать по основным формулам сферической тригонометрии. Так как один из углов равен 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Но более рационально производить решение по правилам Модюи-Непера, почти полностью исключающим промежуточные преобразования, а значит и ускоряющим решение (

Пример 3.2).

Правила Модюи-Непера формулируются следующим образом:

1) В прямоугольном сферическом треугольнике косинус любого среднего элемента равен произведению котангенсов крайних смежных с ним элементов.

2) Косинус отдельно лежащего элемента сферического треугольника равен произведению синусов двух не смежных с ним рядом лежащих элементов.

В обоих правилах принято, что катеты лежат рядом друг с другом и вместо катетов надо брать их дополнения до 90°.

Формул такого вида 10. Все они однотипны, поэтому для примера приведём четыре характерных:

При А=90°

cos a = ctg B ctg C

cos B = ctg a ctg (90° – c)

cos (90° – c) = sin C sin a

cos a = sin (90° – b) sin (90° – c)

Следовательно, в задаче на прямоугольный треугольник, надо задать два элемента и указать, какой угол равен 90°.

Пример 3.2

1) Выполняем схематический чертёж и помечаем данные и искомые элементы.

2) Подбираем необходимые формулы.

(по основным формулам сферической тригонометрии)

A, B – формула котангенсов;

c – формула косинуса стороны;

1. ctg A sin C = ctg a sin b – cos b cos C

2. ctg B sin C = ctg b sin a – cos a cos C

3. cos c = cos a cos b + sin a sin b cos C

3) Преобразовываем формулы и производим анализ на знаки. После преобразований независимо от первоначальных формул результат одинаков.

ctg A = ctg a sin b

ctg B = ctg b sin a

cos c = cos a cos b

(по правилам Модюи-Непера)

cos (90 – a) = ctg B ctg (90 – b)

cos (90 – b) = ctg A ctg (90 – a)

cos c = sin (90 – b) sin (90 – a)

ctg A = ctg a sin b

ctg B = ctg b sin a

cos c = cos a cos b

Не забываем, что отношение, это разность логарифмов

lg sin A = 9.76234 lg sin B = 9.99528 lg sin С =10,00000

lg sin a = 9.75263 lg sin b = 9.98557 lg sin c = 9.99029

0,00971 0.00971 0.00971

Четвертные сферические треугольники, как и прямоугольные можно решать по основным формулам сферической тригонометрии. Т.к. одна из сторон равна 90°, формулы значительным образом упрощаются (sin(90°)=1, cos(90°)=0) и состоят, как правило, из двух множителей. Возможен и другой путь решения: свести четвертной треугольник к полярному прямоугольному и производить решение по правилам Модюи-Непера.

Сферические треугольники ABC и A₁B₁C₁ называются полярными, если их стороны и углы связаны следующими соотношениями:

т.е. сумма угла данного треугольника с противоположной стороной полярного ему треугольника равна 180°.

Пример 3.3

Дано: a =31°15.2′, C = 120°15.4′

1) Выполняем схематический чертёж и помечаем данные и искомые элементы.

2) Подбираем необходимые формулы. (по основным формулам сферической тригонометрии)

A – теорема синусов

B – формула котангенсов;

c – формула косинуса стороны;

1.

2. ctg B sin C = ctg b sin a – cos a cos C

3. cos c = cos a cos b + sin a sin b cos C

3) Преобразовываем формулы, отделяем неизвестные, а так же производим анализ формулы на знаки.

1. sin A = sin a sin C

2. tg B = — cos a tg C

3. tg b = — ctg a sec C

а 90° sin C (+), sec C и tg C ( – )

Так как во всех формулах результат положителен, все искомые величины находятся в первой четверти.

4) Составляем схему вычислений и производим вычисления с использованием таблиц 5-а МТ-75(63) Таблица 3.6. Подробности использования таблиц приведены в пояснениях к таблицам. Что бы не менять наименования функций для аргументов больших 90° при входе в таблицу берём их дополнения до 180°.

lg	lg	lg
a=31°15.2′ C=120°15.4′	sin sin	9.71502 9.93640	cos tg	9.93191 0.23408	ctg sec	0.21687 0.29768
sin A	9.65142	tg B	0.16599	tg b	0.51455
A	26°37.5′	B	55°41.5′	b	72°59,8′
A=26°37.5′	B=55°41.5′	b=72°59,8′

5) Производим контроль вычислений по теореме синусов. Проверку можно производить как на калькуляторе, так и при помощи таблиц логарифмов[1].

lg sin a = 9.71502 lg sin b = 9.98059 lg sin с =10.00000

lg sin A = 9.65142 lg sin B = 9.91699 lg sin C = 9.93640

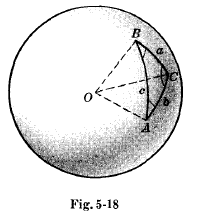
Сферический треугольник

Сферический треугольник ABC расположен на поверхности сферы как показано на рисунках.

Стороны a, b, c (являющиеся дугами больших кругов) измеряются величинами опирающихся на них центральных углов.
A, B, C есть углами, противоположными сторонам a, b, c соответственно.

Площадь сферического треугольника $ABC = (A + B + C — pi)R^2$
где R — радиус сферы.

Отношение между сторонами и углами сферического треугольника

Правило косинусов
cos a = cos b ⋅ cos c + sin b ⋅ sin c ⋅ cos A
cos A = — cos B ⋅ cos C + sin B ⋅ sin C ⋅ cos a
с подобными результатами при использовании других сторон и углов.

с подобными результатами при использовании других сторон и углов.

Подобные утверждения справедливы и для других углов и сторон.

где $S = frac<2>$.
Подобные утверждения справедливы и для других углов и сторон.

Правила Непера для прямоугольного сферического треугольника

За исключением прямоугольного угла C, есть пять частей сферического треугольника ABC, которые приведены на рис. 5-19 и обозначены как a, b, A, c, B.

Предположим, что эти части расположены по кругу, как на рис. 5-20, где мы допишем префикс co (означающий дополнение) к гипотенузе c и углам A и B.

Любая из этих частей круга называется средняя часть, две другие соседние части называются смежные части и две другие оставшиеся части называются противоположные части.

Синус любой средней части равен произведению тангенсов смежных частей.

Синус любой средней части равен произведению косинусов противоположных частей.

Пример:
Так как co-A = 90° — A, co-B = 90° — B, мы имеем
sin a = tg b ⋅ tg(co-B) или sin a = tg b ⋅ ctg B
sin(co-A) = cos a ⋅ cos(co-B) или cos A = cos a ⋅ sin B.