Определение
Выпуклый многоугольник называется правильным, если все его стороны равны и все его углы равны.
Замечание
Т.к. сумма всех углов (n)–угольника равна (180^circ(n-2)), то каждый угол правильного (n)–угольника равен [alpha_n=dfrac{n-2}n cdot 180^circ]
Пример
Каждый угол правильного четырехугольника (т.е. квадрата) равен (dfrac {4-2}4cdot 180^circ=90^circ);
каждый угол правильного шестиугольника равен (dfrac{6-2}6cdot
180^circ=120^circ).
Теоремы
1. Около любого правильного многоугольника можно описать окружность, и притом только одну.
2. В любой правильный многоугольник можно вписать окружность, и притом только одну.
Следствия
1. Окружность, вписанная в правильный многоугольник, касается всех его сторон в серединах.
2. Центры вписанной и описанной окружности у правильного многоугольника совпадают.
Теорема
Если (a) – сторона правильного (n)–угольника, (R) и (r) – радиусы описанной и вписанной окружностей соответственно, то верны следующие формулы: [begin{aligned}
S&=dfrac n2ar\
a&=2Rcdot sindfrac{180^circ}n\
r&=Rcdot cosdfrac{180^circ}n end{aligned}]
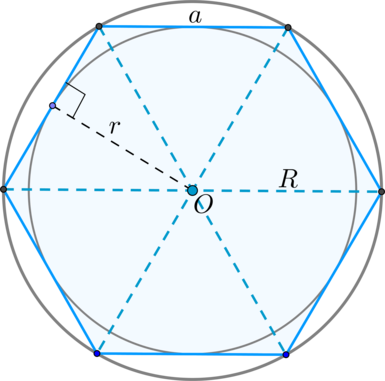
Свойства правильного шестиугольника
1. Сторона равна радиусу описанной окружности: (a=R).
2. Радиус описанной окружности является биссектрисой угла правильного шестиугольника.
3. Все углы правильного шестиугольника равны (120^circ).
4. Площадь правильного шестиугольника со стороной (a) равна (dfrac{3sqrt{3}}{2}a^2).
5. Диагонали пересекаются в одной точке и делят его на 6 равносторонних треугольников, у которых высота равна радиусу (r) вписанной в правильный шестиугольник окружности.
6. Инвариантен относительно поворота плоскости на угол, кратный (60^circ) относительно центра описанной окружности (слово “инвариантный” означает, что при таких поворотах правильный шестиугольник перейдёт в себя, то есть такие повороты являются его симметриями).
Замечание
В общем случае правильный (n)-угольник инвариантен относительно поворота на угол (dfrac{360^circ}{n}).
Правильный шестиугольник — это многоугольник, состоящий из шести равных сторон и шести равных углов.
Если шесть равносторонних треугольников расположены бок о бок, то образуется правильный шестиугольник. Поэтому площадь правильного шестиугольника равна шести равносторонним треугольникам.
- Правильный шестиугольник имеет (6) сторон, (6) углов и 6 вершин.
- Сумма внутренних углов шестиугольника (-(6 − 2) · 180° = 720°).
- Внутренний угол правильного шестиугольника равен (720º / 6 = 120º).
- Центральный угол правильного шестиугольника меры: (360 : 6 = 60º).
- Количество диагоналей (- 6 · (6 − 3) : 2 = 9).
- Апофема правильного шестиугольника:
(a=sqrt{l^2-frac{l}{2}})
Свойства правильного шестиугольника
Вот некоторые свойства правильного шестиугольника:
-
Равные стороны: Все стороны правильного шестиугольника имеют одинаковую длину. Это означает, что каждая сторона равна другим сторонам в шестиугольнике.
-
Равные углы: Углы в правильном шестиугольнике равны между собой. Каждый угол равен 120 градусам.
-
Сумма углов: Сумма всех углов в правильном шестиугольнике равна 720 градусам. Это можно получить, умножив число углов (6) на величину каждого угла (120 градусов).
-
Центральная симметрия: У правильного шестиугольника есть центр симметрии, что означает, что при вращении шестиугольника вокруг этого центра на угол 60 градусов он будет выглядеть так же, как и до вращения.
-
Радиус окружности: В правильном шестиугольнике можно описать окружность, в которую все вершины шестиугольника попадают на окружность. Радиус этой окружности может быть найден с использованием формулы: радиус = сторона / (√3), где сторона — длина стороны шестиугольника.
-
Площадь: Площадь правильного шестиугольника может быть вычислена с помощью формулы: площадь = (3√3/2) * сторона^2, где сторона — длина стороны шестиугольника.
Эти свойства помогают определить и описать основные характеристики и свойства правильного шестиугольника.
Часто задаваемые вопросы:
✅ Можно ли вписать правильный шестиугольник в окружность?
↪ Да, правильный шестиугольник можно вписать в окружность таким образом, чтобы все его вершины лежали на окружности.
✅ Какие свойства имеют стороны в правильном шестиугольнике?
↪ В правильном шестиугольнике все стороны равны между собой.
✅ Какова сумма углов в правильном шестиугольнике?
↪ Сумма всех углов в правильном шестиугольнике равна 720 градусов.
Больше уроков и заданий по всем школьным предметам в онлайн-школе «Альфа». Запишитесь на пробное занятие прямо сейчас!
Запишитесь на бесплатное тестирование знаний!
Шестиугольник, виды, свойства и формулы.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник, выпуклый и невыпуклый шестиугольник
Правильный шестиугольник (понятие и определение)
Свойства правильного шестиугольника
Формулы правильного шестиугольника
Правильный шестиугольник в природе, технике и культуре
Звездчатый шестиугольник
Восьмиугольник
Шестиугольник, выпуклый и невыпуклый шестиугольник:
Шестиугольник – это многоугольник с шестью углами.
Шестиугольник – это многоугольник, общее количество углов (вершин) которого равно шести.
Шестиугольник может быть выпуклым и невыпуклым.
Выпуклым многоугольником называется многоугольник, все точки которого лежат по одну сторону от любой прямой, проходящей через две его соседние вершины. Невыпуклыми являются все остальные многоугольники.
Соответственно выпуклый шестиугольник – это шестиугольник, у которого все его точки лежат по одну сторону от любой прямой, проходящей через две его соседние вершины.
Рис. 1. Выпуклый шестиугольник

Сумма внутренних углов любого выпуклого шестиугольника равна 720°.

Правильный шестиугольник (понятие и определение):
Правильный шестиугольник (гексагон) – это правильный многоугольник с шестью сторонами.
В свою очередь правильный многоугольник – это многоугольник, у которого все стороны и углы одинаковые.
Правильный шестиугольник – это шестиугольник, у которого все стороны равны, а все внутренние углы равны 120°.
Рис. 3. Правильный шестиугольник
Правильный шестиугольник имеет 6 сторон, 6 углов и 6 вершин.
Углы правильного шестиугольника образуют шесть равносторонних треугольников.
Правильный шестиугольник можно построить с помощью циркуля и линейки.
Свойства правильного шестиугольника:
1. Все стороны правильного шестиугольника равны между собой.
a1 = a2 = a3 = a4= a5 = a6.
2. Все углы равны между собой и составляют 120°.
α1 = α2 = α3 = α4 = α5 = α6 = 120°.
Рис. 4. Правильный шестиугольник
3. Сумма внутренних углов любого правильного шестиугольника равна 720°.
4. Все биссектрисы углов между сторонами равны и проходят через центр правильного шестиугольника O.
Рис. 5. Правильный шестиугольник
5. Количество диагоналей правильного шестиугольника равно 9.
Рис. 6. Правильный шестиугольник
6. Центр вписанной окружности O1 совпадает с центром описанной окружности O2, что и образуют центр многоугольника O.
Рис. 7. Правильный шестиугольник
7. Правильные шестиугольники замощают плоскость (то есть могут заполнять плоскость без пробелов и наложений).
8. Радиус описанной окружности правильного шестиугольника и его сторона равны.
Рис. 8. Правильный шестиугольник
R = a
Правильный шестиугольник в природе, технике и культуре:
Пчелиные соты имеют форму правильного шестиугольника.
Графит, графен имеют гексагональную кристаллическую решетку.
Гигантский гексагон – атмосферное явление на Сатурне – имеет форму правильного шестиугольника.
Рис. 9. Гигантский гексагон на Сатурне
Сечение гайки и многих карандашей имеет вид правильного шестиугольника.
Игровое поле гексагональных шахмат составляют шестиугольники, в отличие от квадратов традиционной шахматной доски.
Панцирь черепахи состоит из шестиугольников.
Гексагоном иногда называют материковую часть Франции, потому что её географические очертания напоминают данную геометрическую фигуру.
Рис. 10. Материковая часть Франции
Формулы правильного шестиугольника:
Пусть a – сторона шестиугольника, r – радиус окружности, вписанной в шестиугольник, R – радиус описанной окружности шестиугольника, P – периметр шестиугольника, S – площадь шестиугольника.
Формулы периметра правильного шестиугольника:
Формулы площади правильного шестиугольника:
Формула радиуса окружности, вписанной в правильный шестиугольник:
Формула радиуса окружности, описанной вокруг правильного шестиугольника:
R = a
Звездчатый шестиугольник:
Звездчатый шестиугольник (гексаграмма) – это многоугольник, у которого все стороны и углы равны, а вершины совпадают с вершинами правильного многоугольника.
Гексаграмма (др.-греч. ἕξ – «шесть» и γραμμή – «черта, линия») – это звезда с шестью углами, которая образуется из двух наложенных друг на друга равносторонних треугольников.
Прямоугольник
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Шестиугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
7 511
Шестиугольник — это форма с шестью сторонами. Используя правильное уравнение, вы можете найти степень каждого из внутренних углов или углов внутри шестиугольника по углам. Используя другую формулу, вы можете найти внешние углы шестиугольника. Этот процесс, однако, работает только для правильных шестиугольников или тех, в которых все стороны равны. Не существует уравнения для нахождения углов неправильных шестиугольников.
Рассчитайте внутренний угол, умножив 180 (n — 2), где «n» — количество сторон — в данном случае шесть. Умножьте 180 и 4, чтобы получить ответ. Разделите это на число углов, которое составляет шесть. Это даст вам измерение в градусах каждого угла, которое должно быть 120.
Вычислите внешние углы или углы вне шестиугольника, разделив 360 на «n», где «n» равно числу углов. В этом случае вы должны получить 60 градусов.
Проверьте свои ответы, сложив все углы. При сложении всех внешних углов вы должны получить 360 градусов. При сложении всех внутренних углов вы должны получить 720 градусов.
Правильный шестиугольник
Правильный шестиугольник — это такой шестиугольник у которого все шесть сторон равны и его шесть углов равны.
Правильный шестиугольник
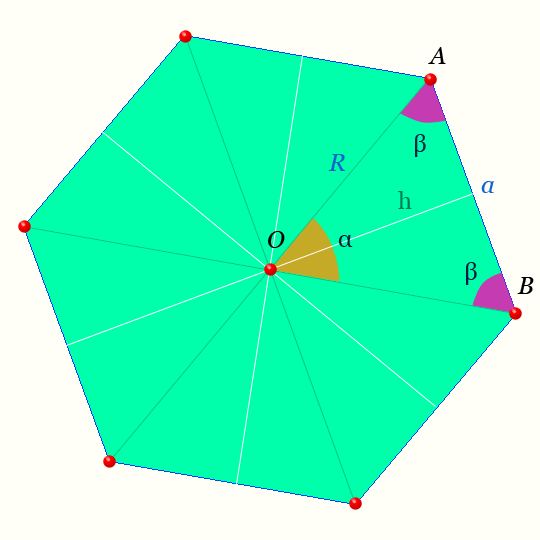
Центр правильного шестиугольника — на рисунке точка O равноудалена от вершин.
Светлая линия обозначающая высоту треугольника AOB : h называется — апофемой.
Отрезки OA, OB — радиусы правильного шестиугольника.
Обозначения на рисунке для правильного шестиугольника
| n=6 | число сторон и вершин правильного шестиугольника, | шт |
|---|---|---|
| α | центральный угол правильного шестиугольника, | радианы, ° |
| β | половина внутреннего угла правильного шестиугольника, | радианы, ° |
| γ | внутренний угол правильного шестиугольника, | радианы, ° |
| a | сторона правильного шестиугольника, | м |
| R | радиусы правильного шестиугольника, | м |
| p | полупериметр правильного шестиугольника, | м |
| L | периметр правильного шестиугольника, | м |
| h | апофемы правильного шестиугольника, | м |
Основные формулы для правильного шестиугольника
Периметр правильного шестиугольника
[ L = 6a ]
Полупериметр правильного шестиугольника
[ p = 3a ]
Центральный угол правильного шестиугольника в радианах
[ α = frac{π}{3} ]
Центральный угол правильного шестиугольника в градусах
[ α = frac{180°}{3} = 60° ]
Половина внутреннего угла правильного шестиугольника в радианах
[ β = frac{π}{3} ]
Половина внутреннего угла правильного шестиугольника в градусах
[ β = frac{180°}{3} = 60° ]
Внутренний угол правильного шестиугольника в радианах
[ γ = 2β = frac{2}{3}π ]
Внутренний угол правильного шестиугольника в градусах
[ γ = frac{2}{3}180° = 120° ]
Площадь правильного шестиугольника
[ S = ph = 3ha ]
Или учитывая формулу Площади правильного шестиугольника получим
[ S = frac{3sqrt{3}}{2}a^2 ]
Отсюда получим апофему правильного шестиугольника
[ h = frac{sqrt{3}}{2}a ]
Правильный шестиугольник |
стр. 270 |
|---|