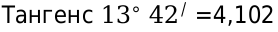Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.
Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:
1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:
Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Тригонометрия в прямоугольном треугольнике
- Тригонометрический круг
- Основное тригонометрическое тождество
- Таблица значений тригонометрических функций
- Градусы и радианы
- Формулы приведения
- Теорема синусов
- Расширенная теорема синусов
- Теорема косинусов
- Тригонометрические уравнения (10-11 класс)
- Примеры решений заданий из ОГЭ
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.

Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник ABC, угол C равен 90°:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x, ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x, против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A. Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B) и на ось игрек (точка C).
Отрезок OB является проекцией отрезка OA на ось x, отрезок OC является проекцией отрезка OA на ось y.
Рассмотрим прямоугольный треугольник AOB:
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y. Точка B в этом случае будет иметь отрицательную координату по оси x. Косинус тупого угла отрицательный.
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x. (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y.
Координата по оси x – косинус угла, координата по оси y – синус угла.
Пример:
cos 150 ° = − 3 2
sin 150 ° = 1 2
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный.
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
| 0° | 30° | 45° | 60° | 90° | |
| sinα | 0 | 12 | 22 | 32 | 1 |
| cosα | 1 | 32 | 22 | 12 | 0 |
| tgα | 0 | 33 | 1 | 3 | нет |
| ctgα | нет | 3 | 1 | 33 | 0 |
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β:
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Скачать домашнее задание к уроку 1.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Что такое синус, косинус, тангенс, котангенс
18 мая 2022
Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
Содержание:
- Ключевые определения: синус, косинус, тангенс, котангенс.
- Почему эти значения зависят только от углов?
- Стандартные углы: 30°, 45°, 60°.
- Простейшие свойства синуса, косинуса, тангенса, котангенса.
- Тригонометрия на координатной сетке.
Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
1. Ключевые определения
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Мы видим, что острый угол $alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $alpha $, назовём противолежащим:
Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.
1.1. Синус, косинус, тангенс, котангенс
Итак, пусть дан прямоугольный треугольник с острым углом $alpha $.
Тогда:
Определение 1. Синус угла $alpha $ — это отношение противолежащего катета к гипотенузе:
[sin alpha =frac{text{противолежащий катет}}{text{гипотенуза}}=frac{a}{c}]
Определение 2. Косинус угла $alpha $ — это отношение прилежащего катета к гипотенузе:
[cos alpha =frac{text{прилежащий катет}}{text{гипотенуза}}=frac{b}{c}]
Определение 3. Тангенс угла $alpha $ — это отношение противолежащего катета к прилежащему:
[operatorname{tg}alpha =frac{text{противолежащий катет}}{text{прилежащий катет}}=frac{a}{b}]
Определение 3. Котангенс угла $alpha $ — это отношение прилежащего катета к противолежащему:
[operatorname{ctg}alpha =frac{text{прилежащий катет}}{text{противолежащий катет}}=frac{b}{a}]
Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).
Рассмотрим пару примеров.
Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.
Имеем:
[begin{align}sin alpha& =frac{BC}{AC}=frac{5}{4} \ cos alpha& =frac{AB}{AC}=frac{3}{5} \ operatorname{tg}alpha& =frac{BC}{AB}=frac{4}{3} end{align}]
Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.
Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:
[operatorname{ctg}alpha =frac{1}{operatorname{tg}alpha }]
Но об этом чуть позже.
Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Это равнобедренный прямоугольный треугольник с катетами $AB=BC=1$. Найдём гипотенузу по теореме Пифагора:
[begin{align}{{ AC}^{2}} & ={{AB}^{2}}+{{BC}^{2}}=1+1=2 \ AC & =sqrt{2} \ end{align}]
Теперь найдём синус, косинус и тангенс:
[begin{align}sin alpha &=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos alpha &=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}alpha&=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)
1.2. Задачи для тренировки
Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.
Задача 3. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{5}{13} \ cos alpha &=frac{12}{13} \ operatorname{tg}alpha &=frac{5}{12} \ end{align}]
Задача 4. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{8}{17} \ cos alpha &=frac{15}{17} \ operatorname{tg}alpha &=frac{8}{15} \ end{align}]
Задача 5. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}}&={{3}^{2}}-{{1}^{2}}=9-1=8 \ l&=sqrt{8}=2sqrt{2} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{3} \ cos alpha&=frac{2sqrt{2}}{3} \ operatorname{tg}alpha&=frac{1}{2sqrt{2}}=frac{sqrt{2}}{4} \ end{align}]
Задача 6. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}} &={{2}^{2}}-{{1}^{2}}=4-1=3 \ l &=sqrt{3} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{2} \ cos alpha&=frac{sqrt{3}}{2} \ operatorname{tg}alpha&=frac{1}{sqrt{3}}=frac{sqrt{3}}{3} \ end{align}]
Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?
2. Теорема о единственности
Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.
Такого не произойдёт. Потому что есть теорема о единственности.
2.1. Формулировка теоремы
Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.
2.2. Доказательство
Рассмотрим произвольный острый угол $alpha $. Для удобства обозначим его вершину буквой $A$:
А затем впишем в него два произвольных прямоугольных треугольника — $ABC$ и $AMN$. Любым удобным способом. Например, можно вписать эти треугольники вот так:
А можно и вот так — это не имеет никакого значения:
Рассмотрим треугольники $ABC$ и $AMN$. Угол $A$ у них общий; углы [angle ABC=angle AMN=90{}^circ ] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
[Delta ABCsim Delta AMN]
Из подобия треугольников следует двойное равенство
[frac{AB}{AM}=frac{BC}{MN}=frac{AC}{AN}]
Выпишем второе равенство — получим пропорцию
[frac{BC}{MN}=frac{AC}{AN}]
Попробуем выразить $sin alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому
[BCcdot AN=MNcdot AC]
Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:
[begin{align}frac{BCcdot AN}{ANcdot AC} &=frac{MNcdot AC}{ANcdot AC} \ frac{BC}{AC} &=frac{MN}{AN} end{align}]
Однако по определению синуса имеем:
[begin{align}sin BAC &=frac{BC}{AC} \ sin MAN &=frac{MN}{AN} \ end{align}]
Получается, что $sin BAC=sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $alpha $ мы всегда будем получать одно и то же значение $sin alpha $.
То же самое касается и $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ — они зависят лишь от градусной меры угла $alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.
3. Стандартные углы
Итак, значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ однозначно определяются величиной угла $alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $alpha $ нельзя найти точные значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
- Верно и обратное: для большинства «красивых» $sin alpha $, $cos alpha $ и т.д. нельзя подобрать подходящий угол $alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
[begin{array}{c|ccc} alpha& 30{}^circ& 45{}^circ & 60{}^circ \ hlinesin alpha & frac{1}{2} & frac{sqrt{2}}{2} & frac{sqrt{3}}{2} \ cos alpha & frac{sqrt{3}}{2} & frac{sqrt{2}}{2} & frac{1}{2} \ operatorname{tg}alpha& frac{sqrt{3}}{3} & 1 & sqrt{3} \ end{array}]
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $alpha =45{}^circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $angle A=angle B=45{}^circ $, получим:
[begin{align}sin 45{}^circ &=sin A=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos 45{}^circ &=sin A=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}45{}^circ&=sin A=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $alpha =30{}^circ $ и $alpha =60{}^circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $angle ABH=angle CBH=30{}^circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
[begin{align} sin{60}^circ &=sin A=frac{BH}{AB}=frac{sqrt{3}}{2} \ cos{60}^circ&=cos A=frac{AH}{AB}=frac{1}{2} \ operatorname{tg}{60}^circ&=operatorname{tg}A=frac{BH}{AH}=sqrt{3} \ end{align}]
И с углом 30°:
[begin{align} sin{30}^circ &=sin ABH=frac{AH}{AB} =frac{1}{2} \ cos{30}^circ &=cos ABH=frac{BH}{AB} =frac{sqrt{3}}{2} \ operatorname{tg}{30}^circ &=operatorname{tg} ABH=frac{AH}{BH} =frac{1}{sqrt{3}} =frac{sqrt{3}}{3} \ end{align}]
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $sin {50}^circ $? Или, быть может, $cos {10}^circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $alpha $:
[sin alpha =sin A=frac{BC}{AB}=frac{3}{5}=0,6]
Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $alpha $, чтобы $sin alpha =0,6$? Сколько градусов должно быть в угле $alpha $? Ответ: неизвестно.:)
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $alpha $, чтобы $sin alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
Мы можем посчитать лишь синус, косинус и тангенс для трёх табличных углов.
Например, $sin 30{}^circ $, $cos 45{}^circ $, $operatorname{tg}60{}^circ $ и т.д. А всякие $sin 15{}^circ $, $cos 25{}^circ $ или $operatorname{tg}89,5{}^circ $ — не сможем. По крайней мере пока.:)
И наоборот:
Зная $sin alpha $, $cos alpha $ или $operatorname{tg}alpha $, мы сможем назвать точный угол $alpha $ только в том случае, если все эти синусы, косинусы и тангенсы — среди табличных значений.
Например, мы точно знаем, что если $sin alpha =frac{sqrt{2}}{2}$, то $alpha =45{}^circ $. Но когда $sin alpha =0,6$, мы уже не можем назвать угол $alpha $ (хотя всегда можем построить такой угол).
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
4. Свойства синуса, косинуса, тангенса
Мы разберём три ключевых свойства:
- Связь между синусом, косинусом и тангенсом.
- Связь между острыми углами прямоугольного треугольника.
- Основное тригонометрическое тождество.
Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.
4.1. Связь между синусом, косинусом и тангенсом
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Выразим синус, косинус:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
А теперь выразим тангенс и заметим, что
[operatorname{tg}alpha =frac{a}{b}=frac{a}{c}cdot frac{c}{b}=frac{sin alpha }{cos alpha }]
Точно так же можно выразить и котангенс:
[operatorname{ctg}alpha =frac{b}{a}=frac{b}{c}cdot frac{c}{a}=frac{cos alpha }{sin alpha }]
Более того, сам тангенс и котангенс тоже связаны:
[operatorname{tg}alpha cdot operatorname{ctg}alpha =frac{a}{b}cdot frac{b}{a}=1]
Мы получили три важнейших тригонометрических формулы:
Основные формулы тригонометрии:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha };quad operatorname{ctg}alpha =frac{cos alpha }{sin alpha };quad operatorname{tg}alpha cdot operatorname{ctg}alpha =1]
Эти формулы нужно знать наизусть. И понимать, откуда они берутся.
4.2. Связь между острыми углами
Рассмотрим прямоугольный треугольник $ABC$, где $angle C=90{}^circ $. Пусть градусная мера $angle A=alpha $ градусов:
Мы помним, что сумма острых углов прямоугольного треугольника равна 90°. Поэтому если $angle A=alpha $, то угол $angle B=90{}^circ -alpha $. Но тогда:
[sin alpha =sin A=frac{BC}{AB}=cos B=cos left( 90{}^circ -alpha right)]
То же самое и с косинусами:
[cos alpha =cos A=frac{AC}{AB}=sin B=sin left( 90{}^circ -alpha right)]
И даже с тангенсами и котангенсами:
[begin{align} operatorname{tg}alpha&=operatorname{tg}A=frac{BC}{AC} =operatorname{ctg}B=operatorname{ctg}left( {90}^circ -alpharight) \ operatorname{ctg}alpha&=operatorname{ctg}A=frac{AC}{BC} = operatorname{tg}B=tgleft( {90}^circ -alpha right) \ end{align}]
Другими словами, если вместо $alpha $ поставить ${90}^circ -alpha $, то исходная тригонометрическая функция поменяется на ко-функцию:
[begin{align}sin left( {90}^circ-alpharight) &=cos alpha \ cos left( {90}^circ-alpharight) &=sin alpha \ operatorname{tg}left( {90}^circ-alpharight) &=operatorname{ctg}alpha\ operatorname{ctg}left( {90}^circ-alpharight) &=operatorname{tg}alphaend{align}]
Но это ещё не всё. Есть гораздо более интересная формула.
4.3. Основное тригонометрическое тождество
Вновь рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Запишем выражения для $sin alpha $ и $cos alpha $:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
Далее заметим, что
[begin{align} {{sin }^{2}}alpha +{{cos }^{2}}alpha&={{left( frac{a}{c} right)}^{2}}+{{left( frac{b}{c} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{c}^{2}}} +frac{{{b}^{2}}}{{{c}^{2}}}= \ & =frac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}} end{align}]
В числителе можем применить теорему Пифагора: ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$, поэтому
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =frac{{{c}^{2}}}{{{c}^{2}}}=1]
Правая часть этой формулы вообще не зависит от угла $alpha $.
Основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Это равенство связывает синус и косинус одного и того же угла и верно для всех $alpha $.
С помощью основного тригонометрического тождества можно вычислять косинус, зная синус, и наоборот.
Задача 7. Найдите $18cos alpha $ для острого угла $alpha $, если $sin alpha =frac{sqrt{65}}{9}$.
Решение. Запишем основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Подставим указанное значение $sin alpha $ и выразим $cos alpha $:
[begin{align}{{left( frac{sqrt{65}}{9} right)}^{2}}+{{cos }^{2}}alpha &=1 \ frac{65}{81}+{{cos }^{2}}alpha &=1 \ {{cos }^{2}}alpha &=frac{16}{81} \ cos alpha&=pm frac{4}{9} end{align}]
Поскольку косинус угла в прямоугольном треугольнике не может быть отрицательным, выбираем вариант $cos alpha ={4}/{9};$. Остаётся сделать финальный шаг:
[18cos alpha =18cdot frac{4}{9}=2cdot 4=8]
Вот и всё! Ответ: 8.
В следующем примере мы уже не будем подробно расписывать каждый шаг. Оформим всё так, как надо оформлять на контрольных и экзаменах.
Задача 8. Найдите $48operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{8}{sqrt{113}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-{{left( frac{8}{sqrt{113}} right)}^{2}}= \ & =1-frac{64}{113}=frac{49}{113} \ sin alpha&=pm frac{7}{sqrt{113}} end{align}]
Но ${0}^circ lt alpha lt {90}^circ $, поэтому $sin alpha gt 0$. Следовательно
[sin alpha =frac{7}{sqrt{113}}]
Найдём $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{7}{sqrt{113}}cdot frac{sqrt{113}}{8}=frac{7}{8}]
Окончательный ответ:
[48operatorname{tg}alpha =48cdot frac{7}{8}=6cdot 7=42]
Ответ: 42.
Заметка на будущее: замечание о том, что угол $alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.
Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.
Но всё это будет чуть позже. А сейчас потренируемся.
Задача 9. ►
Найдите $52cos alpha $ для острого угла $alpha $, если $sin alpha =frac{5}{13}$.
Решение. Найдём $cos alpha $:
[begin{align}{{cos }^{2}}alpha &=1-{{sin }^{2}}alpha = \ &=1-frac{25}{169}=frac{144}{169} \ cos alpha&=pm frac{12}{13} end{align}]
Поскольку $cos alpha gt 0$ для острых $alpha $, выбираем $cos alpha ={12}/{13};$. Итого
[52cos alpha =52cdot frac{12}{13}=48]
Ответ: 48.
Задача 10. ►
Найдите $1+2operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{1}{sqrt{26}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-frac{1}{26}=frac{25}{26} \ sin alpha&=pm frac{5}{sqrt{26}} end{align}]
Поскольку $sin alpha gt 0$ для острых $alpha $, выбираем
[sin alpha =frac{5}{sqrt{26}}]
Считаем $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{5}{sqrt{26}}cdot frac{sqrt{26}}{1}=5]
Откуда
[1+2operatorname{tg}alpha =1+2cdot 5=11]
Ответ: 11.
5. Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Задача 11. Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение. Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ на луч $BC$.
Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{3}{4}=0,75]
Это и есть искомый тангенс.
Ответ: 0,75.
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:
Задача 12. ►
Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение.
Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ к лучу $BC$.
Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{2}{4}=frac{1}{2}]
Ответ: 0,5.
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.
Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:
Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.
Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.
Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.
Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:
[operatorname{tg}MNK=frac{HK}{HN}=frac{sqrt{2}}{2sqrt{2}}=frac{1}{2}=0,5]
Здесь мы предположили, что сторона квадрата сетки равна 1. Но с тем же успехом можно считать, что сторона квадрата $a$:
[operatorname{tg}MNK=frac{HK}{HN}=frac{asqrt{2}}{2asqrt{2}}=frac{1}{2}=0,5]
Ответ: 0,5.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Задача 14. ►
Найдите тангенс угла $DEF$, изображённого на координатной сетке:
Решение.
Дополнительное построение: отрезок $DH$.
Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $operatorname{tg}DEF=1$.
Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:
[operatorname{tg}DEF=frac{asqrt{10}}{asqrt{10}}=1]
Ответ: 1.
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.
К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
Смотрите также:
- Радианная и градусная мера угла
- Как быстро запомнить таблицу синусов и косинусов
- Сложные логарифмические неравенства
- Сложные выражения с дробями. Порядок действий
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2
В статье мы расскажем, как находить значения:
(cos300^°), (sin(-540^°)), (cos 510^°), (sin(-135^°))
и других тригонометрических выражений без тригонометрической таблицы.
Как вычисляются синусы и косинусы углов?
Чтобы вычислить косинус и синус некоторого угла нужно:
1. Отложить этот угол на тригонометрическом круге и определить какая точка соответствует этому углу;
2. Найти абсциссу и ординату этой точки. Косинус угла равен — абсциссе, а синус угла — ординате.
Предположим, стоит задача найти косинус и синус угла (30^°). Отложим на круге угол в (30^°) и найдем какая точка соответствует этому углу.
Если построить все точно, то видно, что абсцисса точки равна (0,866)… , что равно числу (frac{sqrt{3}}{2}) , а ордината равна (0,5), то есть (frac{1}{2}).

Получается, (cos 30^° = frac{sqrt{3}}{2}), а (sin30^° =frac{1}{2}).
Аналогично и для любой другой точки на круге: значение абсциссы равно косинусу угла, а ординаты – синусу угла. Поэтому:
В тригонометрии ось абсцисс (ось x) часто называют «ось косинусов», а ординат (ось y) – «ось синусов».
Обычно на осях не отмечают (0,1); (0,2); (0,3) и т.д., а сразу наносят стандартные значения для синуса и косинуса: (±frac{1}{2}=±0,5); (±frac{sqrt{2}}{2} ≈±0,707); (±frac{sqrt{3}}{2} ≈±0,866).
Первый шаг к тому, чтобы находить синусы и косинусы стандартных углов – научится отмечать эти углы на тригонометрическом круге.
Как отметить любой угол на тригонометрическом круге?
Для этого нужно знать несколько фактов:
- Начало отсчета находится в крайней правой точке окружности;
-
Чтоб отложить положительный угол нужно двигаться против часовой стрелки от начала отсчета, чтобы отметить отрицательный – по часовой стрелке;
-
Градусная мера окружности равна (360^°), полуокружности (180^°), а четверти (90^°);
-
Углы в (0^°), (30^°), (45^°) и (60^°) выглядят так:


- Одна точка может соответствовать разным углам;
- Угол может быть больше (360^°). В этом случае он просто сделает полный оборот и пойдет дальше. Фактически, можно (360^°) просто отбросить и откладывать тот угол, который останется – в итоге вы всё равно окажетесь в той же точке.
Пример. Отметьте угол в (90^° ) и (-90^°).
Решение:

Пример. Отметьте угол в (225^° ) и (-135^°).
Решение: (225^°=180^°+45^°)
(-135^°=-90^°-45^°)

Пример. Отметьте угол в (420^° ) и (-390^°).
Решение: (420^°=360^°+60^°)
(-390^°=-360^°-30^°)


Задание 1. Отметьте на окружности точки соответствующие углам: (720^°), (225^°), (300^°), (870^°), (900^°), (-330^°), (-630^°), (-210^°).
Как находить синус и косинус любого угла?
Простой алгоритм:
- Начертите тригонометрический круг и оси косинусов и синусов (не обязательно рисовать прям аккуратно, как на картинке ниже, можно и некрасиво – главное не запутаться какая точка к какому значению относится).
- Отложите на круге угол, синус и косинус которого надо найти, и определите точку на круге, соответствующую этому углу.
- Найдите координаты точки, используя картинку ниже.

Пример. Вычислите (sin300^°) и (cos300^°) .
Решение: (300^°=360^°-60^°)

(cos 300^°=frac{1}{2}), (sin{300^°}=-frac{sqrt{3}}{2}).
Пример . Вычислите (sin(-540^°)) и (cos(-540^°)) .
Решение. (-540^°=-360^°-180^°).

(-540^°) на тригонометрическом круге совпадает с (-1) на оси косинусов. То есть, координаты этой точки: ((-1;0)). Значит, (cos(-540^°)=-1), а (sin(-540^° )=0).
Да, имея перед глазами тригонометрический круг, вычислять синусы и косинусы любых углов легко. Возможно, у вас возник вопрос: «а что делать, если круга нет? Как делать такие вычисления на ЕГЭ?». Ответ очевиден – нарисовать круг самому! Для этого надо понять, как располагаются значения на нем. Подробную методику того, как это делается я рассказывала в этой статье.
Есть и другой способ запомнить тригонометрический круг – внимательно посмотреть на картинку ниже и запомнить максимальное количество элементов. После прикройте страницу и по памяти нарисуйте круг и отметьте всё, что смогли запомнить. Сверьте, что у вас получилось с тем, что было на картинке. Повторяйте эту последовательность действий пока по памяти не получится нарисовать тригонометрический круг со всеми значениями. Это займет 15 минут вашего времени, но сильно поможет в 13 задаче ЕГЭ (и не только в ней).

Примеры вычисления синуса и косинуса из ЕГЭ
В двух следующих примерах я специально рисовала круг от руки, чтобы вы увидели, как выглядят реальные решения.
Пример . Найдите значение выражения (-18sqrt{2}sin(-135^°)).
Решение. (-135^°=-90^°-45^°)

Получается (-18sqrt{2} sin(-135^° )=-18sqrt{2}cdot-frac{sqrt{2}}{2}=frac{18cdotsqrt{2}cdotsqrt{2}}{2}=9cdot 2=18.)
Ответ: (18).
Пример . Найдите значение выражения (54sqrt{3}cos(510^°)).
Решение. (510^°=360^°+150^°=360^°+180^°-30^°.)

(54sqrt{3}cos(510^°)=54sqrt{3}cdot(-frac{sqrt{3}}{2})=-frac{54cdot sqrt{3}cdot sqrt{3}}{2}=-27cdot 3=-81.)
Ответ: (-81).
Смотрите также:
Как найти тангенс и котангенс без тригонометрической таблицы? Из градусов в радианы и наборот
Тригонометрическая таблица с кругом
Почему в тригонометрической таблице такие числа?
Для тех кто хочет закрепить знания:
Задание на вычисление синусов, косинусов, тангенсов и котангенсов
Определение значения синуса, косинуса, тангенса и котангенса
Определение
Тригонометрия — это техническая часть математики, в которой представлены особенности взаимосвязи между сторонами и углами треугольников.
Тригонометрические функции, является очень важной составляющей не только математики, но других технических наук.
Применяя основные формулы и законы тригонометрии при вычислении задач. Огромное значение имеют таблицы значений данных функций. Они существенно упрощают решение задач различной сложности.
Процесс работы и расчета функций данного вида, очень непростой. Решение задач и уравнение, очень часто вызывают сложности. Поэтому, со временем, были созданы и разработаны несколько видов решений, чтобы облегчить жизнь математика и всем представителям технических наук. Преобразовывая тригонометрические формулы, необходимо руководствоваться следующими правилами:
- Нельзя продумывать весь процесс решения от начала до самого конца сразу. Нужно определиться с основными задачами и данными.
- Весь пример, подвергать упрощению или преобразования постепенно;
- Разрешается применять все преобразования и действия, связанные с алгеброй, а именно: вынести значение за пределы скобок. сократить значение и многое другое:
[
sin x=frac{a}{c} ; cos x=frac{b}{c} ; operatorname{tg} x=frac{sin x}{cos x} ; operatorname{ctg}=frac{1}{operatorname{tg} x}=frac{sin x}{cos x}
]
Зная основные определения тригонометрических функций, можно определить их угловые значения. Для углов от нуля до трехсот шестидесяти градусов, вычислим данные и запишем их в виде таблицы.
Значения вышеупомянутых математических функций, в частности в разделе геометрия, вычисляются как соотношения длин прямоугольного треугольника.
Углы геометрической фигуры имеют соответствующие значения в градусах. Используя основные определения математики, а именно тригонометрии можно определить нужные нам данные.
Определим основные значения
1.синуса (sin):
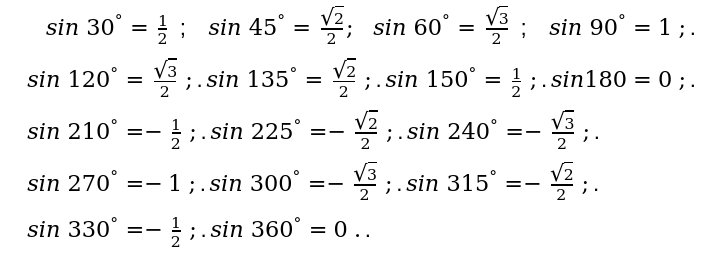
2. косинуса (cos):
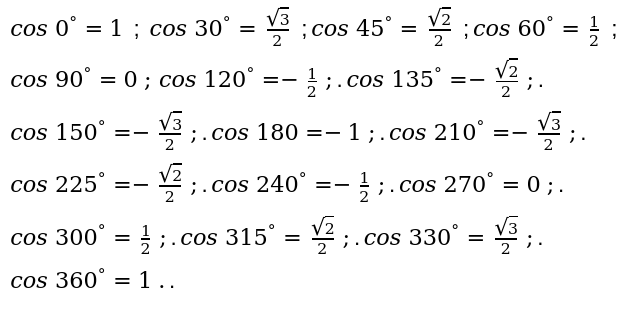
3. тангенса(tg):
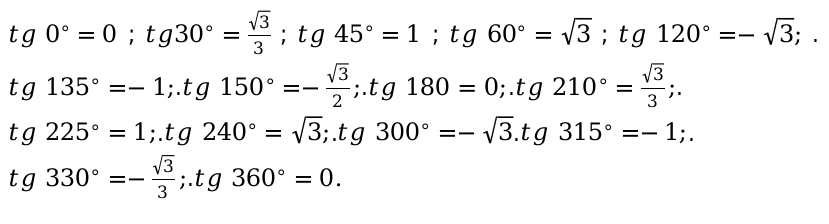
[
operatorname{tg} 90^{circ}, 270^{circ}
]
Данные выше угловые значения, не определяются, согласно основным законам геометрии и математики.
4. котангенса (ctg)
[
operatorname{ctg} 0^{circ}, 180^{circ}, 360^{circ}
]
Для перечисленных выше угловых значений по законам математики и всех технических наук в целом, значения не определяются
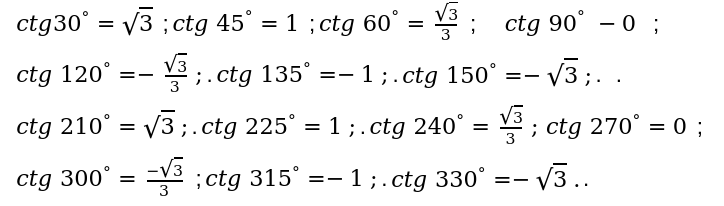
Мы произвели основные расчеты. Определили результаты угловых значений.
Мы определились с основными угловыми значениями функций. Следующим шагом будет их сведение в таблицу.
Таблица1. Основные значения функций косинус, синус, тангенс и котангенс, для угловых значений и радиан
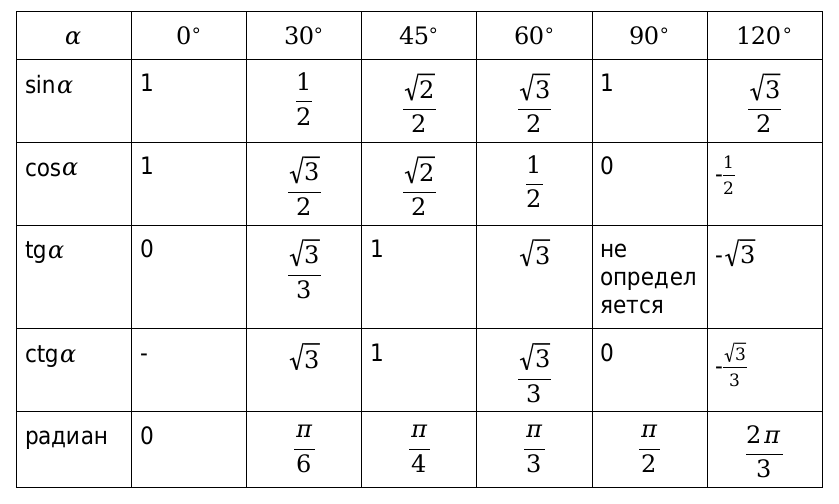
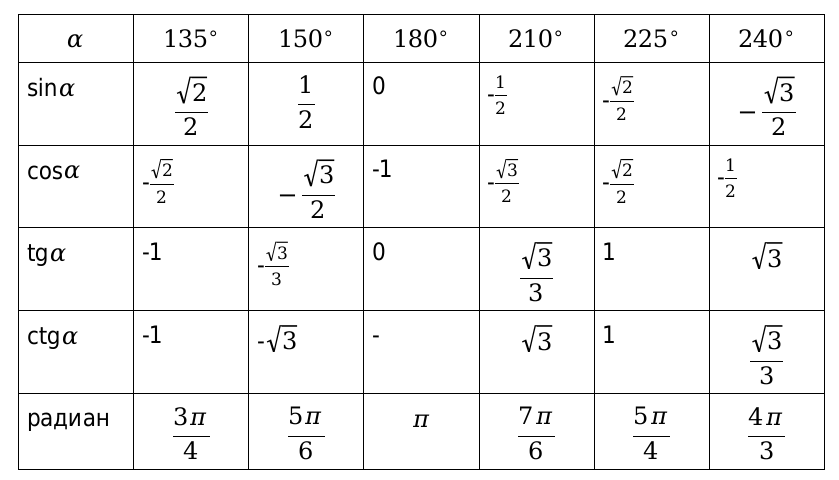
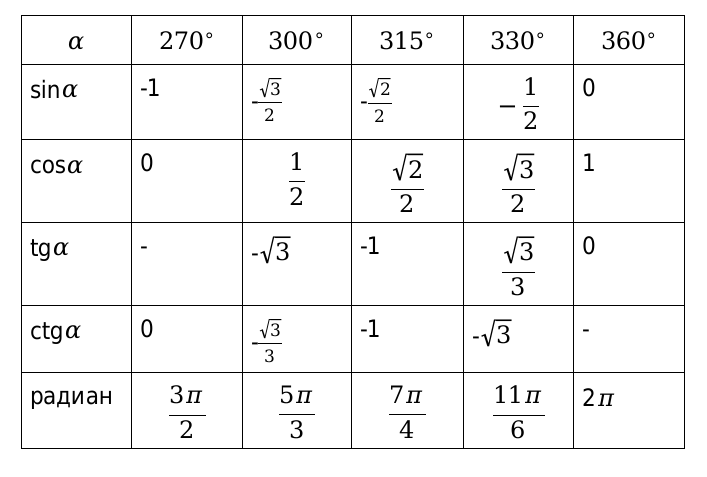
Вычисленные значения принято сводить в таблицу, показанную выше. Особенно рекомендуются, ее заучивать наизусть, для более лучшего восприятия. Рассмотрим, также значения для нестандартных угловых значений и сведем их в таблицу.
Таблица 2. Нестандартные углы функций косинус, синус, тангенс и котангенс в тригонометрии

В данной таблице приведены значения углов, которые считаются нестандартными, также таблица необходима, чтобы облегчить жизнь, в первую очередь, школьной программе.
Например:
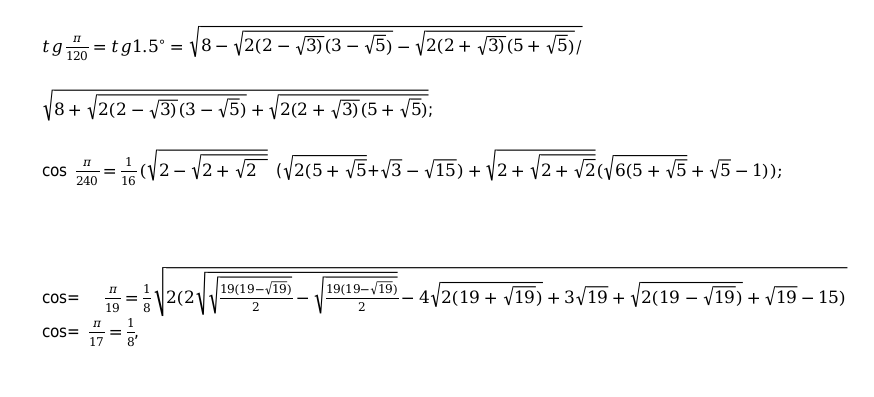
Значение заданной функции берется из таблицы. Оно равняется данному, которое попадает на пересечение столбца и строки.
Пример №1. Необходимо определить чему равен [operatorname{tg} 300]
Берем левый столбец с наименованием функции, находим в верхней строке нужный градус, и на пересечении определяем нужный ответ.
Следовательно:[operatorname{tg} 300^{circ}=-sqrt{3}].
Пример №2. Необходимо определить чему равен [cos frac{5 pi}{3}].
Берем левый столбец с наименованием функции, находим в нижней строке значение радиан, поднимается на верх таблицы и определяем градусы.
[text { Следовательно: } operatorname{tg} 300^{circ}=frac{1}{2} .]
Пример №3. Необходимо определить чему равен [cos frac{11 pi}{6}].
Проводим аналогичные действия, как в предыдущих двух примерах и определяем угловое значение.
[text { Следовательно } cos =frac{sqrt{3}}{2}=330^{circ}.]
Таблица Брадиса для решения основных задач по тригонометрии
Первое упоминание о таблице, датируется 20-ми годами прошлого века. Основоположником, является советский ученый математик, и талантливый педагог Владимир Брадис. Созданная Брадисом таблица, позволяет определить значения тригонометрических функций, с большой точностью, а именно до четырех знаков. На практике решений, обычно требуется точность в три-четыре знака, после запятой, но не более. Для расчета, с такой точностью, значение синуса, в формуле достаточно трех известных слагаемых, а иногда и двух. Произвести простых четыре перемножения. Дважды разделить, умножить и отнять.
Если производить действия инженерным калькулятором, становится понятно, что все вышеперечисленные действия, уже запрограммированы в его микросхеме. В таблице представлены следующие данные:
- число в квадратной и кубической степени;
- числа квадратных корней;
- логарифмические функции и значение;
- функции тригонометрии, представленный в градусах и радианах;
- обратные функции.
Можно определить точность углового значения до минуты. Существуют также таблицы, где есть семизначные значения.
Для того чтобы составить таблицы следует пользовался методом разложения функций (либо метод разложения на степень в ряд)
Примеры решения задач
Пример 1:
Необходимо определить синус угла 18 ° 44 ‘.
По таблице значений определяем данные синуса 18 ° 42 ‘. Далее используем поправку, равную две минуты. Плюсуем ее и заданные минуты: 18 ° 44 ‘ − 18 ° 42 ‘ = 2 ‘
Нужное значение равняется — 0,0006.
Узнав все необходимые значения, находим окончательное решение:
sin 18 ° 44 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 2:
Условие задачи, заключается в необходимости вычислить угол функции синус 76 ° 12. В таблице находим столбец с название угол и ищем 76 градусов и строку со значением 12. Далее, исходя из найденных ячеек, находим значение угла — 0,2284.
Ответ: синус 76 ° 12 =0,2284.
Пример 3:
Нужно найти значение синус 16 градусов 32 минут. Для того чтобы посчитать значение 16 ° 32 минуты. В таблице находим значение нужного угла, которое ближе всего по значению подходит к заданному. Это sin16 30 =0.2840. Так как 16 32=16 30+2, то в столбце, выбираем нужную поправку, которая находится на пересечении со строкой, со значением 16 градусов стоит 0,0006, то есть
sin 16 ° 32 ‘ = 0. 3208 + 0. 0006 = 0. 3214
Пример 4:
Нужно найти значение синус 22 градусов 10 минут. Чтобы посчитать значение 22 ° 12, в таблице найдем значение необходимого угла, наиболее подходящее заданному. Это sin16 30 =0.3778. Так как 22 ° 10= 22 ° 12+2, то тогда выбираем поправку равную двум и видим, что нужный нам градус равный 22 ° имеет значение 0,0005. Далее записываем:
sin 22 ° 10 ‘ = (22 12-2) =0. 3778 + 0. 0005 = 0. 3773
Пример 5:
Нужно найти значение косинус 50 градусов 33 минут. Для того, чтобы посчитать значение 53 31 в таблице найдем значение нужного угла, наиболее близкого к искомому со знаком минус. Это косинус 50 33 =0.6361 Так как 50 33=50 30+3, то в нужном столбце выбираем значение 3. Далее находим значение 0,0007, и записываем следующее уравнение:
косинус 50 ° 33 ‘ = (50 30-3) =0. 6361 +(- 0. 0007) = 0. 6454
Пример 6:
Нужно найти tg 35 градусов 6 минут. В таблице значений функции, в столбце найдем значение 35 градусов, а в строке 6 минут. Определяем нужное значение по таблице равное 0,7028.
Пример 7:
Нужно найти значение котангенс 13 градусов 42 минут. Снова применим таблицу значения функций и найдем значение 13 градусов, а в строке 40 минут и поправку равную 2. Находим искомое значение 4,102.
Пример 8:
Нужно найти значение косинус для 49° 33 минут.
Для того чтобы вычислить значение 49° 31. В таблице найдем значение угла, наиболее близкого по значению к заданному, но только с отрицательным знаком минус. Это косинус 49° 31/ =0.6361 Так как 49° 31/=50 30+3, из этого следует, что поправка равняется трем. Значение 49 градусов равно 0,0007, поэтому: косинус 49° 33 ‘ = ( 49° 31-3) =0 . 6361 +(- 0 . 0007) = 0,6454
Нет времени решать самому?
Наши эксперты помогут!
Основные способы, которые помогут заполнить таблицу функций
1 Действие: Необходимо изобразить простую таблицу, где будет несколько столбцов и строк, необходимых для заполнения данных. Следующая задача, состоит в том, что нужно пустые графы заполнить. Записываем в первом столбике значение математических функций, ранее нами изученных.
В начальной строке, должны отображаться самые часто используемые значения углов: от нуля до девяноста градусов и так далее.
Оставшиеся ячейки нужно оставить незаполненными, для следующих действий. Чтобы понять тригонометрию, нужно изучать не только основные функции. Стоит уделить внимание и таким функциях как: косеканс (cosec) и секанс (sec).
2. Действие: Заполняем пустые ячейки со значение синус. Берем выражение [frac{sqrt{x}}{2}] и подставляем числовые значения, то есть величины углов. они записаны в первом столбике. Далее применяя [frac{sqrt{x}}{2}] можно вычислить данные для углов, которые нам необходимы. Вычисленные значения, записываются в таблицу.
Для наглядности все прописанные действия, можно разобрать на конкретном примере.
Например, мы заполняем ячейку sin 0 градусов. На месте неизвестного значения в выражении [frac{sqrt{x}}{2}] записываем значение угла.
Получаем следующую запись: [frac{sqrt{x}}{2}=frac{0}{2}=0]. Затем, проводим те же операции для заполнения оставшихся пустых строк.
[
frac{sqrt{1}}{2}=frac{1}{2} ; frac{sqrt{2}}{2}=frac{(sqrt{2 cdot 2})}{(2 cdot sqrt{2})}=frac{2}{2 cdot sqrt{2}}=frac{1}{sqrt{2}} ; frac{sqrt{3}}{2} frac{sqrt{4}}{2}=frac{2}{2}=1
]
Необходимо первым делом заполнять неизвестные ячейки, для функции синус. Это значительно в будущем облегчит заполнение всей таблицы. Так как именно за данной функции и ее данных и завязана вся работы таблицы.
3. Действие: Продолжаем считать таблицу. для этого значения синуса, которые подсчитаны были ранее, переписываем для функции косинус. Только делаем это в порядке обратном значению синусу. Данная теория действительна, потому что sin x° = cos (90-x). Если в самой крайней ячейке синус, имеется 1(sin90°=1). То в первую строку значения косинус, перепишется это числовое значение, cos 0° = 1. Таким образом заканчиваем заполнение до конца.
4. Действие: Для определения тангенса. Необходимо произвести деление данных синуса на косинус. Так как тангенс равен данной функции. [operatorname{tg}=frac{sin }{cos }]. Выходим что искомое значение равно данному выражению. Если [operatorname{tg} 45^{circ}=frac{sin }{cos }=frac{sqrt{1}}{2} / frac{sqrt{3}}{2}=frac{1}{sqrt{3}} .]
Аналогично поступаем и далее.
5. Действие: Для заполнения граф косеканс и секанс нужно 1/sin и 1/cos.
[text { Так как, } operatorname{cosec}=frac{1}{sin } . text { Например, } sin 40^{circ}=frac{1}{2}, text { поэтому } operatorname{cosec} 40^{circ}=frac{1}{frac{1}{2}}=2]
Действие 6: Оставшиеся функции тангенс и котангенс. также записываются обратно значениям. Если tg90 равняется ctg0, значение tg60 будет соответственно равен значению ctg 30 градусов.
[text { Таким же методом заполняются оставшиеся строки таблицы. Так } text { как } operatorname{ctg}=frac{1}{t g}, text { в свою очередь } operatorname{ctg}=frac{cos }{sin }]
Вычисление данных при помощи фигуры — прямоугольный треугольник
Для этого строится нужный треугольник заданным углом, который необходимо определить. Строится угол, точка и луч, которые выходят из данной точки под определенным углом. Соединяем лучи, прямой линией перпендикулярной, одному из лучей. В конечном итоге получаем фигуру, угол которой равняется заданному в задаче углу. В процессе вычисления, также задаются длины сторон. Поэтому трудней с построением не должно возникнуть.
Вычисление при помощи длин сторон треугольника происходит следующим образом:
- обозначается катет;
- сторона возле угла;
- сторона напротив угла с прямым значением.
Функции могут выражаться по-разному в отношении сторон. Например, нам нужно определим значение sin 45°. Поделим имеющуюся длину значения противолежащего катета на значение длины гипотенузы. Если заданные значения длины равны 4 и 6 соответственно. Тогда, составим следующее выражение и получим sin[45^{circ}=frac{4}{6}=0,67]
Для определения значений основных функций в математике, необходимо заучить наизусть определение основных понятий, связанный с данной темой.
В процессе решения задачи, это придется применять постоянно.
Значения косеканса и секанса определяются в обратном порядке. Для этого необходимо знать какие стороны нужно делить для определения вышеперечисленных функций.
Косеканс находится [operatorname{cosec}=frac{1}{sin }] следовательно, нужно разделить гипотенузу на противолежащий катет. Секанс, наоборот к прилежащему катету [mathrm{sec}=frac{1}{cos }].
Например, для определения cosec 40°, если катет равен 5, а гипотенуза соответственно равна 8. Нужно разделить 5/8 и получим ответ cosec 40° = 0,63.
При вычислениях всегда рекомендуется исключать значение под корнем в знаменателе, это наиболее облегчает процесс расчета.
Рассмотренная тема преобразования и расчета функций, является довольно громоздкой, на первый взгляд. Применяя для решения огромные формулы и функции можно растеряться и не сразу сообразить, как производить их расчет. Однако досконально рассмотрев и изучив каждый раздел, становится понятно, что все достаточно просто и громоздкие таблицы освоить можно быстро и легко.
Вычисление значений углов по окружности
Самый простой и понятный способ для вычисления углов и радиан.
Для этого вычерчиваем окружность с радиусом R. Он в свою очередь, равен единичному значению. Центр окружности равен центру системы координат. От положительной оси считаем углы, по часовой стрелке, выполняющей движении против хода. Точка, имеющая координаты 1;0 равняется угловому значению ноль. если координаты -1;0, тогда угол равен 90 градусов. Точка, находящаяся на окружности, соответствует углу от нуля до 360 градусов. Так как окружность является единичной, значения углов для синуса и косинуса находятся в пределах от -1 до 1:
Определяются знаки функций, также по окружности. если угловое значение более 360 градусов, делается два оборота по часовой стрелке и плюсуется еще дополнительно 12 минут.
[
cos (alpha+360 cdot n)=sin alpha
;]
[
sin (alpha+360 cdot n)=sin alpha /
]
Значения тангенсов и котангенсов, можно вычислить аналогично, по окружности. Однако легче посчитать по формулам, уже известных данных.
[
operatorname{tg} alpha=frac{sin alpha}{cos alpha} ; operatorname{ctg} alpha=frac{cos alpha}{sin alpha}
]